Seri “Bunyi putih menarik kotak hitam”
Sejarah siklus publikasi ini dimulai dengan fakta bahwa dalam buku
G.Sekey "Paradoks dalam Teori Probabilitas dan Statistik Matematika" (
p. 43 ), pernyataan berikut ditemukan:

Fig. 1.
Menurut analisis, komentar pada publikasi pertama (
bagian 1 ,
bagian 2 ) dan alasan selanjutnya telah mematangkan ide untuk menyajikan teorema ini dalam bentuk yang lebih visual.
Sebagian besar anggota masyarakat mengenal segitiga Pascal, sebagai konsekuensi dari distribusi probabilitas binomial dan banyak hukum terkait. Untuk memahami mekanisme pembentukan segitiga Pascal, kami akan mengembangkannya lebih terinci, dengan penyebaran arus pembentukannya. Dalam segitiga Pascal, node dibentuk oleh rasio 0 dan 1, gambar di bawah ini.
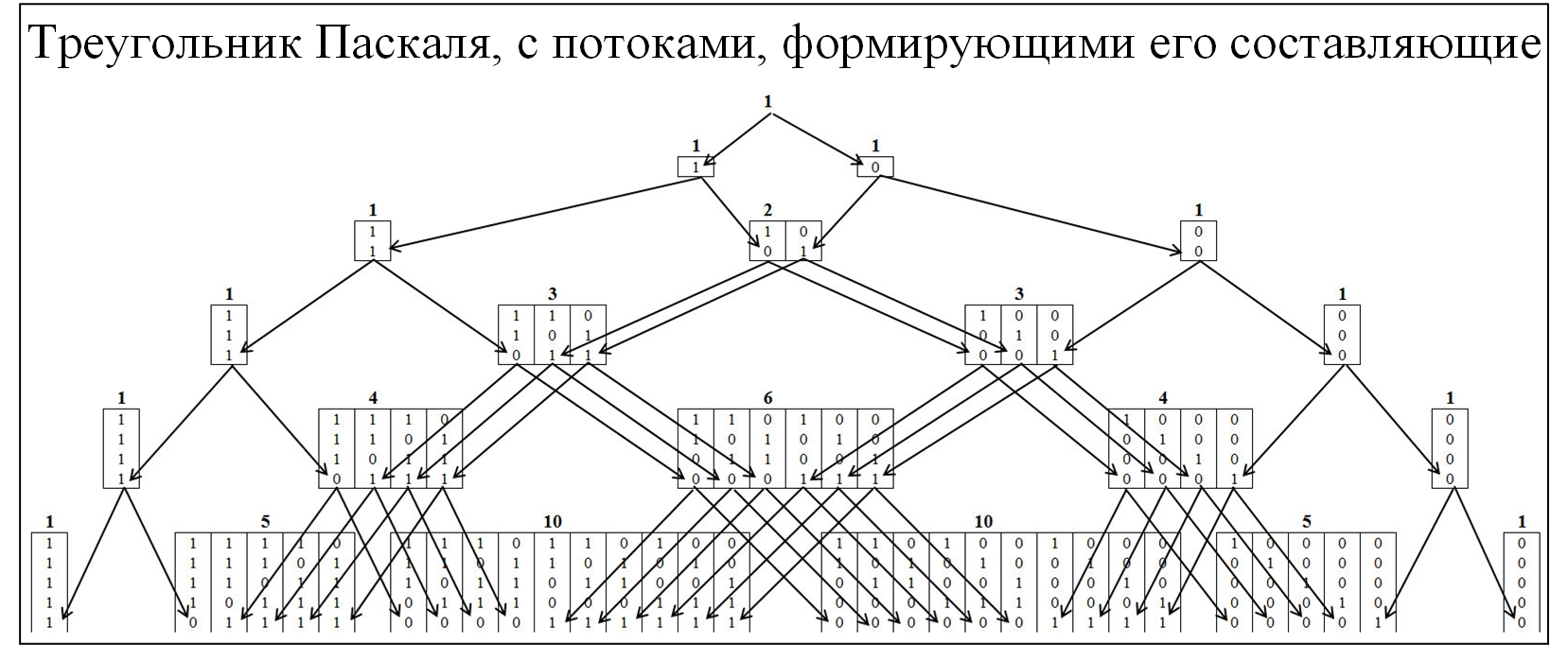
Fig. 2.
Untuk memahami teorema Erds-Renyi, kita akan membuat model yang sama, tetapi node akan dibentuk dari nilai-nilai di mana rantai terbesar hadir, terdiri secara berurutan dari nilai yang sama. Clustering akan dilakukan sesuai dengan aturan berikut: rantai 01/10, untuk cluster "1"; rantai 00/11, untuk mengelompokkan “2”; rantai 000/111, untuk mengelompokkan "3", dll. Dalam hal ini, kita akan memecah piramida menjadi dua komponen simetris Gambar 3.

Fig. 3.
Hal pertama yang menarik perhatian Anda adalah bahwa semua gerakan terjadi dari cluster yang lebih rendah ke yang lebih tinggi dan sebaliknya tidak bisa. Ini wajar, karena jika rantai ukuran j telah terbentuk, maka ia tidak bisa lagi menghilang.
Menentukan algoritma konsentrasi angka, kami berhasil mendapatkan rumus perulangan berikut, mekanisme yang ditunjukkan pada Gambar 4-6.
Nyatakan elemen di mana angka-angka terkonsentrasi. Dimana n adalah jumlah karakter dalam jumlah (jumlah bit), dan panjang rantai maksimum adalah m. Dan setiap elemen akan menerima indeks n; mJ.
Nyatakan bahwa jumlah elemen dilewatkan dari n; mJ ke n + 1; m + 1J, n; mjn + 1; m + 1.

Fig. 4.
Gambar 4 menunjukkan bahwa untuk cluster pertama tidak sulit untuk menentukan nilai setiap baris. Dan ketergantungan ini sama dengan:

Fig. 5.
Kami menentukan untuk cluster kedua, dengan panjang rantai m = 2, Gambar 6.
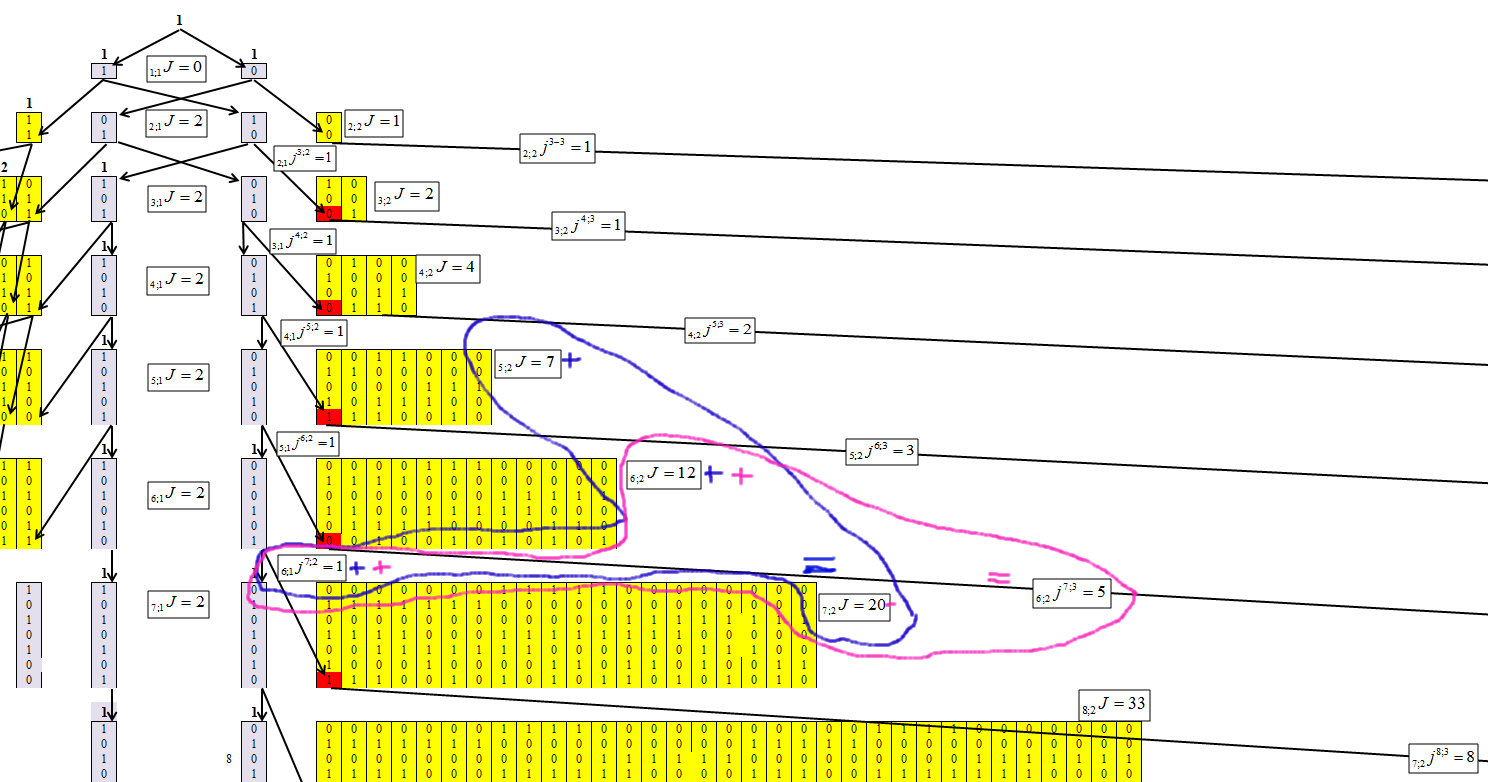
Fig. 6.
Gambar 6 menunjukkan bahwa untuk cluster kedua, ketergantungan sama dengan:

Fig. 7.
Kami menentukan untuk cluster ketiga, dengan panjang rantai m = 3, Gambar 8.
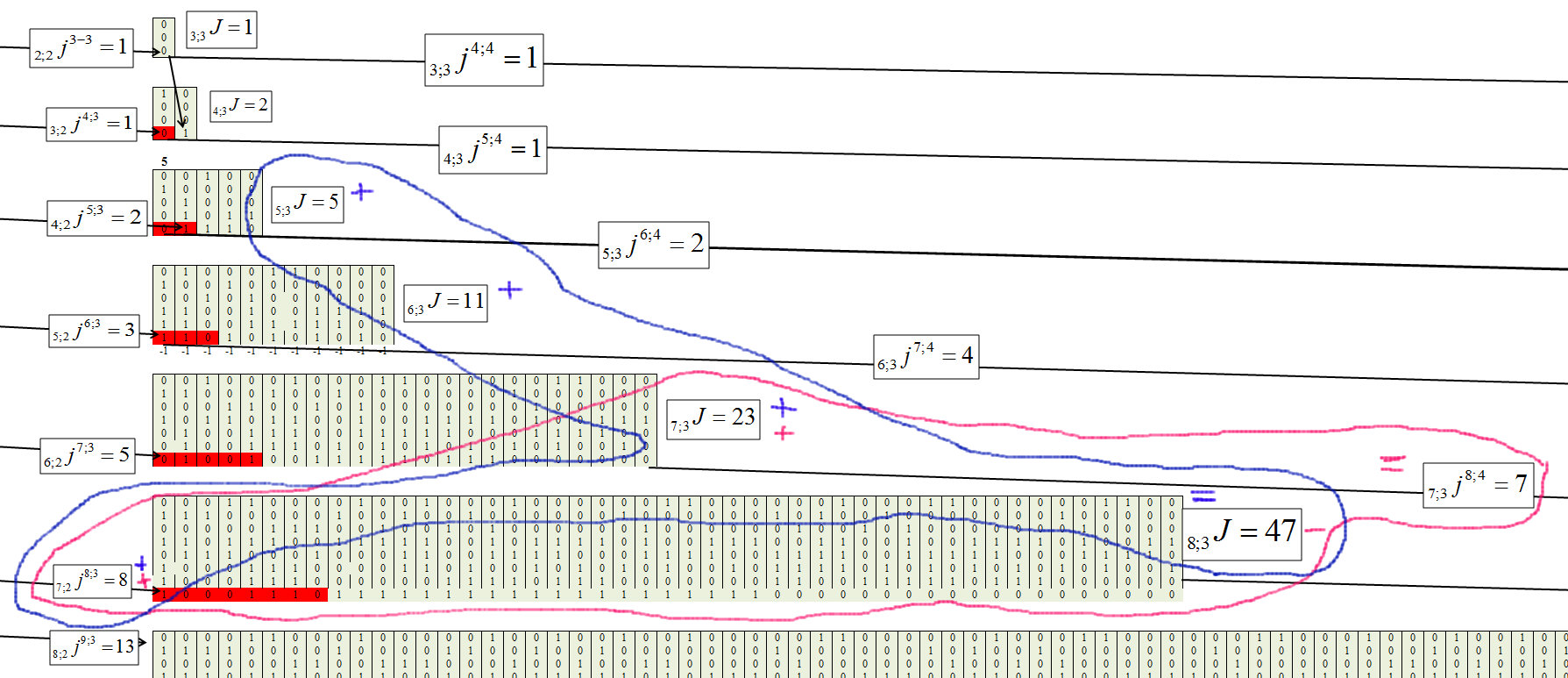
Fig. 8.

Fig. 9.
Rumus umum setiap elemen berbentuk:

Fig. 10.

Fig. 11.
Verifikasi
Untuk verifikasi, kami menggunakan properti dari urutan ini, yang ditunjukkan pada Gambar 12. Terdiri dari fakta bahwa anggota terakhir dari suatu garis dari posisi tertentu mengambil nilai tunggal untuk semua garis dengan bertambahnya panjang garis.
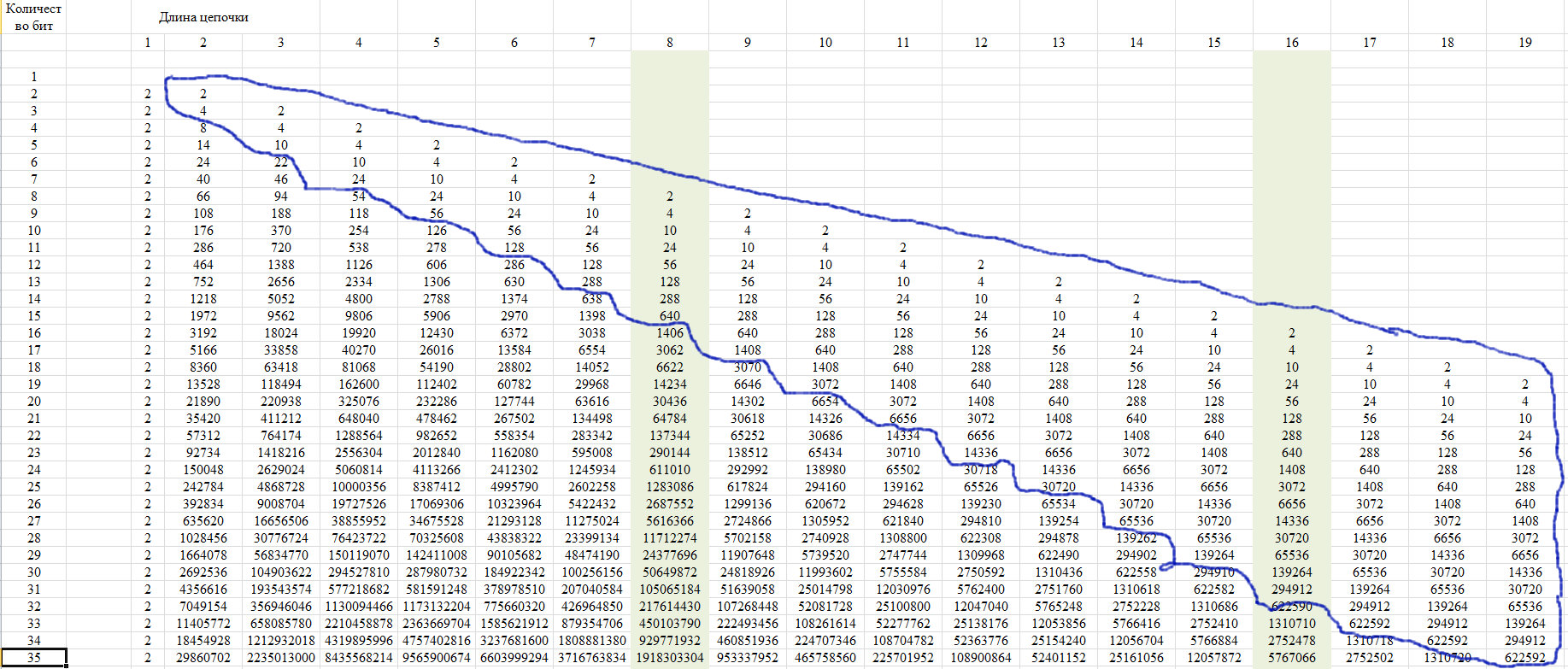
Fig. 12.
Properti ini disebabkan oleh fakta bahwa dengan panjang rantai lebih dari setengah seluruh baris, hanya satu rantai yang mungkin. Kami menunjukkan ini dalam diagram pada Gambar 13.

Fig. 13.
Dengan demikian, untuk nilai k <n-2, kami memperoleh rumus:
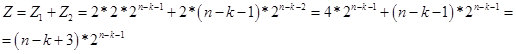
Fig. 14.
Bahkan, nilai Z adalah jumlah potensial angka (opsi dalam string n bit) yang berisi rantai elemen k identik. Dan menurut rumus perulangan, kami menentukan jumlah angka (opsi dalam string n bit) di mana rantai k elemen identik adalah yang terbesar. Untuk saat ini, saya berasumsi bahwa nilai Z adalah virtual. Oleh karena itu, di wilayah n / 2, ia masuk ke ruang nyata. Pada Gambar 15, layar dengan perhitungan.

Fig. 15.
Mari kita tunjukkan contoh kata 256-bit, yang dapat ditentukan oleh algoritma ini.

Fig. 16.
Jika ditentukan oleh standar keandalan 99,9% untuk GSPCH, maka kunci 256-bit harus berisi rantai berurutan karakter identik dengan angka dari 5 hingga 17. Artinya, sesuai dengan standar untuk GSPCH, sehingga memenuhi persyaratan kesamaan keacakan dengan keandalan 99,9%, GSPCH, dalam pengujian 2000 (mengeluarkan hasil dalam bentuk angka biner 256-bit) hanya akan memberikan hasil di mana panjang seri maksimum dari nilai yang sama: baik kurang dari 4, atau lebih dari 17.
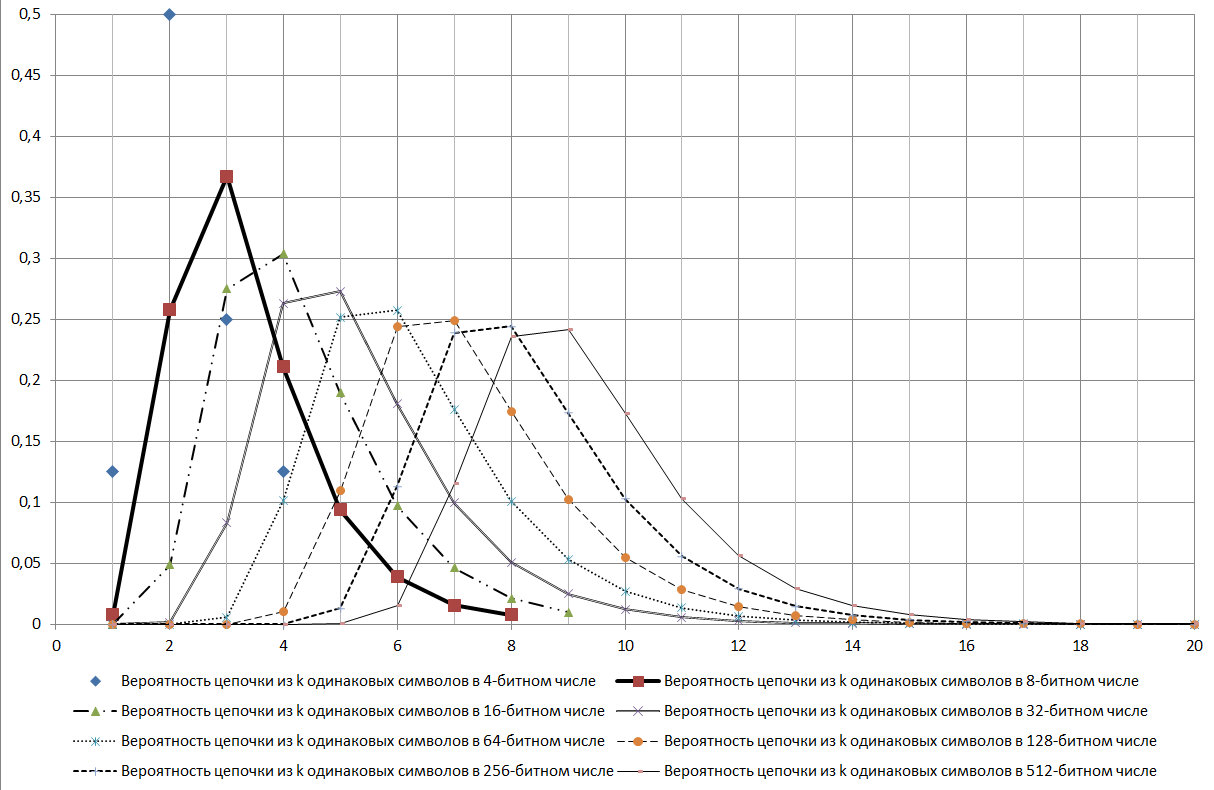
Fig. 17.
Seperti dapat dilihat dari diagram yang ditunjukkan pada Gambar 17, rantai log2N adalah mode untuk distribusi yang dipertimbangkan.
Selama penelitian, banyak tanda dari berbagai sifat dari urutan ini ditemukan. Inilah beberapa di antaranya:
- itu harus diuji dengan baik oleh kriteria chi-square;
- memberikan tanda-tanda adanya sifat fraktal;
- mungkin kriteria yang baik untuk mengidentifikasi berbagai proses acak.
Dan masih banyak lagi koneksi lainnya.
Memeriksa apakah urutan seperti itu juga ada pada
Ensiklopedia Sekuens
Integer On-Line (OEIS) (Ensiklopedia Online Urutan Integer) dalam nomor urut
A006980 , referensi dibuat untuk publikasi
JL Yucas, Menghitung set khusus kata-kata biner Lyndon, Ars Combin. , 31 (1991), hlm. 21-29 , di mana urutannya ditunjukkan pada halaman 28 (dalam tabel). Dalam publikasi, garis diberi nomor 1 lebih sedikit, tetapi nilainya sama. Secara umum, publikasi adalah tentang
kata-kata Lyndon , yaitu, sangat mungkin bahwa peneliti bahkan tidak curiga bahwa seri ini terkait dengan aspek ini.
Mari kita kembali ke teorema Erds-Renyi. Menurut hasil publikasi ini, dapat dikatakan bahwa dalam perumusan yang disajikan, teorema ini merujuk pada kasus umum, yang ditentukan oleh teorema Muavre-Laplace. Dan teorema yang ditunjukkan, dalam formulasi ini, tidak dapat menjadi kriteria yang jelas untuk keacakan seri. Tetapi fraktalitas, dan untuk kasus ini dinyatakan bahwa rantai dengan panjang yang ditunjukkan dapat dikombinasikan dengan rantai dengan panjang yang lebih panjang, tidak memungkinkan kita untuk menolak teorema ini dengan sangat jelas, karena ketidakakuratan dalam formulasi dimungkinkan. Contohnya adalah fakta bahwa jika untuk probabilitas 256-bit dari suatu bilangan di mana rantai maksimum 8 bit adalah 0,244235, maka, dalam hubungannya dengan urutan lain yang lebih panjang, probabilitas bahwa sejumlah 8 bit sudah ada dalam suatu bilangan sudah - 0,490234375. Sejauh ini, tidak ada peluang tegas untuk menolak teorema ini. Tetapi teorema ini sangat cocok di aspek lain, yang akan ditampilkan nanti.
Aplikasi praktis
Mari kita lihat contoh yang disajikan oleh pengguna VDG:
"... Cabang dendritik neuron dapat direpresentasikan sebagai urutan bit. Cabang, dan kemudian seluruh neuron, dipicu ketika rantai sinapsis diaktifkan di salah satu tempatnya. Neuron memiliki tugas untuk tidak menanggapi white noise, masing-masing, panjang minimum rantai, sejauh yang saya ingat dengan Numenty, adalah 14 sinapsis dalam neuron piramidal dengan 10 ribu sinapsisnya. Dan menurut rumus yang kita dapatkan: Log_ {2} 10000 = 13.287. Artinya, rantai yang panjangnya kurang dari 14 akan terjadi karena kebisingan alami, tetapi tidak akan mengaktifkan neuron. Benar-benar sempurna .
"Kami akan membuat grafik, tetapi dengan mempertimbangkan fakta bahwa Excel tidak mempertimbangkan nilai yang lebih besar dari 2 ^ 1024, kami akan membatasi diri pada jumlah sinapsis 1023 dan, dengan mempertimbangkan ini, kami akan menginterpolasi hasilnya dengan komentar, seperti yang ditunjukkan pada Gambar 18.

Fig. 18.
Ada jaringan saraf biologis yang dipicu ketika rantai m = log2N = 11 dikompilasi.Rantai ini adalah nilai modal, dan nilai ambang batas, probabilitas, dari beberapa jenis perubahan dalam situasi 0,78 tercapai. Dan probabilitas kesalahan adalah 1- 0,78 = 0,22. Misalkan rantai 9 sensor bekerja, di mana probabilitas menentukan acara adalah 0,37, masing-masing, probabilitas kesalahan adalah 1 - 0,37 = 0,63. Artinya, untuk mencapai penurunan dalam probabilitas kesalahan dari 0,63 menjadi 0,37, perlu bahwa 3,33 rantai dari 9 elemen bekerja. Perbedaan antara 11 dan 9 elemen adalah dari urutan ke-2, yaitu 2 ^ 2 = 4 kali, yang jika dibulatkan menjadi bilangan bulat, karena elemen tersebut memberikan nilai integer, maka 3,33 = 4. Kami melihat lebih jauh untuk mengurangi kesalahan saat memproses sinyal dari 8- elemen, kita sudah membutuhkan 11 rantai pemicu 8 elemen. Saya kira ini adalah mekanisme yang memungkinkan Anda menilai situasi dan membuat keputusan tentang mengubah perilaku objek biologis. Cukup masuk akal dan efisien, menurut saya. Dan dengan mempertimbangkan fakta bahwa kita tahu tentang alam yang menggunakan sumber daya semurah mungkin, hipotesis bahwa sistem biologis menggunakan mekanisme ini dibenarkan. Dan ketika kita melatih jaringan saraf, kita, pada kenyataannya, mengurangi kemungkinan kesalahan, karena untuk benar-benar menghilangkan kesalahan kita perlu menemukan hubungan analitis.
Kami beralih ke analisis data numerik. Dalam analisis data numerik, kami mencoba memilih ketergantungan analitis dalam bentuk y = f (xi). Dan pada tahap pertama kami menemukannya. Setelah menemukannya, seri yang ada dapat direpresentasikan sebagai biner, relatif terhadap persamaan regresi, di mana kami menetapkan 1 untuk nilai positif dan 0 untuk yang negatif, dan kemudian kami menganalisis serangkaian elemen identik. Kami menentukan yang terbesar, sepanjang rantai, distribusi rantai yang lebih pendek.
Selanjutnya, kita beralih ke teorema Erdos-Renyi, dari situ muncul bahwa ketika melakukan sejumlah besar tes dari nilai acak, rantai elemen identik harus dibentuk di semua register dari nomor yang dihasilkan, yaitu, m = log2N. Sekarang, ketika kita memeriksa data, kita tidak tahu apa sebenarnya volume seri itu. Tetapi jika Anda melihat ke belakang, maka rantai maksimum ini memberi kami alasan untuk menganggap bahwa R adalah parameter yang mencirikan bidang variabel acak, Gambar 19.
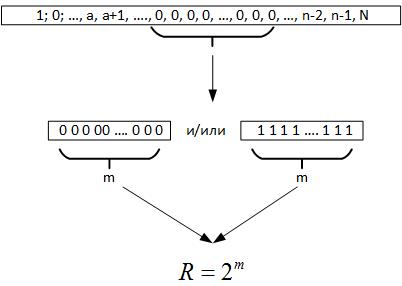
Fig. 19.
Artinya, membandingkan R dan N, kita dapat menarik beberapa kesimpulan:
- Jika R <N, maka proses acak diulang beberapa kali pada data historis.
- Jika R> N, maka proses acak memiliki dimensi lebih tinggi dari data yang tersedia, atau kami salah menentukan persamaan fungsi tujuan.
Kemudian untuk kasus pertama kami merancang jaringan saraf dengan sensor 2 ^ m, saya kira kita dapat menambahkan sepasang sensor untuk menangkap transisi, dan kami melatih jaringan ini pada data historis. Jika jaringan sebagai hasil pelatihan tidak dapat belajar dan akan menghasilkan hasil yang benar dengan probabilitas 50%, maka ini berarti bahwa fungsi tujuan yang ditemukan adalah optimal dan tidak mungkin untuk memperbaikinya. Jika jaringan dapat belajar, maka kami akan lebih meningkatkan ketergantungan analitis.
Jika dimensi seri lebih besar dari dimensi variabel acak, maka properti fraktalitas dari variabel acak dapat digunakan, karena setiap seri ukuran m berisi semua subruang dari dimensi yang lebih rendah. Saya kira dalam hal ini masuk akal untuk melatih jaringan saraf pada semua data kecuali rantai m.
Pendekatan lain untuk desain jaringan saraf mungkin periode perkiraan.
Sebagai kesimpulan, harus dikatakan bahwa, dalam perjalanan ke publikasi ini, banyak aspek ditemukan di mana besarnya dimensi variabel acak dan sifat-sifat yang ditemukan bersinggungan dengan tugas-tugas lain dalam analisis data. Tetapi untuk sekarang, ini semua dalam bentuk yang sangat mentah dan akan dibiarkan untuk publikasi di masa depan.
Bagian Sebelumnya:
Bagian 1 ,
Bagian 2