Posit-arithmetic: mengalahkan floating point di bidangnya sendiri. Bagian 2

Bagian 1

4. Perbandingan kuantitatif sistem numerik

4.1. Ketepatan desimal

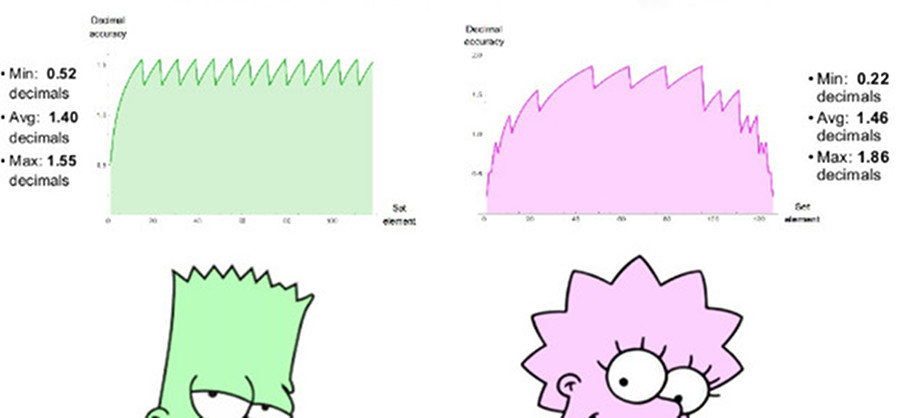
Akurasi adalah kebalikan dari kesalahan. Jika kita memiliki sepasang angka x dan y (bukan nol dan satu tanda), jarak di antara mereka dalam urutan besarnya adalah $$$\ mid log_ {10} (x / y) \ mid$ perintah desimal, ini adalah ukuran yang sama yang mendefinisikan rentang dinamis antara bilangan positif terkecil dan terbesar yang dapat diwakili x dan y. Distribusi ideal angka sepuluh antara 1 dan 10 dalam sistem bilangan real bukan distribusi angka yang merata dari 1 hingga 10, tetapi eksponensial: $$$1, 10 ^ {1/10}, 10 ^ {2/10}, ..., 10 ^ {9/10}, 10$ . Ini adalah skala desibel yang digunakan oleh insinyur untuk waktu yang lama untuk mengekspresikan hubungan, misalnya, 10 desibel adalah rasio sepuluh kali lipat. 30db berarti koefisien $$$10 ^ 3 = 1000$ . Rasio 1db adalah faktor sekitar 1,26, jika Anda tahu nilainya dengan akurasi 1db, Anda memiliki akurasi 1 tempat desimal. Jika Anda tahu nilai dengan akurasi 0,1 db, ini berarti 2 tanda akurasi, dll. Rumus presisi desimal adalah $$$log_ {10} (1 / \ mid log_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ , di mana x dan y adalah nilai valid yang dihitung dengan menggunakan sistem pembulatan, seperti yang digunakan dalam format float dan posit, atau batas atas dan bawah jika sistem yang ketat menggunakan interval digunakan, atau nilai yang valid.

4.2. Mendefinisikan float dan menempatkan set perbandingan

Kita dapat membuat model skala angka float dan posit masing-masing sepanjang 8 bit. Keuntungan dari pendekatan ini adalah bahwa 256 nilai cukup kecil sehingga kami dapat mengujinya sepenuhnya dan membandingkan semuanya $$$256 ^ 2$ kemunculan dalam tabel untuk operasi penambahan, pengurangan, perkalian, dan pembagian. Bilangan real dengan akurasi 1/4 memiliki satu bit tanda, empat bit eksponen dan tiga bit bagian fraksional, dan mematuhi semua aturan IEEE 754. Angka positif terkecil (didenormalkan) adalah 1/1024, positif terbesar adalah 240, rentang dinamis asimetris dan sama 5,1 perintah desimal.kombinasi 14 bit mewakili NaN.

Penggunaan 8-bit yang sebanding menggunakan es = 1, memiliki rentang angka positif dari 1/4096 hingga 4096, rentang dinamis simetris 7,2 pesanan desimal. Tidak ada nilai NaN. Kita dapat memplot grafik presisi desimal angka positif di kedua set, seperti yang ditunjukkan pada gambar. 7. Perhatikan bahwa nilai-nilai yang diwakili oleh angka posit memiliki dua orde desimal besarnya rentang dinamis yang lebih besar daripada angka float, dan akurasinya sama atau lebih besar untuk semua nilai kecuali yang angka floatnya dekat dengan overflow atau anti-overflow. Indentasi grafik untuk kedua sistem adalah perkiraan logaritmik dari fungsi linear piecewise. Dalam angka float, akurasi berkurang hanya di sebelah kiri, di area dekat dengan anti-kepribadian, di sebelah kanan, fungsi terputus, karena kemudian muncul nilai-nilai NaN. Angka-angka posit memiliki fungsi presisi penurunan yang lebih simetris di sekitar tepi.


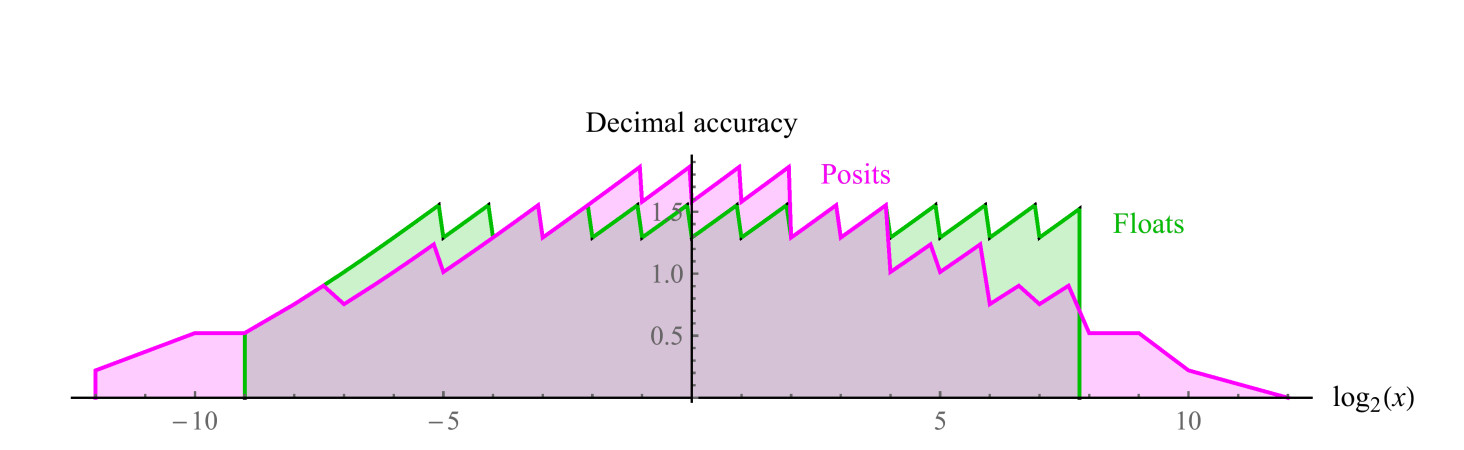
Fig. 7. Perbandingan presisi desimal angka float dan posit

4.3. Membandingkan operasi argumen tunggal

4.3.1. Nilai terbalik

Untuk setiap input x nilai yang mungkin dari fungsi 1 / x, hasilnya dapat persis sesuai dengan nilai lain dalam set yang diberikan, atau dapat dibulatkan, dalam hal ini kita dapat mengukur kesalahan desimal menggunakan rumus dari bagian 4.1, untuk angka float, hasilnya dapat menyebabkan melimpah atau NaN. Lihat gbr. 8.



Fig. 8. Perbandingan kuantitatif angka float dan posit ketika menghitung nilai terbalik

Kurva pada grafik kanan menunjukkan besarnya kesalahan dalam menghitung nilai terbalik, sedangkan angka float dapat menghasilkan NaN. Angka posisi lebih unggul daripada mengambang dalam banyak kasus, dan keunggulan ini dipertahankan sepanjang rentang. Menghitung kebalikan dari angka float yang didenormalisasi mengarah ke overflow, yang mengarah ke nilai kesalahan tak terbatas, dan, tentu saja, argumen NaN memberikan kebalikan dari NaN. Nomor posit ditutup relatif terhadap perhitungan nilai terbalik.

4.3.2. Akar kuadrat

Fungsi akar kuadrat tidak mengarah pada overflow atau anti-overflow. Untuk argumen negatif, dan untuk NaN, hasilnya adalah NaN. Ingatlah bahwa kita memiliki "model skala" angka float dan posit, kelebihan posit meningkat dengan meningkatnya akurasi data. Untuk float dan posit 64-bit, kesalahan posit akan menjadi sekitar 1/30 dari kesalahan float, bukannya 1/2.

4.3.3. Kotak

Operasi unary umum lainnya adalah $$$x ^ 2$ . Overflow dan anti-overflow sering terjadi ketika mengkuadratkan float. Untuk hampir setengah pelampung, mengkuadratkan tidak menghasilkan hasil yang bermakna, sementara mengkuadratkan angka posit ke dalam kuadrat selalu menghasilkan angka posit (kuadrat tanpa tanda tak terhingga adalah tak terhingga tanpa tanda pengenal).


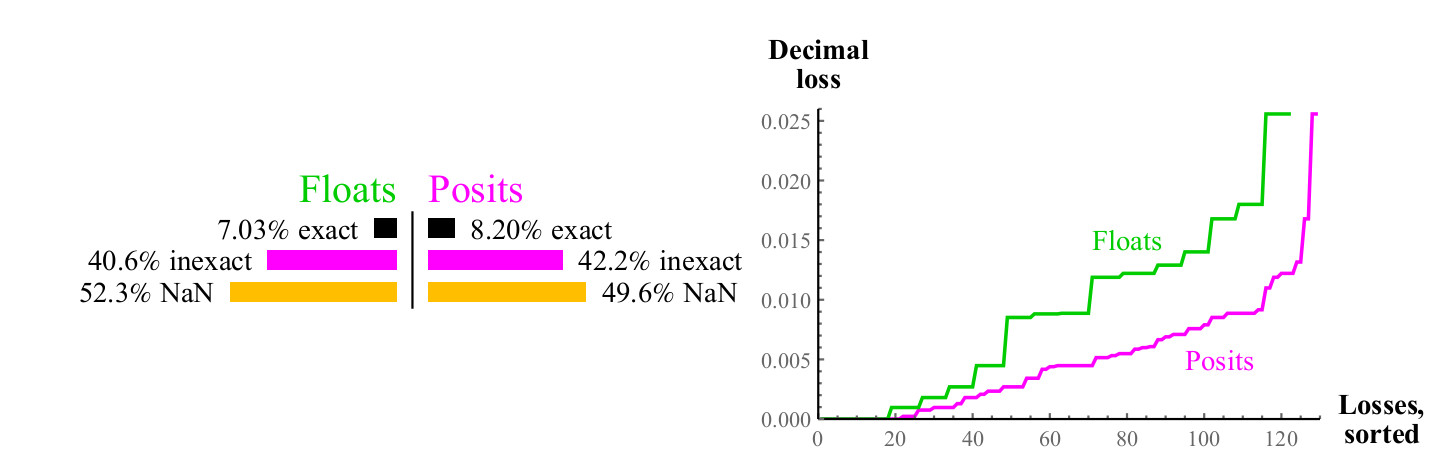
Fig. 9. Perbandingan kuantitatif angka float dan posit ketika menghitung $$$\ sqrt x$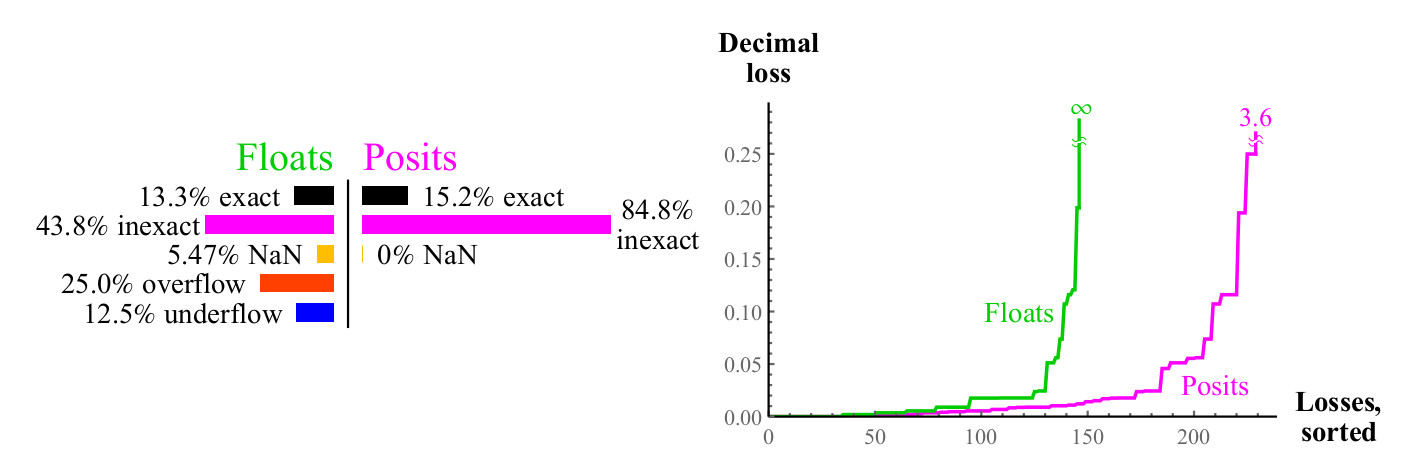


Fig. 10. Perbandingan kuantitatif angka float dan posit ketika menghitung $$$x ^ 2$

4.3.4. Logaritma Basis 2

Kami juga membuat perbandingan untuk mencakup fungsi logaritma basis 2, yaitu persentase kasus di mana $$$log_2 (x)$ dapat direpresentasikan secara akurat, dan jika tidak dapat direpresentasikan secara akurat, berapa banyak tempat desimal yang hilang. Angka float memiliki satu-satunya keunggulan dalam hal ini: angka float dapat digunakan untuk mewakili $$$log_2 (0)$ bagaimana $$$- \ infty$ dan $$$log_2 (\ infty)$ bagaimana $$$\ infty$ , tapi ini lebih dari diimbangi oleh kamus besar kekuatan integer dua untuk nomor posit.


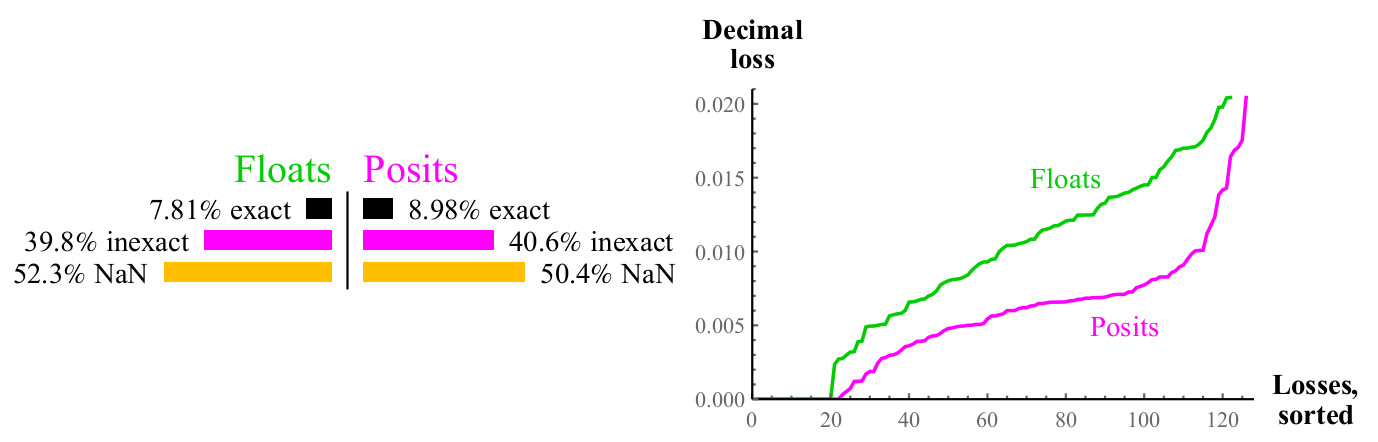
Fig. 11. Perbandingan kuantitatif angka float dan posit ketika menghitung $$$log_2 (x)$

Grafik ini mirip dengan yang untuk akar kuadrat, sekitar setengah dari kasus memberikan NaN dalam kedua kasus, tetapi angka-angka menempatkan memiliki setengah kehilangan presisi desimal. Jika Anda bisa menghitung $$$log_2 (x)$ , Anda hanya perlu mengalikan hasilnya dengan faktor penskalaan untuk mendapatkan $$$ln (x)$ atau $$$log_ {10} (x)$ atau logaritma dengan alasan lain.

4.3.5. Peserta pameran $$$2 ^ x$

Begitu pula jika Anda bisa menghitung $$$2 ^ x$ , Anda dapat dengan mudah menggunakan faktor penskalaan untuk mendapatkan $$$e ^ x$ atau $$$10 ^ x$ dll. Nomor posit memiliki satu pengecualian, $$$2 ^ x$ sama dengan NaN ketika argumennya adalah $$$\ pm \ infty$ .


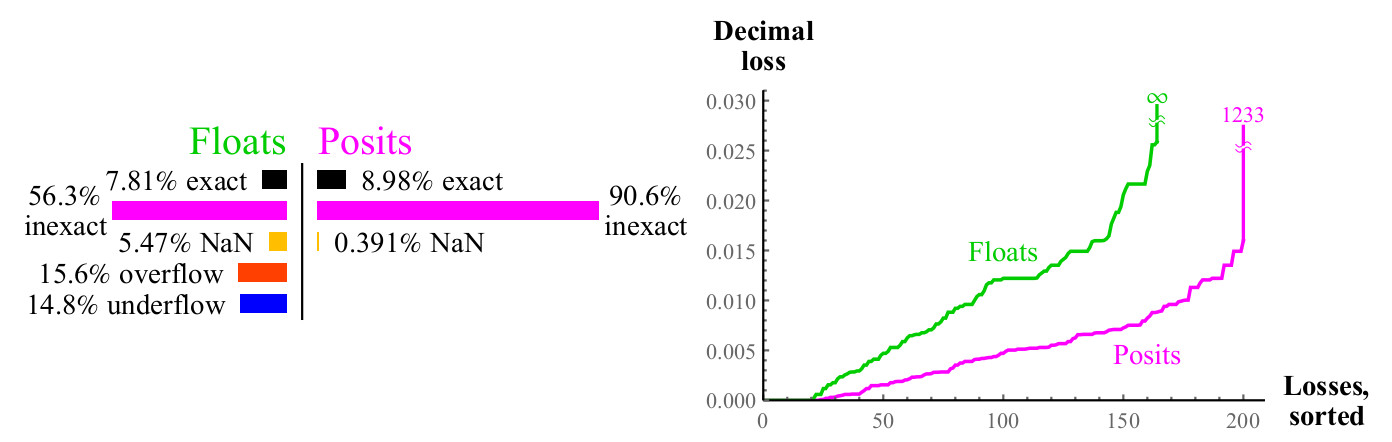
Fig. 12. Perbandingan kuantitatif angka float dan posit ketika menghitung $$$2 ^ x$

Kehilangan desimal maksimum untuk nomor positip mungkin tampak besar sejak itu $$$2 ^ {maxpos}$ akan dibulatkan kembali ke maxpos. Dalam contoh ini, hanya sejumlah kecil kesalahan yang sebesar $$$log_ {10} (24096) \ approx1233$ pesanan desimal. Putuskan mana yang lebih baik: kehilangan lebih dari seribu pesanan desimal, atau kehilangan pesanan desimal dalam jumlah tak terbatas ? Jika Anda tidak dapat menggunakan angka begitu besar, posit angka masih menang, karena kesalahan dengan nilai kecil jauh lebih baik. Dalam semua kasus ketika Anda kehilangan sejumlah besar perintah desimal saat menggunakan angka posit, argumen input jauh melampaui apa yang bahkan dapat diungkapkan oleh angka float. Grafik menunjukkan bagaimana angka-angka posit lebih stabil dalam hal rentang dinamis di mana hasilnya masuk akal, dan lebih unggul dalam akurasi dalam kisaran ini.

Untuk operasi unary biasa $$$1 / x, \ sqrt x, x ^ 2, log_2 (x)$ dan $$$2 ^ x$ , nomor posit sepenuhnya dan selalu lebih akurat daripada angka float dengan jumlah bit yang sama, dan menghasilkan hasil yang bermakna dalam rentang dinamis yang luas. Kami sekarang mengalihkan perhatian kami ke empat operasi aritmatika dasar yang memiliki dua argumen: penjumlahan, pengurangan, perkalian, dan pembagian.

4.4. Membandingkan operasi dua argumen

Kita dapat menggunakan model skala sistem bilangan untuk mempelajari operasi aritmatika dari dua argumen, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Untuk memvisualisasikan 65536 hasil, kami membuat "grafik cakupan" 256 * 256, yang dengan jelas menunjukkan berapa proporsi hasil yang akurat, tidak akurat, menyebabkan overflow, anti-overflow atau NaN.

4.4.1. Penambahan dan Pengurangan

Sejak $$$x - y = x + (- y)$ berfungsi baik untuk float dan posit, tidak perlu mempelajari pengurangan secara terpisah. Untuk operasi penambahan, kami menghitung nilai yang tepat $$$z = x + y$ , dan bandingkan dengan jumlah yang dikembalikan di masing-masing sistem angka. Mungkin terjadi bahwa hasilnya tidak akurat, maka harus dibulatkan ke angka bukan nol hingga terdekat, overflow atau anti-overflow, atau ketidakpastian bentuk dapat terjadi $$$\ infty- \ infty$ yang menghasilkan NaN. Masing-masing kasing ini ditandai dengan warna, dan sekilas kita dapat membahas seluruh tabel tambahan. Dalam kasus pembulatan hasil, warna berubah dari hitam (nilai tepat) menjadi ungu (nilai tepat untuk posit dan float). Fig. 13 menunjukkan seperti apa grafik cakupan untuk angka float dan unum. Seperti halnya operasi unary, tetapi memiliki lebih banyak poin, kita dapat menarik kesimpulan tentang kemampuan setiap sistem angka untuk memberikan jawaban yang bermakna dan akurat:


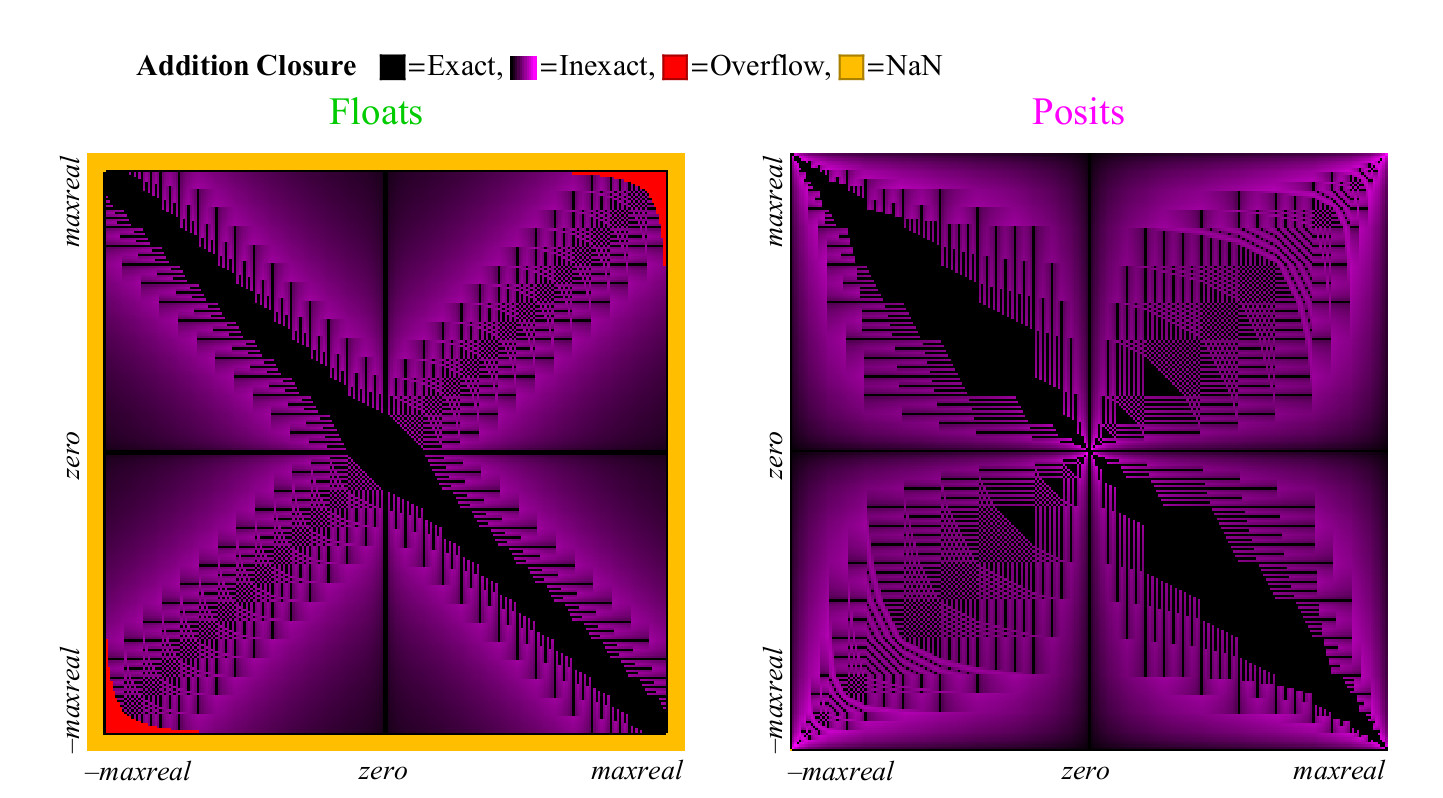
Fig. 13. Grafik cakupan penuh untuk menambahkan angka float dan posit


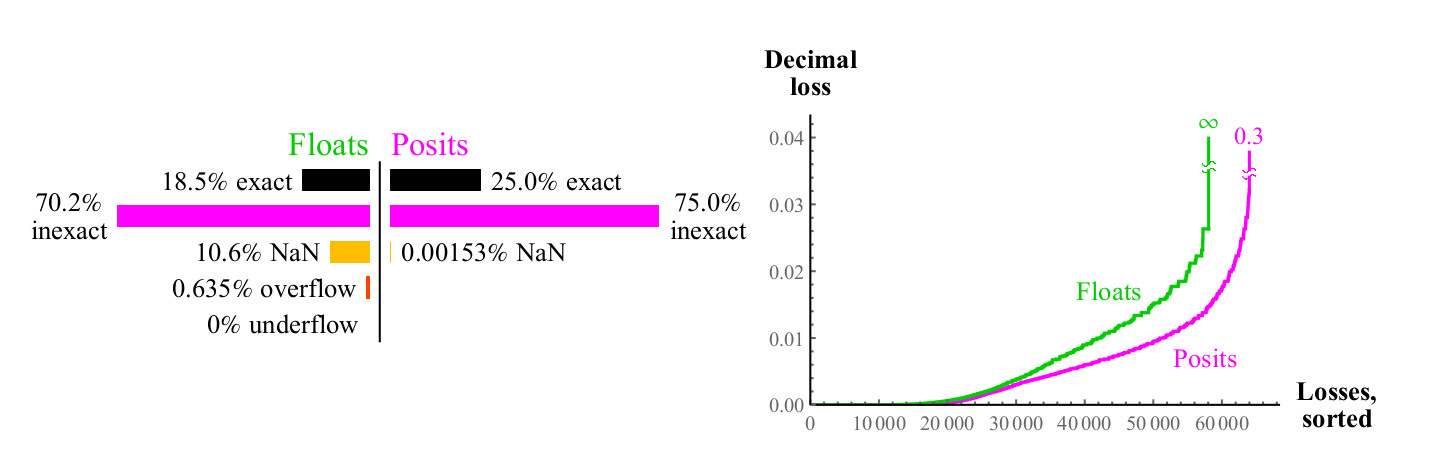
Fig. 14. Perbandingan kuantitatif angka float dan posit untuk penambahan

Pada pandangan pertama, menjadi jelas bahwa posit memiliki lebih banyak poin pada grafik tambahan di mana hasilnya akurat. Strip diagonal hitam lebar pada grafik cakupan untuk float jauh lebih luas daripada yang akan terjadi untuk akurasi yang lebih besar, karena itu mewakili zona bilangan denormalized di mana bilangan float ditempatkan pada interval yang sama, seperti angka titik tetap, angka tersebut membentuk proporsi besar dari jumlah total hanya dalam hal angka 8-bit.

4.4.2. Perkalian

Kami menggunakan pendekatan yang sama untuk membandingkan seberapa baik angka float dan posit bertambah banyak. Tidak seperti penambahan, perkalian dapat menyebabkan anti-overflow dari angka float. "Anti-overflow bertahap", zona yang dapat Anda lihat di tengah pada Gambar. 15. ke kiri. ( artinya angka yang dinormalisasi. kira-kira diterjemahkan. ) Tanpa zona ini, zona anti-meluap biru akan memiliki bentuk berlian. Grafik perkalian untuk nomor posit kurang berwarna, yang lebih baik. Hanya dua piksel yang disorot sebagai NaN, dekat dengan tempat di mana tanda nol sumbu berada ( piksel berada paling kiri di tengah secara vertikal dan bagian bawah di tengah secara horizontal. Approx. Transl. ) Ada hasil penggandaan $$$\ pm \ infty \ cdot 0 = NaN$ . Angka float memiliki lebih banyak kasus di mana produk tersebut akurat tetapi dengan harga yang mengerikan. Seperti yang ditunjukkan pada Gambar. 15, hampir 1/4 dari semua produk float mengarah ke overflow atau anti-overflow, dan fraksi ini tidak berkurang dengan meningkatnya akurasi float.


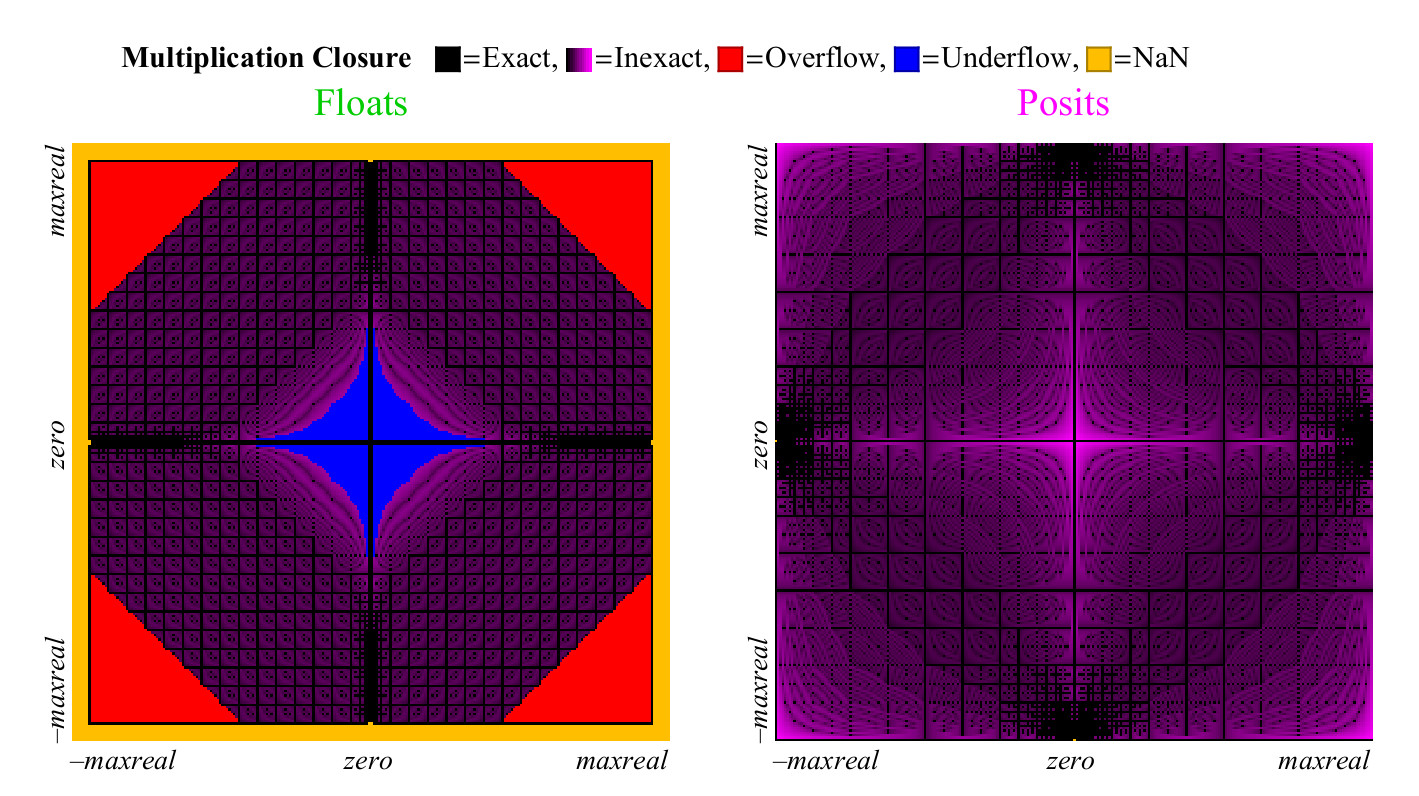
Gambar 15. Grafik cakupan penuh untuk mengalikan angka float dan posit

Kasus pembulatan terburuk untuk nomor posit terjadi ketika $$$maxpos \ times maxpos$ yang dibulatkan lagi ke maxpos. Untuk kasus seperti itu (sangat jarang), kesalahannya adalah 3,6 desimal pesanan. Seperti grafik dalam gambar. 16, nomor posit secara signifikan lebih baik daripada float, meminimalkan kesalahan multiplikasi.


Fig. 16. Perbandingan kuantitatif angka float dan posit untuk perkalian

Grafik cakupan untuk operasi divisi mirip dengan grafik untuk perkalian, tetapi zona ditukar, untuk menghemat ruang, tidak ditampilkan di sini. Indikator kuantitatif untuk pembagian hampir sama dengan untuk perkalian.

4.5. Perbandingan angka float dan posit untuk mengevaluasi ekspresi

4.5.1. Uji “anggaran presisi 32-bit”

Tes biasanya dilakukan berdasarkan runtime minimum, dan seringkali tidak memberikan gambaran lengkap tentang seberapa akurat hasilnya. Jenis lain dari tes adalah satu di mana kami memperbaiki anggaran kesalahan, yaitu, jumlah bit per variabel, dan mencoba untuk mendapatkan akurasi desimal maksimum sebagai hasilnya. Ini adalah contoh ekspresi yang bisa kita gunakan untuk membandingkan sistem numerik dengan anggaran 32 bit per angka:

$$

$$X = \ kiri (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ kanan) ^ {67/16} = 302.8827196 \ dotsb$$

Aturannya adalah kita mulai dengan representasi angka terbaik $$$\ pi$ dan $$$e$ , mungkin di masing-masing sistem numerik, dan representasi dari semua bilangan bulat yang ditunjukkan, dan kami melihat berapa banyak angka desimal yang cocok dengan nilai X yang sebenarnya setelah melakukan sembilan operasi dalam ekspresi. Kami akan menyoroti angka yang salah dengan warna oranye .

Terlepas dari kenyataan bahwa angka float IEEE 32-bit memiliki presisi desimal, yang berkisar antara 7,3 hingga 7,6 pesanan desimal, akumulasi kesalahan pembulatan dalam perhitungan X memberikan jawaban 302. 912 , yang hanya memiliki tiga digit yang valid. Ini adalah salah satu alasan mengapa pengguna merasa perlu menggunakan float 64-bit di mana-mana, karena bahkan ekspresi sederhana pun berisiko kehilangan akurasi sehingga hasilnya mungkin tidak berguna.

Angka posisi 32-bit memiliki presisi desimal variabel, yang berkisar antara 8,2 dan 8,5 pesanan desimal untuk angka-angka dengan nilai absolut sekitar 1. Ketika menghitung X, angka itu memberi kita jawaban 302,882 31 , yang memiliki dua kali lebih banyak digit signifikan. Juga jangan lupa bahwa angka posisi 32-bit memiliki rentang dinamis lebih dari 144 tempat desimal, dan float 32-bit memiliki rentang dinamis yang jauh lebih kecil yaitu 83 bit. Oleh karena itu, akurasi tambahan hasil tidak tercapai dengan mempersempit rentang dinamis.

4.5.2. Tes Empat Kali Lipat: Masalah Triangle Tipis Goldberg

Ada masalah klasik "segitiga tipis" [1]: temukan luas segitiga dengan sisi a , b , c ketika dua sisi b dan c hanya 3 unit dari angka paling tidak signifikan (Unit di Tempat Terakhir, ULP) lebih panjang dari setengah panjangnya. sisi (Gbr. 17).


Fig. 17. Masalah Segitiga Tipis Goldberg

Rumus klasik untuk area A menggunakan variabel antara s:

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s (s-a) (s-b) (s-c)}$$

Bahaya dalam rumus ini adalah bahwa s sangat dekat dengan nilai a , dan perhitungannya $$$(s-a)$ meningkatkan kesalahan pembulatan sangat banyak. Mari kita coba angka float IEEE 128-bit (dengan akurasi empat kali lipat) $$$a = 7, b = c = 7/2 + 3 \ kali 2 ^ {- 111}$ . (Jika Anda mengambil tahun cahaya sebagai unit pengukuran, sisi pendek akan lebih panjang dari setengah sisi panjang dengan hanya 1/200 dari diameter proton. Tapi ini membuat segitiga tinggi pintu di atas.) Kami juga menghitung nilai A menggunakan nomor pos 128-bit ( es = 7). Berikut ini adalah hasilnya:

$$$$ menampilkan $$ \ begin {matrix} \ textrm {Nilai sebenarnya:} & 3.14784204874900425235885265494550774498 \ titik \ kali 10 ^ {- 16} \\ \ textrm {float IEEE 128-bit:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ titik \ kali 10 ^ {- 16} \\ \ textrm {128-bit posit:} & 3.147842048749004252358852654945507777 \ warna {orange} {39} \ dots \ kali 10 ^ {- 16} end {matrix} tampilkan $$

Jumlah angka memiliki hingga 1,8 digit desimal presisi yang lebih besar dari float presisi empat kali lipat dalam rentang dinamis luas: dari $$$2 \ kali 10 ^ {- 270}$ sebelumnya $$$5 \ kali 10 ^ {- 269}$ . Ini cukup untuk mencegah konsekuensi bencana dari peningkatan kesalahan dalam kasus khusus ini. Menarik juga untuk dicatat bahwa jawaban dalam format posit akan lebih akurat daripada dalam format float, bahkan jika pada akhirnya kami mengubahnya menjadi posit 16-bit.

4.5.3. Solusi dari persamaan kuadratik

Ada trik klasik yang dirancang untuk menghindari kesalahan pembulatan saat menghitung root $$$r_1$ , $$$r_2$ persamaan $$$ax ^ 2 + bx + c = 0$ menggunakan rumus biasa $$$r_1, r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ ketika b jauh lebih besar dari a dan c , yang mengarah pada hilangnya digit di sebelah kiri $$$\ sqrt {b ^ 2-4ac}$ sangat dekat dengan b . Tetapi alih-alih memaksa pemrogram untuk menghafal trik mistis, mungkin lebih baik untuk membuat perhitungan aman dengan menggunakan rumus sederhana dari tutorial. Taruh $$$a = 3, b = 100, c = 2$ dan bandingkan hasilnya dalam format float dan posit 32-bit.

Tabel 5. Solusi persamaan kuadratik


Root tidak stabil secara numerik - $$$r_1$ , tetapi perhatikan bahwa posit 32-bit memberikan 6 digit yang benar, bukan 4 untuk float.

4.6. Perbandingan sistem float dan Posit untuk tes LINPACK klasik

Untuk waktu yang lama, metode utama untuk mengevaluasi superkomputer adalah pemecahan $$$n \ kali n$ sistem persamaan linear $$$\ mathbf Ax = b$ . Yaitu, tes mengisi matriks A dengan angka pseudo-acak dari 0 hingga 1, dan vektor b dengan jumlah baris A. Ini berarti bahwa solusi x adalah vektor yang terdiri dari unit. Tes menghitung tingkat deduksi $$$\ | \ mathbf Ax-b \ |$ untuk memverifikasi kebenaran, meskipun tidak ada angka yang sulit yang harus benar dalam jawabannya. Hilangnya beberapa digit akurasi khas untuk pengujian, dan float 64-bit biasanya digunakan (belum tentu IEEE). Awalnya, tes disediakan untuk n = 100, tetapi ukuran ini terlalu kecil untuk superkomputer tercepat, jadi n ditingkatkan menjadi 300, lalu menjadi 1000, dan akhirnya (dari penulis pertama), tes menjadi scalable dan memberikan jumlah operasi per detik, berdasarkan pada kenyataan bahwa tes melakukan $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ operasi multiplikasi dan penambahan.

Membandingkan posit dan float, kami mencatat sedikit kelemahan dari tes: jawaban dalam kasus umum bukanlah urutan unit, karena kesalahan pembulatan dalam jumlah dalam garis. Kesalahan seperti itu dapat dihilangkan jika kita menemukan bagaimana kemunculan dalam A berkontribusi 1 bit, yang berada di luar kisaran akurasi yang mungkin, dan mengatur bit ini ke 0. Ini akan memberi kita keyakinan bahwa jumlah baris A dapat diwakili tanpa pembulatan, dan bahwa jawabannya adalah x sebenarnya adalah vektor yang terdiri dari unit. Untuk versi asli tugas, dengan ukuran 100x100, float IEEE 64-bit memberikan jawaban seperti ini:

0.9999999999999 633626401873698341660201549530029296875
1,00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1,0000000000000 22648549702353193424642086029052734375

Tidak satu pun dari 100 angka yang benar; mereka mendekati 1 tetapi tidak pernah sama dengan 1. Dengan angka posit, kita dapat melakukan hal yang luar biasa. Menggunakan angka posit 32-bit dan algoritma yang sama, kami menghitung residu$$$r = \mathbf Ax − b$menggunakan operasi gabungan adalah produk skalar. Kemudian putuskan$$$\mathbf Ax'=r$ (menggunakan sudah diproses $$$\mathbf A$ ) dan gunakan $$$x'$ untuk koreksi: $$$x \leftarrow x-x'$ . Hasilnya adalah jawaban akurat yang belum pernah terjadi sebelumnya untuk tes LINPACK: $$$\{1, 1,...,1\}$ .Dapatkah aturan LINPACK melarang penggunaan tipe angka 32-bit baru, yang penggunaannya memungkinkan untuk mencapai hasil sempurna dengan kesalahan nol, atau terus bersikeras pada penggunaan float 64-bit, yang tidak mengizinkan ini? Keputusan ini akan dibuat oleh mereka yang bertanggung jawab atas tes ini. Bagi mereka yang perlu memecahkan sistem persamaan linear untuk menyelesaikan masalah nyata, daripada membandingkan kecepatan superkomputer, posit menawarkan keunggulan yang menakjubkan.

5. Kesimpulan

Mengalahkan float di gimnya sendiri: dengan itu, Anda dapat melakukan perhitungan dan mengurangi kesalahan pembulatan. Jumlah positimasi lebih besar, rentang dinamis lebih besar, dan rentang lebih luas. Dapat digunakan untuk mendapatkan hasil yang lebih baik dari pelampung dengan kedalaman bit yang sama, atau (yang bisa menjadi keunggulan kompetitif yang lebih besar), hasil yang sama dengan kedalaman bit yang lebih reng Karena bandwidth sistem terbatas, gunakan operan yang lebih kecil berarti kecepatan lebih cepat dan konsumsi daya yang lebih rendah.
Karena mereka bekerja sebagai pelampung, dan bukan sebagai sistem interval, mereka dapat dianggap sebagai pengganti langsung pelampung, seperti yang ditunjukkan di sini. Jika algoritma menggunakan float lulus tes, dan waktu dan stabilitas "cukup baik", maka itu akan bekerja lebih baik lagi dengan posit. Operasi menyatu yang tersedia di posit menyediakan alat yang ampuh untuk mencegah akumulasi kesalahan pembulatan, dan dalam beberapa kasus memungkinkan Anda untuk menggunakan nomor posit 32-bit dengan aman alih-alih mengapung 64-bit dalam aplikasi yang membutuhkan kinerja tinggi. Secara umum, ini akan meningkatkan kinerja aplikasi sebanyak 2-4 kali, dan mengurangi konsumsi daya, menghemat energi dan mengurangi biaya penyimpanan data. Posisi dukungan perangkat keras akan memberi kita setara dengan satu atau dua langkah Hukum Moore,tanpa perlu mengurangi ukuran transistor atau menambah biaya. Tidak seperti float, sistem posisi memberikan sedikit demi sedikit reproduksi hasil pada sistem yang berbeda, menghilangkan kelemahan utama dari standar IEEE 754. Angka-angka posisi lebih sederhana dan lebih elegan daripada float, dan mengurangi jumlah peralatan untuk mendukungnya. Meskipun angka float ada di mana-mana sekarang, nomor posit mungkin segera membuatnya usang.

Referensi:

1. David Goldberg. Apa yang harus diketahui oleh setiap ilmuwan komputer tentang aritmatika titik-mengambang.
ACM Computing Survey (CSUR), 23 (1): 5-48, 1991. DOI: doi: 10.1145 / 103162.103163.
2. John L Gustafson. The End of Error: Unum Computing, volume 24. CRC Press, 2015.
3. John L Gustafson. Melampaui Titik Mengambang: Aritmatika Komputer Generasi Selanjutnya. Seminar Stanford: https://www.youtube.com/watch?v=aP0Y1uAA-2Y , 2016. transkripsi lengkap
tersedia di http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. John L Gustafson. Pendekatan radikal untuk perhitungan dengan bilangan real. Superercomputing
Frontiers and Innovations, 3 (2): 38–53, 2016. doi: http://dx.doi.org/10.14529/jsfi160203.
5. John L Gustafson. Debat Hebat @ ARITH23. https://www.youtube.com/watch?v=
KEAKYDyUua4 , 2016. transkripsi lengkap tersedia di http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. Ulrich W Kulisch dan Willard L Miranker. Pendekatan baru untuk perhitungan ilmiah, volume 7. Elsevier, 2014.
7. Situs Lainnya. Standar IEEE untuk aritmatika floating-point. IEEE Computer Society, 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. Isaac Yonemoto. https://github.com/interplanetary-robot/SigmoidNumbers