Kebetulan sains berkembang tidak merata, dan karena itu dalam kehidupan kita hari ini, bisa dikatakan, ada tempat untuk berprestasi. Suatu prestasi, tentu saja, ilmiah, tetapi dari ini tidak kalah pentingnya. Dan sekarang, para pembaca, Anda diberi kesempatan untuk melihat tempat feat, harga resmi untuk pembayarannya (seperti kebiasaan di negara-negara yang menyebut diri mereka beradab), dan bahkan mencoba keberuntungan Anda sendiri. Nah, pada saat yang sama, setidaknya beberapa dari Anda akan merasakan pesona menemukan mutiara dalam hal yang sangat biasa.
Selanjutnya, dalam beberapa seri, sebuah cerita akan diikuti tentang hal-hal yang dapat diakses oleh lulusan sekolah menengah mana pun (dan bahkan banyak anak sekolah). Tidak akan ada bukti, karena mereka sering jelas, dan jika disajikan di sini mereka tidak hanya akan memperluas volume, tetapi juga akan menakuti banyak pembaca.
Seri pertama
Pertama ada bintang. Ada proses bermain dengan mereka, melihat dan merasakan, melemparkan dan mengamati jalan jatuh yang bersinar. Bintang-bintang adalah pola. Dan jumlahnya adalah kotak pasir. Angka-angka berubah di sisi baru, dan bintang lain muncul di celah di antara mereka. Kilauannya memberi isyarat dan, yang paling penting, tidak terbakar, tetapi membiarkan dirinya disentuh, diangkat, dan kemudian melambai kepada mereka untuk meninggalkan jejak debu bintang yang berkilau. Tapi kemudian bintang-bintang menjadi akrab dan ada satu pekerjaan yang tersisa untuk memilah mereka. Dan kemudian sebuah ide muncul.
Idenya sederhana - Anda dapat menghasilkan uang darinya. Dan ya, itu benar-benar termotivasi. Tapi itu tidak tumbuh bersama. Itu menghibur, ada bintang biasa yang bersinar dengan cara baru, ada kesenangan dan ada kemajuan. Hanya pada akhirnya muncul sebuah hutan, hutan berkelanjutan dari pohon-pohon yang bersinar. Dan saya lemah, saya tidak bisa mengurutkan taiga ini untuk mencari cahaya sejati, karena ada jutaan pohon, dan saya sendirian. Oleh karena itu, saya sarankan Anda melihat bintang-bintang, dan jika mereka menarik, maka Anda bisa mendapatkan $ 400K, tetapi kenyataannya ada satu "tetapi" - di hutan Anda harus dapat memilih jalan yang benar.
Tentang pendekatan terhadap bintang-bintang
Apa itu angka? Di satu sisi, itu adalah produk dari pikiran suram kita, tidak ditemukan di alam. Tetapi di sisi lain, abstraksi semacam itu memungkinkan kita untuk memodelkan banyak proses yang kita amati semua dalam sifat yang sama. Hanya modelnya yang tidak sama dengan fenomena yang diamati. Jadi sekali lagi kita berhadapan dengan adaptasi terhadap kemampuan sederhana kita dalam menggambarkan alam. Apakah ini bagus? Dalam hal akurasi, uraiannya tidak terlalu bagus. Bukan karena seseorang mungkin tidak memiliki cukup banyak tempat desimal, tetapi karena fenomena model yang tidak akurat dapat sangat mengejutkan kita ketika ternyata model tersebut tidak memiliki satu atau fitur spesifik lain yang hadir dalam kenyataan dan bahkan kadang-kadang terdengar sedikit mengganggu. naturalis lalai di kepala.
Sehubungan dengan hal tersebut di atas, mari kita coba untuk menanyakan tentang kelengkapan dasar dari setiap pemodelan - kelengkapan memahami konsep angka. Hanya sejumlah, hanya pengetahuan tentang hal itu, diletakkan sejak masa kanak-kanak, tampaknya - yah, apa lagi itu? Tapi di sana kita bisa menemukan jurang. Ya, yang tanpa dasar, dan yang penuh bintang.
Tidak ada angka di alam. Namun secara alami Anda bisa melihat hubungannya. Awan lebih besar (lebih lama / lebih luas / lebih tebal / seperti_Anda lain_akan_baik) awan lain, yang berarti ada tempat untuk korelasi. Tetapi rasionya juga tidak memiliki angka. Hanya ada dua awan, satu lagi, yang lain lebih sedikit, dan ada perbandingannya. Meskipun ya, rasionya juga ditemukan oleh manusia. Karena itu, orang mungkin bertanya - apa gunanya? Manfaatnya adalah ini - konsep korelasi selangkah lebih maju dari konsep angka. Pada awalnya ada rasio, dan baru kemudian angka muncul. Lebih tepatnya - angka pecahan. Karena itu, memahami hubungan, kita akan mengerti angka-angka.
Bagaimana bilangan pecahan diperoleh? Sangat sederhana - dari kebutuhan untuk memodelkan korelasi. Pada awalnya ada rasio langkah dan sisi tanah, domba dari satu pemilik ke domba dari yang lain, berat satu semangka ke berat yang lain. Dalam semua kasus ini, ada kebutuhan untuk mengekspresikan perbedaan. Tetapi perbedaannya tidak dibagi secara ketat dengan jumlah anak tangga atau ukuran semangka tetangga. Pada awalnya mereka belajar mengekspresikan perbedaan dengan membaginya menjadi satuan ukuran yang lebih kecil (siku ditambahkan ke langkah-langkah, dan jari ditambahkan ke siku). Tetapi sains tidak tinggal diam dan menuntut keakuratan yang semakin besar. Akibatnya, semua orang sepakat pada keseragaman, lupa tentang jari, siku, langkah dan pound lainnya dengan sterling. Keseragaman dinyatakan dalam jumlah.
Bagaimana cara mengkorelasikan dua segmen jika salah satu dari mereka tidak cocok dengan yang lainnya bilangan bulat beberapa kali? Anda dapat mengukur dengan jari-jari Anda, tetapi akan lebih akurat untuk mengambil segmen yang lebih kecil sebagai unit pengukuran dan membaginya menjadi bagian-bagian yang identik. Dengan bagian-bagian ini, Anda dapat mengukur bagian segmen yang lebih besar yang tidak diukur oleh seluruh segmen yang lebih kecil. Tetapi kemudian muncul bagian baru dari segmen yang lebih besar, yang tidak lagi dapat diukur oleh bagian yang dipilih. Kami menerapkan rekursi dan sekali lagi memecah bagian yang sudah rusak menjadi komponen yang lebih kecil. Kami mengukurnya sebelumnya tak terukur. Dan lagi kita mendapatkan sisa tak terukur. Bagilah bagian lagi, ukur lagi. Sekali lagi kita dapatkan sisanya. Tapi kamu bisa bosan!
Akibatnya, orang-orang muncul dengan ide pembulatan dan berhenti membagi unit pengukuran. Artinya, orang menilai akurasi (mereka mengatakan itu cukup). Tetapi alam tidak memaafkan ketidakakuratan dalam pemodelan.
Bagaimana rasio dimodelkan saat ini? Mereka dimodelkan menggunakan klasifikasi bilangan pecahan. Klasifikasi adalah ini - ada bilangan bulat dan ada bilangan pecahan. Yang utuh masih tidak stabil, tetapi yang fraksional dibagi menjadi fraksi terbatas dan tak hingga. Untuk saat ini, kami juga melupakan yang terakhir. Infinite dibagi menjadi rasional dan irasional. Kami biasanya lupa tentang bagian pertama. Yang irasional dibagi menjadi aljabar dan transendental. Semuanya, tidak ada lagi pembagian. Namun untuk kejelasan, kami memberikan klasifikasi dalam bentuk gambar:
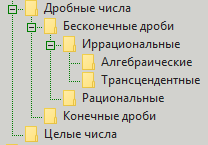
Mengapa klasifikasi ini buruk? Dia tidak terlalu buruk. Dia, seperti yang sering dikatakan oleh Winnie the Pooh, baik, tetapi entah bagaimana lumpuh ... Artinya, jelas bahwa dengan akurasi ekspresi nilai-nilai, dia tidak baik-baik saja karena ketidakterbatasannya. Tapi ada sisi lain dari koin itu. Sisi ini (dalam konteks ini) disebut "dapat dibagi". Kita tidak dapat secara tepat memisahkan dua angka (satu di atas yang lain) karena kita bersandar pada ketidakterbatasan. Tetapi di sisi lain, kita tertarik pada fenomena dari dunia angka seperti kesederhanaan dan jumlah pembagi yang menghilangkan ketidakterbatasan ketika mereka muncul. Bilangan prima membentuk dasar dari seri bilangan bulat. Dan angka-angka penting ini (termasuk, misalnya, untuk kenyamanan ketika membayar layanan untuk jarak jauh) jumlahnya sangat tergantung pada operasi divisi. Dan pembagian sering memberi kita pecahan. Dan pecahan memberi kita angka pecahan. Nah, untuk bilangan pecahan, seseorang memberi kita klasifikasi sebelumnya terbatas, tak terbatas, rasional, irasional, aljabar dan transendental. Tetapi apakah klasifikasi ini memberi kita peluang untuk menemukan jawaban atas pertanyaan tentang angka? Misalnya, tentang yang sederhana yang sama? Atau fraksional? Tampaknya memberi, tetapi tidak sebanyak yang kita inginkan.
Ambil bilangan prima. Hari ini, bilangan prima maksimum pada dasarnya sedang dicari. Yaitu, mereka mengambil nomor kandidat, dan kemudian memeriksa apakah itu sederhana atau tidak. Calon mendapatkan angka hanya - jika Anda tahu metode memeriksa kesederhanaan untuk kelas nomor tertentu, maka di sini adalah daftar kandidat dalam bentuk perwakilan kelas, yang mereka lakukan secara bodoh berturut-turut, memeriksa setiap angka, memulai setiap angka, mulai, tentu saja, dengan nilai kecil. Dan sejauh ini mereka telah mencapai jumlah urutan dua hingga tingkat delapan puluh juta aneh. Ini adalah jumlah hampir dua puluh lima juta tempat desimal. Pada prinsipnya, itu terlihat mengesankan. Tetapi apa yang mencegah kita mengingat slogan "lebih tinggi, lebih jauh, lebih cepat"?
Pada dasarnya, kita terhalang oleh kurangnya pemahaman. Ya, model kami tentang fenomena yang disebut "angka" tidak lengkap. Dan ya, bagian dari model, yang disebut "divisi", tidak lengkap ke tingkat terbesar. Oleh karena itu, delapan puluh juta unit dalam memori komputer adalah batas untuk kemanusiaan. Mengapa unit? Karena sepertinya bilangan prima terbesar. Ini adalah satu unit, tetapi dalam notasi biner. Bagi mereka, ada tes Luc-Lemer, yang menunjukkan kepada kita sejumlah sederhana atau gabungan. Dan tes ini membutuhkan tahun kerja dari satu inti prosesor untuk memeriksa satu nomor kandidat delapan puluh juta unit biner. Hanya delapan puluh megabita, atau sepuluh megabita, dan manusia tidak lagi bisa melangkah lebih jauh. Apa itu sepuluh megabyte? Ini satu sen, ini sedikit, hampir tidak ada artinya untuk komputer modern. Tetapi tes ini telah berlangsung selama bertahun-tahun. Oleh karena itu, Anda harus menjalankannya di jutaan komputer tempat sukarelawan menginstal program yang sesuai, dan sebagai hasilnya periksa satu nomor kandidat selama beberapa detik (dan ini jika ada banyak sukarelawan). Tetapi masalahnya adalah bahwa ada banyak nomor kandidat, dan karena itu butuh berbulan-bulan untuk menemukan nomor utama berikutnya. Dan dengan pertimbangan seperti itu, orang dapat berharap bahwa pergerakan hanya hingga ratusan juta unit biner akan memakan waktu sepuluh tahun.
Apakah mungkin mempercepat proses? Kamu bisa. Namun dibutuhkan lebih banyak pemahaman. Misalnya - bagaimana cara mengurangi waktu untuk menguji setiap angka? Sejauh ini, penurunan tersebut dicapai dengan memijat besi. Atau opsi kedua - Anda dapat menawarkan tes kesederhanaan yang lebih cepat. Tetapi dengan ini selama sekitar 100 tahun, sedikit yang berubah. Namun, jika Anda mengetahuinya, maka mungkin itu akan berhasil bersama kami. Hanya perlu memahami dari dasar-dasarnya.
Bintang dekat
Berpikir tentang hubungan, semua orang dapat berkontribusi banyak bagi sains. Rasa ingin tahu saja sudah cukup. Sebagai contoh, orang mungkin bertanya, mengapa klasifikasi angka fraksional begitu saja? Dan temukan jawabannya dalam eksperimen pikiran untuk mengukur rasio segmen yang sama. Pertama, segmen dikorelasikan sebagai 1 hingga 2. Rasio ini dapat dimengerti, memberi kita angka 2, yang menunjukkan berapa kali segmen yang lebih besar melebihi yang lebih kecil. Dan sekarang mari kita perpanjang segmen yang sedikit lebih kecil. Apa yang akan terjadi Rasio akan berhenti menjadi utuh. Kelebihan yang diperoleh dari pemanjangan mencegah kita mendapatkan jawaban sederhana dalam masalah. Tapi kita bisa menggunakannya sebagai penggaris. Jika cocok dengan bilangan bulat kali dalam setengah segmen yang lebih besar, maka kita dapat mengekspresikan rasio melalui bilangan bulat ini. Jadi kami mendapatkan rasio:
(1+1/N)/2
di mana N adalah berapa kali yang dibutuhkan untuk menyesuaikan kelebihan dari peregangan panjang yang lebih kecil menjadi setengah dari panjang yang lebih besar. Jadi kami mendapat nomor rasional. Itu selalu diberikan oleh rasio bilangan bulat. Jika sekarang kita memperpanjang segmen yang lebih kecil sedikit lebih banyak, maka kita bisa mendapatkan situasi di mana tidak peduli berapa banyak kita mengalikan segmen yang lebih kecil dengan bilangan bulat tertentu, kita tidak bisa mendapatkan kecocokan yang tepat dengan jumlah panjang tertentu dari segmen yang lebih besar. Jadi kami mendapat angka irasional yang mencirikan rasio baru. Perhatikan bahwa pergeseran mikroskopis dari batas segmen mengarah ke proses tak berujung untuk mengidentifikasi rasio panjang. Satu langkah untuk peneliti yang rendah hati dan perubahan besar untuk teori bilangan - elemen baru dalam klasifikasi diperlukan. Satu langkah dan - dari hak ukuran mikro hingga tak terbatas. Dari satu kategori angka ke yang benar-benar baru, pada dasarnya tidak kompatibel dengan yang sebelumnya. Bukankah itu bintang?
Namun faktanya, kami hanya sedikit mengubah satu segmen. Jadi dari mana datangnya kategori baru yang fundamental? Secara umum, klasifikasi penting karena kemampuannya untuk mencocokkan kenyataan dengan tepat. Tetapi akurasi seperti apa yang muncul bersama dengan bilangan irasional? Mereka memungkinkan Anda untuk memodelkan rasio apa pun, dan bukan hanya rasio bilangan bulat, sehingga sangat masuk akal untuk memisahkan kelas tersebut. Tapi ini tidak semua akurat, karena saya ingin memahami semua ketidakterbatasan ini, bagaimana mereka muncul, apa artinya dan mengapa mereka ada sama sekali. Benar, dengan ketidakterbatasan, semuanya tidak mudah, tetapi karena untuk saat ini kita akan berurusan dengan hubungan yang terbatas. Tampaknya semuanya sederhana dengan mereka, ambil N, bagi dengan M, dan dapatkan angka pecahan. Akan sangat baik jika jumlahnya ternyata pendek, misalnya 2,5 atau 3,25. Tetapi yang lebih sering ke dunia adalah hubungan dalam bentuk 4.12 (3456), yaitu, sekali lagi dengan ketidakterbatasan, tetapi ini adalah ketidakterbatasan “dalam periode”. Hanya memperhatikan angka yang diulang, Anda dapat dengan mudah dan kompak merekam angka dari jumlah karakter yang tak terbatas. Begitulah cara kami terkenal mengatasi ketidakterbatasan. Juga tanda bintang kecil. Tapi ini hanya pandangan sekilas.
Sekarang mari kita menghidupkan rasa ingin tahu dan mengajukan pertanyaan. Dan mengapa beberapa bilangan pecahan terbatas dan yang lainnya tak terbatas? Dan mengapa beberapa jenis yang tak terhingga panjangnya panjang, sementara yang lain dengan suatu periode? Dan mengapa sebelum periode dalam angka 4.12 (3456) kita melihat angka 1 dan 2? Dan mengapa ada persiapan? Dan mengapa pada periode itu kita melihat angka 3 dan 4? Dan mengapa panjang periode dalam contoh ini sama dengan empat? Dan mengapa jumlah angka sebelum periode sama dengan dua? Dan kita hanya melihat dengan penasaran hanya pada satu angka pecahan. Dan untuk nomor lain, pertanyaannya akan lebih menarik.
Mari kita coba jawab. Mengapa angka fraksional terbatas? Sangat sederhana - pada kenyataannya, ini adalah "ilusi optik." Lebih tepatnya - kami menggunakan satu trik. Misalnya, untuk mendapatkan angka 2.5, Anda dapat membagi 5 dengan 2. Dan untuk ini, kita semua di sekolah mengajarkan metode membagi "sudut". Tapi mari kita lihat lebih dekat metode ini. Dan kemudian kita menemukan bahwa fakir bertindak sebagai berikut - itu mengalikan dividen dengan konstanta yang mengandung pembagi, atau faktor-faktornya. Dan kemudian mengurangi persis faktor dari konstanta ke faktor pembagi. Ini terlihat seperti ini:
5/2=2+1/2=2+(1∗10/2)/10=2+1∗5/10=2,5
Itu semua mukjizat - sebuah deuce dari pembagi dikurangi menjadi deuce dari sebuah konstanta
10 yang sama dengan
5∗2 , dan satu lima tetap sebagai hasilnya, yang ditulis setelah pemisah desimal. Jumlahnya adalah
1 tidak pernah dibagikan
2 , itu dikalikan dengan
0,5 dari jumlah tersebut
2+1∗0,5 . Tetapi kami tidak melihatnya, berkat "ilusi optis" yang kami latih dari sekolah untuk diciptakan secara mandiri selama setiap operasi divisi divisi. Yah, bukankah itu bintang? Kita hanya perlu mendorong dedaunan di atas representasi bisu dari waktu sekolah dasar, ketika kita melihat cahaya dari sesuatu yang baru, tidak cukup biasa, yang tidak diajarkan di sekolah (tetapi sia-sia).
Mari kita jelaskan "ilusi optik" pada tingkat yang sedikit lebih tinggi. Kami hanya menerjemahkan hasil divisi ke dalam format yang nyaman untuk penyimpanan dan persepsi. Angka itu sendiri tidak tergantung pada format. Dan jumlah karakter di dalamnya juga. Kita telah melihat kemungkinan menempatkan tanda kurung di sekitar periode, dan dengan demikian mengurangi tak hingga panjang periode dan dua tanda kurung. Dan ini juga merupakan format data, tetapi digunakan untuk fraksi berkala. Dan format fraksi terbatas menyembunyikan tak terhingga dengan mengurangi faktor dari dasar sistem bilangan desimal. Jika kita mengambil, misalnya, sistem bilangan terner, maka pembagian 5 dengan 2 akan terlihat seperti ini:
5/2=2+1/2=2+(1∗3/2)/3=2+(1+1/2)/3=2+(1+(1∗3/2)/3)/3=
= 2 + ( 1 + ( 1 + 1 / 2 ) / 3 ) / 3 = . . . = 2.1 ( 1 )
Artinya, kita mendapat tak terbatas dalam bentuk fraksi periodik, karena sekarang kita menggunakan konstanta lain yang tidak mengandung faktor yang dapat dikurangi dengan angka 2. Tetapi dalam sistem heksadesimal, hasilnya akan kembali menjadi final - 2.3. Tetapi angka itu sendiri tetap berada di tempat yang teduh, dan mungkin rekor terbaik untuk itu adalah 5/2, dan yang lainnya adalah masalah memilih format presentasi untuk nomor ini.
Sekarang tentang pecahan tak hingga. Yang periodik diperoleh dengan membagi bilangan bulat, dan yang irasional (dengan panjang periode tak terbatas) diperoleh dengan menghitung akar beberapa derajat dari bilangan bulat. Artinya, orang memperoleh dua kategori pembagian dari abstraksi bilangan bulat - dengan faktor yang berbeda dan dengan yang sama. Opsi pertama memungkinkan Anda untuk membagi bilangan bulat apa pun menjadi bilangan bulat lainnya, tetapi kadang-kadang memberikan hasil fraksional. Opsi kedua memungkinkan Anda untuk membagi angka hanya menjadi angka-angka yang persis sama dengan hasil pembagian (termasuk beberapa untuk akar derajat besar). Secara umum, kami memiliki divisi yang sama, tetapi tanpa batasan pada hasilnya dan dengan batasan. Pembatasan membawa kita ke dua opsi: baik mengurangi pembagi dengan faktor dari dividen (dan kemudian Anda bisa mendapatkan bilangan bulat sama dengan pembagi), atau membagi dividen yang tidak dapat direduksi dengan angka tertentu. Lalu apa yang bisa menjadi "angka tertentu"? Jika bilangan bulat, maka sebagai hasilnya kita mendapatkan sebagian (dividen dan pembagi tidak dapat direduksi), yang tidak sama dengan bilangan bulat. Karena itu, karena bilangan bulat tidak cocok, Anda perlu mencari fraksi yang akan sama dengan hasilnya. Fraksi terbatas juga menghilang, karena mereka sebenarnya mewakili sejumlah bentuk
T / M yang, ketika dikalikan dengan dirinya sendiri, akan memberi kita sebagian kecil dari formulir
N ∗ N / ( M ∗ M ) , yang lagi-lagi memberi kita fraksi terbatas atau periodik, dan bukan bilangan bulat. Oleh karena itu, perlu untuk memilih fraksi yang akan mengurangi rasio kuadrat mereka ke bilangan bulat dengan pertumbuhan tak terbatas N dan M. Mengapa untuk bilangan bulat tak terbatas rasionya
N ∗ N / ( M ∗ M ) dapat dibuat utuh, tetapi tidak untuk akhirnya? Karena semakin banyak angka, semakin sedikit pengaruh pada hasilnya adalah keleluasaan mereka. Integer yang mengikuti salah satu yang dipilih tentu berbeda dari itu oleh satu. Dan unit ini tidak memungkinkan Anda untuk secara tepat mengatur hasil yang diinginkan, karena, misalnya, antara 1/1000 dan 2/1000 ada banyak angka tak terhingga, misalnya 11/10000 atau 145/100000, dll. Oleh karena itu, dengan menambah panjang angka, dimungkinkan hingga tak terbatas untuk mendapatkan hasil apa pun dengan akurasi apa pun. Dan kemudian gandakan dengan sendirinya dan dapatkan bilangan bulat.
Dan pada saat yang sama, periode pecahan seperti itu benar-benar menjadi tak terbatas, seperti yang akan kita lihat nanti. Dan periode tak terbatas adalah milik bilangan irasional, yang telah kita lewati dari bilangan rasional sepenuhnya. Inilah cahaya bintang, yang dengan mulus berubah menjadi kegelapan tak terbatas.Tetapi mengapa kita membutuhkan persimpangan antara dua kelas angka ini? Mungkin satu sudah cukup? Mari kita coba simulasikan. Jadi kami mendapatkan persis akar bilangan bulat, kami menemukan dua bilangan bulat besar yang cenderung tak terhingga, yang, ketika dikuadratkan dan dibagi satu sama lain, memberikan bilangan bulat. Sekarang tambahkan satu ke salah satu dari jumlah yang sangat besar ini. Lalu apa yang akan terjadi? Dalam bahasa kami yang biasa, kami mendapat definisi untuk nomor baru, yang tidak periodik (karena memiliki periode tak terbatas) dan pada saat yang sama bukan akar dari keseluruhan. Artinya, nomor baru tidak sesuai dengan klasifikasi yang diberikan kepada kita dari angka rasional dan irasional. Dan sekarang semua angka seperti itu dipanggil oleh ahli matematika transendental, karena Anda harus meletakkannya di suatu tempat. Tapi poin yang menarik - pada awalnya ada akar bilangan bulat, yang disebut bilangan irasional,dan kemudian angka "lainnya" muncul. Pertama-tama, demi tradisi Yunani kuno, perkiraan yang terlalu tinggi akan pentingnya bilangan bulat semuanya diklasifikasi secara tepat berdasarkan metode perolehan dari bilangan bulat. Metode pertama adalah pembagian dan bilangan rasional diturunkan darinya. Lalu orang bertemu dengan akar. Jadi ada bilangan irasional. Dan selain rasional dan irasional, kategori ketiga muncul. Selain itu, kategori ketiga pada awalnya adalah kelangkaan mengerikan yang Euler temukan, tetapi selain penemuan Euler, tidak ada yang lain seperti itu. Dan diputuskan untuk membagi irasional menjadi dua kelas - aljabar (yaitu, tumbuh dari akar) dan transendental (khusus, luar biasa, melampaui, karena hanya Euler yang dapat menemukannya). Tetapi kemudian, angka-angka yang tidak berasal dari akar menjadi masif, dan matematikawan bahkan menentukan bahwa ada lebih banyak lagi,dari aljabar. Karena itu, transendensi (ciri) dari angka-angka semacam itu hanya menjadi penghormatan kepada tradisi. Meskipun jika kita mengingat konsep korelasi, maka semua yang rasional, irasional, aljabar, dan transendental ini segera menjadi nama artifisial untuk pembagian angka yang sangat kondisional yang dihasilkan dari pergeseran sederhana dari ujung salah satu segmen yang dibandingkan. Nah, dengan pendekatan seperti itu, bilangan transendental menjadi sekadar "sisanya", yaitu, jika dari hubungan segmen, demi mempertahankan tradisi mengekstraksi bilangan bulat, kami memilih kelas yang diperoleh dengan operasi membagi dan mengekstrak akar dari bilangan bulat, kami hanya mendapatkan rasional dan aljabar, tetapi semua sisanya bersifat transendental. Artinya, secara total hanya ada tiga kategori fraksi tak hingga. Oleh karena itu, nama "transendental" menjadi agak tegang,tidakkah kamu menemukan Baiklah, baiklah, karena tradisi adalah segalanya bagi kita, bahkan dalam ilmu pasti seperti matematika.Itu saja untuk saat ini. Dalam seri berikutnya, mari kita bicara tentang bintang rasional.