Cara mewarnai polinomial dengan benar

Polinomial bukan hanya latihan dalam hal-hal abstrak. Mereka sangat bagus untuk mendeteksi struktur di tempat yang tak terduga.

Pada 2015, mantan penyair yang menjadi ahli matematika, Jun Ho membantu menyelesaikan masalah yang dirumuskan sekitar 50 tahun yang lalu. Itu dikaitkan dengan objek matematika yang kompleks, " matroids ", dan grafik (kombinasi titik dan segmen). Dan itu juga terhubung dengan polinomial - ekspresi yang kita kenal dari pelajaran matematika, yang terdiri dari jumlah variabel yang dinaikkan ke berbagai derajat.

Di beberapa titik di sekolah, Anda mungkin melewati kurung di polinomial. Misalnya, Anda mungkin ingat bahwa x ² + 2xy + y ² = (x + y) ² . Trik aljabar yang nyaman, tetapi di mana itu bisa berguna? Ternyata polinomial sangat membantu mengungkapkan struktur tersembunyi - dan Ho secara aktif menggunakan fakta ini sebagai buktinya. Berikut ini adalah teka-teki sederhana yang menggambarkan hal ini.

Misalkan kita perlu menempatkan dua tim pemain di meja persegi. Untuk mencegah penipuan, Anda harus memastikan bahwa pemain tidak duduk di sebelah pemain lain di tim mereka. Ada berapa metode tempat duduk?

Mari kita mulai dengan tempat duduk tim merah dan biru. Katakanlah pemain merah duduk di bagian atas grafik:



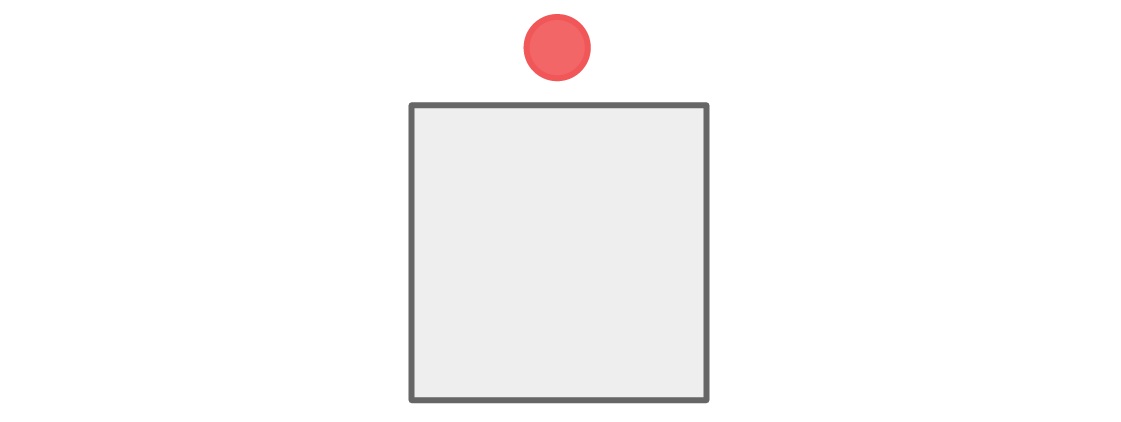
Ada dua tempat di dekat tempat teratas - kanan dan kiri - dan untuk memenuhi aturan, tempat-tempat ini harus ditempati oleh pemain biru.



Ruang di bawah ini berbatasan dengan dua yang biru, jadi pemain merah harus duduk di sana.



Tidak ada pemain yang duduk di sebelah anggota tim mereka, dan kondisi kami terpenuhi.

Kami juga bisa mulai dengan pemain biru di atas. Pertimbangan serupa mengarah pada pengaturan berikut:



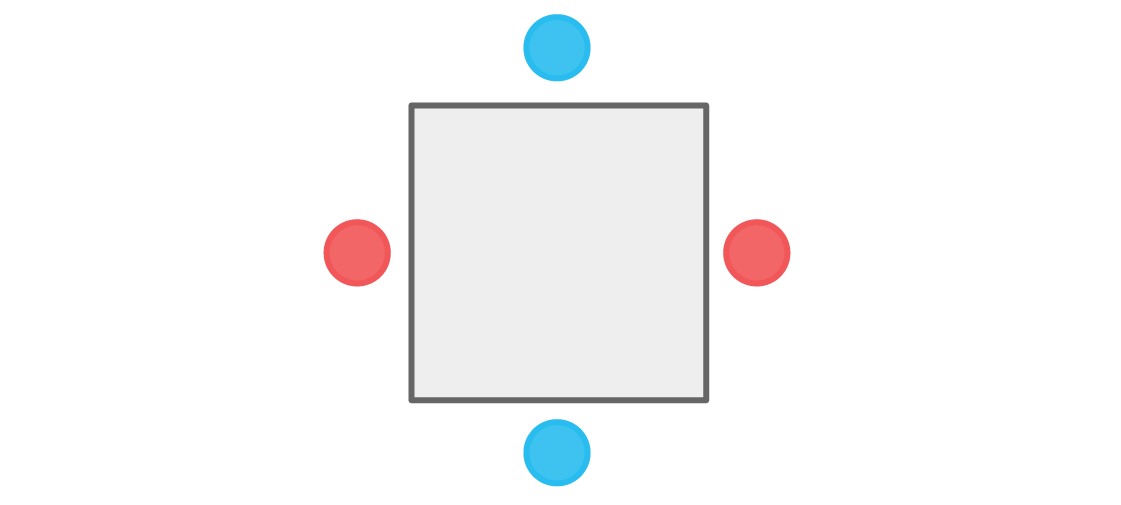
Sekali lagi, tidak ada pemain yang duduk di sebelah anggota tim lainnya. Kondisi kami terpenuhi, dan pengaturan tempat duduk seperti itu dapat diterima. Bahkan, sebenarnya ada dua pengaturan tempat duduk seperti itu. Segera setelah kami memilih warna tempat teratas, semua sisanya sepenuhnya ditentukan.

Ada cara untuk mengetahui bahwa hanya ada dua pengaturan tempat duduk yang mungkin tanpa menggambar semua diagram ini. Mari kita mulai dari atas: kita memiliki dua opsi, merah dan biru. Setelah pilihan ini, masih ada satu opsi (warna berbeda) untuk kursi kiri dan kanan. Dan untuk kursi bawah hanya ada satu opsi yang tersisa - warna yang kami mulai. Menggunakan "prinsip dasar perhitungan", kita tahu bahwa jumlah total peluang adalah hasil dari mengalikan jumlah peluang untuk setiap opsi. Ini memberi kita 2 × 1 × 1 × 1 = 2 bibit, seperti yang kita tentukan dari diagram kita.

Sekarang tambahkan perintah ketiga dengan warna ketiga. Bayangkan kita memiliki pemain merah, biru dan kuning. Berapa banyak pengaturan tempat duduk yang bisa dibuat, asalkan tempat-tempat tetangga harus memiliki warna yang berbeda? Untuk gambar semua kemungkinan, Anda harus menggambar seluruh diagram, jadi mari kita coba membuat perhitungan.

Untuk posisi teratas, kami sekarang memiliki tiga pilihan warna. Setelah pilihan ini, kita dapat memilih salah satu dari dua warna yang tersisa untuk tempat kiri dan kanan.

Apa yang akan ada di bawah alun-alun? Ada godaan untuk menyatakan bahwa untuk kursi terakhir hanya akan ada satu pilihan, karena itu di sebelah kursi kiri dan kanan. Tetapi apakah Anda merasa cacat dalam logika ini?



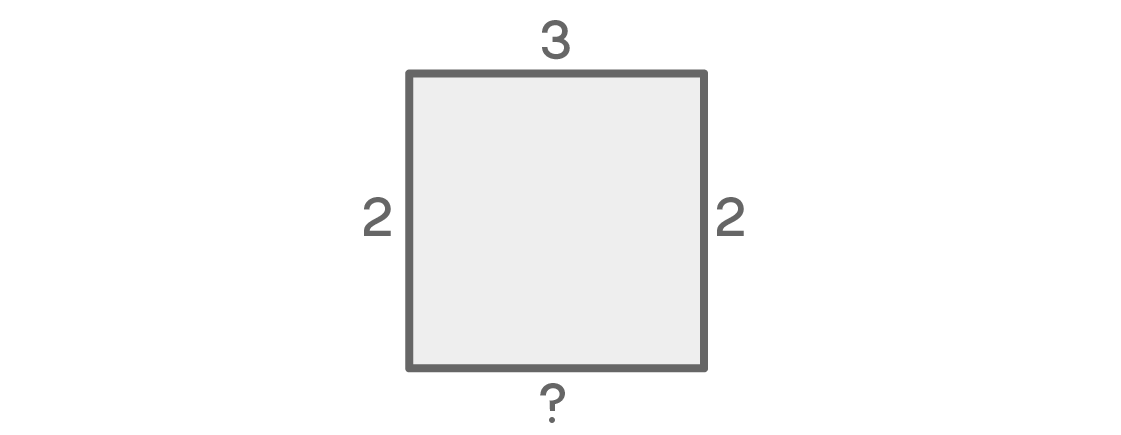
Memang, jika tempat kiri dan kanan memiliki warna yang berbeda, maka untuk tempat bawah hanya akan ada satu pilihan. Jika di sebelah kiri, misalnya, warnanya biru dan di kanan adalah merah, maka bagian bawahnya harus kuning. Tapi bagaimana jika warna kiri dan kanan sama? Dalam hal ini, untuk tempat paling bawah akan ada pilihan dua opsi. Pilihan terakhir ini tergantung pada yang sebelumnya, yang mempersulit perhitungan kami.

Kita harus mempertimbangkan dua kasus berbeda: ketika warna di kiri dan di kanan bertepatan, dan ketika mereka berbeda.

Jika warna di kiri dan kanan bersamaan, jumlah kemungkinan untuk masing-masing tempat terlihat seperti ini:



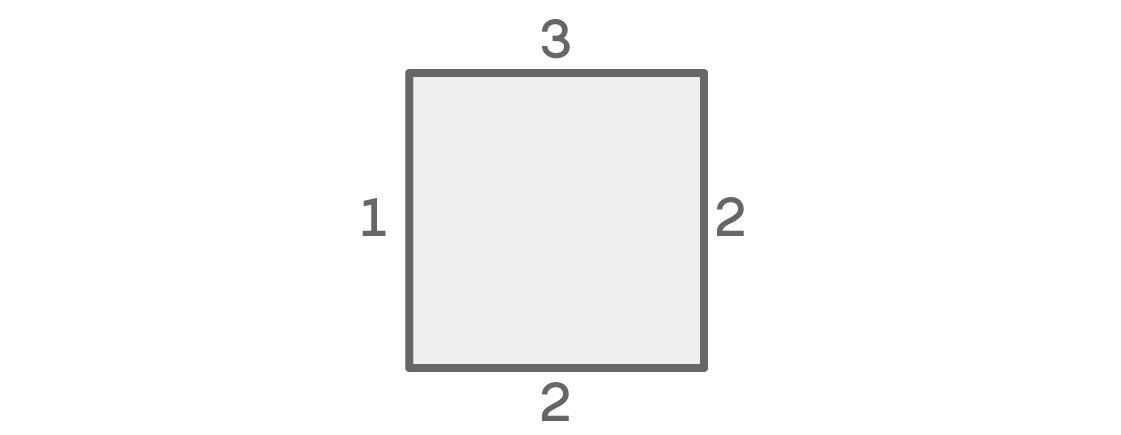
Untuk kursi atas, kami memiliki tiga pilihan. Ada dua kiri untuk kanan. Karena kami menganggap bahwa tempat kiri dan kanan memiliki warna yang sama, kami hanya memiliki satu opsi untuk tempat kiri: warna yang sama dengan kanan. Akhirnya, karena warnanya sama di kiri dan kanan, kita dapat memilih salah satu dari dua warna yang tersisa untuk kursi bawah. Hasilnya, kami mendapatkan 3 × 2 × 1 × 2 = 12 kemungkinan pengaturan tempat duduk.

Sekarang mari kita lihat kemungkinan itu ketika warna di kanan dan kiri berbeda:



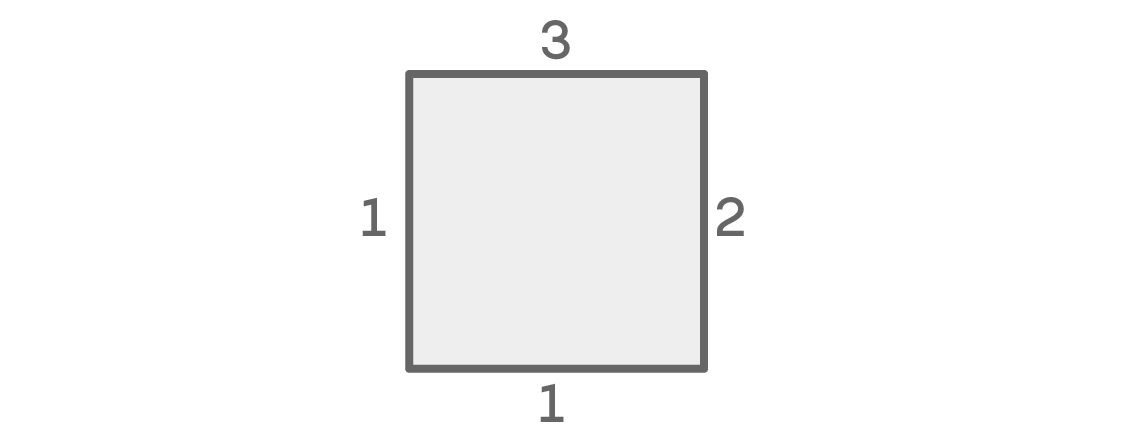
Kami lagi memiliki tiga opsi untuk bagian atas dan dua untuk tempat yang tepat. Tempat kiri lagi memiliki satu opsi, tetapi untuk alasan yang berbeda: tidak boleh sama dengan atas, tetangga, dan tidak bisa sama dengan kanan, sesuai dengan kondisi kita. Dan, karena warna di kanan dan kiri berbeda, hanya ada satu opsi yang tersisa untuk bagian bawah (sama seperti bagian atas). Kasing ini memberikan 3 × 2 × 1 × 1 = 6 kemungkinan pengaturan.

Karena kedua opsi ini mencakup semua kemungkinan, kami menambahkannya dan mendapatkan 12 + 6 = 18 kemungkinan pengaturan tempat duduk.

Menambahkan warna ketiga mempersulit tugas kita, tetapi kerja keras kita akan dihargai. Sekarang kita dapat menggunakan strategi ini untuk 4, 5 atau sejumlah q dengan warna berbeda.

Terlepas dari jumlah warna, kami akan selalu memiliki dua case: kiri dan kanan akan menjadi warna yang sama atau berbeda. Misalkan kita memiliki pilihan warna q. Berikut adalah bagan yang menunjukkan jumlah opsi untuk setiap sisi, dalam kasus di mana warna kanan dan kiri sama:



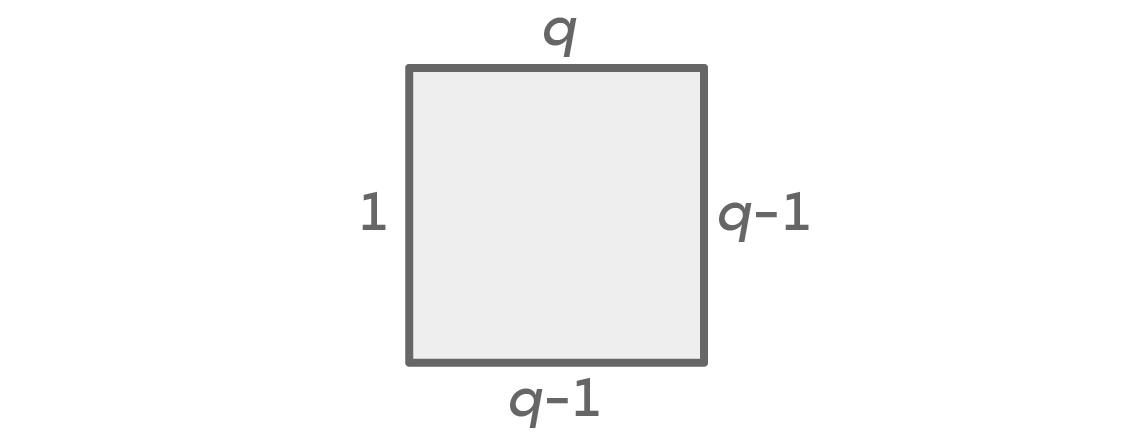
Pertama kita memiliki warna q untuk kursi atas, dan q-1 untuk kanan. Karena kami berasumsi bahwa warna di kiri dan kanan sama, kami hanya memiliki satu opsi untuk warna kiri. Ini menyisakan opsi q-1 untuk titik bawah, karena itu bisa berupa warna apa pun selain yang kita pilih untuk titik kiri dan kanan. Prinsip dasar perhitungan memberi kita q × (q - 1) × 1 × (q - 1) = q (q - 1) ² kemungkinan tata letak.

Jika tempat kiri dan kanan diwarnai berbeda, maka kita dapat menghitung kemungkinan seperti ini:



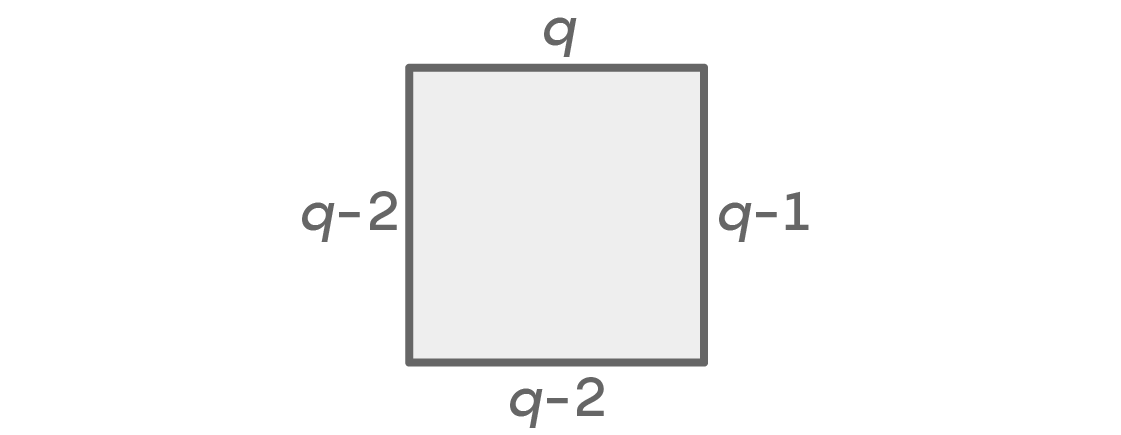
Sekali lagi, kami memiliki opsi q untuk bagian atas dan q-1 untuk tempat yang tepat. Tidak boleh ada warna yang sama di kiri yang dipilih untuk tempat atas dan kanan, jadi ada opsi q-2. Bisa ada warna di bawah ini, kecuali untuk dua yang kami gunakan kiri dan kanan, yang lagi-lagi memberikan opsi q-2. Kita mendapatkan jumlah q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² kemungkinan pengaturan tempat duduk. Karena kedua situasi ini mencakup semua opsi, kami, seperti sebelumnya, menambahkannya dan mendapatkan jumlah total pengaturan yang mungkin: q (q - 1) ² + q (q - 1) (q - 2) ² .

Ekspresi seperti itu mungkin tampak seperti jawaban aneh untuk pertanyaan: "Berapa banyak pengaturan tempat duduk yang berbeda untuk tim yang berbeda di meja persegi, sehingga dua anggota tim yang sama tidak akan duduk berdampingan?" Namun, polinomial ini mengandung banyak informasi tentang masalah kita. Dia tidak hanya memberi kita jawaban kuantitatif, tetapi juga mengungkapkan struktur tugas kita.

Polinomial semacam itu disebut " polinomial kromatik " karena ia menjawab pertanyaan: berapa banyak metode yang ada untuk mewarnai simpul-simpul jaringan (atau grafik) sedemikian rupa sehingga setiap pasangan simpul yang bertetangga memiliki warna yang berbeda?

Awalnya, masalah kami terkait dengan tempat duduk di sekitar meja, tetapi kita dapat dengan mudah mengubahnya menjadi pertanyaan tentang mewarnai simpul grafik. Alih-alih orang di meja:



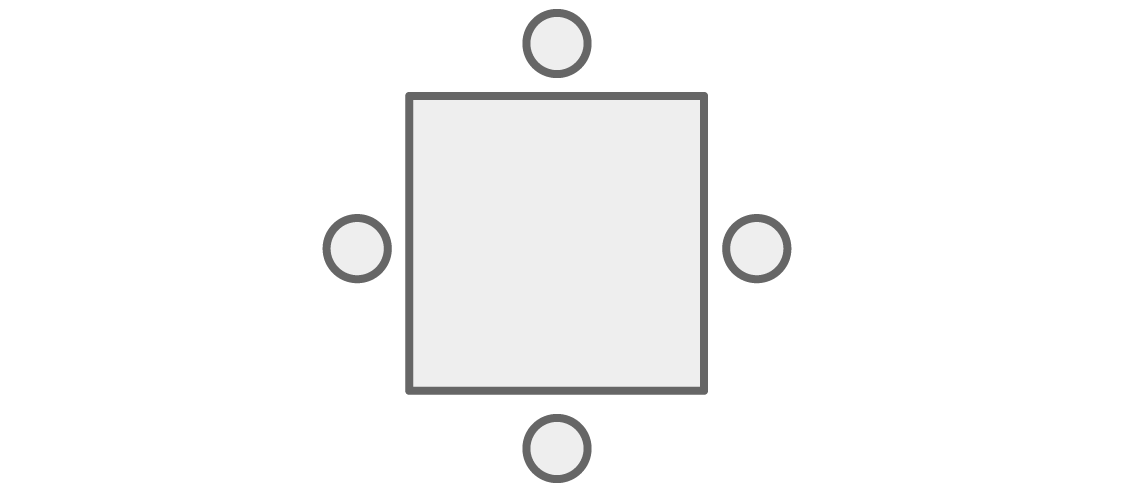
kita akan membayangkannya dalam bentuk puncak yang dihubungkan oleh tepian dalam kasing ketika mereka duduk di sebelah:



Sekarang, setiap pewarnaan dari simpul grafik dapat direpresentasikan sebagai tempat duduk orang-orang di sekitar alun-alun, di mana "duduk di sebelah" di meja berarti "memiliki tepi yang sama" pada grafik.

Sekarang, setelah merumuskan kembali masalah kita dalam bentuk grafik, kita kembali ke polinomial berwarna. Kami menyebutnya P (q).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

Sifat luar biasa dari polinomial ini adalah ia menjawab pertanyaan pewarnaan untuk jumlah warna yang memungkinkan. Misalnya, untuk menjawab pertanyaan dengan tiga warna, kami menempatkan q = 3, dan kami mendapatkan:

P (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

Ini adalah jawaban yang kami terima dalam kasus tiga tim. Dan jika kita menempatkan q = 2:

P (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

Terdengar akrab? Ini adalah jawaban untuk teka-teki pertama kami, dengan dua tim. Kita dapat menemukan jawaban untuk empat, lima, atau bahkan 10 tim yang berbeda, cukup dengan mengganti nilai yang diinginkan untuk q: P (4) = 84, P (5) = 260, dan P (10) = 6 570. Polinom kromatik menangkap beberapa struktur dasar masalah. dengan merangkum strategi penghitungan kami.

Kita dapat mengungkapkan lebih detail struktur dengan melakukan operasi aljabar pada P polinomial kami (q) = q (q - 1) ² + q (q - 1) (q - 2) ² :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² −4q + 4)
= q (q - 1) (q ² −3q + 3)

Kami mengekstraksi faktor q (q - 1) dari setiap bagian dari jumlah dan menggabungkan istilah yang serupa, mengurangi polinomial menjadi bentuk faktor. Dan dalam bentuk ini, polinom dapat memberi tahu kita tentang struktur dengan bantuan "akarnya".

Akar polinomial adalah nilai input yang menjadi sama dengan nol pada output. Lebih mudah untuk menemukan akar dalam bentuk faktorisasi: karena polinomial dinyatakan sebagai bagian yang dikalikan, nilai apa pun yang salah satu faktornya sama dengan nol akan menyetel ulang seluruh produk.

Sebagai contoh, P polinomial kami (q) = q (q - 1) (q ² - 3q + 3) memiliki faktor (q - 1). Jika kita mengambil q = 1, faktor ini menjadi sama dengan nol, seperti seluruh hasil perkalian. Yaitu, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. Demikian pula, P (0) = 0 × (–1) × 3 = 0 Oleh karena itu, q = 1 dan q = 0 adalah akar dari polinomial kami. (Anda mungkin tertarik pada faktor (q ² - 3q + 3). Karena tidak sama dengan nol untuk q nyata, itu tidak memberikan akar baru ke polinomial kromatik kami).

Akar ini masuk akal dalam kerangka grafik kita. Jika kita memiliki pilihan warna yang sama, setiap simpul harus memiliki warna yang sama. Grafik tidak mungkin diwarnai sehingga semua simpul yang berdekatan memiliki warna yang berbeda. Inilah yang berarti bahwa q = 1 adalah akar dari polinomial kromatik kami. Jika P (1) = 0, maka ada persis nol cara untuk mewarnai grafik sehingga simpul yang bertetangga tidak berwarna sama. Hal yang sama berlaku untuk versi dengan nol jumlah warna, P (0) = 0. Akar dari polinomial kromatik kami memberi tahu kami tentang struktur grafik kami.

Kemampuan untuk melihat struktur melalui aljabar menjadi lebih jelas jika kita mempertimbangkan grafik lain. Mari kita lihat grafik segitiga:



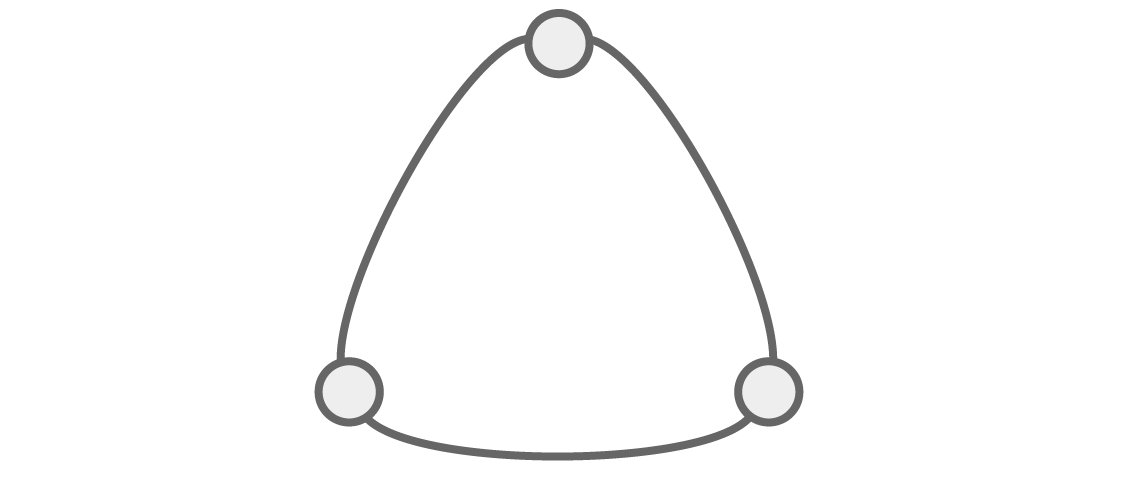
Berapa banyak cara yang ada untuk mewarnai grafik ini q dengan warna sehingga simpul yang bertetangga bukan warna yang sama?

Seperti biasa, untuk dua simpul tetangga pertama ada opsi q dan q-1. Dan karena titik terakhir berdekatan dengan dua yang pertama, itu harus berbeda dalam warna dari keduanya, yang membuat kita dengan opsi q-2. Ini memberi kita polinomial kromatik untuk grafik segitiga ini: P (q) = q (q - 1) (q - 2).

Dalam bentuk faktorisasi ini, polinomial kromatik ini memberi tahu kita sesuatu yang menarik: ia memiliki akar q = 2. Dan jika P (2) = 0, seharusnya tidak mungkin untuk mewarnai grafik ini dengan dua warna sehingga tidak memiliki dua simpul yang berdekatan dengan warna yang sama. Benarkah begitu?

Bayangkan kita sedang berjalan dalam lingkaran di segitiga ini, mewarnai puncak sepanjang jalan. Jika kita hanya memiliki dua warna, kita perlu berganti-ganti setelah setiap simpul: jika yang pertama merah, maka yang kedua akan biru, yang berarti bahwa yang ketiga lagi harus merah. Tetapi puncak pertama dan ketiga berdekatan, dan mereka tidak bisa merah keduanya. Dua warna tidak cukup, seperti prediksi polinomial.

Dengan menggunakan argumen bolak-balik yang serupa, kita dapat sampai pada generalisasi yang signifikan: polinomial kromatik dari setiap loop tertutup dengan jumlah ganjil simpul harus memiliki akar yang sama dengan 2. Karena jika Anda mengganti dua warna dan bergerak di sepanjang loop dengan panjang ganjil, simpul berwarna pertama dan terakhir akan menjadi warna yang sama . Tapi sama seperti ini adalah lingkaran, mereka akan berdekatan. Pewarnaan tidak dimungkinkan.

Sebagai contoh, kita dapat menggunakan berbagai teknik untuk menentukan bahwa untuk loop dengan lima simpul polinomial kromatik terlihat seperti ini: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. Dengan memperhitungkan ini, kita mendapatkan P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). Seperti yang diharapkan, ternyata q = 2 adalah root, dan P (2) = 0. Menariknya, begitu kita menemukan hubungan antara grafik dan polinomialnya, ide-ide mulai bekerja di kedua arah. Polinomial dapat memberi tahu kita informasi tentang struktur grafik, dan grafik dapat memberi tahu kita tentang struktur polinomial.

Pencarian struktur inilah yang membuat Ho Juni membuktikan hipotesis 40 tahun Reed mengenai polinomial kromatik. Hipotesis menyatakan bahwa jika kita menghitung koefisien polinomial kromatik dalam rangka, mengabaikan tanda-tanda mereka, kondisi berikut akan terpenuhi: kuadrat dari koefisien apa pun harus setidaknya produk dari dua yang bertetangga. Misalnya, dalam polinomial kromatik untuk loop lima-simpul kami, P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q, kita melihat bahwa 5 ² ≥ 1 × 10, 10 ² ≥ 5 × 10 dan 10 ² ≥ 10 × 4. Dari sini, misalnya, berarti tidak semua polinomial dapat berwarna: polinomial kromatik yang terkait dengan grafik memiliki struktur yang lebih dalam. Selain itu, hubungan antara polinomial ini dan domain lainnya memungkinkan Ho dan rekan penulisnya untuk menjawab pertanyaan yang jauh lebih luas terkait dengan hipotesis Roth, beberapa tahun setelah bukti hipotesis Reed.

Mungkin polinomial terkenal karena bentuk terburuknya - sebagai latihan abstrak dalam manipulasi formal ekspresi aljabar. Tetapi polinomial dan sifat-sifatnya - akar, koefisien, berbagai bentuk - membantu mengungkapkan struktur di tempat-tempat tak terduga, menciptakan koneksi dengan aljabar dalam segala hal yang mengelilingi kita.

Latihan

1. Grafik lengkap adalah grafik, masing-masing pasangan simpul yang terhubung oleh suatu tepi. Temukan polinomial kromatik dari grafik lengkap lima simpul.


2. Temukan polinomial kromatik untuk grafik berikutnya (gunakan informasi tentang polinomial kromatik dari grafik yang lebih sederhana).




3. Grafik disebut dua sisi jika simpulnya dapat dibagi menjadi dua kelompok, A dan B, sehingga simpul dari A berdekatan hanya dengan simpul B, dan simpul B berdekatan hanya dengan simpul dari A. Misalkan graf G memiliki P polinomial kromatik (q). Apa properti P (q) yang memungkinkan Anda untuk menyimpulkan bahwa grafik G adalah dua sisi?