Ada banyak artikel di Internet dengan deskripsi algoritma gradient descent. Akan ada satu lagi.
Pada 8 Juli 1958, The New York Times menulis : “Seorang psikolog menunjukkan cikal bakal komputer yang dirancang untuk membaca dan menjadi lebih bijaksana. Dikembangkan oleh Angkatan Laut ... komputer $ 704, yang menelan biaya $ 2 juta, belajar untuk membedakan antara kiri dan kanan setelah lima puluh upaya ... Menurut Angkatan Laut, mereka menggunakan prinsip ini untuk membangun mesin pemikiran pertama dari kelas Perceptron, yang dapat membaca dan menulis; pengembangan direncanakan akan selesai dalam satu tahun, dengan total biaya $ 100.000 ... Para ilmuwan memperkirakan bahwa nantinya Perceptrons akan dapat mengenali orang dan memanggil mereka dengan nama, langsung menerjemahkan pidato lisan dan tertulis dari satu bahasa ke bahasa lain. Mr Rosenblatt mengatakan bahwa pada prinsipnya adalah mungkin untuk membangun "otak" yang dapat mereproduksi diri mereka sendiri di jalur perakitan dan yang akan menyadari keberadaan mereka sendiri "(dikutip dan diterjemahkan dari buku oleh S. Nikolenko," Pembelajaran mendalam, pencelupan dalam dunia jaringan saraf ").
Ah, jurnalis ini tahu bagaimana cara membuat intrik. Sangat menarik untuk mengetahui apa sebenarnya mesin berpikir dari kelas Perceptron.
Klasifikasi biner (biner) objek, neuron buatan dari kelas Perceptron
Ini adalah neuron buatan kita, ia membagi objek menjadi dua kelas (melakukan klasifikasi objek biner):

Jadi kita punya:
- Input: objek pengambilan sampel - vektor ruang m-dimensi x = ( x 1 , . . . , x m )
- Bobot w = ( w 1 , . . . , w m ) satu untuk setiap fitur objek sampel (juga vektor m-dimensi)
- Di dalam: adder S U M = w 1 x 1 + . . . + W m x m = j u m l a h m j = 1 w j x j - jumlah input neuron tertimbang
- Berikutnya: aktivasi Φ ( x , w ) = Φ ( S U M )
- Lebih jauh lagi: quantizer (threshold) - θ [theta]
- Aktivasi + ambang batas - prediksi label kelas suatu objek berdasarkan pada jumlah input neuron yang terbobot (atribut objek). Bagian ini mendefinisikan arsitektur spesifik neuron.
- Output: label kelas objek (satu dari dua) \ hat {y} = \ {1, -1 \}\ hat {y} = \ {1, -1 \}
Klasifikasi - karena neuron memberikan kelas ke objek, biner ( biner ) - karena hanya ada dua kelas yang mungkin.
haty [permainan dengan penutup] - kami akan menunjukkan nilai kelas yang diprediksi (dihitung) untuk objek x
y [permainan reguler tanpa penutup] - true (dikenal) nilai-nilai kelas untuk suatu objek x dari set pelatihan.
Nilai-nilai x (selanjutnya x dan w - ini bukan nilai satuan, tetapi vektor) bervariasi dari objek ke objek, koefisien berat w (sekali dipilih) tetap tidak berubah. Untuk set pelatihan untuk setiap objek x label kelas dikenal y . Pada tahap pelatihan, Anda harus memilih bobot w sehingga model menghasilkan nilai yang benar haty (bertepatan dengan y ) untuk jumlah objek maksimum dalam set pelatihan. Asumsi kegunaan neuron yang dilatih dengan cara ini didasarkan pada harapan bahwa itu akan menghasilkan nilai yang benar dengan koefisien yang dipilih haty untuk objek baru x nilai kelas yang benar y yang tidak diketahui sebelumnya.
Arti intuitif dari jumlah tertimbang dari input neuron adalah bahwa semua atribut dari suatu objek (masing-masing tanda adalah salah satu input dari neuron) mempengaruhi hasil klasifikasi objek, tetapi tidak semua tanda sama-sama terpengaruh. Sejauh mana - menentukan berat; memberi nol pada koefisien bobot tertentu membatalkan kontribusi atribut yang sesuai dengan jumlah total, mis. ini sama saja dengan menghapus fitur dari objek.
Adaptif Linear Neuron ADALINE
Neuron ADALINE (neuron linier adaptif) adalah neuron buatan biasa dengan fungsi aktivasi ini:
Φ(x,w)=Φ(SUM)=SUM
Phi(x(i),w)= Phi( jumlahmj=1wjx(i)j)= summj=1wjx(i)j
Selanjutnya superskrip i dalam kurung akan menunjukkan i elemen dari set pelatihan x(i) atau nilai kelas yang benar y(i) atau nilai kelas yang diprediksi haty(i) untuknya.
Kita dapat mengatakan bahwa neuron semacam itu sama sekali tidak memiliki fungsi aktivasi dan nilai jumlah input tertimbang diumpankan ke input quantizer (ambang). Tetapi untuk konsistensi, akan lebih mudah untuk mengasumsikan bahwa nilai dari jumlah tertimbang diambil sebagai aktivasi.
Threshold (quantizer) - memprediksi label kelas:
\ hat {y} ^ {(i)} = \ kiri \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x ^ {(i)}, w) <\ theta \ end {matrix} \ benar.
Jika nilai aktivasi lebih besar dari beberapa nilai ambang θ [theta], maka quantizer memberikan label “1” ke objek, jika nilai aktivasi kurang dari ambang θ, objek menerima label “-1”.
Di sini kita dapat merumuskan masalah dalam perkiraan pertama : kita perlu memilih parameter neuron
- faktor pembobotan wj,j=1,..,m
- dan ambang θ [theta]
sehingga nilai-nilai kelas haty , yang ditugaskan neuron ke objek sampel pelatihan, bertepatan dengan nilai sebenarnya dari kelas y untuk elemen yang sama (atau, setidaknya, memberi arti yang benar untuk mayoritas).
Kami mengubah fungsi ambang sedikit, mengambil kasus untuk kelas haty=1 dan mentransfer ambang ke sisi kiri ketidaksetaraan:
begincollected Phi(x(i),w) ge theta hfilljumlahmj=1wjx(i)j ge theta hfill− theta+ summj=1wjx(i)j ge0 hfill endcollected
menunjukkan w0=− theta dan x0=1
begincollectedw0x(i)0+ summj=1wjx(i)j ge0,w0=− theta,x0=1 hfilljumlahmj=0wjx(i)j ge0,x0=1 hfill endcollected
Seperti yang kita lihat, kami berhasil menyingkirkan parameter yang terpisah θ, memperkenalkannya dengan kedok koefisien bobot baru w0 di bawah tanda jumlah, sambil menambahkan ke deskripsi objek tanda unit boneka baru x0=1 .
Kami akan memperbaiki rumusan masalah dengan mempertimbangkan notasi baru.
Tugas ' : pilih parameter faktor pembobot neuron wj,j=0,..,m ,
x0=1 (tanda-konstan) - neuron fiktif ( neuron pemindahan )
Mulai dari tempat ini, kami menomori tanda dan bobot c 0, bukan 1. Tentang vektor w kita akan mengatakan bahwa ini tentang (m + 1) -dimensi, dan bukan m-dimensional. Vektor x tergantung pada konteksnya, kita dapat mempertimbangkan (m + 1) -dimensi (sebagian besar dalam rumus), tetapi ingat bahwa sebenarnya itu adalah m-dimensional.
Mengapa neuron ( dalam kasus kami, bagaimanapun, ini bukan neuron, tetapi tanda suatu objek atau hanya input, tetapi dalam kasus jaringan multilayer berubah menjadi neuron dan biasanya disebut demikian ) adalah fiktif - sudah jelas sekarang. Kenapa dia juga perpindahan akan menjadi jelas nanti.
Aktivasi dengan jumlah sekarang akan terlihat seperti ini:
Phi(x(i),w)= Phi( jumlahmj=0wjx(i)j)= summj=0wjx(i)j,x(i)0=1 foralli
Ambang sekarang selalu 0 (nol) (nilai riil dipindahkan ke parameter w0 ):
\ hat {y} ^ {(i)} = \ kiri \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^ {(i)}, w) <0 \ end {matrix} \ benar.
Sekali lagi kami merumuskan masalah dengan kata lain (makna geometris masalah)
Jika kita hati-hati melihat rumus untuk fungsi aktivasi, kita akan melihat bahwa itu adalah hyperplane parametrik dalam ruang dimensi (m + 1), sedangkan pada dimensi m pertama ia berdampingan dengan titik-titik elemen sampel, dan (m + 1) - Dimensi-e adalah ruang nilai fungsi, terpisah dari elemen.
Sekarang, jika kita menyamakan nilai aktivasi ke nol (nilai ambang batas), maka ini juga akan menjadi hyperplane, hanya sudah ada di ruang m-dimensional, mis. sepenuhnya di ruang nilai elemen x . Hyperplane ini akan memisahkan elemen. x menjadi dua kelompok terpisah.
Biasanya di tempat ini mereka mengatakan bahwa tugas kita adalah memilih nilai parameter w , yaitu buatlah sebuah hyperplane m-dimensional dalam ruang elemen sehingga elemen-elemen dari pelatihan yang ditetapkan dengan nilai sebenarnya dari kelas "1" berada di satu sisi pesawat, dan elemen dengan kelas sejati "-1" di sisi lain.
Bagi mereka yang tidak mengerti apa yang ditulis di sini, baca terus - sekarang kita semua akan melihat, ini yang pertama. Kedua, kita juga akan melihat bahwa pernyataan masalah seperti itu, meskipun valid, tidak sepenuhnya lengkap.
Ruang satu dimensi (m = 1)
Di sinilah kode mulai muncul. Kami membangun semua grafik dengan perpustakaan Matplotlib biasa, tapi di sini saya juga menggunakan perpustakaan Seaborn dalam satu baris untuk menyesuaikan area grafik, karena Saya suka bagaimana dia melakukannya, tetapi pada prinsipnya Anda dapat melakukannya tanpa dia.
Kami mengambil banyak poin 1-dimensi dan menjawabnya:
import numpy as np import math
Di sini kita memiliki setiap elemen ke-i dari array X1 - ini adalah elemen ke-i (titik ke-th) dari sampel pelatihan (lebih tepatnya, atribut 1 dan satu-satunya): x(i)=(X1[i]) , x(i)1=X1[i]
Setiap elemen ke-i dari array y adalah jawaban yang benar, label sejati yang sesuai dengan elemen ke-i dari sampel pelatihan dengan atribut tunggal X1 [i].
Kami hanya mengambil 5 poin, dua yang pertama ditugaskan ke kelas "-1", tiga sisanya ditugaskan ke kelas "1".
Gambarlah poin-poin ini di telepon:
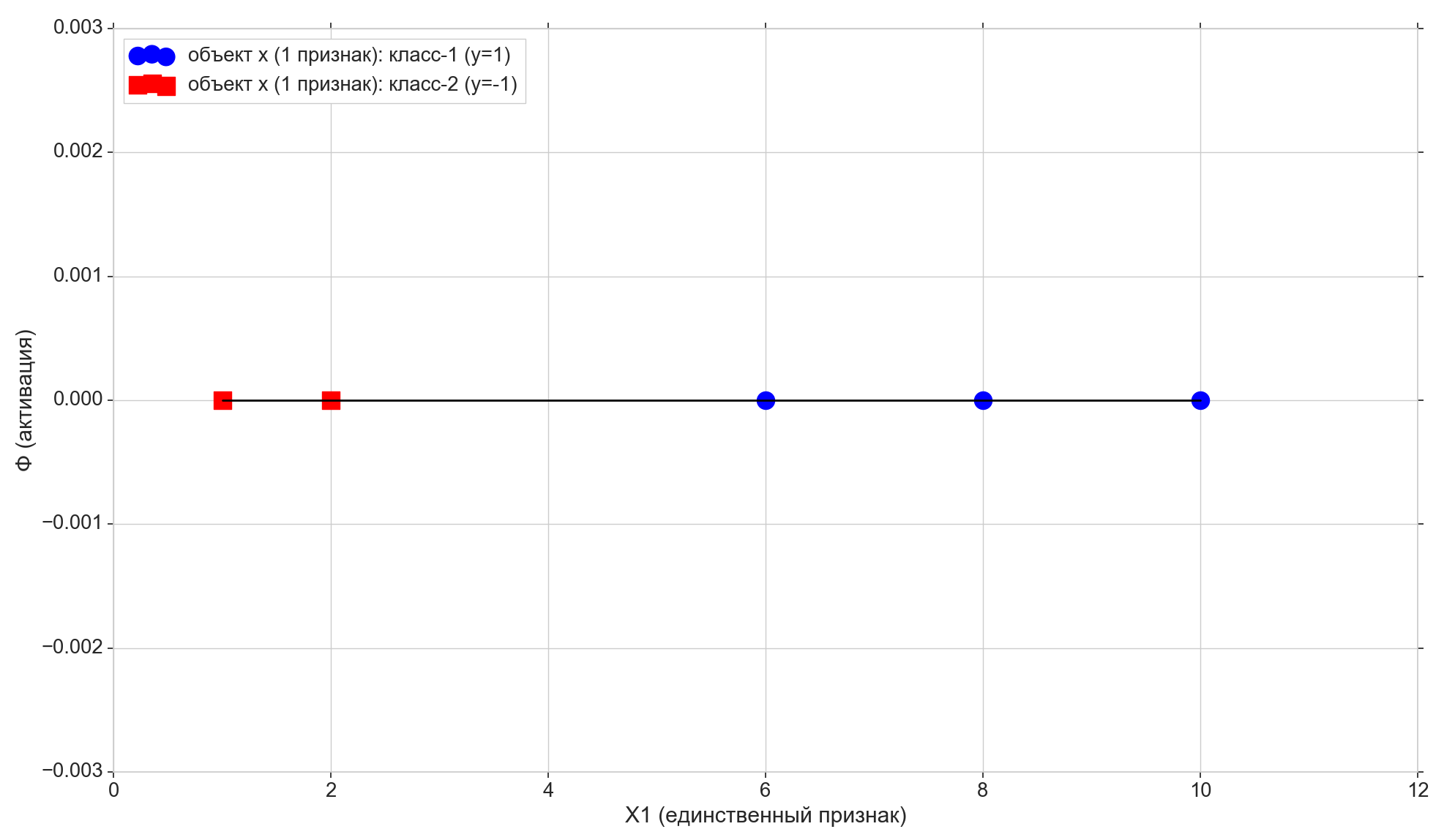
Sekarang mari kita lihat fungsi aktivasi:
Phi=w0+w1x1
Seperti yang Anda lihat, ini adalah garis parametrik biasa pada bidang (dalam 2-dimensi, mis. (M + 1) -dimensi ruang):
- pada sumbu horizontal kita memiliki titik-titik elemen (mereka juga nilai-nilai atribut X1)
- pada nilai aktivasi - vertikal untuk setiap elemen
- parameter w1 - Menetapkan sudut kemiringan,
- tapi w0 - bergeser di sepanjang sumbu vertikal (inilah jawaban untuk neuron geser ).
w0 = -1.1 w1 = 0.4

Ingat juga bahwa setelah konversi kecil, ambang aktivasi kami berubah menjadi nol. Dengan demikian, jika proyeksi elemen ke-i ke garis aktivasi lebih rendah dari nol, kami menetapkan kelas -1 ke elemen ( haty=−1 ), jika lebih tinggi dari nol, kami menetapkan kelas "1" ( haty=1 )
Titik ungu - persimpangan garis aktivasi dengan sumbu Phi=0 , memisahkan elemen dari kelas yang berbeda, ini adalah hyperplane yang sangat terpisah (untuk ruang 1-dimensi, intinya adalah hyperplane) yang dibangun dalam ruang fitur 1-dimensi (mis. m-dimensional). Seperti yang Anda lihat, untuk membagi elemen menjadi kelompok, itu sudah cukup, tetapi untuk menetapkan kelas ke grup, itu tidak lagi cukup. Untuk menetapkan kelas ke elemen, kita memerlukan aktivasi (hyperplane 2-dimensi) langsung yang dibangun dalam 2-d (yaitu, dalam (m + 1) -d) ruang "tanda + aktivasi": arah deviasi aktivasi dari vertikal sumbu akan menentukan kelas untuk kelompok elemen, karena itu tergantung pada apakah proyeksi elemen pada aktivasi lebih tinggi atau lebih rendah dari nol.
Mengubah parameter w0 dan w1 kami akan menerima jalur aktivasi yang berbeda. Kita perlu membangun jalur aktivasi seperti itu, mis. temukan kombinasi parameter seperti itu w di mana proyeksi dua poin pertama dari sampel pelatihan pada garis aktivasi di bawah nol (bagi mereka, nilainya haty=y=−1 ), dan proyeksi 3 poin sisanya akan berada di atas nol (untuk mereka haty=y=1 )
Cukup jelas bahwa dalam kasus khusus kami tidak ada yang rumit dalam membangun garis seperti itu, apalagi, garis tersebut umumnya dapat dibangun dalam jumlah tak terbatas. Tetapi kami akan mencoba membangunnya sedemikian rupa sehingga beberapa kriteria optimalitas dipenuhi (dapat mempengaruhi kualitas prediksi masa depan), ditambah harus ada kemampuan untuk memperluas algoritma ke kasus multidimensi.
Di sini kami juga mencatat bahwa kami secara khusus memilih set poin awal sehingga dapat dibagi dengan garis seperti itu (untuk 1-e: semua elemen dari kelompok pertama lebih kecil, semua elemen dari kelompok kedua lebih besar dari beberapa nilai tetap), yaitu. banyak poin pelatihan terpisah secara linear .
Tambahkan dua garis horizontal lagi ke grafik yang sesuai dengan kelas {1, -1}, dan proyeksikan elemen ke atasnya.

Poin dengan proyek "-1" kelas ke garis bawah Phi=−1 , poin dengan proyek kelas "1" ke baris teratas Phi=1 .
Mari kita perhatikan satu lagi nuansa kecil. Kami memplot nilai aktivasi sepanjang sumbu vertikal, ruang nilai aktivasi kontinu. Tetapi hasil dari classifier (fungsi aktivasi melewati ambang) adalah satu set diskrit dari dua elemen {-1, 1}, dan bukan skala kontinu. Di sini kita mengambil satu set kelas diskrit y dan letakkan pada skala aktivasi berkelanjutan Phi sehingga nilai kelas diskrit menjadi titik biasa pada skala aktivasi - kasus khusus nilai aktivasi yang dapat langsung diterima atau didekati cukup dekat dengan mereka. Sebenarnya, kita awalnya tidak dapat mengambil nilai numerik sebagai kelas, tetapi string label "class-1" dan "class-2", dalam hal ini kita harus mencocokkan label string dengan nilai numerik pada skala aktivasi. Oleh karena itu, dalam kasus kami, nilai-nilai kelas "-1" dan "1" harus diambil bukan sebagai label kelas seperti mereka, tetapi sebagai pemetaan kelas yang ditandai untuk skala aktivasi.
Saatnya untuk memasukkan metrik kesalahan

Adalah wajar untuk menerima bahwa semakin dekat nilai aktivasi untuk elemen yang dipilih adalah dengan nilai kelas untuk elemen yang sama, semakin baik prediksi kelas aktivasi untuk elemen ini. Jadi, untuk kesalahan untuk elemen yang dipilih, Anda dapat mengambil jarak antara titik - proyeksi vertikal elemen pada garis aktivasi dan proyeksi elemen pada garis horizontal dari kelas yang diketahui (benar). Pada grafik: kesalahan - garis oranye vertikal.
Fungsi biaya (kerugian)
Kami memiliki metrik kesalahan untuk setiap item individual. Kita dapat memperolehnya dari metrik kualitas untuk seluruh jalur aktivasi. Sangat wajar untuk menerima, misalnya, bahwa semakin kecil jumlah kesalahan semua elemen sampel pelatihan, semakin baik kita membangun jalur aktivasi. Untuk setiap elemen individu, kesalahannya tidak akan minimal, tetapi untuk seluruh sampel pelatihan secara keseluruhan, Anda bisa mendapatkan beberapa kompromi.
Tapi Anda bisa mengambil bukan jumlah kesalahan sederhana, tetapi jumlah kesalahan kuadrat ( jumlah kesalahan kuadrat, jumlah kesalahan kuadrat, SSE ). Sangat jelas bahwa, seperti dalam kasus jumlah kesalahan biasa, semakin dekat garis aktivasi ke titik dengan kelas elemen yang benar, semakin kecil jumlah kesalahan kuadrat, tetapi dalam kasus kesalahan kuadrat, elemen yang paling jauh akan menerima penalti yang lebih parah.
Sebenarnya, yang menarik bagi kita di sini bukanlah ukuran denda untuk elemen yang jauh, tetapi fakta bahwa fungsi kuadratik memiliki minimum dan dapat dibedakan di mana-mana (jumlah yang biasa akan memiliki minimum, tetapi pada minimum ini tidak akan dapat dibedakan), lihat mengapa ini perlu. sedikit kemudian.
Jadi:
- Kesalahan - jarak dari nilai label kelas ke hyperplane aktivasi
- SSE - jumlah kesalahan kuadrat semua elemen sampel pelatihan
- Fungsi biaya J(w) - metrik kualitas untuk jalur aktivasi yang dipilih. Semakin rendah nilainya, semakin baik aktivasi.
Ambil sebagai fungsi nilai 1 lebihdari2 SSE, dalam kasus umum untuk neuron linier, akan terlihat seperti ini:
begincollectedJ(w)=1 lebihdari2SSE=1 lebihdari2 jumlahni=1( Phi( jumlahmj=0wjx(i)j)−y(i))2=1 lebihdari2 jumlahni=1( jumlahmj=0wjx(i)j−y(i))2 endcollected
( 1 lebihdari2 di tempat pertama, itu tidak mengganggu SSE, dan, kedua, untuk kenyamanan - itu akan dikurangi dengan indah)
Di sini i - nomor elemen, dan n - jumlah elemen dalam set pelatihan. Biarkan saya mengingatkan Anda itu y(i) - kelas sejati i elemen sampel pelatihan, mis. Jawaban benar terkenal sebelumnya.
Seperti yang kita ingat, posisi jalur aktivasi ditentukan oleh parameter - faktor bobot w oleh karena itu vektor w bertindak sebagai parameter dari fungsi kerugian.
Untuk kasus 1 dimensi
J(w)=1 lebihdari2SSE=1 lebihdari2 sumni=1(w0+w1x(i)1−y(i))2
Nilai-nilai x dan y diketahui sebelumnya (ini adalah set pelatihan), oleh karena itu mereka diperbaiki. Kami memilih parameter w , yaitu w0 dan w1 sehingga nilainya J(w) Ternyata sangat minim. Mari kita coba plot grafik sebagai nilainya J(w) tergantung pada parameternya w0 dan w1

Secara umum, sudah terlihat di sini bahwa fungsi kerugian memiliki minimum, dan di mana ia berada kira-kira. Tetapi mari kita lakukan satu trik lagi dan membangun grafik yang sama, hanya dengan skala vertikal logaritmik .

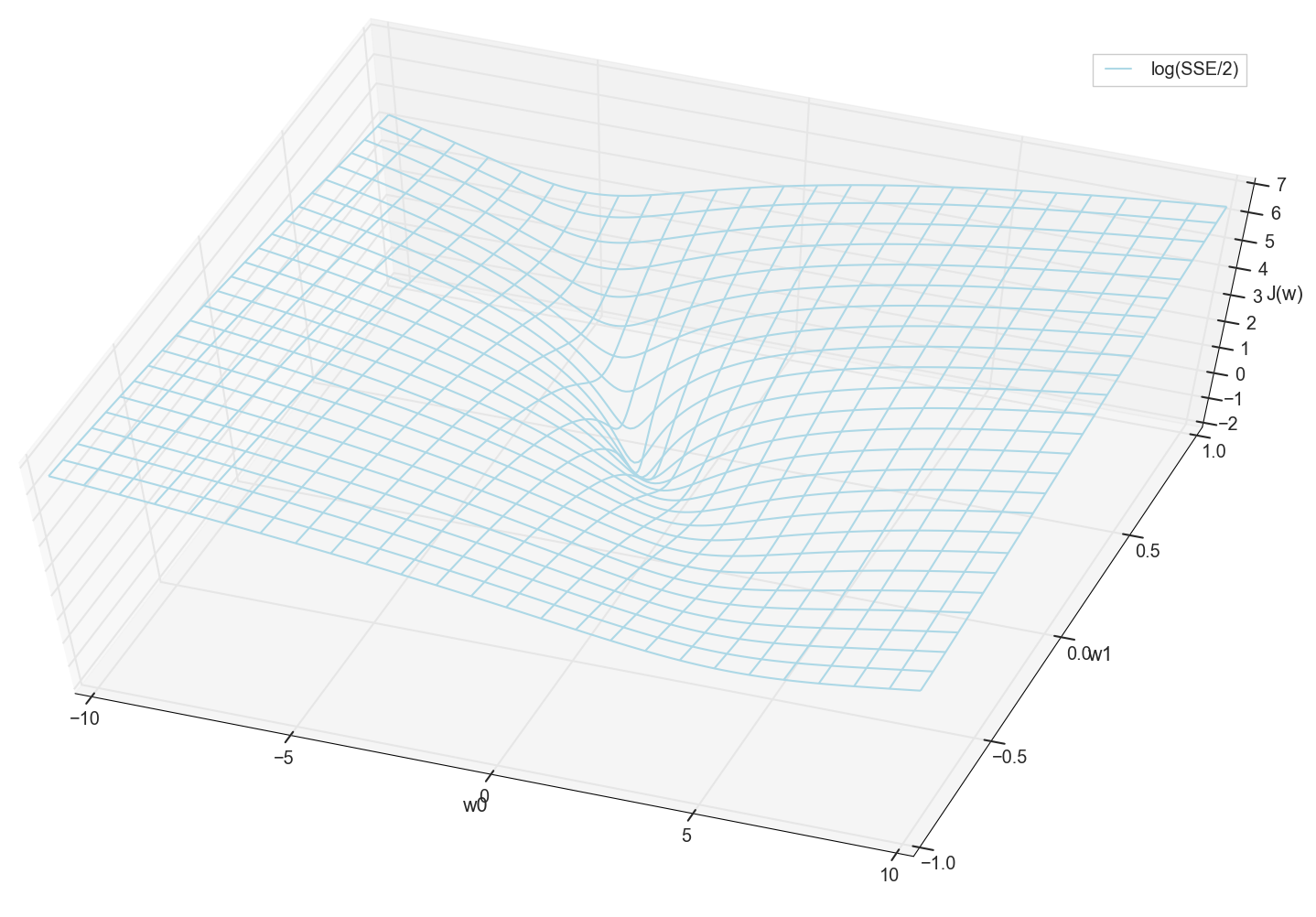
Saya tidak tahu tentang Anda, tetapi secara pribadi, ketika saya melihat bagan ini untuk pertama kalinya, saya mengalami pencerahan. Rongga alami ini bukan hanya visualisasi figuratif dari bukit multidimensi dari artikel populer di jaringan saraf, ini adalah grafik nyata.
Tugas kami adalah memilih nilai-nilai tersebut w0 dan w1 untuk sampai ke dasar lubang ini. Kami mendapatkan nilai bobot - kami mendapatkan neuron yang terlatih.
Karena kita semua sama-sama membuat grafik dan secara pribadi mengamati minimumnya, tidak seorang pun akan melarang kita untuk menemukan koordinatnya dengan enumerasi sederhana di grid "secara manual":

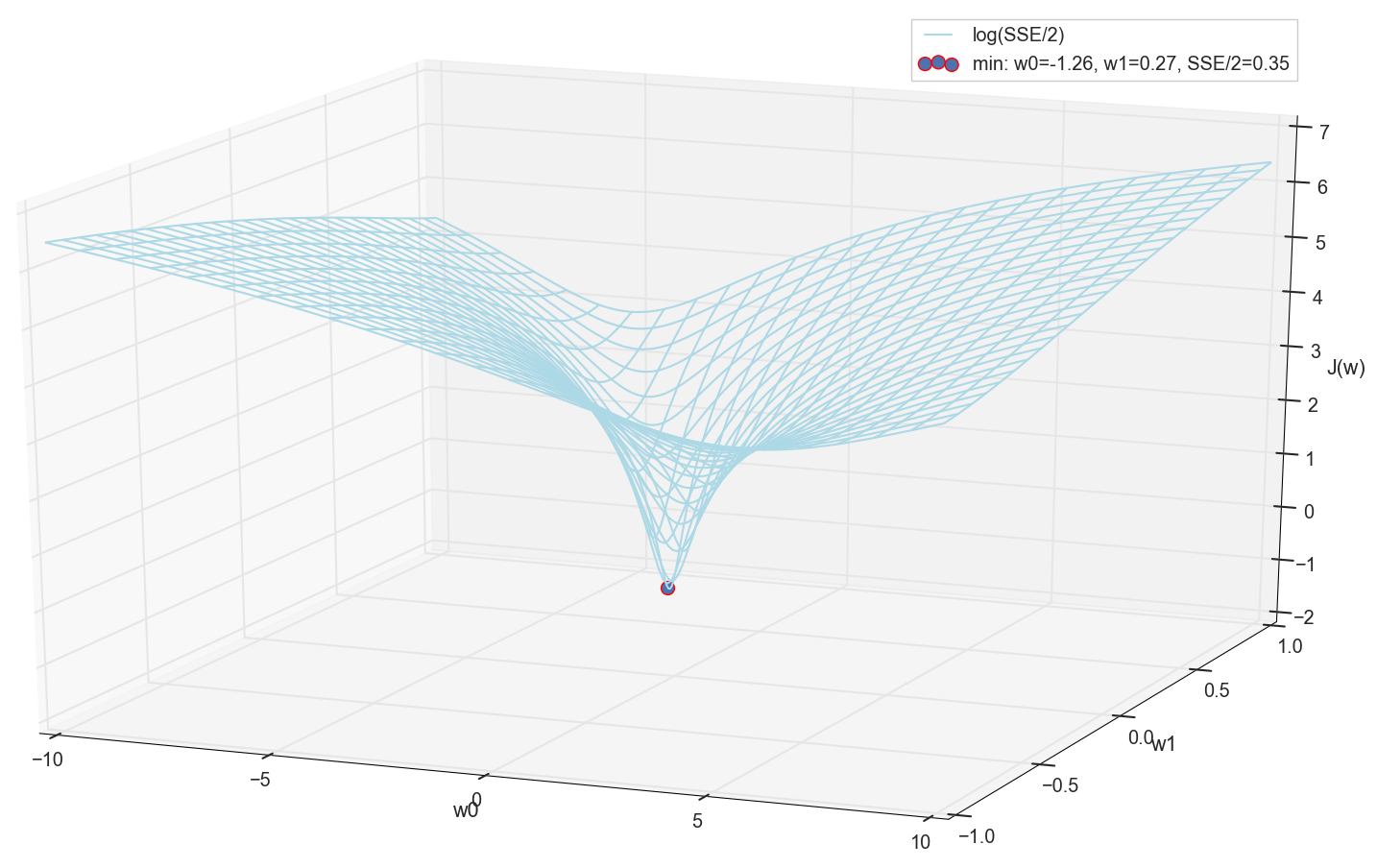
Inilah nilainya: w0=−1,26 dan w1=0,27 , jumlah kesalahan kuadrat dari SSE adalah 0,69, fungsi biaya J(w)=SSE/2=0,35 (lebih tepatnya: 0,3456478371758288).
Mari kita lihat bagaimana aktivasi terlihat dengan parameter ini:

Bagi saya, itu cukup normal. Titik potong aktivasi dengan ambang nol memisahkan elemen dari kelas yang berbeda, dan aktivasi itu sendiri memberi mereka nilai yang benar. Pada saat yang sama, aktivasi tampaknya berada dalam posisi optimal.
Sebelum melanjutkan, kami kembali mengagumi grafik di grid yang lebih luas:
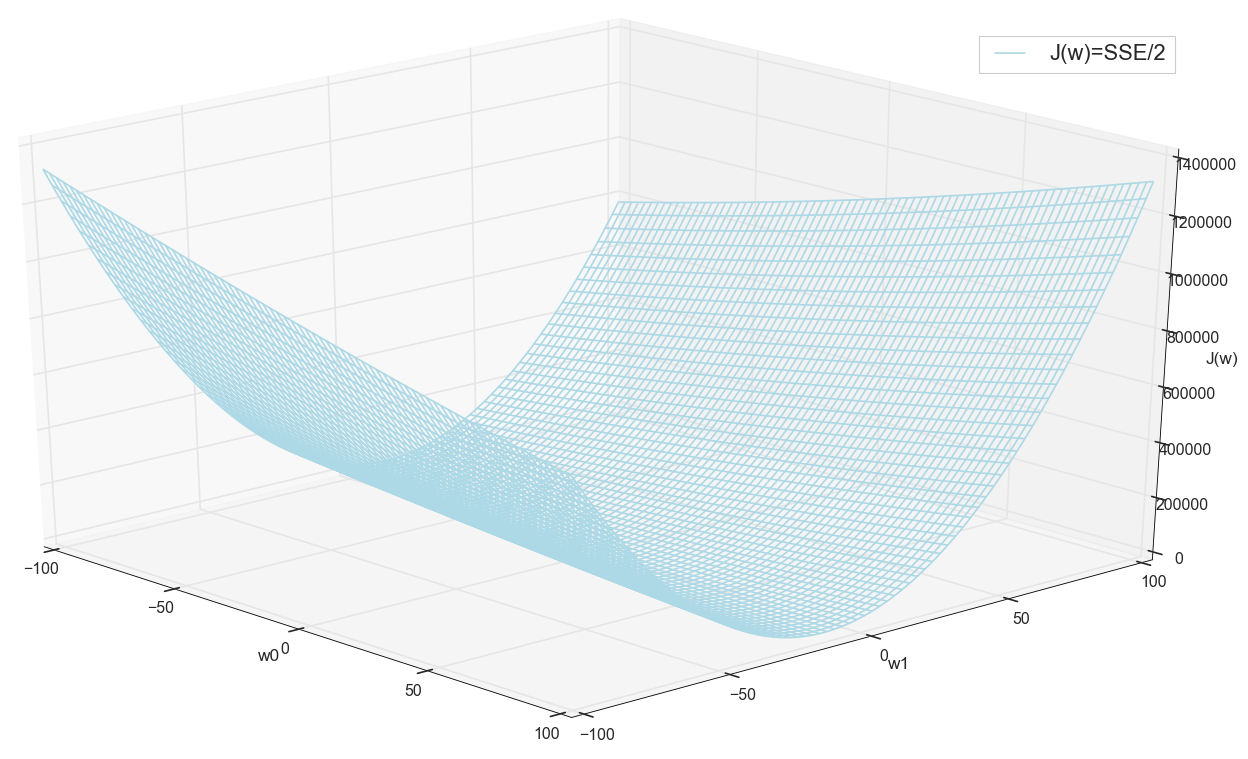
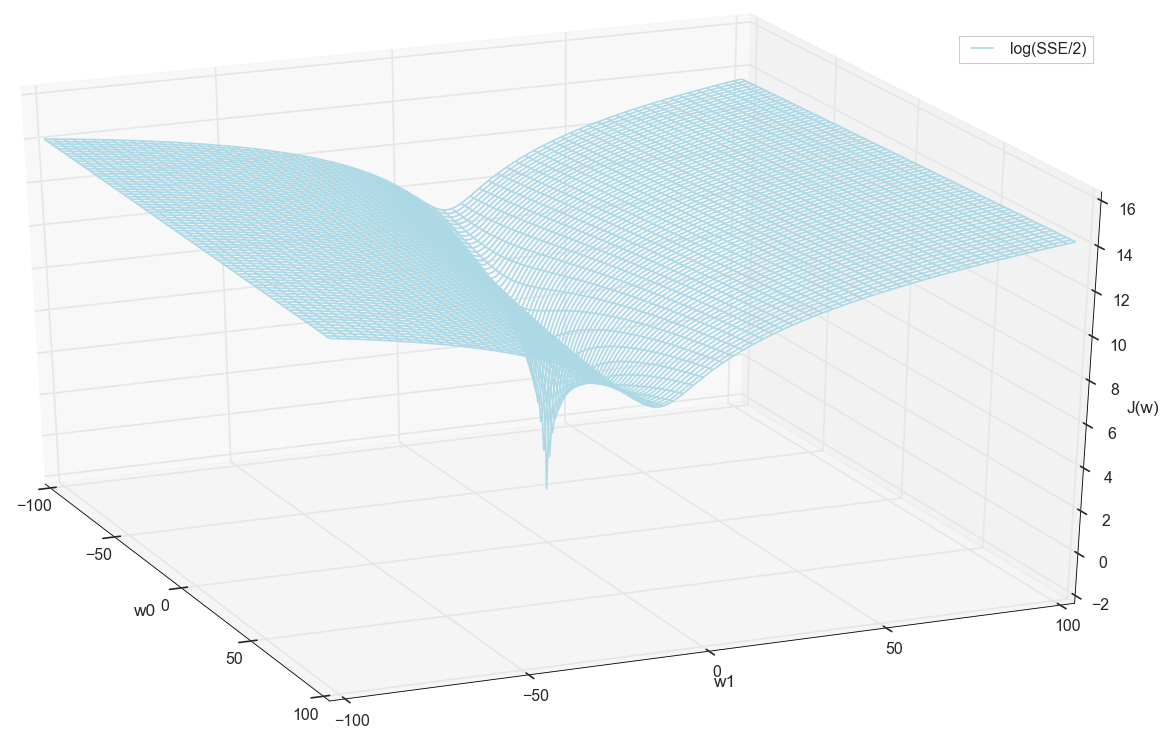
Tampaknya tidak ada posisi terendah lain di dekatnya yang akan berpikir.
Pencarian minimum
Jadi, kami mendapat bobot - koordinat nilai kesalahan minimum. Ini akan menjadi nilai optimal dari bobot pada sampel pelatihan. Secara umum, inilah yang kita butuhkan, kita dapat mengatakan bahwa neuron dilatih. Mungkin ini bisa diselesaikan?
Cari minimum: cari berdasarkan kisi
- Sekilas opsi ini cukup berfungsi (seperti yang kita lihat)
- Anda harus tahu sebelumnya area tempat mencari minimum (Anda dapat mengambil batas yang cukup besar, lalu mempersempit area pencarian - ini hanya dengan mata)
- Untuk meningkatkan akurasi, Anda perlu mengurangi langkah → bahkan lebih banyak poin (solusi: Anda dapat secara sempit mempersempit area pencarian)
- Terlalu banyak poin (untuk 2d mungkin ok, tapi untuk kasus multidimensi kita berlari ke sumber daya dengan sangat cepat)
- Untuk MNIST (28x28 = 784 piksel - jumlah input yang sama, faktor bobot yang sama plus offset, kisi 100 langkah per dimensi): 100 ^ 785 = 10 ^ 1570.
Jadi, jika kita ingin melatih satu neuron (bahkan bukan jaringan saraf) dalam gambar 28x28 = 784 piksel dengan mencari minimum dengan penghitungan langsung pada kisi 100 titik untuk setiap pengukuran, kita perlu memilah 10 ^ 1570 kombinasi. Ini cukup banyak untuk penyimpanan dan pencarian (di bagian Semesta yang terlihat hanya ada 10 ^ 80 atom, Semesta ada selama sekitar 4 * 10 ^ 17 detik = 4 * 10 ^ 26 nanodetik).
Mari kita coba mencari opsi lebih cepat.
Pencarian Minimum: Keturunan Langkah Konstan
Mari kita lihat grafik dari fungsi kerugian J(w) di pesawat: perbaiki w0 berubah w1
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
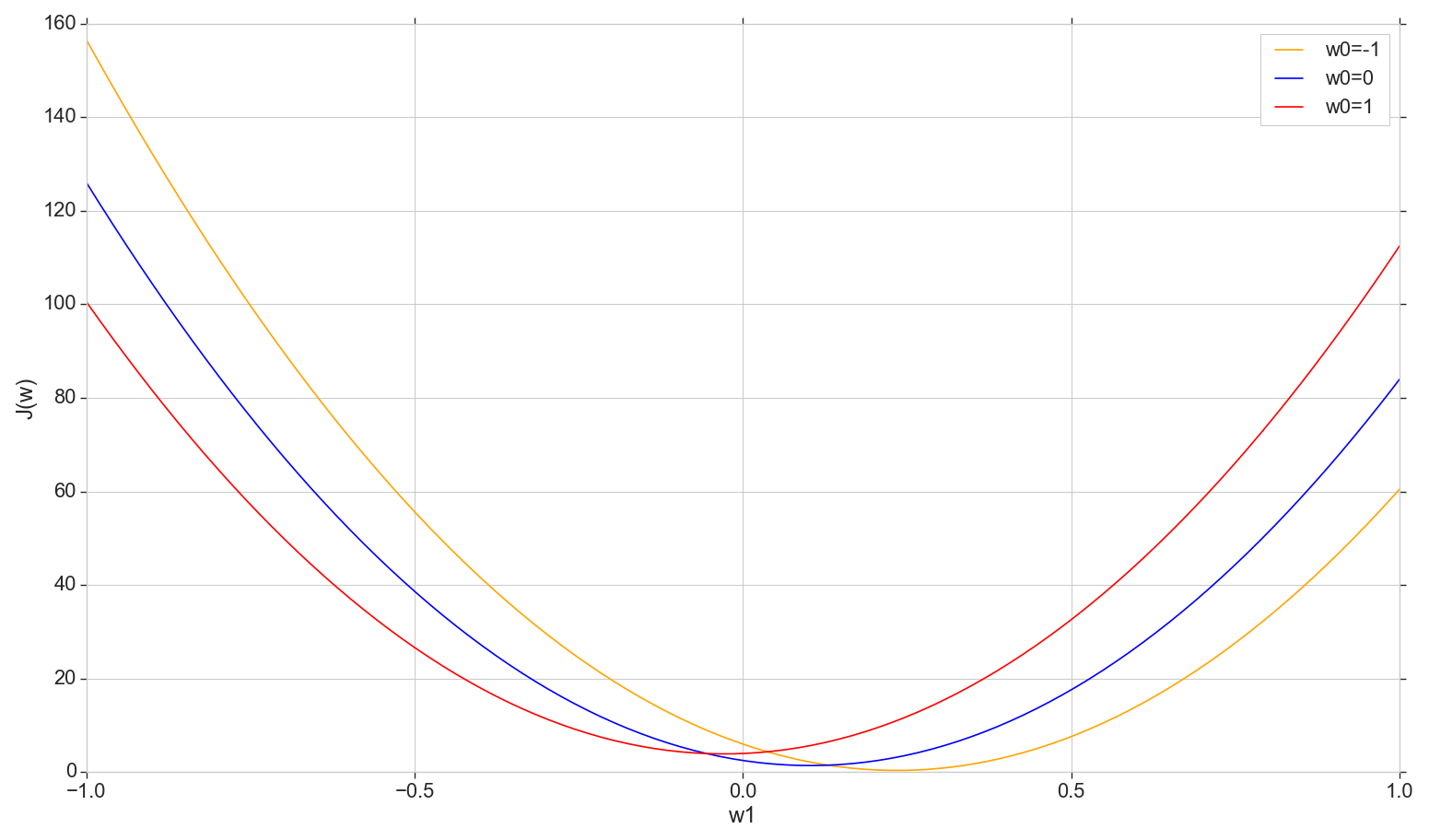
Ini adalah parabola biasa (lebih tepatnya, keluarga parabola - mereka akan sedikit berbeda tergantung pada apa nilai yang ditetapkan pada w0 ) Untuk menemukan parabola minimum, tidak perlu memilah-milah semua poin. Kita dapat memilih titik sembarang pada sumbu horizontal dan bergerak menuju minimum dengan beberapa langkah.
Pertimbangkan opsi nada yang konstan
- Jika langkah terlalu besar, Anda dapat meleset, dan tidak mencapai minimum (langkah tersebut dapat dikurangi)
- Jika terlalu kecil, akan ada terlalu banyak langkah (lebih dari yang seharusnya)
- Bagaimanapun, kami tidak akan mencapai minimum yang tepat, tetapi kami dapat mencapainya dengan akurasi sewenang-wenang dengan mengubah langkah di dekat minimum yang tidak akurat yang ditemukan (langkah tidak lagi konstan)
- Kami tidak tahu arah penurunan (dimungkinkan untuk menyelesaikan secara algoritmik: jangan melangkah ke arah meningkatnya kesalahan)
- Masalah dengan menemukan rentang telah diselesaikan (Anda dapat turun dari mana saja - cepat atau lambat kami akan turun pula)
- Pada prinsipnya, opsi ini berfungsi, tetapi mungkin ada opsi yang lebih baik?
Catatan: ketika saya berbicara tentang opsi turun ke kuliah, seorang siswa bertanya mengapa Anda perlu bergerak dalam langkah-langkah jika Anda dapat segera menemukan parabola minimum menggunakan rumus? Pada awalnya, saya menjawab sesuatu dengan semangat sehingga kami sekarang tertarik untuk mempertimbangkan opsi iterasi, sehingga nantinya kami dapat menggunakannya tidak hanya dengan parabola, tetapi juga dalam situasi lain. Plus, pada kenyataannya, kami tidak membutuhkan setidaknya parabola khusus pada bagian ini - kami akan pindah ke minimum tidak dalam satu dimensi, tetapi dalam semua dimensi sedemikian rupa sehingga pada setiap iterasi baru langkah baru akan berlangsung tidak sepanjang parabola ini, tetapi pada parabola dengan irisan baru dengan nilai bergeser w0 . Tetapi berpikir kemudian, saya berpikir bahwa, pada prinsipnya, tidak ada yang salah jika kita bergerak di setiap irisan, tidak dalam langkah-langkah, tetapi segera turun ke minimum irisan saat ini. Jadi, dari waktu ke waktu, pengukuran demi pengukuran, kita masih harus meluncur ke minimum global, dan tampaknya lebih cepat daripada langkah-langkahnya. Untuk satu neuron, ia seharusnya bekerja, dan tidak hanya dengan parabola. Tetapi saya belum mulai membuang waktu untuk menguji teori ini, jadi di sini kita lanjutkan saja - saya berjanji untuk berbicara tentang gradient descent.
Cari minimum: gradient descent
Secara umum, kami menuruni tangga, tetapi kami melakukannya dengan lebih cerdas. Kami menggunakan turunan dari kurva biaya untuk memilih langkah (di sini, bukan kurva biaya , tetapi kurva biaya ).
- Kami memiliki beberapa dimensi dan masing-masing memiliki kurva sendiri: kami memperbaiki semuanya wj kecuali wk ,
- J(wk) akan ada kurva kesalahan di k dimensi th
- Semuanya adalah (dalam kasus kami) parabola, tetapi, secara umum, hanya penting bahwa mereka dapat dibedakan di mana-mana dan memiliki minimum
- Untuk menyesuaikan langkah dalam setiap pengukuran, kami akan menggunakan turunan parsial dari fungsi kesalahan sehubungan dengan pengukuran ini (koefisien yang bervariasi wk )
- Vektor dari turunan parsial seperti itu disebut gradien.
Ini semua baik, tetapi dari mana turunannya berasal? Sekarang mari kita cari tahu.
Arti geometris dari turunan
Bagi saya, turunan untuk waktu yang lama tetap satu set formula dan aturan khusus untuk perhitungannya, ditambah sesuatu tentang kenaikan, penurunan, dan ekstrem. Di sini akan tepat untuk mengingat atau mencari tahu apa sebenarnya derivatif itu.
Fungsi turunan y(x) pada titik ini x0 Apakah batas rasio kenaikan fungsi Deltay untuk kenaikan argumen Deltax saat menambah argumen Deltax cenderung nol:
y′(x0)= lim Deltax to0 Deltay over Deltax, Deltay=y(x0+ Deltax)−y(x0)

Titik di gambar M(x0,y(x0))=(x0,y0) Adalah titik di mana kita ingin menentukan turunannya. Point N(x0+ Deltax,y(x0+ Deltax))=(x0+ Deltax,y0+ Deltay) - Poin yang diperoleh dengan menambah argumen Deltax . Langsung Mn - Garis potong melewati dua titik ini.
Point A - persimpangan garis potong Mn dengan sumbu horizontal y=0 .
Pertimbangkan dua segitiga siku-siku: segitiga segitigaNPM dengan bagian garis potong Mn sebagai sisi miring dan segitiga segitigaMBA dengan kelanjutan garis potong pada sumbu y=0 - segmen AM sebagai sisi miring. Dari grafik dan geometri sekolah tentu terlihat jelas sudutnya angleNMP dan angleMAB sama, dan oleh karena itu garis singgung mereka sama:
tan angleMAB= tan angleNMP=MB overAB=NP overMP= Deltay over Deltax
Tambahkan ke gambar: MD - bersinggungan dengan kurva awal pada titik tersebut M melintasi sumbu y=0 pada intinya D . Segitiga triangleMBD - segitiga siku-siku dengan sisi miring - bagian kaset, ruas MD .
Kami mengincar kenaikan tersebut Deltax ke nol:
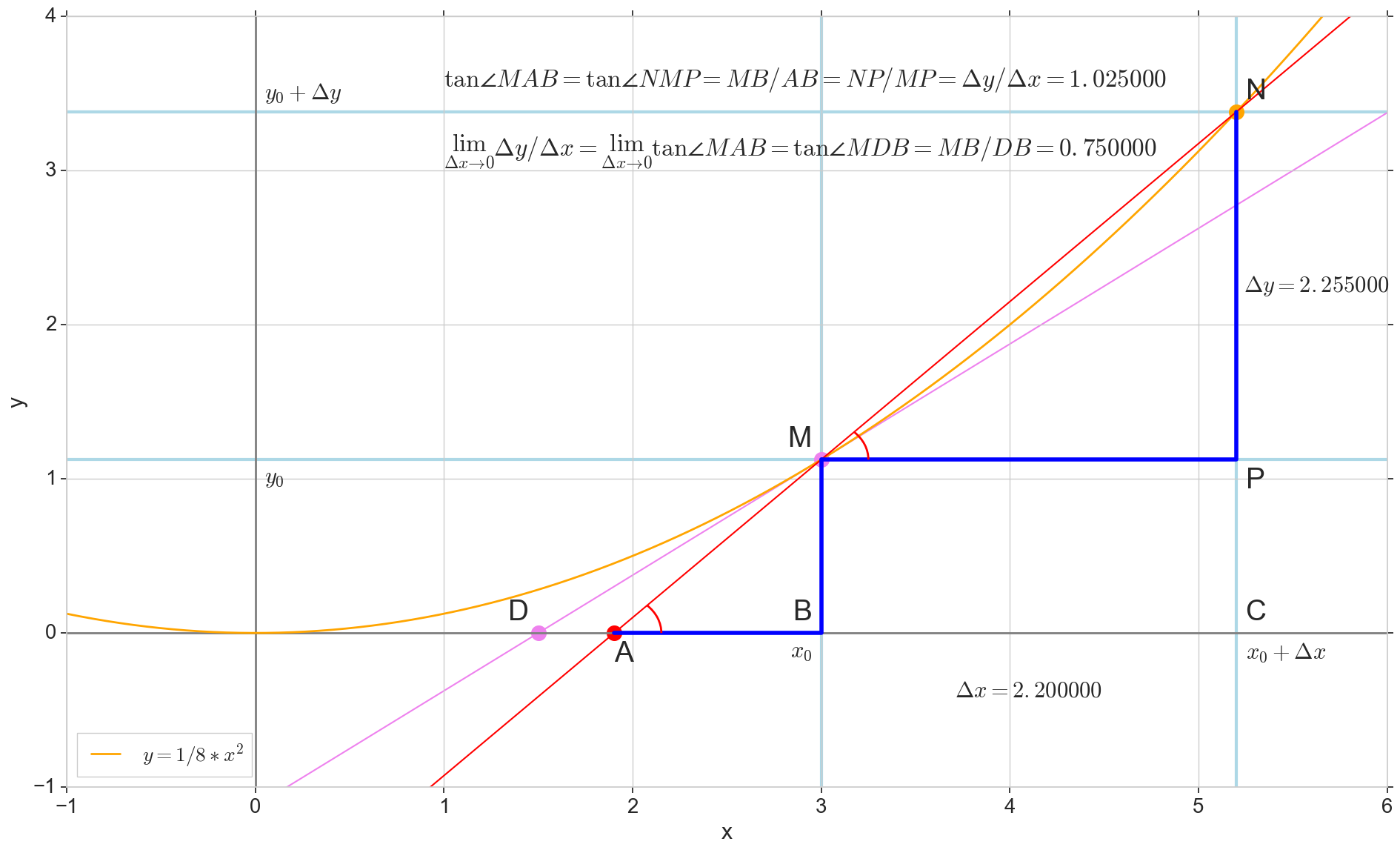
Point N pindah ke titik M berdasarkan fungsi, titik A merayap ke suatu titik D sepanjang sumbu y garis potong Mn berubah menjadi garis singgung MD dengan titik sentuh M . Sumber segitiga segitigaNPM dengan kaki Deltax dan Deltay menyusut ke suatu titik, tetapi segitiga seperti itu segitigaMBA berubah menjadi segitiga triangleMBD melestarikan tidak hanya dimensi makroskopis, tetapi juga persamaan sudut angleMAB dan angleNMP .
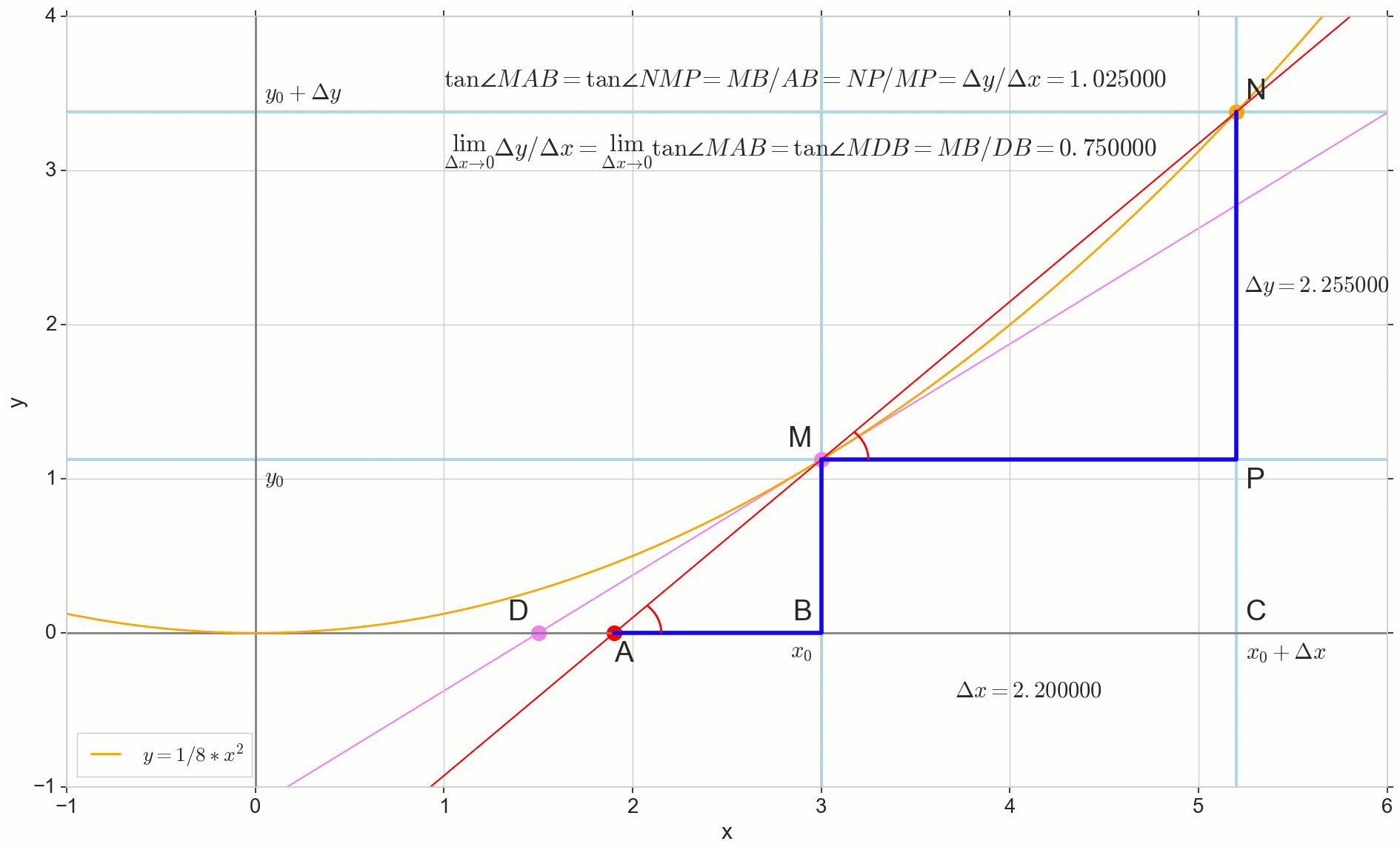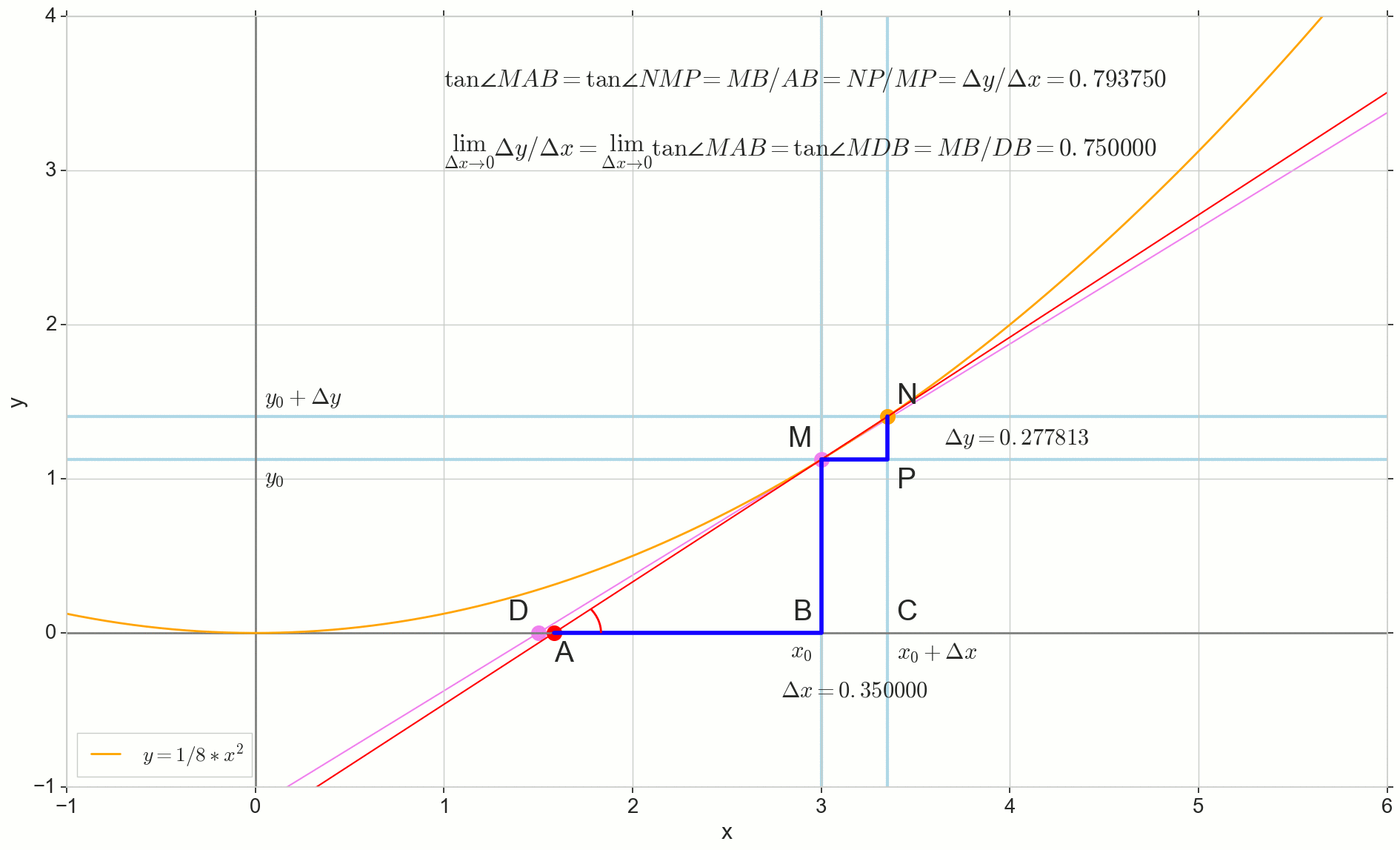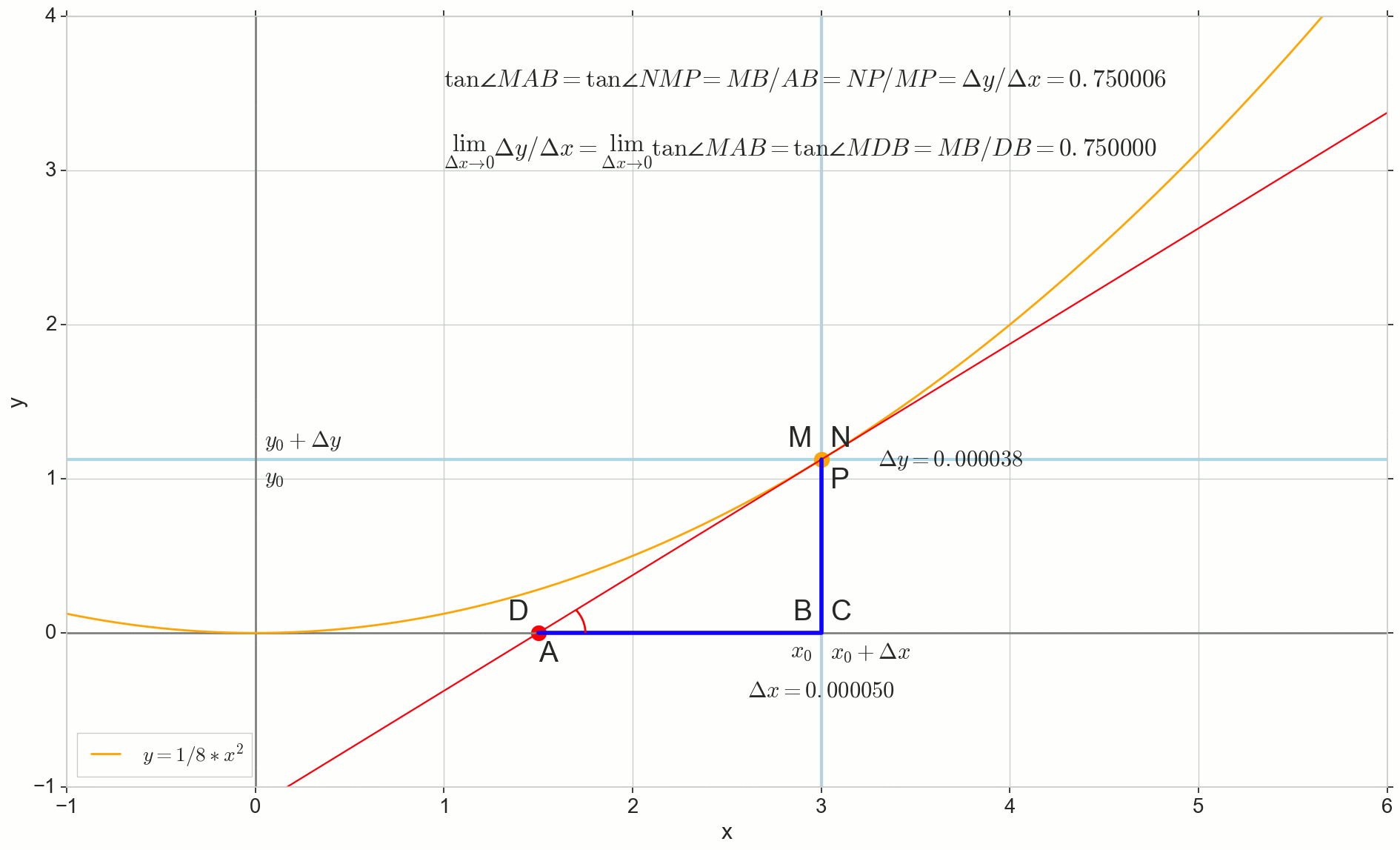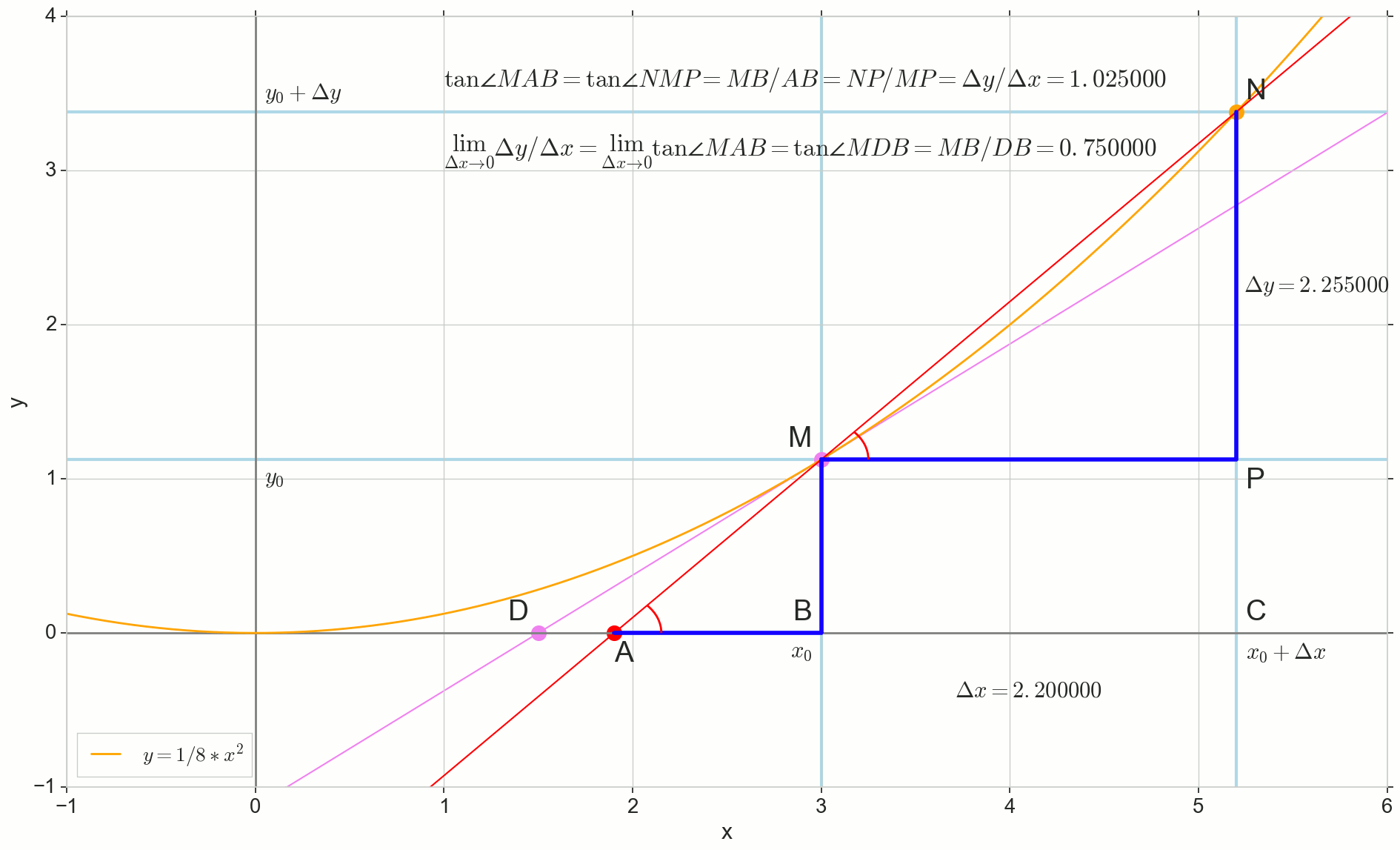
Bagaimana kenaikannya Deltax , mendekati nol tanpa batas, tidak akan pernah mencapai nol, begitu intinya N tidak pernah sampai ke tempat yang tepat M titik A tidak akan mencapai titik D segitiga segitigaMBA tidak akan berubah menjadi triangleMBD . , , «» lim .
△MBA — △MBD , :
limΔx→0ΔyΔx=limΔx→0tan∠NMP=limΔx→0tan∠MAB=limΔx→0MBAB=MBDB=tan∠MDB
:
limΔx→0ΔyΔx=tan∠MDB
, , :
y′(x0)=limΔx→0ΔyΔx=tan∠MDB
, y=0 . .
, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).
:
- x0 y=0
- — y(x0) — x0 y=0 y=0
- «» , ,
- — : — , —
- ( , , , Δy )
, , :

— , — x0 , — . — — . — y=0 , — .

, , , , . ( , ) (: y=0 , ).

( ): , (: y=0 , ).
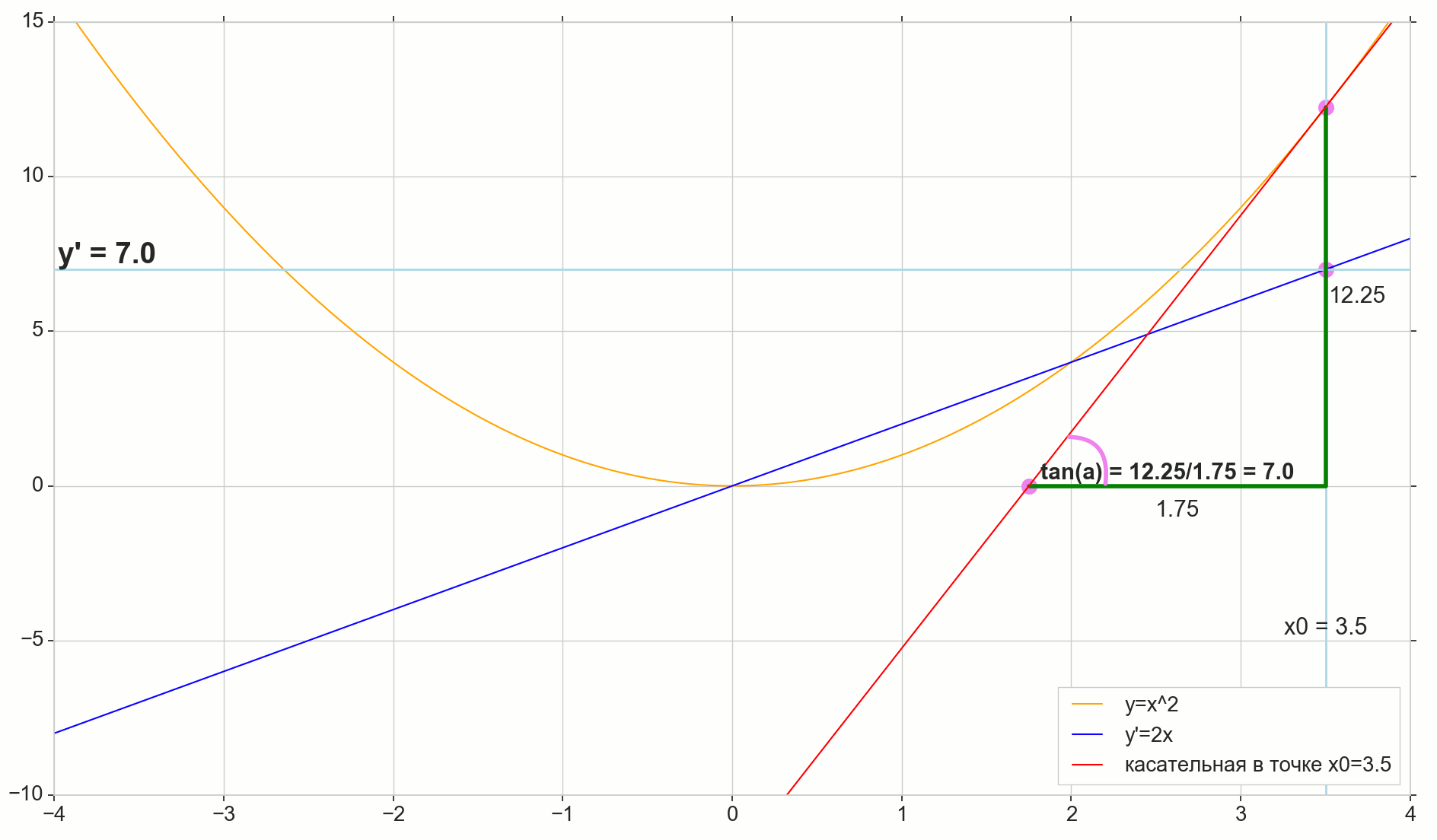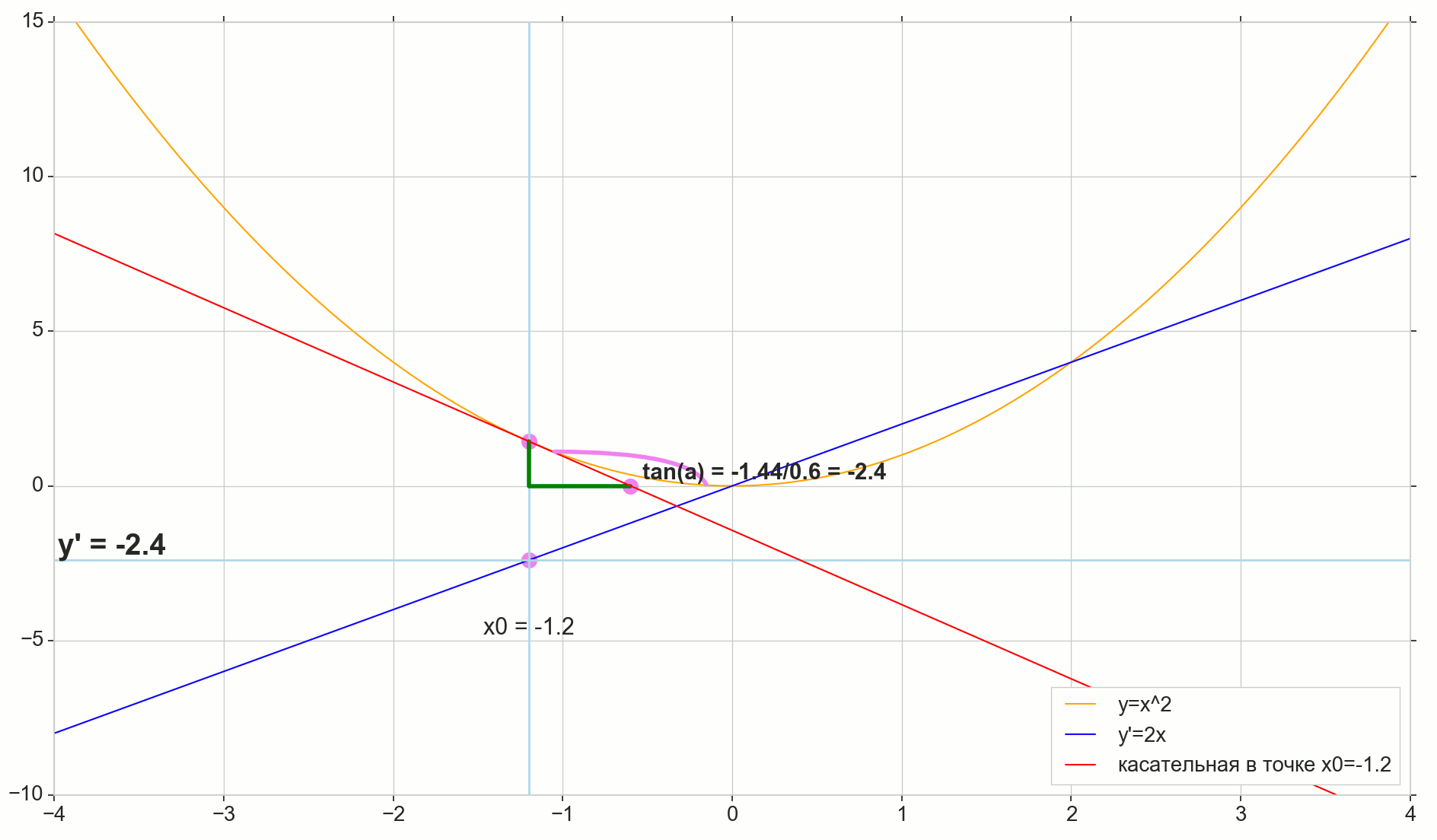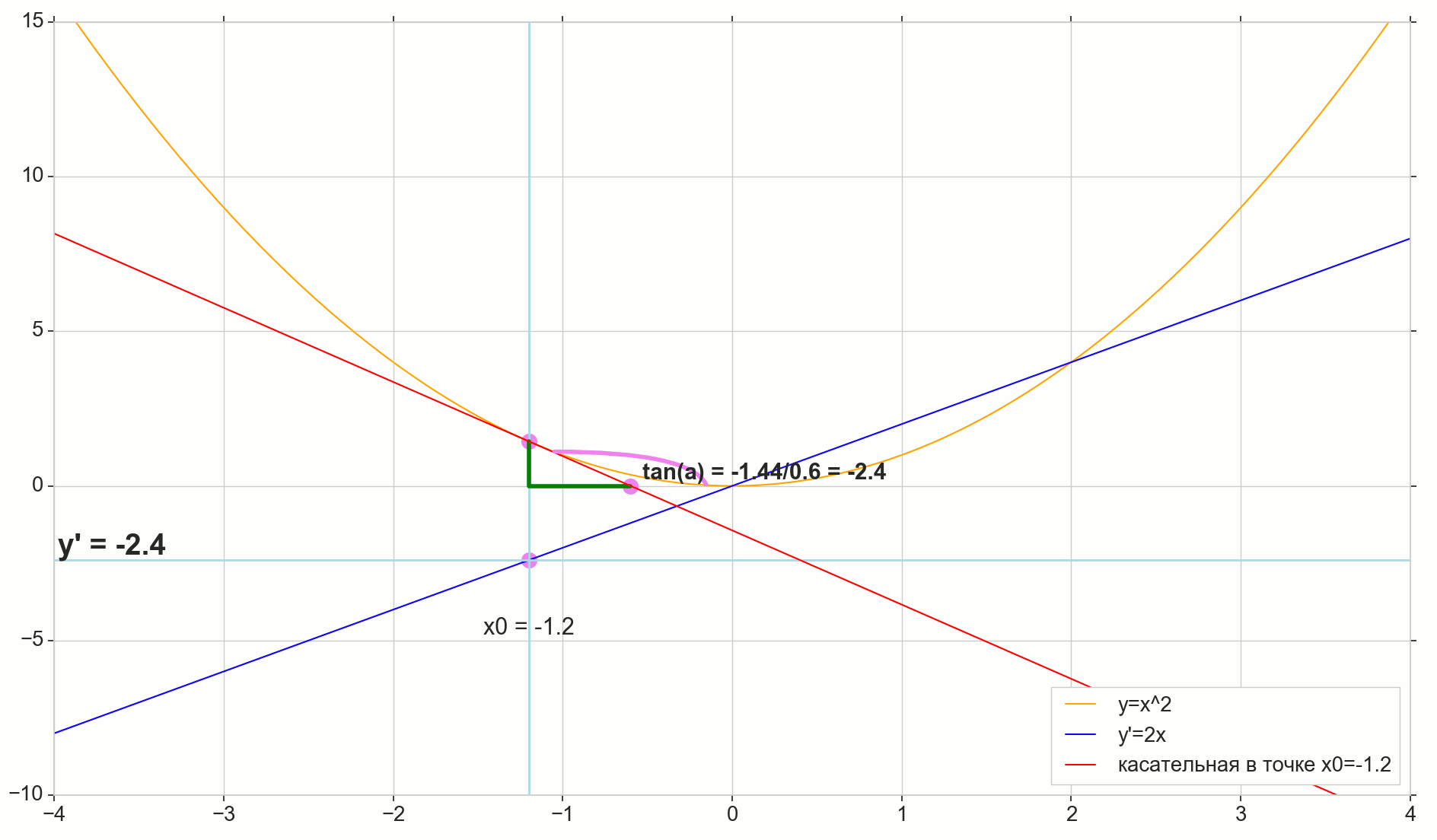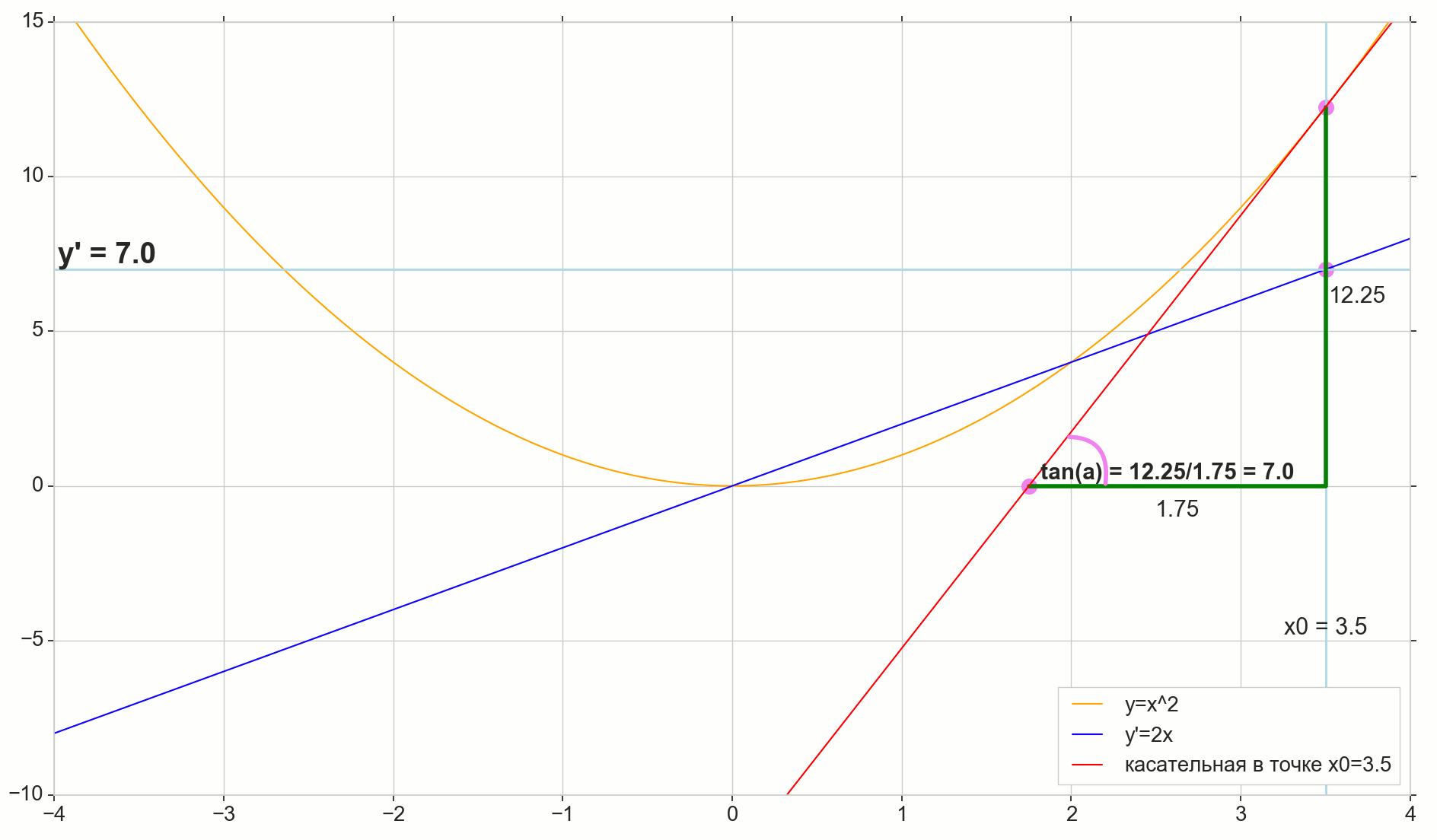
, : (), «»/«» , . — . , , ? .
J(w) . , , , .
J(w)=12SSE=12n∑i=1(m∑j=0wjx(i)j−y(i))2
∂J(w)∂wk=∂∂wk12n∑i=1(m∑j=0wjx(i)j−y(i))2=12n∑i=1∂∂wk(m∑j=0wjx(i)j−y(i))2=12n∑i=12(m∑j=0wjx(i)j−y(i))∂∂wk(m∑j=0wjx(i)j−y(i))=122n∑i=1(m∑j=0wjx(i)j−y(i))∂∂wk((w0x(i)0+...+wkx(i)k+...+wmx(i)m)−y(i))=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
, : , , , ( ) . , wk ( , ), . , , , 1/2 SSE .
:
∂J(w)∂wk=n∑i=1(m∑j=0wjx(i)j−y(i))x(i)k
— ( ∇ [], , .. []):
∇J(w)=(∂J(w)∂w0,...,∂J(w)∂wm),w=(w0,...,wm)
:
w:=w+Δw,Δw=−η∇J(w)
k - :
wk:=wk+Δwk,Δwk=−η∂J(w)∂wk
:
, , , . , .
1- :
Φ(x,w)=w0+w1x1
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1−y(i))x(i)0=n∑i=1(w0+w1x(i)1−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1−y(i))x(i)1
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1−y(i))x(i)1
, . .
( w1 )
w0=1 , J(w1)
X ( ) y w0 dan w1 ( ):
def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum()
w1 -1.5 1.5.
, ( , , ):
plt.subplot(3,1,1)

, , δJ(w)δw1 — :
grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left')

Δw1(w1) (, Δw1 w1 , .. , ):
eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right')

plt.show()

- : ,
- : — «» ( , «» ),
- : — ( ), η [] ( ),
: , 1000 .
, ,
w — - - . w0=1 , w1=0.9 . η=0.001 ( , ) 12:
:
w1 J(w1,w0=1) :
Δw1(w1)
plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u' , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange')

, , ( ), . , , , .
: , , , «» , — , .
- — w1 , —
- , w1
- — : , —
- , —
- , ( ), , ( ) — , —
- ( , — ).
- : — , —
- ? — . .
- . w1 , . , «»/«» . , , . , , , « ». , : w1=0.9 200, , , , 1. , , , . — η . , 200 1. η=0.001 , w1=0.9 200*0.001=0.2 ( -1, -0.2) — .
- J(w1=0.9)=92.43 , 12 (, ) J(w1=0.03)=8.54
- , ,
, . , . , ( , ). η , .
: , , , .
, , , .
η
- η [] — ()
- ,
- «»: , , ,
- , J(w)
- : wk , η , wk
η=0.01

. , . 3- , 3- , , .. , .. . , , [] .
η J(w) η

: , , . , — , , .
:

:

.
η . , , .

, .
:
, ( ) w , , . , , , . , , .
,
, .
, :

— :
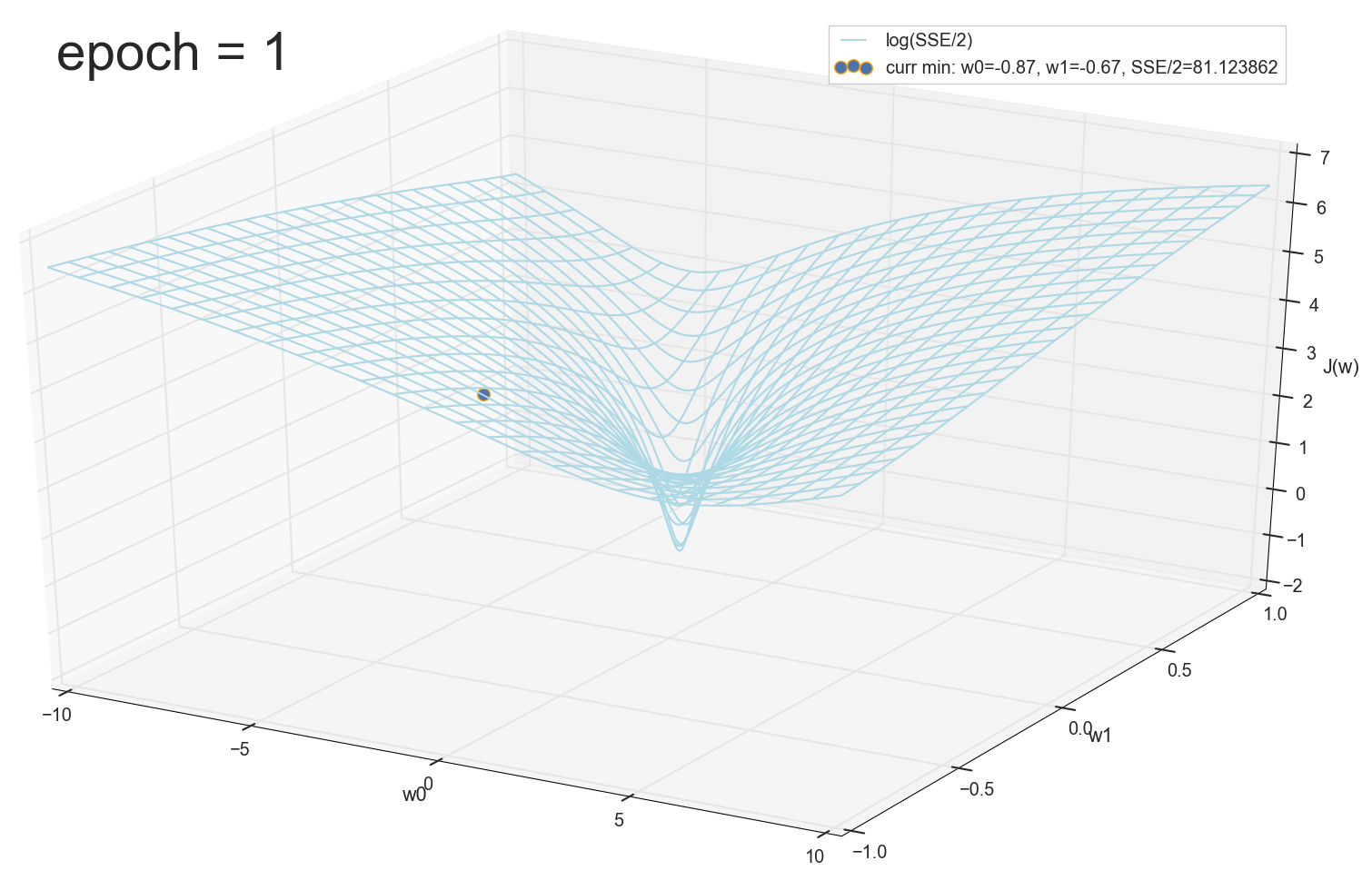
12 — , :

50 :

1767 — , :

, 62000 :

:
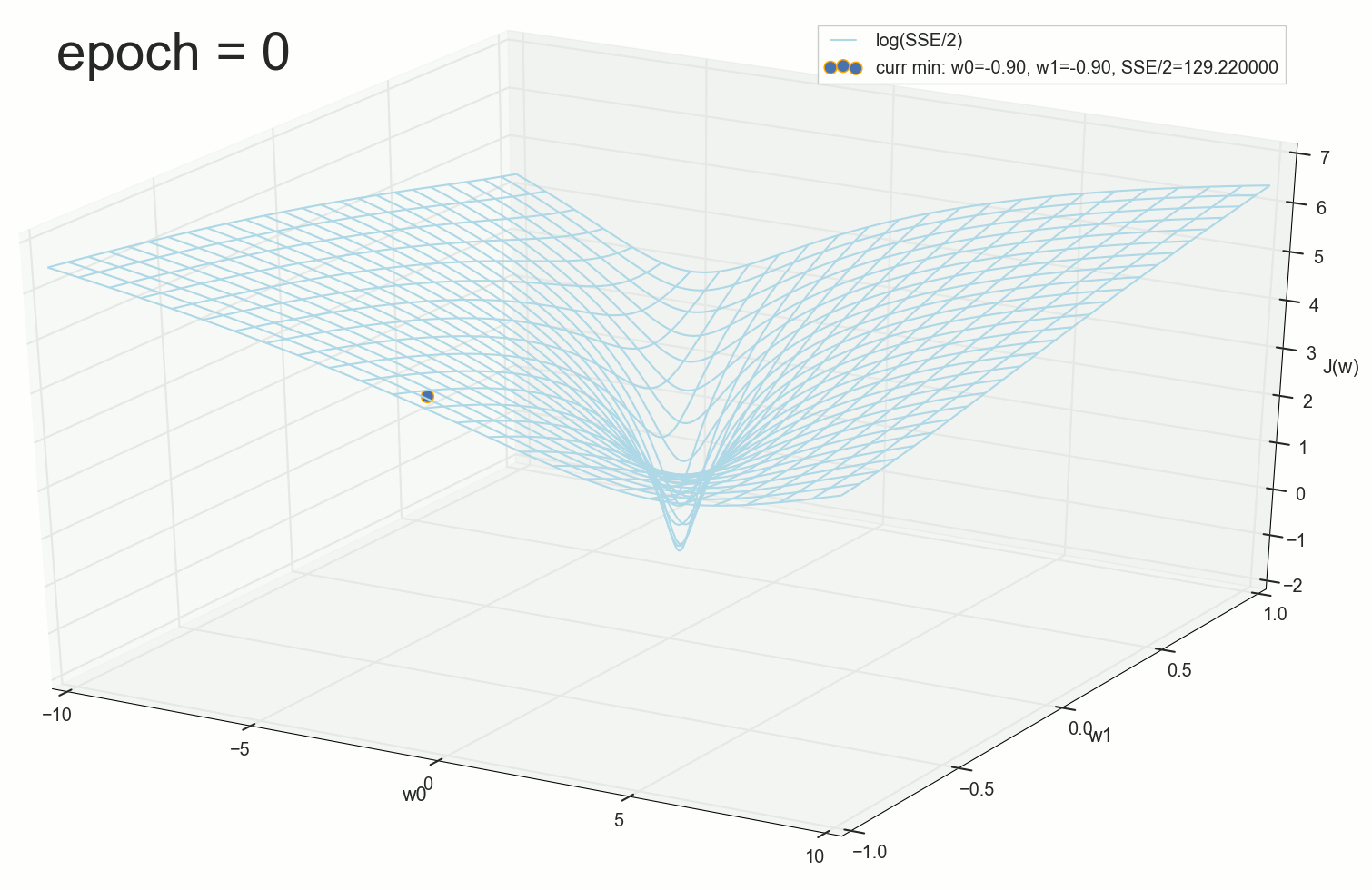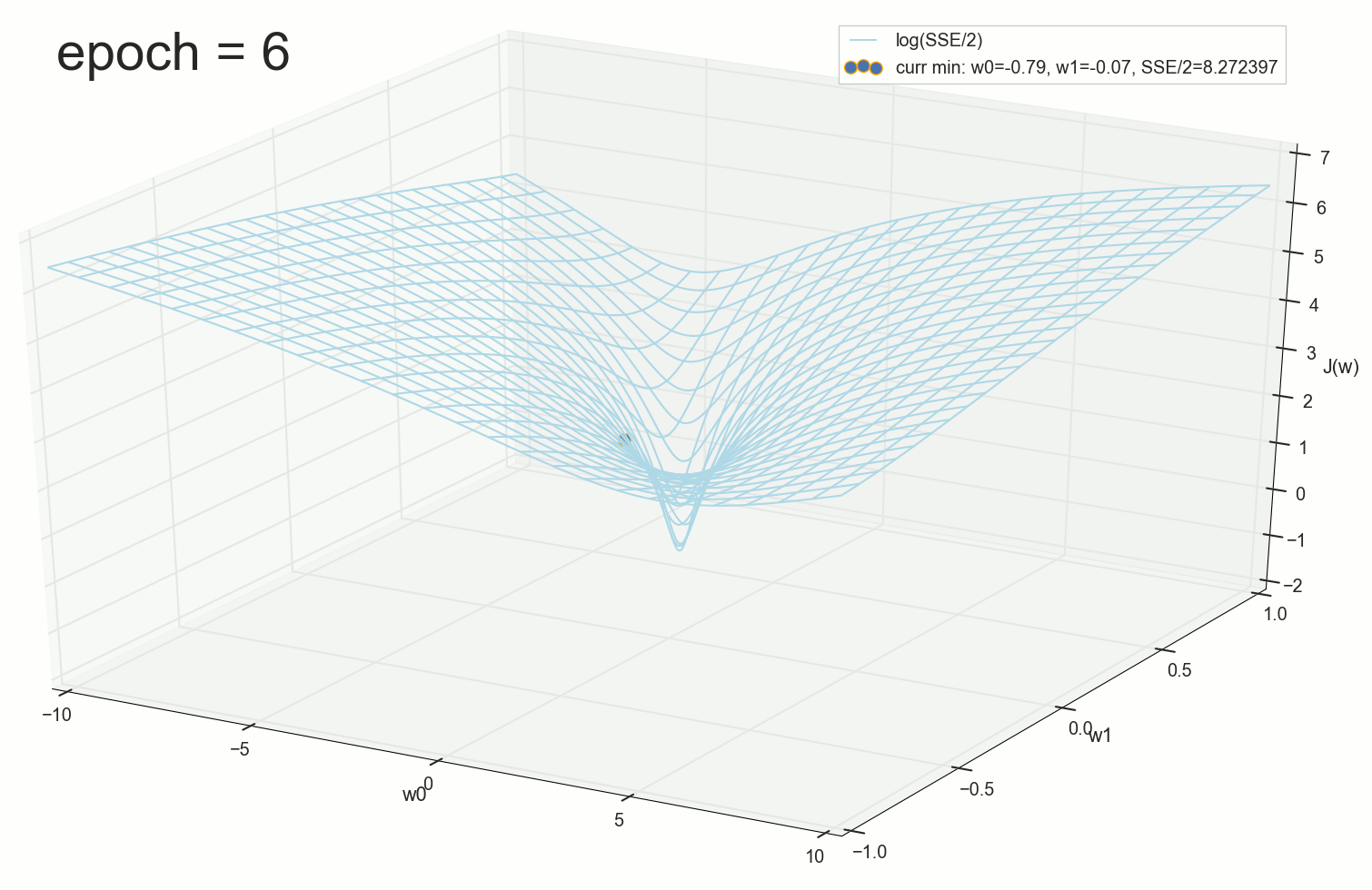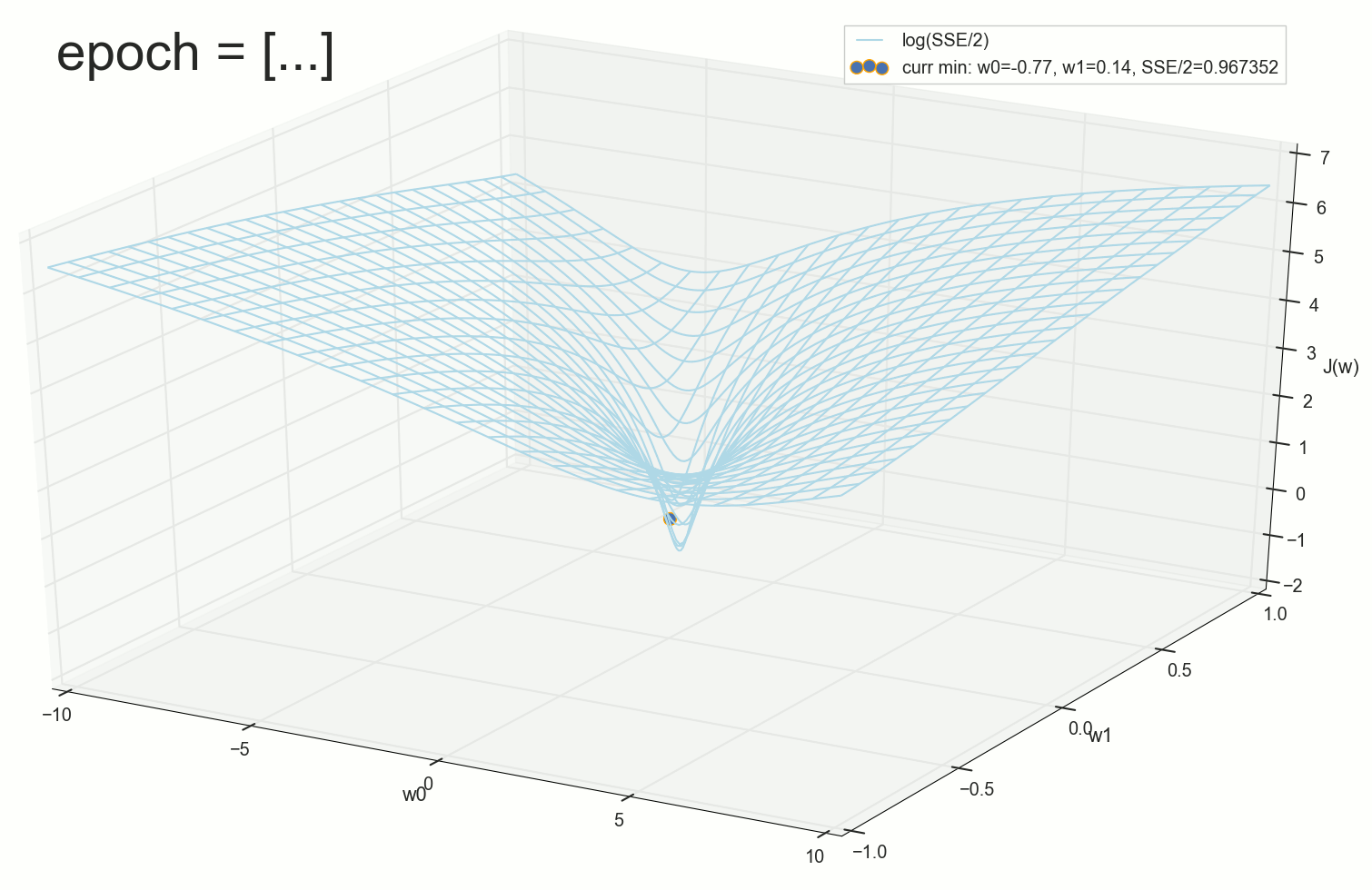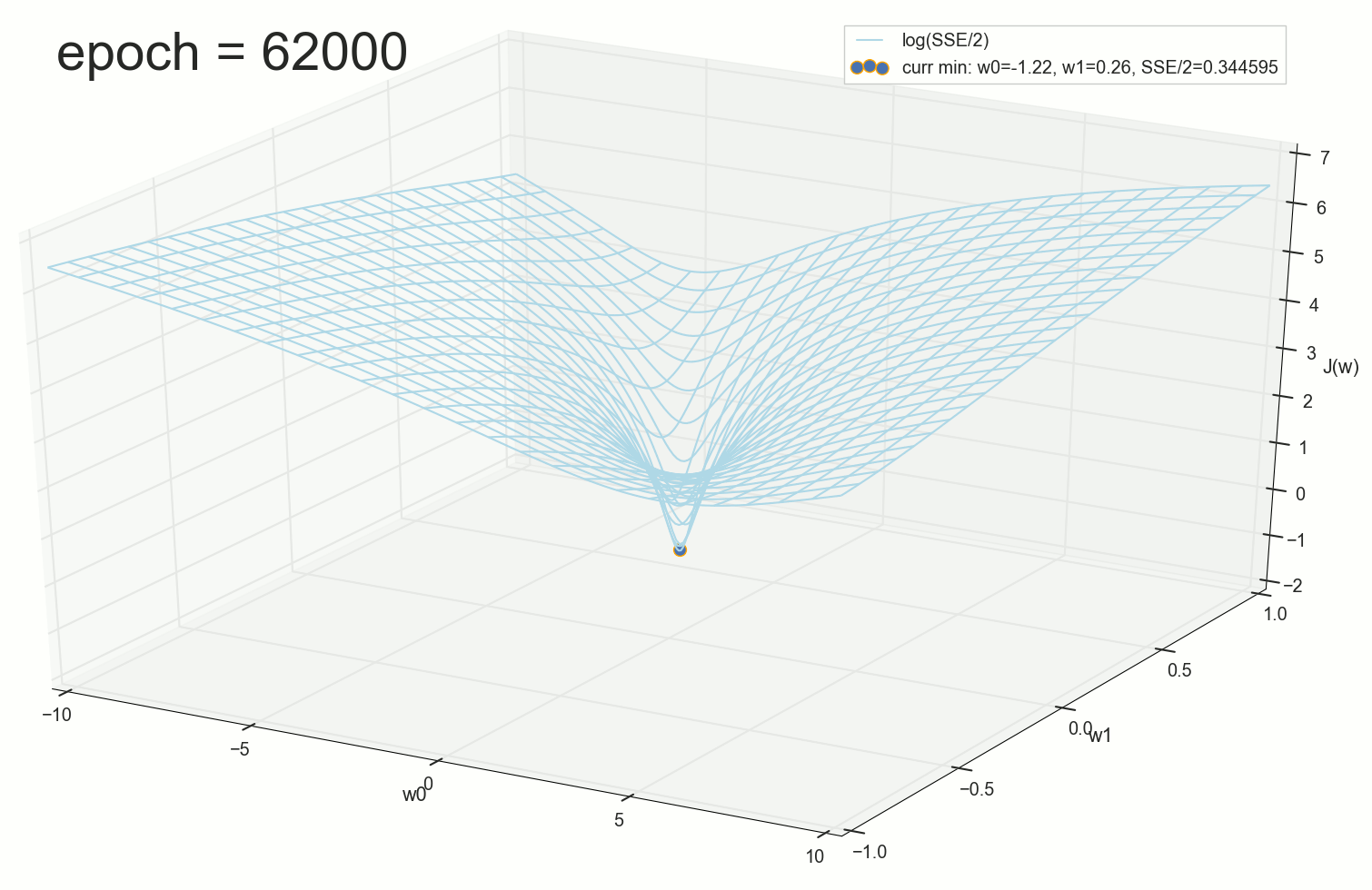
. , : , , . , , , , , , . , , - .
, , - , - : , , , , , — . , , , , , , , — . ?
, . :
, , ( ). : , . , , .
. , .
. , , . , — .

— :

11- : , ; :

12- : , , :

50- : , 12-

1766: . J(w)=0.3456480221 — , , ( J(w)=0.3456478372 : 6- , , )

1767: J(w)=0.34564503 — , ( 6- , ). w0=−1.184831 , w1=0.258455 ( w0 2- : w0=−1.27 , w1=0.26 )

62000: J(w)=0.3445945 — , ( 2- ). :

:
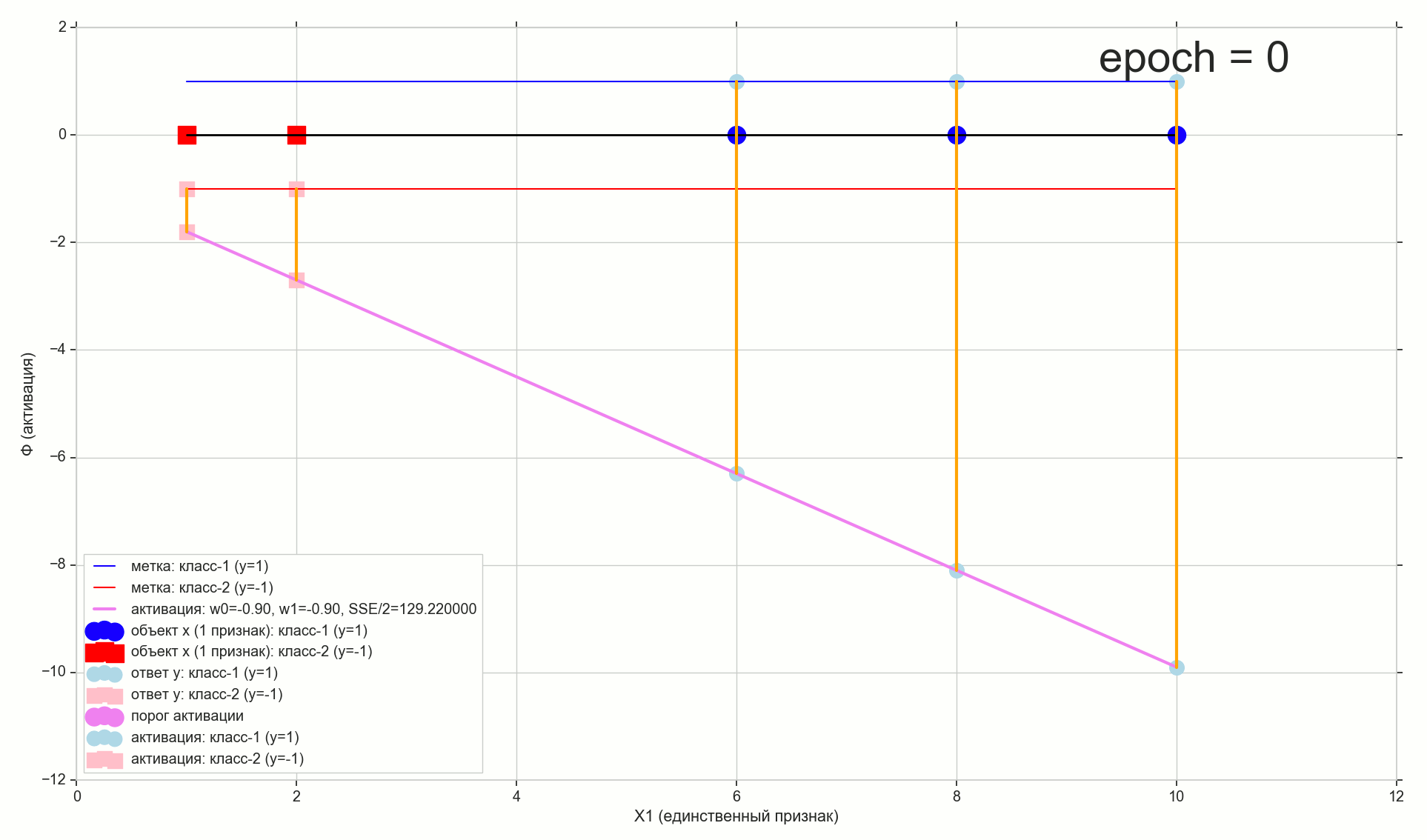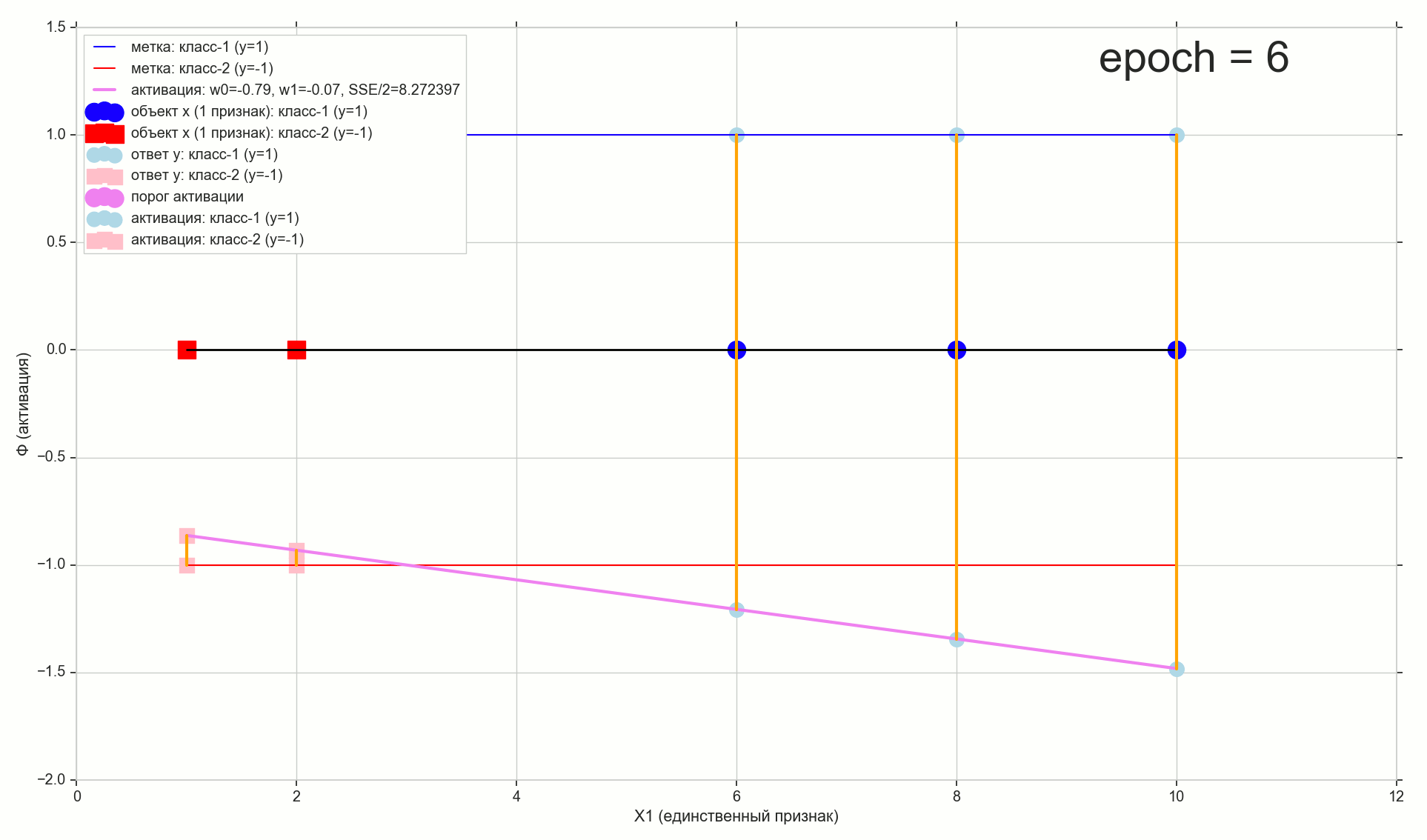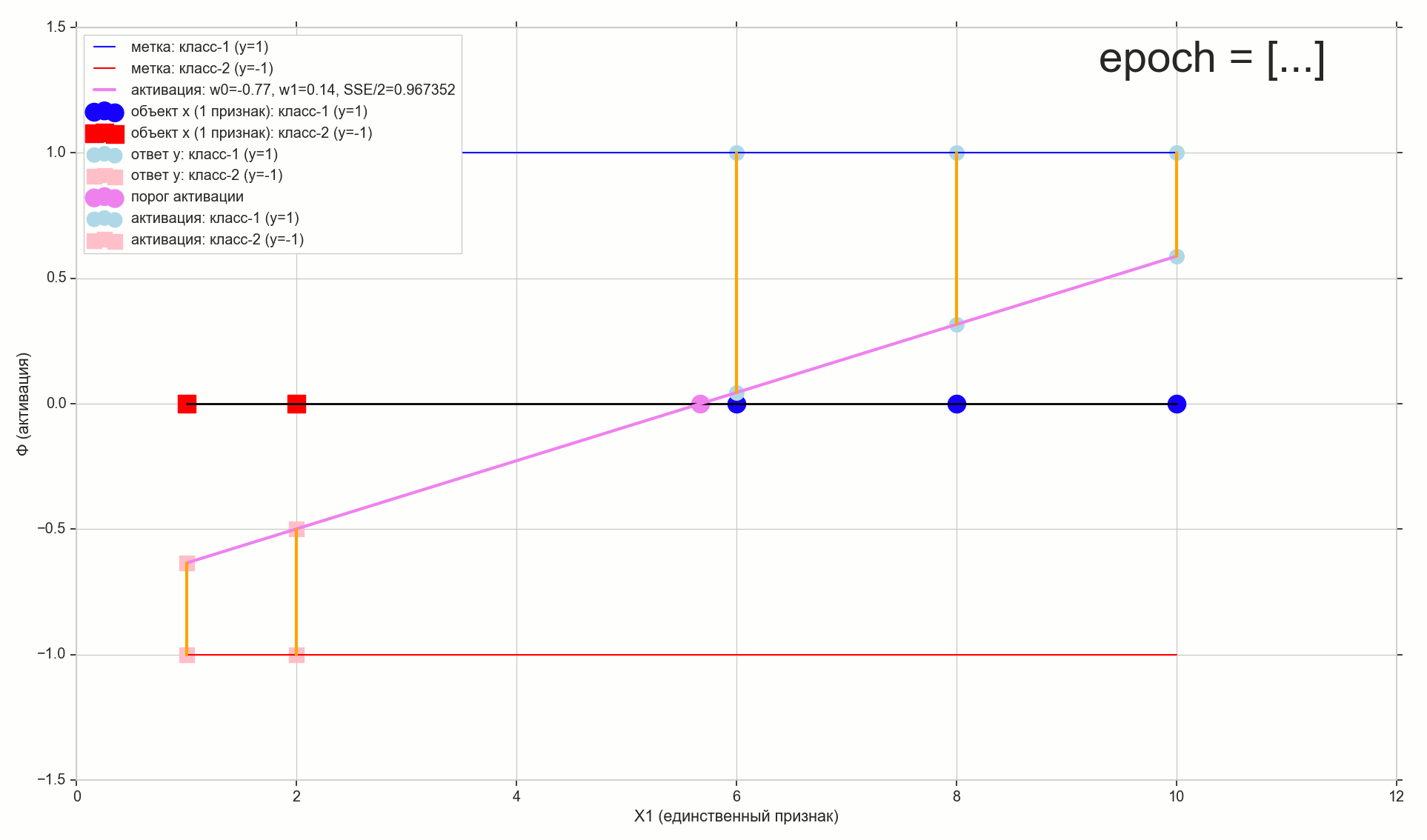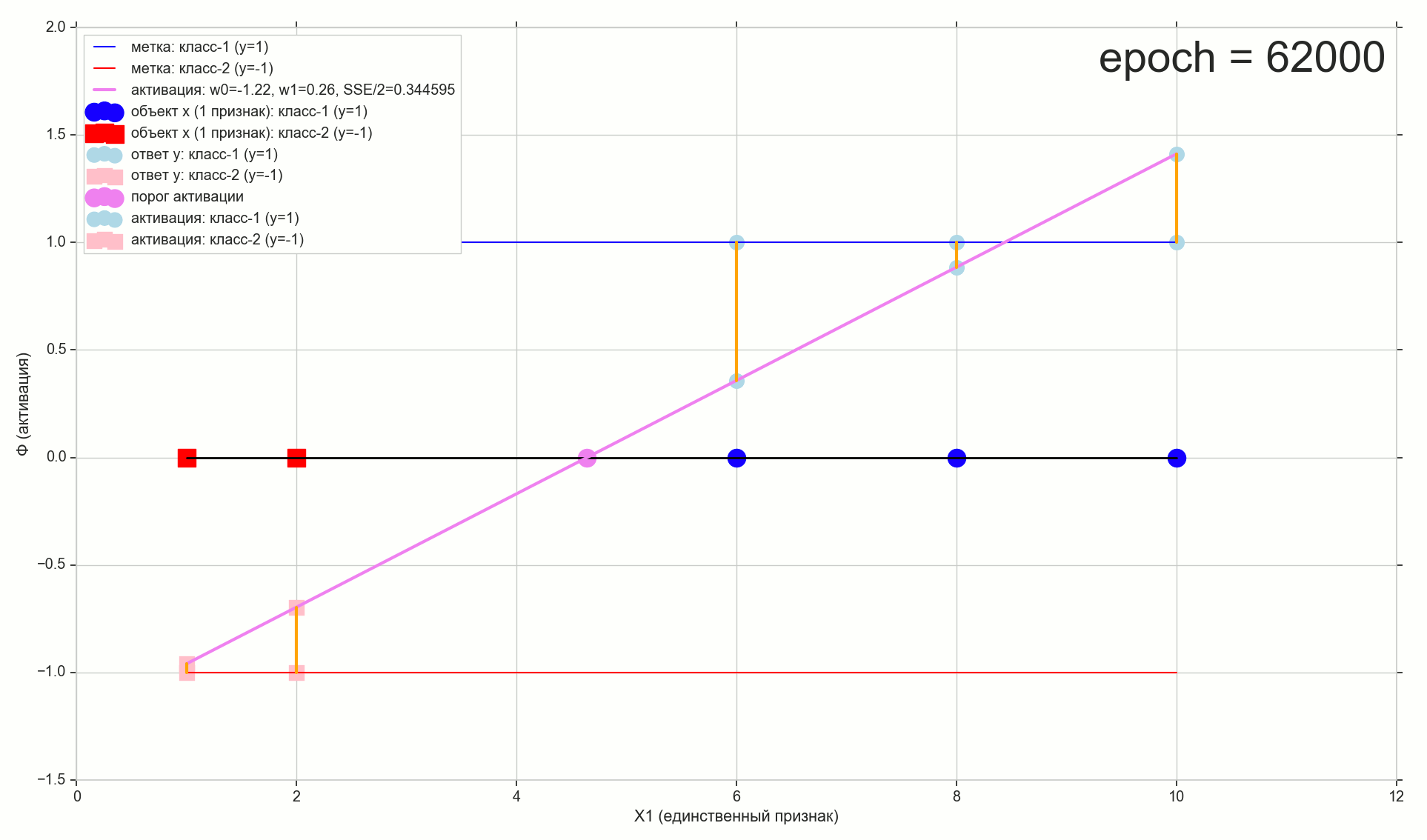
. , , , , .
- η=0.001 , 10-12- ( )
- , , , (1767)
- — 60
- —
— ( , 1767): w0=−1.184831 , w1=0.258455 .
.
t(1)=(t(1)1)=(1.4) ( , t(i) — ). , .. , , ˆy=−1 , .. .
SUM=w0+w1∗t(1)1=−1.18+0.26∗1.4=−0.816
Φ(SUM)=SUM=−0.816
Φ(SUM)=−0.816<0⟹ˆy=−1
, .
: t(2)=(t(2)1)=(7)
Φ(SUM)=SUM=−1.18+0.26∗7=0.64⩾0⟹ˆy=1
ˆy=1 , .. . .
, ( «» ) 12 . , !
(m=2)
, , , . . , , .
— ( ). 2- .
- x=(x1,x2) ( , , )
- y={−1,1} ( , )
plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1')

, .
Φ(x,w)=w0+w1x1+w2x2
, — , , 1- , 3-:

:

:

— :

() Φ(w)=0 (-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).
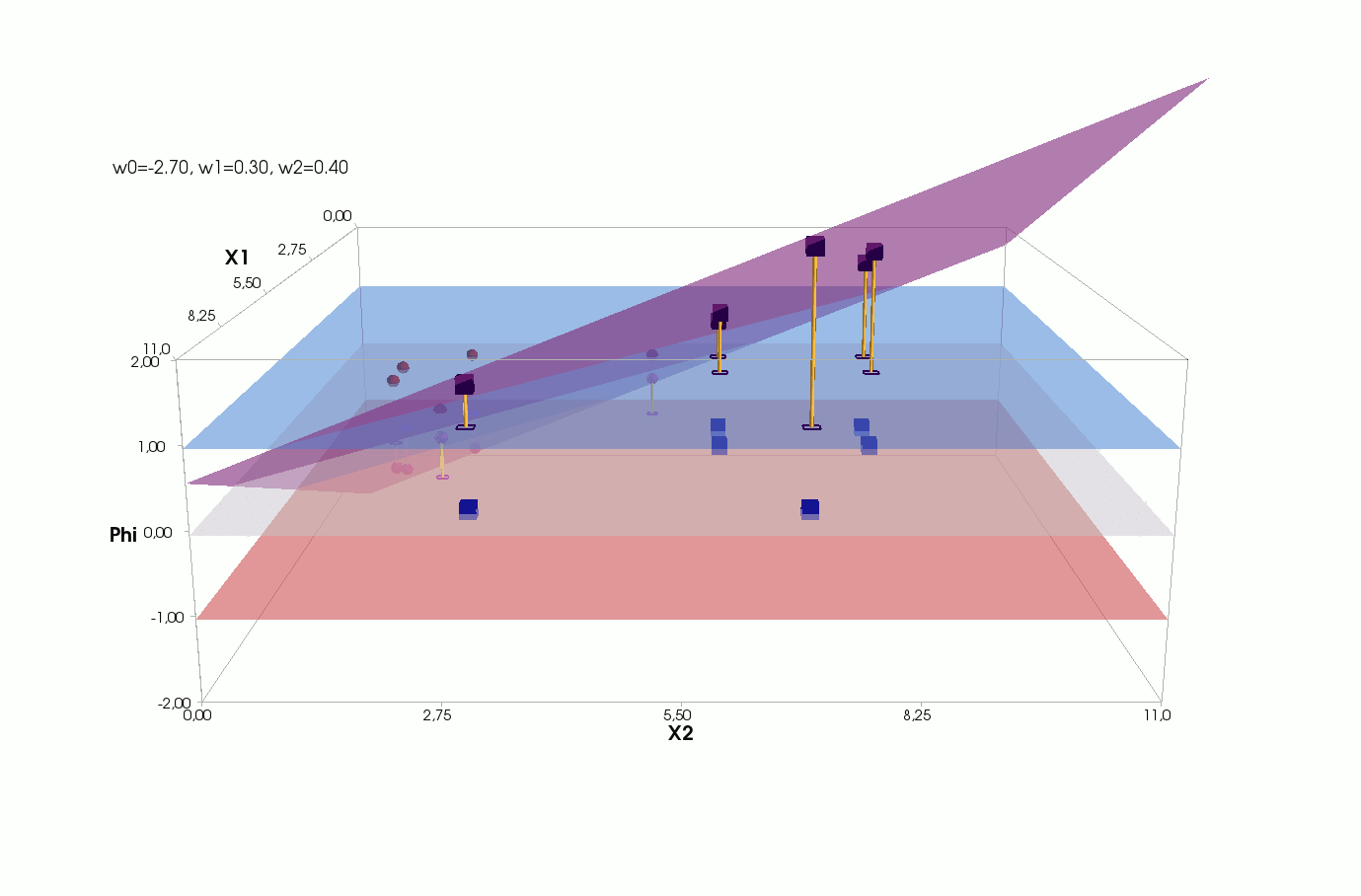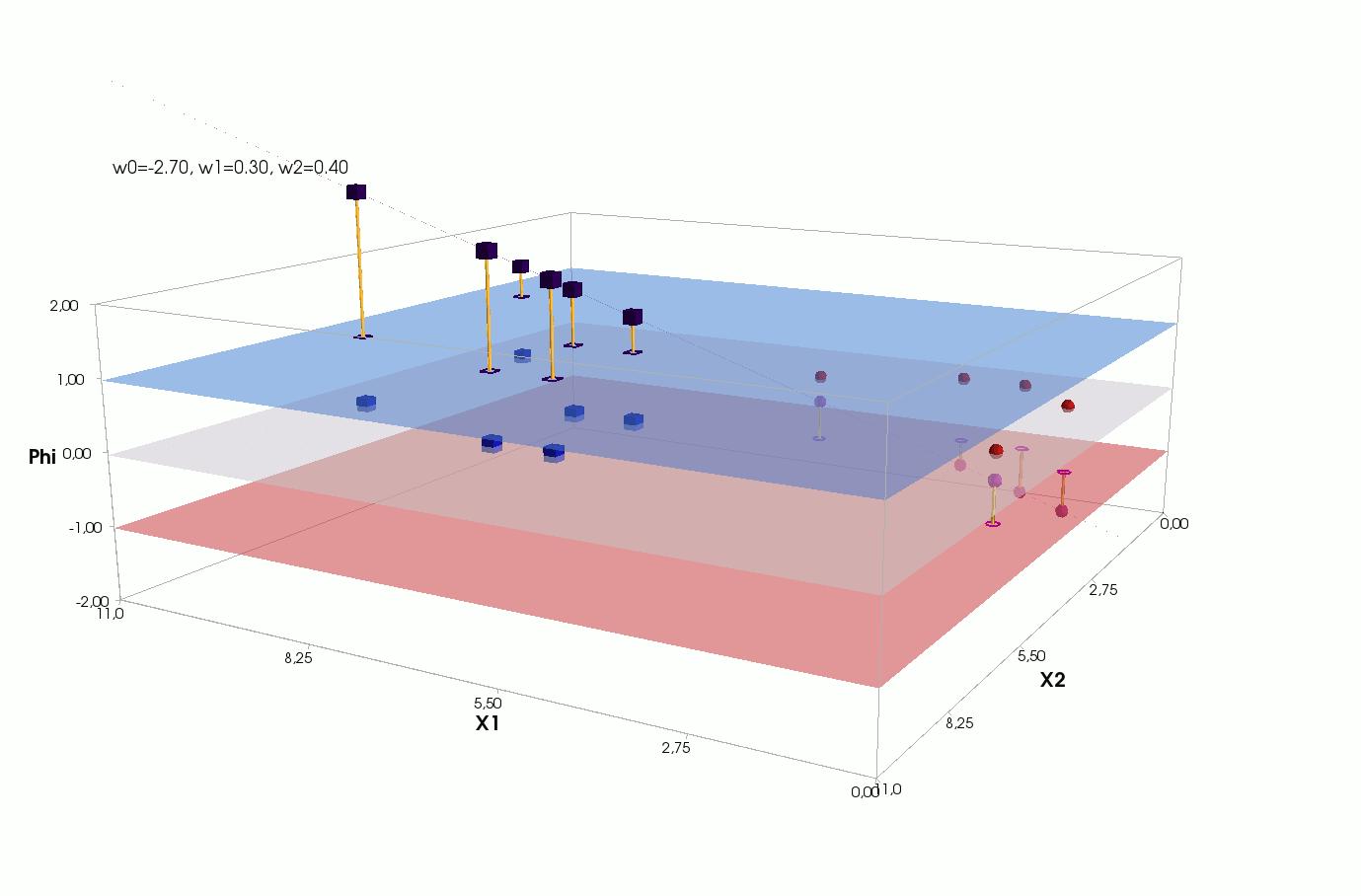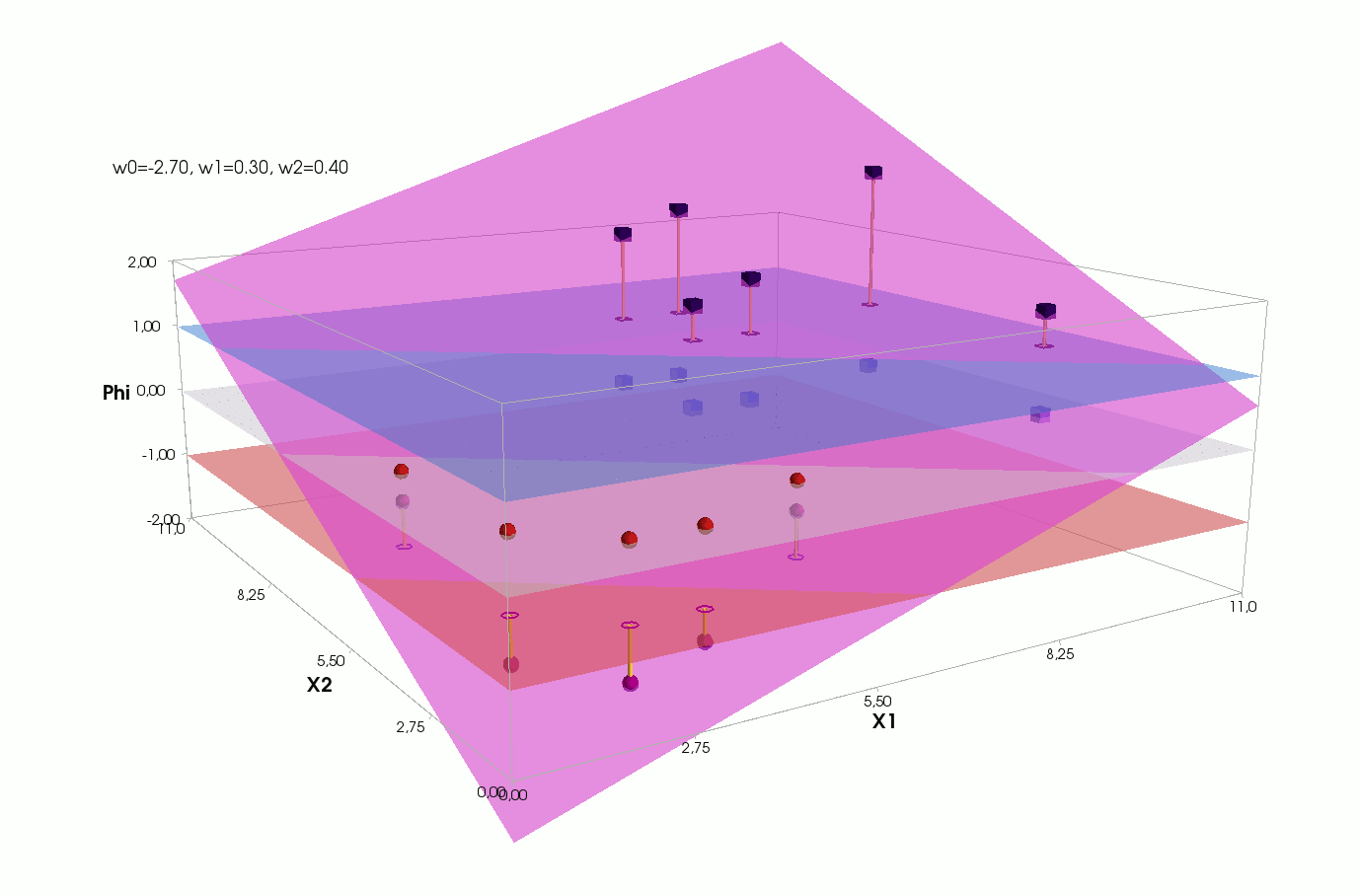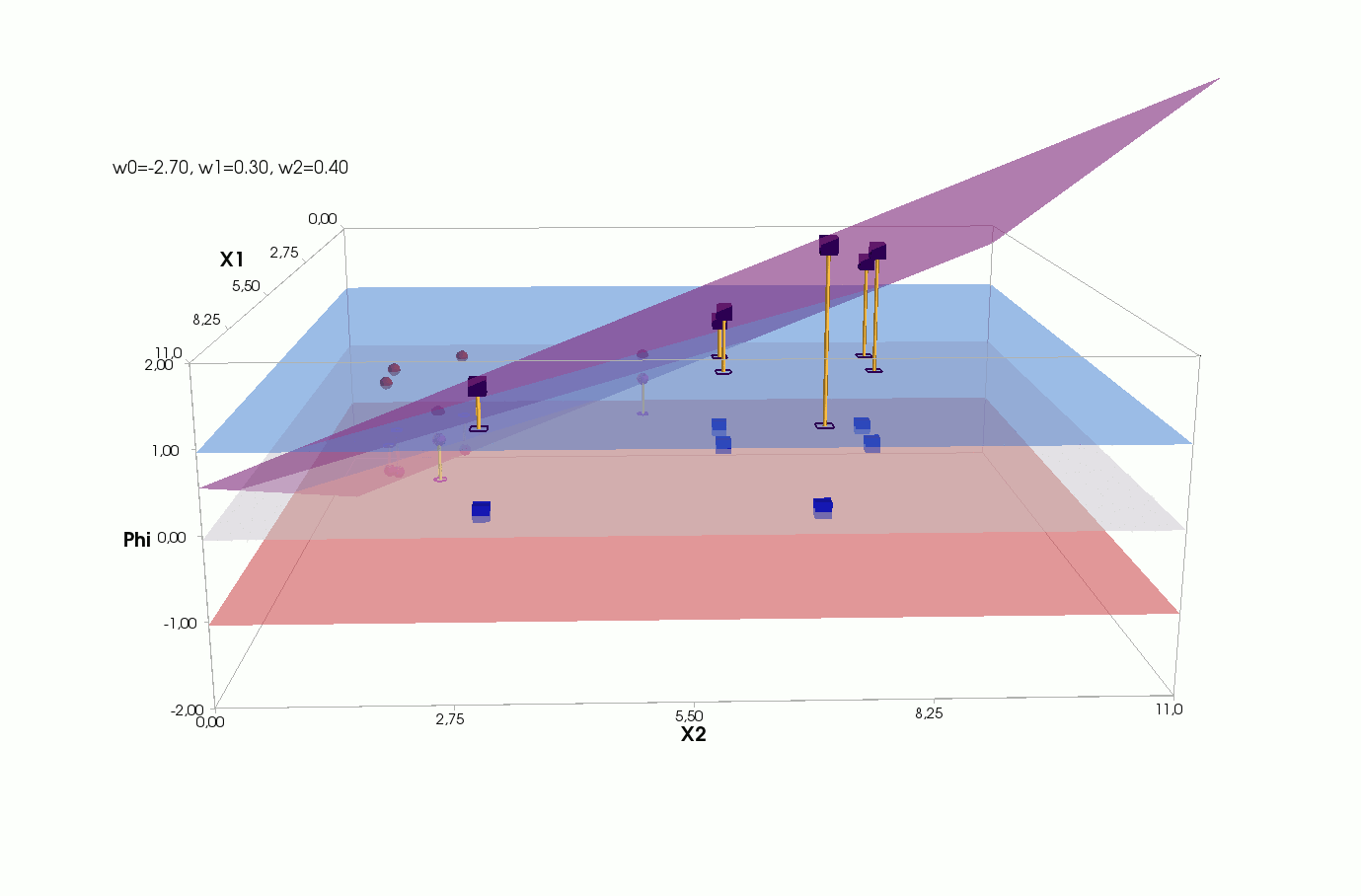
J(w)=12SSE=12n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))2
() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .
2- . , , 1- 2-.
∇J(w)=(∂J(w)∂w0,∂J(w)∂w1,∂J(w)∂w1),w=(w0,w1,w2)
( ):
∂J(w)∂w0=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
∂J(w)∂w1=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
∂J(w)∂w2=n∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
:
Δw0=−η∂J(w)∂w0=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))
Δw1=−η∂J(w)∂w1=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)1
Δw2=−η∂J(w)∂w2=−ηn∑i=1(w0+w1x(i)1+w2x(i)2−y(i))x(i)2
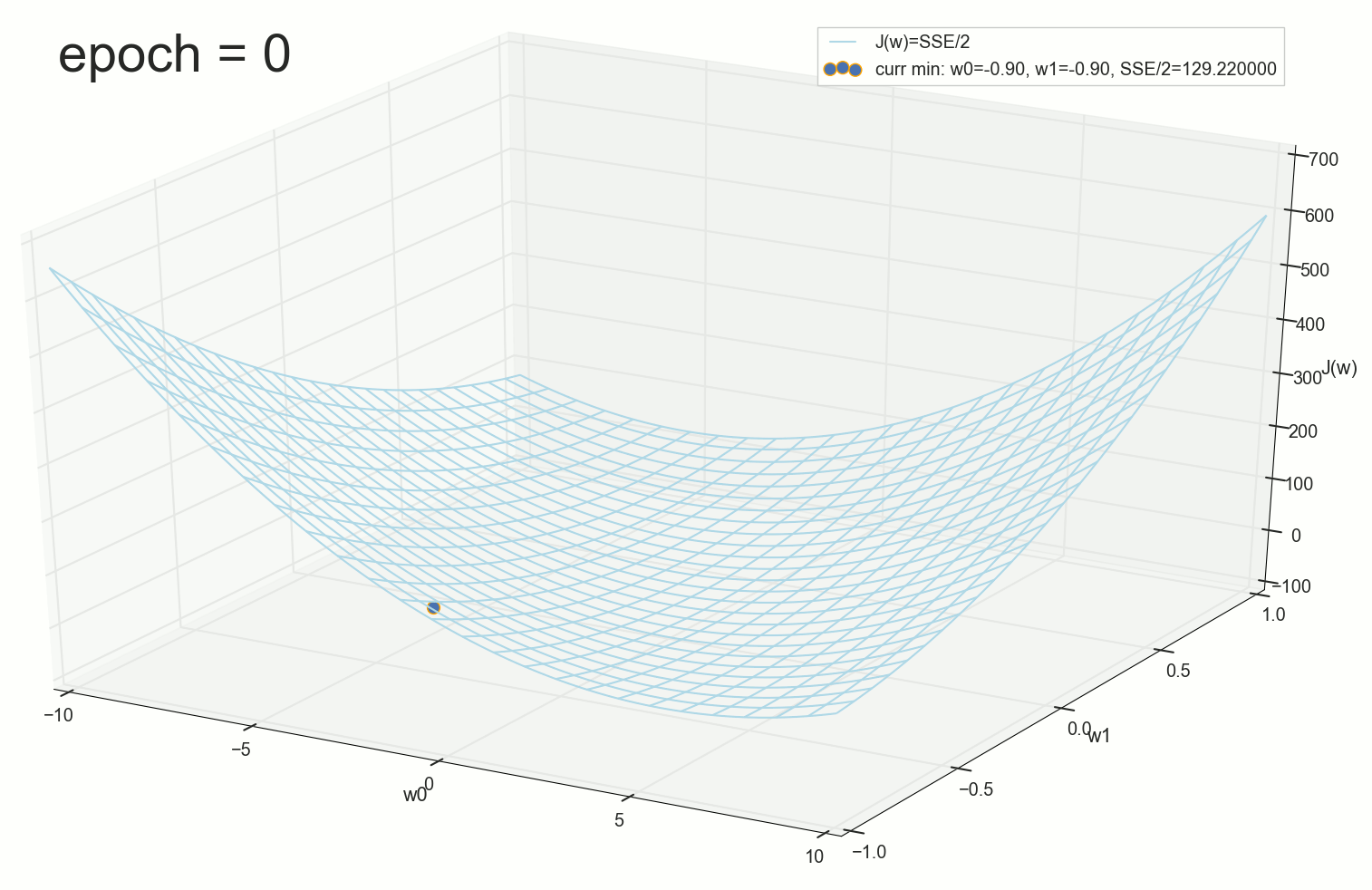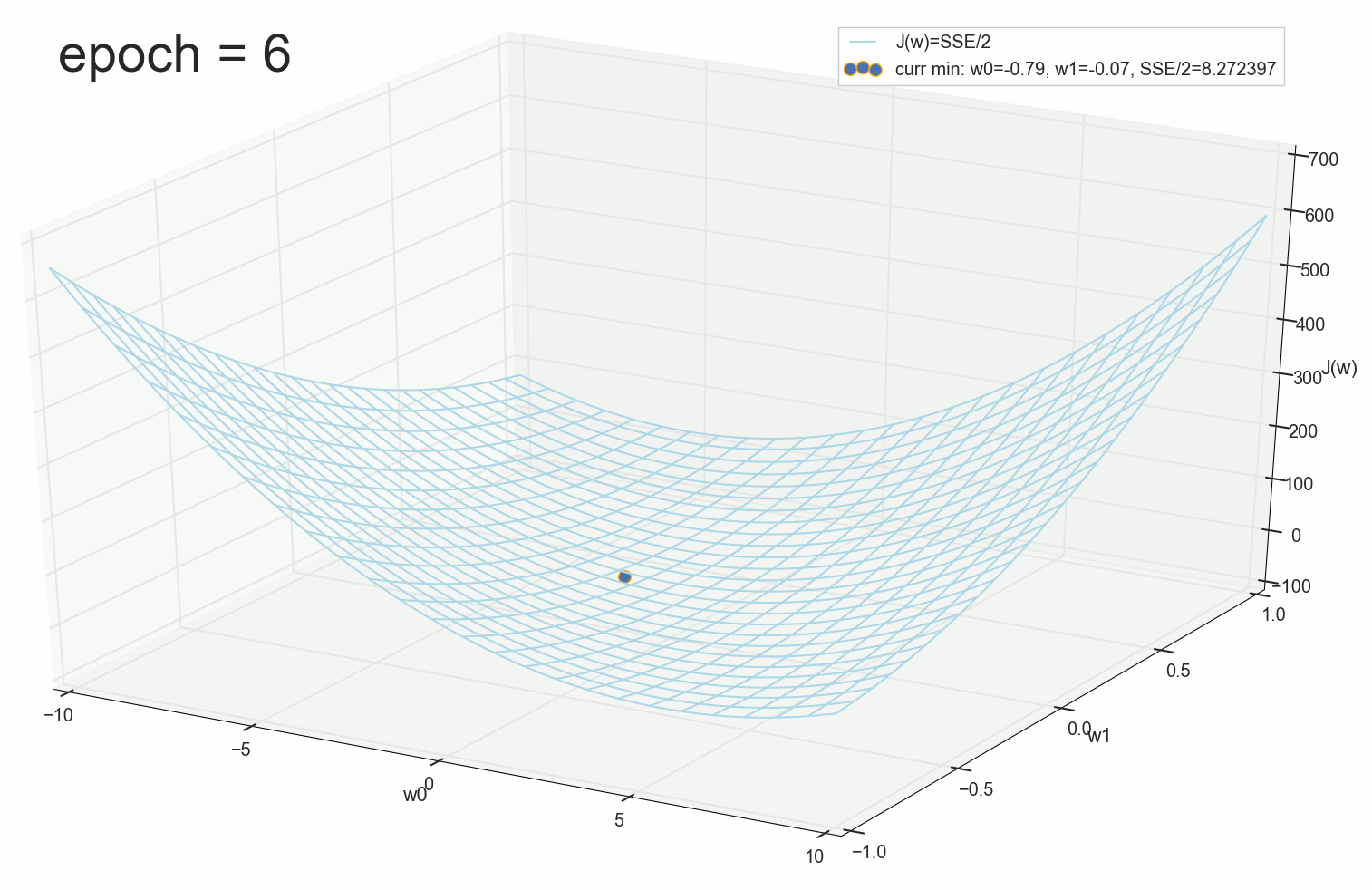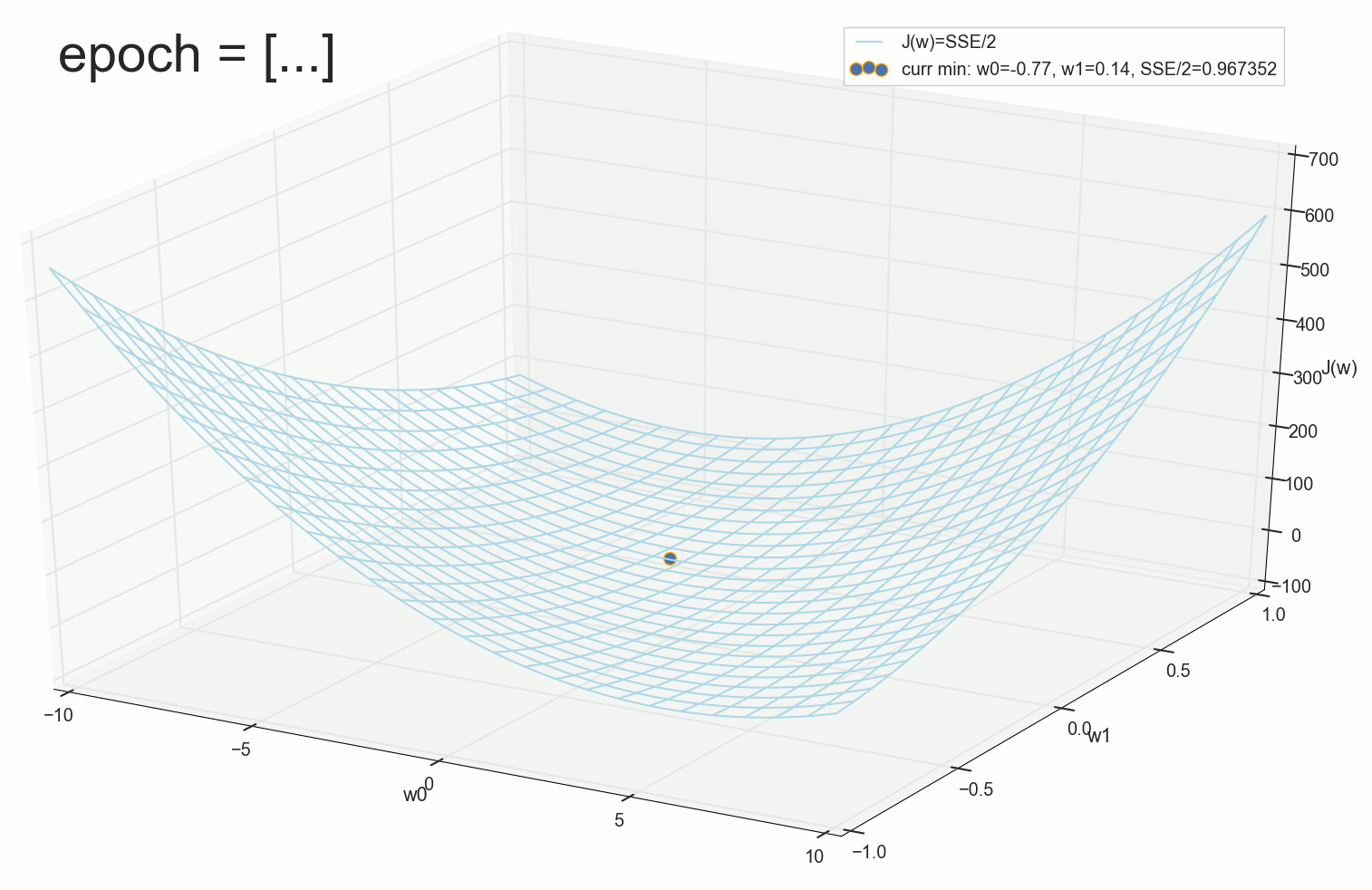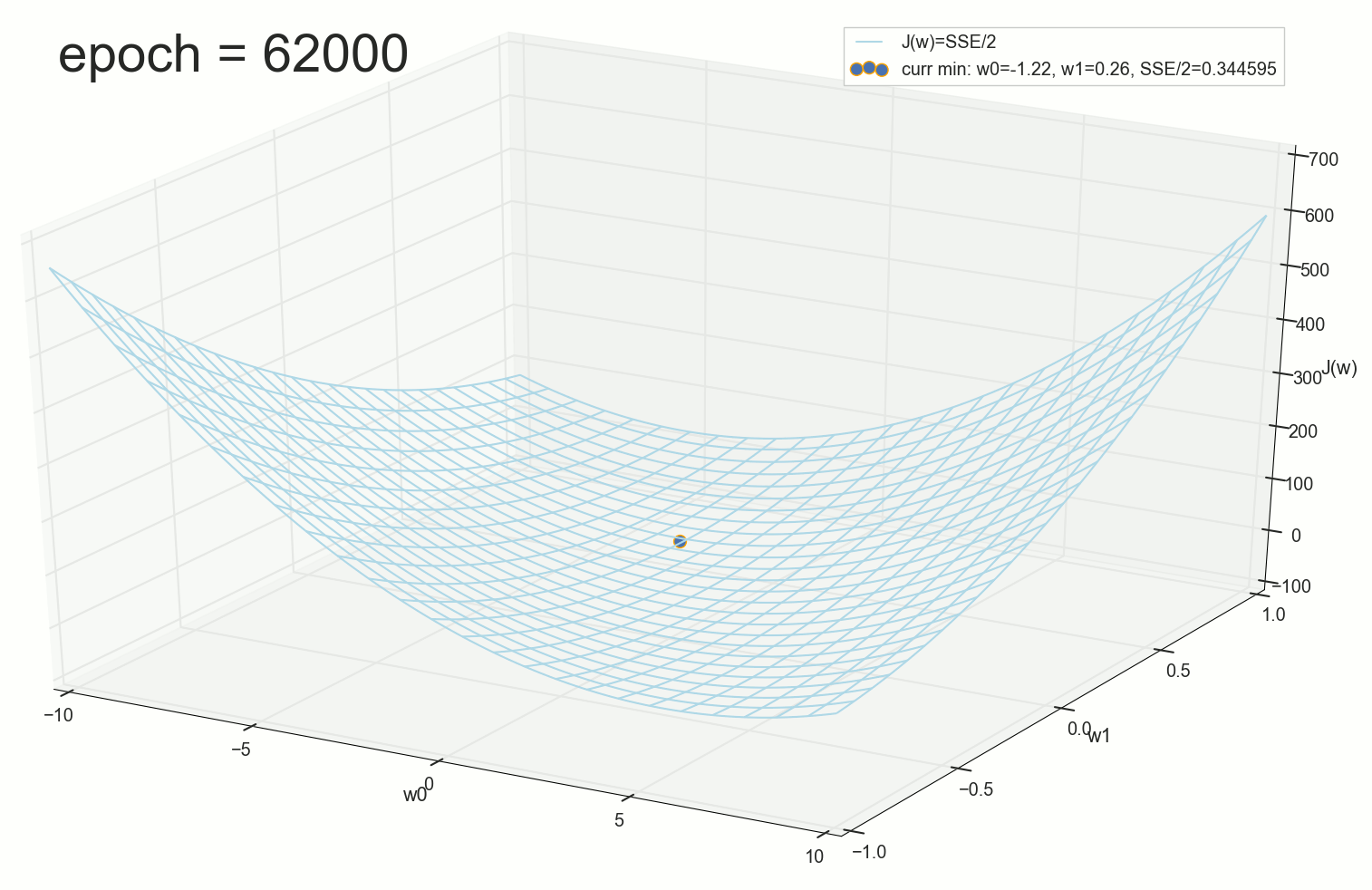
3- ( 3- ), η=0.001 , w0=−0.9 , w1=−0.9 , w2=−0.9 .
— , , :


:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , w0 .
Kode
matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .
import numpy from mayavi import mlab
, Mayavi , . , , , .
Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :
env QT_API=pyqt python3 gradient-2d.py
— J(w)
def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum()
12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .
Kesimpulan
ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .
«Python » ( scikit-learn) , - .
ADALINE .
-, — , : , , , .
-, () , , , ( , , y ) — , scikit-learn.
PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .