Hanya divisi, atau cara membuat teori matematika dan dapatkan $ 400K di atasnya. Seri dua, kedua dari belakang

Dalam seri sebelumnya , kami memeriksa bilangan pecahan yang tidak termasuk bilangan rasional. Hari ini, justru inilah, bukan bagian yang dianggap, yang menunggu kita, dan kita juga akan mempersiapkan bagian akhir yang sedikit lebih rumit tanpa menggunakan istilah seperti cincin kelas residu atau modulo perbandingan dengan logaritma diskrit. Juga di bagian ketiga dari mereka yang tertarik, hadiah $ 400 ribu sedang menunggu. Kenapa di yang ketiga? Karena tanpa pengantar subjek, tidak selalu mudah untuk memahami alasan mengapa hadiah tidak mudah didapat. Dan setelah membaca - hanya keberuntungan dan aktivitas yang bertujuan, sabar, tetapi tidak terlalu sulit, itulah yang Anda butuhkan.

Bintang yang rasional

Untuk menjawab pertanyaan yang diajukan sebelumnya tentang bilangan rasional, kita perlu penyimpangan kecil lagi. Pertama, ingatlah bahwa dalam proses membagi dengan "sudut" kita terus-menerus mendapatkan sisanya dari membagi bagian tertentu dari nomor dividen oleh pembagi. Dalam hal ini, seluruh bagian dari divisi ditulis ke dalam hasil, dan sisanya dari divisi dikalikan dengan basis sistem bilangan, setelah itu prosedur pembagian dengan sisanya diulang sampai periode terdeteksi atau semua faktor pembagi berkurang dan kita mendapatkan fraksi akhir.

Ini terlihat seperti ini:

5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... 

Di sini, sisa pengurangan 18 dari 20 selalu sama dengan dua, yang kemudian kita kalikan dengan basis sistem angka desimal.

Sekarang mari kita pikirkan bagaimana pembagian 5 dengan 3 berbeda dari, misalnya, pembagian 1 dengan 3? Jawabannya sederhana - kehadiran bagian integer sebagai hasilnya. Tetapi kami bertanya-tanya tentang periode dan bagian yang berjalan sebelum periode (disebut pra-periode), tetapi tidak termasuk dalam seluruh bagian dari hasil. Karena itu, kita tidak perlu mempertimbangkan keseluruhan bagian. Oleh karena itu, dalam contoh ini, semua angka yang lebih besar dari 3 atau sama dengan itu dapat dikecualikan dari pertimbangan. Dan yang bahkan lebih menarik - hukum pembagian dimanifestasikan dalam banyak hal tanpa angka lain kecuali satu. Artinya, cukup mempelajari pembagian suatu unit menjadi serangkaian bilangan bulat, yang besar, dan kita akan mengerti bagaimana menjawab semua pertanyaan yang diajukan, dan pada saat yang sama kita akan bertemu dengan jumlah bintang baru yang sangat baik.

Sementara itu, kami belum memulai studi serius tentang subjek - beberapa trik. Apakah Anda tahu bahwa berbagi dapat dilakukan "sebaliknya"? Tidak seperti kita terbiasa dari sekolah, tetapi mulai dari akhir. Mari kita tunjukkan ini dalam contoh lain, di mana kita mengambil sisa terakhir dan, mulai dari itu, kita menghitung periode fraksi. Ingat bahwa sisa pembagian 5 dengan 3 sama dengan 2. Berapa angka terakhir yang kita kurangi untuk mendapatkan deuce? Kita tidak perlu mengingat, karena kita tahu bahwa kita selalu mengurangi angka dari sisa sebelumnya dikalikan dengan 10, yaitu, digit terakhir dari pengurangan selalu sama dengan 0. Ini berarti bahwa cukup untuk memilah-milah produk triple dengan angka dari 1 hingga 9, = (3,6 , 9,12,15,18,21,24,27), untuk melihat - di antara mereka, hanya satu berakhir dengan 8 dan, secara total dengan sisanya 2, memberikan nol pada digit terakhir dari yang dikurangi. Jadi sebelum kita mendapatkan sisa 2, kita mengurangi 18 dari 20. Mengapa dari 20? Karena angka lain dengan nol di digit terakhir akan memberikan perbedaan X0-18 lebih dari tiga atau kurang dari nol. Dengan cara yang sama, kami menghitung semua angka lainnya:

2 - residu yang diketahui
18 - Selain nomor dengan nol, secara bersamaan menunjukkan nilai digit berikutnya sebagai hasilnya - 6 (6 * 3 = 18)
20 adalah angka yang cocok dengan nol
2 - angka dengan nol sebelum dikalikan dengan 10 (= 20/10)
18 - Selain nomor dengan nol
20 adalah angka yang cocok dengan nol
...

Akibatnya, kami mendapatkan urutan yang sama persis seperti ketika membelah oleh sudut, tetapi "di sisi lain." Jadi Anda dapat menghitung "dari akhir" periode dari setiap pecahan periodik. Dan apa pra-periode (dan tidak relevannya perhitungan untuk kasus ini dengan cara yang ditunjukkan) kita akan melihat lebih jauh. Seluruh bagian dari hasilnya selalu nol ketika menggunakan unit sebagai dividen, jadi sekali lagi kita kehilangan kebutuhan untuk menghitung sesuatu selain periode.

Sekarang ingat bagaimana kita membagi unit menjadi tiga: $$$1/3 = 0,3 (3)$ . Semuanya sederhana di sini, periode singkat, tidak ada pra-periode, sepertinya tidak ada yang luar biasa. Tapi mari kita coba gandakan hasil divisi ini menjadi tiga: $$$0,3 (3) * 3 = 0,9 (9)$ itu adalah $$$0,9 (9) /3=0,3 (3)$ . Dan pada awalnya seperti ini: $$$1/3 = 0,3 (3)$ . Tidak memperhatikan perbedaannya? Ada satu di input, dan setelah tindakan langsung dan terbalik, kita dapatkan ... Bagaimana saya bisa menyebutnya lebih mudah? Yaitu, jika kita melacak seluruh rantai sembilan hingga tak terhingga, maka kita akan mengerti bahwa kita memiliki satu unit, tetapi tetap saja entah bagaimana tidak seperti itu, dapatkah Anda menemukannya? Ya, tidak seperti aslinya, dan hanya itu. Matematikawan akan mengatakan bahwa ini hanyalah dua bentuk notasi dengan angka yang sama, tetapi pemahaman sehari-hari tentang "yang sama" sedikit memberontak terhadap definisi semacam itu. Pada prinsipnya, sulit untuk tidak setuju dengan ahli matematika, karena banyak sembilan setelah titik desimal berbeda dari kesatuan dengan sesuatu yang benar-benar fana, sangat kecil dan cenderung nol dalam batas. Tetapi secara khusus, dapatkah Anda menjaring seluruh rangkaian infinitas dengan pikiran Anda? Jumlah yang tidak terbatas dari sembilan, perbedaan yang sangat kecil, cenderung ke nol ketika bergerak sepanjang serangkaian sembilan hingga tak terbatas. Dan sekarang bandingkan ini dengan catatan seperti itu - 1. Satu tanda - dan semuanya jelas bagi kita. Dan berapa banyak tanda yang ada dalam diskusi tentang kesetaraan jumlah yang tidak terbatas dari sembilan menjadi satu? Artinya, masih ada perbedaan? Atau apakah otak Anda dengan mudah mengabaikan hal-hal sepele dalam serangkaian perbedaan? Tetapi jika kita tidak pergi ke pandangan mental yang tak berujung dalam daftar sembilan, maka di tempat di mana kita berhenti, akan segera ada perbedaan yang bahkan matematikawan mengakui sebagai signifikan - jika Anda tidak melihat kesembilan yang lain, maka kita tidak sama sekali. Karena itu, muncul pertanyaan - dapatkah Anda melihat sampai ke kedalaman semua ketidakterbatasan? Secara umum, apa pun yang Anda inginkan, matematikawan telah memerintahkan fenomena ini untuk dianggap nomor yang sama. Karena itu, setelah mempertimbangkan bintang ini (dengan kejujuran - cahaya aneh), kita beralih ke bintang berikutnya.

Kesimpulan yang menarik mengikuti dari fakta mendeteksi jumlah sembilan yang tidak terbatas - jika pembagi kesatuan adalah prima lebih besar dari 3, maka periode yang dihasilkan selalu dibagi dengan 9, dan tentu saja dengan 3, dan juga dengan panjangnya lebih dari satu karakter - oleh 11, dan ketika lebih banyak karakter - 13, 37, 101, dan seterusnya. Dan ini semua terlepas dari pembagi unit, kalau saja itu sederhana dan lebih dari tiga. Anda dapat memeriksanya sendiri, misalnya, membagi periode 1/7 sama dengan 142857 dengan 3, 9, 11, 13, 37.

Nah, sebelum tumpukan kita mengajukan pertanyaan sederhana - apakah mungkin untuk membangun periode sendiri? Ya kamu bisa. Misalnya, kita ingin mendapatkan periode 0123456789, dapatkah kita menemukan dividen dan pembagi yang memberikan sesuatu yang serupa? Kamu bisa! Tetapi tanpa angka 8. Maka itu akan menjadi 1/81. Dan agar angka 8 muncul di tempat yang semestinya, kita perlu menambahkan ke angka 81 beberapa digit setelah titik desimal, atau tanpa titik desimal, tetapi kemudian banyak nol akan hadir pada periode tersebut.

Keteraturan lain - untuk beberapa pembagi satuan, kita tidak dapat menghitung periode sama sekali, tetapi cukup menggesernya secara siklikal ketika kita mengalikan dividen (unit) dengan nomor berapa pun. Misalnya - 1/7 = 0. (142857), dan 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) dan seterusnya. Jika dividen lebih besar dari 7, maka seluruh bagian dari hasil pembagian akan pergi ke bagian sebelum titik desimal, dan periode akan tetap terdiri dari enam digit yang sama, tetapi sekali lagi bergeser secara siklis - 25/7 = 3. (571428), 86/7 = 12. (285714) dll. Bagaimana kamu suka itu? Angka apa pun ketika dibagi 7 memberikan satu set angka yang sama! Apapun! Benar-benar ada Dan ya, "angka apa saja" ini adalah angka yang tak terbatas. Dan hasilnya selalu termasuk 6 dari angka yang sama. Selanjutnya, Anda akan memahami mengapa dunia angka sangat terstruktur, tetapi untuk saat ini, kami mencatat bahwa ketika membagi unit dengan 7, kami secara implisit menerima semua informasi yang diperlukan untuk menghitung periode dari hasil angka lainnya menjadi tujuh, karena kami sekarang tahu bahwa itu cukup hanya untuk menggeser secara siklis satu. satu-satunya hasil dari divisi. Artinya, sekali lagi dikonfirmasi bahwa tidak perlu berurusan dengan pembagian angka apa pun, kecuali satu, dengan nomor yang dipilih untuk penelitian. Benar, mungkin perlu untuk mengalikan dengan beberapa angka dan mengingat hasil antara, tetapi lebih lanjut tentang itu nanti.

Sekarang untuk tampilan yang lebih umum, kami akan menunjukkan "peta pertempuran". Sebuah peta digambar untuk membagi unit dengan angka yang diteliti, sementara pembagian dilakukan di semua sistem angka dengan basis lebih sedikit dari angka yang diteliti. Peta tidak termasuk hasil pembagian, yaitu periode fraksi yang dipermasalahkan, melainkan peta yang berisi residu yang diperoleh pada setiap tahap pembagian dengan “sudut”. Begini tampilannya:


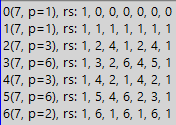
Pada tabel di atas Anda melihat garis, dari 0 hingga 6. 0 juga merupakan dasar untuk sistem angka. Apakah Anda tidak setuju? Mari kita coba meyakinkan. Apa itu sistem angka? Ini adalah basis, dikalikan dengan nilai tertentu, dan kemudian ditambahkan ke hasilnya, yang pada awalnya adalah nol. Jadi semua angka diperoleh, misalnya, dalam sistem angka desimal. Dan jika basisnya nol? Maka semua istilah yang dikalikan dengan nol juga akan sama dengan nol. Tapi apa yang berubah? Sudahkah kita melanggar aturan membangun angka dalam sistem angka yang dipilih? Oleh karena itu, untuk gambaran umum pada peta pertempuran, kami menggunakan semua sistem bilangan, dari 0 hingga 6 dalam hal mempelajari angka 7. Tetapi selain generalisasi, garis dengan nol akan memiliki tujuan tambahan.

Tapi apa arti semua baris ini? Setiap baris menunjukkan kepada kita urutan residu ketika membagi unit dengan tujuh dalam sistem angka, yang ditandatangani di kolom paling kiri. Yaitu, ketika membagi 1/7 dalam sistem dengan basis 0, kita memiliki sisa awal 1 (unit yang kita bagi). Selanjutnya, seperti yang selalu kami lakukan ketika membaginya dengan sudut, kami mengalikan sisa pertama dengan basis sistem bilangan. Kami mendapat nol. Sekarang nol adalah sisa saat ini. Biasanya, ketika menghitung hasil bagi setelah menerima sisa sama dengan nol, dan jika tidak ada angka tambahan dalam angka yang dapat dibagi, pembagian dihentikan (karena hasilnya diperoleh). Tetapi dalam kasus kami, kami mengisi tabel yang tidak mentolerir kekosongan, dan selain ketidaksabaran, ia memiliki sifat tambahan yang juga membutuhkan keberadaan angka dalam semua sel. Oleh karena itu, kami terus membagi dan membagi sisa 0 dengan 7. Biasanya, sementara sisanya lebih kecil dari pembagi, itu dikalikan dengan basis sistem bilangan, tetapi mengalikan dengan nol berkali-kali tidak berguna, jadi kami hanya menulis bahwa setelah mengalikan dengan nol sisanya menjadi nol lagi, dan Sekarang letakkan di meja di sel berikutnya. Kemudian ulangi prosedurnya. Jadi kami mengisi semua sel di baris pertama dengan nol. Dan kemudian isi baris kedua. Tetapi sudah memiliki dasar lain dari sistem angka - unit. Setelah membagi 1 dengan 7, kita memiliki sisanya pertama - satu. Lalu kita kalikan dengan basis sistem bilangan, yaitu dengan satu. Kami mendapat lagi 1. Kami menulis di sel yang sesuai. Sekali lagi kita kalikan dengan 1, lagi kita mendapatkan 1, kita menulis lagi. Demikian seterusnya hingga baris kedua terisi. Tetapi setelah dua garis yang indah ini dalam segala hal, kita akhirnya sampai pada pembagian yang lebih bermakna - dalam sistem biner (dan makna dari dua sistem pertama akan menjadi jelas nanti). Pertama, kita memiliki unit yang sama. Tulis unit di baris ketiga. Kemudian kita kalikan dengan basis sistem bilangan (dengan 2). Kami mendapat 2. 2 kurang dari tujuh, kami belum bisa mengurangi, jadi kami menulis sisanya 2 di tabel. Sekali lagi, kita kalikan dengan 2, kita dapatkan 4, yang lagi-lagi kurang dari 7, jadi sekali lagi ia pergi ke meja tanpa perubahan. Tetapi pada langkah berikutnya kita mendapatkan 8, yang lebih dari 7, jadi kita perlu mengurangi. Hasilnya adalah 1. Kami menulis di tabel. Tetapi sebelumnya kita sudah memiliki satu unit, jadi semua langkah lainnya akan sama - jadi kita akan menambahkan baris ketiga ke akhir. Dan dengan cara yang sama kita akan menambahkan sisa baris, tetapi tidak lupa bahwa kita perlu mengalikannya dengan basis lain dari sistem angka.

Jadi, ketika kita akhirnya mendapatkan tabel yang lengkap, kita bisa menarik beberapa kesimpulan. Pertama, perhatikan pengulangan. Untuk sistem biner, kami memiliki 1,2,4,1,2,4,1, yaitu, dua kali 1,2,4 dan kemudian satu kali lagi 1. Di sini, daftar 1,2,4 sesuai dengan periode fraksi biner yang dihasilkan. Artinya, periode akan menjadi panjang 3. Dan meskipun kami menggunakan sisanya sebagai ganti angka dari periode, panjangnya tidak menderita karena ini, dan oleh karena itu semua informasi disimpan. Dan bahkan lebih - dalam tabel benar-benar ada lebih banyak informasi yang tersisa. Tetapi lebih lanjut tentang itu nanti, tetapi untuk saat ini, kami mencatat bahwa semua garis dibuat dengan panjang yang sama untuk kemudahan belajar dan karena adanya sejumlah properti yang bermanfaat. Jadi, garis-garis dimulai dan diakhiri dengan satuan-satuan, yang membedakan dengan baik sifat-sifat angka 7. Dan jika kita mengurangi garis-garis pada panjang periode, kita tidak akan dapat menikmati keindahan tampilan simetris esensi dari angka 7.

Sekarang tentang informasinya. Saldo secara tidak ambigu mengatur angka pada posisi yang sesuai pada periode tersebut, oleh karena itu informasi dalam representasi ini tidak hilang, tetapi karena saldo dapat lebih besar, misalnya, maksimum satu posisi desimal (mis. 9), informasi dengan partisipasi mereka menjadi yang paling lengkap, karena satu posisi dalam sistem perhitungan tidak dapat memberi tahu kami bahwa sisanya adalah, misalnya, 19, tetapi sisanya 19 akan dengan jelas memberi tahu Anda apa angka dalam periode dan dari yang sebelumnya kami mengurangi produk dividen (ingat fokus dengan pembagian "dari akhir"). Dan selain itu, kami segera memperhatikan satu hal sederhana - tidak ada residu lagi $$$N-1$ dimana $$$N$ - nomor yang diselidiki dimana kami membagi unit. Ini adalah poin yang sangat penting. Selain itu, dapat dengan mudah dibuktikan bahwa jika residu yang sebelumnya ditemui diulang ketika membaginya dengan sudut, maka akan ada pengulangan dari seluruh urutan residu yang mengikuti nilai yang diulang sebelumnya. Jadi kita tidak perlu mengambilnya lagi, begitu periode ditemukan. Jika kita hanya mencatat angka-angka dari periode, maka pengulangan angka-angka dalam periode tidak berarti penyelesaian perhitungan. Oleh karena itu, saldo lebih penting daripada angka dari periode tersebut. Tapi yang paling menarik adalah sisa-sisa segalanya $$$N-1$ , dan karena itu periode lebih lama $$$N-1$ tidak mungkin. Jadi, di sini kita baru saja menemukan batas atas jumlah digit pada periode tersebut, bergerak dari digit aktual periode ke saldo. Seperti yang mereka katakan, gerakan tangan mudah dan tidak ada penipuan. Ini adalah manfaat dari informasi yang lebih lengkap. Nah, oleh karena itu, lebar "peta pertempuran" kami untuk 7 pertandingan adalah 6 + 1 kolom, yaitu, 6 kolom untuk semua kemungkinan residu dan 1 kolom untuk mendeteksi simetri dari unit, yang sama sekali tidak wajib untuk semua angka, dan oleh karena itu tidak wajib Layak disembunyikan, menghemat ruang di bawah satu kolom.

Nah, sekarang lihat "peta" di atas dalam hal kegunaannya. Anda dapat segera melihat serangkaian pola sederhana. Setiap baris dimulai dengan satu unit, dan berakhir dengan itu. Posisi kedua dari setiap baris menunjukkan basis dari sistem angka, tetapi bagian tengah dari setiap baris mengandung N-1 atau 1. Perhatikan bahwa kami tidak melakukan upaya apa pun untuk mengatur angka dalam tabel dalam urutan ini, kecuali hanya memperbaiki hasil pembagian dalam tabel. Namun terlepas dari kami mengabaikan urutan apa pun (kecuali untuk urutan langkah-langkah pembagian), urutan itu sendiri muncul entah dari mana dan menarik kita huruf P dari unit, mengenakannya topi nol (dengan pelindung dari satu), membagi meja dengan kolom tengah unit, dan penambahannya ke angka 7 (sesuai dengan rumus 7-1 = 6). Selain itu, urutan itu sendiri menempatkan sistem angka di kolom kedua. Bandingkan dengan angka-angka di kolom kiri pertama, mereka hanya ditambahkan secara sengaja, sehingga kita tahu persis di mana sistem angka itu. Yah, kita dapat dengan mudah menghitung periode fraksi yang dihasilkan sendiri, meskipun untuk kenyamanan itu ditunjukkan dalam kolom dengan nilai-nilai bentuk p = X.

Sebenarnya, sebelum Anda adalah sesuatu seperti tabel periodik, tetapi tidak untuk kimia, tetapi untuk teori bilangan. Dengan cara yang sama seperti Mendeleev, Anda bisa melihat tabel menemukan pola tertentu, dan kemudian, seperti setelah Mendeleev, keberadaan pola ini dapat dibenarkan dan membuktikan bahwa itu diulang untuk semua angka yang memenuhi serangkaian kondisi tertentu. Dan ini adalah hal terpenting dalam tabel tersebut. Hanya dengan melihat dan mengamati pola, Anda dapat menemukan hukum, misalnya, teori bilangan. Nah, untuk pembaca yang lebih bijak, jalan menuju siklus penuh terbuka di sini - setelah menemukan pola, Anda perlu membuktikan (atau menyangkal) relevansinya untuk semua angka, atau untuk jumlah kelas tertentu.

Seperti dicatat, tabel ini berisi informasi lengkap tentang bilangan prima 7. Tetapi dari informasi ini kita dapat memperoleh hipotesis tentang semua bilangan prima. Dan bahkan beberapa dari hipotesis ini telah terbukti pada kita, jadi kita hanya perlu memeriksa kesimpulan dari yang lain. Bukti diberikan oleh orang-orang terkenal seperti, misalnya, Fermat dan Euler. Farm memberi kami formula ini $$$a ^ {(p-1)} \ pmod p = 1$ (di sini operasi mod mengambil sisa pembagian nilai di sebelah kiri dengan nilai di sebelah kanan, dalam pemrograman biasanya ditunjukkan oleh simbol%), yaitu sisa dari pembagian $$$a ^ {(p-1)}$ pada p selalu sama dengan satu untuk semua bilangan prima (yaitu bilangan prima, ini penting). Namun angka 7 juga prima. Dan setiap residu di setiap baris dapat dihitung menggunakan rumus berikut: $$$b ^ i \ pmod N = r$ . Di sini b adalah basis dari sistem angka (dari basis bahasa Inggris), i adalah nomor posisi di baris (dari indeks bahasa Inggris), mulai dari nol untuk posisi pertama, N adalah angka yang sedang diselidiki (dalam hal ini - 7), r adalah sisanya (dari pengingat bahasa Inggris) ) terbentuk pada langkah ke-i dari pembelahan oleh sudut dan terkandung dalam kolom ke-i dari tabel. Mari kita bandingkan rumus Fermat dan rumus untuk menghitung sisanya yang ditentukan oleh indeks i. Mereka identik untuk anggota terakhir dari semua urutan residu. Dan sesuai sepenuhnya dengan formula Fermat, untuk setiap sisa dalam posisi $$$N-1$ kami memiliki persamaan untuk persatuan. Artinya, pola yang diamati dengan mata telanjang dalam bentuk kolom unit dikonfirmasi dan dibuktikan kembali pada zaman Fermat (meskipun Fermat tidak memanjakan kita dengan bukti, tetapi biasanya semua pernyataannya benar). Euler menambahkan ke formula Fermat kemampuan untuk menggunakannya tidak hanya untuk bilangan prima, tetapi juga untuk bilangan komposit. Benar, Anda perlu tahu semua pembagi nomor, tetapi untuk jumlah kecil ini bukan masalah. Jadi pada tabel kedua (di bawah) kita melihat urutan residu untuk angka 21, yang merupakan komposit. Euler membuktikan bahwa sisa pembagian angka sewenang-wenang ke tingkat yang sama dengan jumlah angka yang lebih kecil dan tidak memiliki pembagi umum dengan N juga sama dengan satu. Dan justru fakta ini yang kita amati dalam tabel untuk angka 21, yang mana dari 20 angka yang lebih rendah, 8 memiliki pembagi umum dengan 21, dan 12 tidak. Oleh karena itu, kami mengamati di kolom ke-12 (saat pengindeksan dari awal) banyak unit. Dan unit-unit ini tidak berada di ujung garis, karena beberapa angka yang kurang dari 21 memiliki pembagi umum dengan 21. , , . — , . — 12- 21 . ? , , , , 3 7 ( 21) . , , , .


Meskipun perlu dicatat bahwa baik Fermat maupun Euler tidak tahu tentang tabel di atas. Dan jika mereka tahu, maka tidak ada yang diberitahu tentang dia. Meskipun, di sisi lain, di zaman mereka, notasi desimal alternatif agak kurang populer daripada di zaman kita. Kemudian bahkan tidak semua orang tahu tentang sistem desimal, tetapi mereka hanya menghitung dengan jari. Dan oleh karena itu, Fermat yang disimpulkan, dan kemudian formula yang diperpanjang oleh Euler untuk menghubungkan dasar dan tingkat, tidak memberi kita penjelasan tentang hukum lain dari tabel ini. Oleh karena itu, lebih banyak bintang menunggu kita, dan kemudian periode pembukaan kondisional dari kulit elektron, dengan bantuan ahli kimia yang akhirnya menjelaskan sifat prediktif magis dari tabel periodik. Tapi mari kita mulai dengan sihir.

Dari bintang ke sihir

« ». , , , . , . . , , , «». — , , . , . , , .

. . , , . 2 7 3, 6. 4 6, 24 mod 7 = 3, . ( ) , . 24, , 3. 1/7, , . ? .

Simetri Setiap kolom kedua berisi bagian atas dan bawah, yang merupakan cerminan satu sama lain. Dan kolom lainnya berisi nilai yang sama dengan komplemen dari saldo N yang direfleksikan. Artinya, pada kolom kedua tabel untuk angka 7, suplemen nomor 1 6 sampai 7, 2 suplemen 5 dan 3 suplemen 4. Akibatnya, rumusnya dipertimbangkan di atas$$b i( modN ) = r dilengkapi dengan sistem berikut:$b^i \pmod N = r$

$$( N - j ) i( modN ) = r , untuk kolom ganjil$(N-j)^i \pmod N = r$
$$j i( modN ) = r , untuk kolom genap$j^i \pmod N = r$
$$j = N - b Di sini N adalah angka yang sedang dipelajari (misalnya 7), b adalah dasar dari sistem angka, i adalah indeks kolom mulai dari nol, r adalah nilai sisa dalam sel b dan i yang diberikan.$j=N-b$



N. , . ( , ) , N . — . N, , N. ( ) $$( N - 1 ) / 2 (tanpa baris nol), dan semua nilai residual lainnya diturunkan secara jelas berdasarkan informasi dari bujur sangkar tersebut. Meskipun Anda tidak boleh lupa bahwa secara umum seluruh tabel berasal dari pengetahuan tentang satu nomor tunggal - pembagi, sedangkan dividennya adalah konstan sama dengan 1.Sekarang jumlahnya. Pada dasarnya untuk yang sederhana, tetapi terkadang untuk gabungan, aturan yang ditunjukkan di bawah ini diikuti. Jumlah horizontal (tanpa kolom terakhir ditambahkan untuk kejelasan) selalu merupakan kelipatan dari angka yang sedang diselidiki. Jumlah vertikal juga selalu merupakan kelipatan dari angka yang sedang diselidiki. Jumlah saldo dalam periode dari satu ke satu (periode tersebut mungkin kurang dari lebar tabel) adalah beberapa atau sama dengan jumlah yang sedang diselidiki.$(N-1)/2$



. ( ) , . , ( 21 7).

. , , — , N . , , — .

. , , , , . , , , , , . , ( ). «» , , , , .

, . , . — , , , — . , , ( , ). 7 , 7, , 1/7. 7 ( ) , , ( ), . — , . , 10 7 — 3. 3 , , , . , , . N . , , .

Dan beberapa ketergantungan antara berbagai angka yang dipelajari:


Di sini kita melihat baris untuk angka 2 hingga 39 dalam sistem biner. Perhatikan baris bawah. Kolom angka 1,2,4,8,16,32 naik dari itu. Setelah angka 32, kita melihat kolom nilai bertambah satu (25,26,27, ...). Di kolom berikutnya, nilainya meningkat tiga. Kemudian pada 6, 13, 26, dll. Peningkatan "beralih" setelah mencapai nilai yang lebih besar dari angka yang sedang diselidiki (kolom di sebelah kiri dalam tanda kurung, sebelum panjang periode). Jadi pertumbuhan satu beralih ke pertumbuhan dua, lalu tiga, dll. Secara umum, semua kolom tersebut dimulai dengan$$2 i , di mana i adalah indeks kolom. Di bawah$2^i$$$2 i nilainya tidak berubah, tetapi di atasnya berubah sesuai dengan rumus$2^i$$$2 i / j , di mana j adalah kenaikan ketika menggeser baris ke atas (lebih besar dari nol). Yaitu, sementara nomor baris ada di antara$2^i/j$$$$2^i/j$ dan $$2 i / ( j + 1 ) , kenaikan adalah sama dengan j. Setelah melewati perbatasan$2^i/(j+1)$$$2 i / ( j + 1 ) , kenaikan akan sama dengan$2^i/(j+1)$$$j + 1 , maka batas kehendak$j+1$$$2 i / ( j + 2 ) , setelah itu kenaikannya akan$2^i/(j+2)$$$$j+2$ dll. , 10 ( ), , , 2 .

, , , , 11, 13, 17. , . - , !

Pemilik bola kristal cenderung memprediksi masa depan, tetapi kita juga bisa memprediksi sesuatu dari tabel kita. Anda mungkin sudah memperhatikan - kolom bahkan unit terakhir hanya ditemukan dalam bilangan prima. Artinya, satu pandangan sekilas ke meja sudah cukup untuk memahami apakah suatu angka adalah bilangan prima atau bukan. Ini adalah prediksi pertama untuk bola kristal kami. Prediksi kedua adalah periode pecahan dalam sistem angka$$k ∗ N - 1 (di sini k adalah bilangan bulat lebih besar dari nol) selalu 2. Periode fraksi dalam sistem bilangan$k*N-1$$$k ∗ N + 1 selalu sama dengan 1 dan semua nilai di dalamnya juga sama dengan 1. Misalnya, untuk angka yang dipelajari N = 11 dengan k = 1, kita memiliki$k*N+1$$$$k*N-1=10$ , $$$1/11=0.(09)$ , 2, .

. , , $$$b^i \pmod N$ , b — , i — , , N — . , , . $$$a^{(p-1)} \pmod p = 1$ , , — $$$a^{(p-1)/2} \pmod p = \{1,p-1\}$ , , , 2, , p-1, p — . , , . Lalu $$ak(modp ) = p - ( a ( p - 1 ) / 2 + k( modp ) ) , di mana k adalah bilangan bulat apa pun, p adalah bilangan prima. Rumus ini mencerminkan keteraturan pengulangan bagian kedua dari periode genap, tetapi dengan pengurangan dari jumlah yang diteliti, ketergantungan ini digambarkan sedikit lebih tinggi. Untuk jumlah periode genap yang genap, orang dapat juga menyatakan dengan rumus ketergantungan residu dari setengah kanan periode pada residu dari separuh kiri. Sekarang kami akan memprediksi bagaimana menemukan semua pembagi angka dari tabel seperti itu. Untuk melakukan ini, lihat kembali pada tabel untuk nomor 21:$a^k \pmod p = p - (a^{(p-1)/2+k} \pmod p)$




, , . 1, ( , ), 21 . . ? , 2 1. , , , , , , , , , . , , , . , , . , .

21. , . , . 3 , №3 . №7 ( , ). . , , . . , . , — . , . . (, , N), , , . N, , .

, , , , , . 21, 3, — 7, 3. , , , . , 21 , 7, 7 . 21 7, . - , 7, 21, , , , .



Selain itu, perhatikan baris nol dengan garis No. 7 dan No. 14. Mereka dengan jelas memberi tahu kami tentang pembagian nomor 21, karena kami mengalikan hasil membagi 1/21 dengan 3, yang dikurangi dan memberikan hasilnya 1/7, tetapi baris nomor 7 dalam kasus ini menunjukkan hasil pembagian 7/7, di mana semua sisanya adalah 0. Baris nomor 14 adalah hasil dari divisi 14/7, dan di sana sisanya sama dengan nol.

, 3 №7 14 , 7, , , , 21. , , , , , 3, №7 14, . , . 21 3 7, , 3 7 . , 3, , 3. , №7 14, , , . , 3 7 14. . 7 14? — 3 , 3. , . , , ( ) . . ? .

Mengapa saya bisa menggunakan tabel yang dijelaskan? Sebagai contoh, mereka memberi kita kesempatan untuk menghasilkan urutan pseudo-acak. Dan urutan ini memiliki sejumlah properti yang bermanfaat. Jadi di setiap urutan residu tidak ada pengulangan. Jika kita membutuhkan pengulangan (untuk peniruan acak yang lebih lengkap), maka kita memiliki nilai-nilai dari periode fraksi, yang sering dapat diulang. Distribusi residu dari rangkaian sekuens lengkap untuk bilangan prima selalu seragam sempurna. Nilai sejumlah residu secara otomatis disimpan dalam kisaran [1, N-1]. Untuk mendapatkan urutan, kami memiliki jumlah bilangan prima tak terbatas, yang membuat jumlah urutan tak terbatas. Panjang urutan maksimum tidak melebihi nilai bilangan prima, yang memberikan cara sederhana untuk memprediksi parameter penting ini.Kehadiran beberapa urutan, dengan periode yang lebih pendek dari N, menjamin kami bahwa tidak ada persimpangan urutan selama generasi paralel mereka, yaitu, memuat semua inti prosesor, kami tidak perlu memikirkan kunci, sinkronisasi, pemeriksaan entri dan sejenisnya, yang sangat meningkatkan kecepatan pembuatan paralel. Selain itu, algoritma pembangkitan (pembagian demi sudut) tersedia untuk siswa sekolah dasar, dan juga sangat mudah untuk diimplementasikan secara programatik.Selain itu, algoritma pembangkitan (pembagian demi sudut) tersedia untuk siswa sekolah dasar, dan juga sangat mudah untuk diimplementasikan secara programatik.Selain itu, algoritma pembangkitan (pembagian demi sudut) tersedia untuk siswa sekolah dasar, dan juga sangat mudah untuk diterapkan secara programatis.

. , - , ( - ). - , . - ( , , , ), 10^18 . , ( — ) , - ( , - ). . ( ).

Dalam seri berikutnya, kita akan berbicara tentang teori keterbagian, dan tentang hadiah yang menunggu pembaca yang tertarik.