Dalam seri sebelumnya, kami melihat bilangan pecahan dari beberapa sudut yang tidak biasa. Dalam seri ini, setelah
pendahuluan dan beberapa
landasan teori , kami akan mencoba untuk mengumpulkan semuanya dalam bentuk yang nyaman dan mendapat manfaat dari informasi yang tersedia.
Cari yang sederhana
Setelah berbicara tentang sifat-sifat tabel residual, kita dapat mencoba menerapkan pengetahuan tentang hal itu ke penghasilan. Jadi, banyak orang di dunia merasa berguna untuk mencari bilangan prima besar. Dan bahkan ada organisasi yang siap memberikan banyak uang kepada seseorang yang menemukan bilangan prima yang besar. Tetapi topik komputasi kuantum juga populer di dunia. Mengapa Karena menjanjikan untuk meretas cryptosystem yang terkenal. Jadi, bisa dikatakan, ini adalah slogan iklan komputasi kuantum, yang memungkinkan meyakinkan setiap manajer pembuat keputusan untuk mengalokasikan uang untuk pelajaran yang begitu menarik. Karena itu, kami juga akan membicarakan topik ini.
Pertama, kami akan menunjukkan cara mencari nomor utama. Masalah utama di sini adalah kuantitas. Untuk jumlah besar, tidak ada algoritma yang memungkinkan Anda untuk dengan cepat memeriksa apakah bilangan prima ada di depan kami atau bilangan majemuk. Oleh karena itu, waktu henti maksimum untuk hari ini adalah kurang dari 25 juta tempat desimal. Ini hanya 10 megabita, pada jajaran prosesor modern ini menunjukkan waktu pemrosesan milidetik, tetapi untuk memeriksa apakah bilangan prima ada di jajaran kami, prosesor modern akan mengonsumsi listrik dan berdengung dengan kipas selama beberapa dekade. Artinya, secara teknis, ukuran prosesor tidak baik, tetapi jumlah operasi dalam algoritma yang dikenal untuk jumlah besar seperti itu sangat besar. Kenapa situasi ini?
Untuk tes kesederhanaan, misalnya, penghitungan pembagi digunakan. Tetapi berapa banyak pembagi yang Anda butuhkan untuk mengulangi selama sepuluh megabyte panjang? Jawabannya adalah bahwa bahkan atom dengan elektron di seluruh alam semesta akan cukup hanya untuk sebagian kecil dari nilai ini. Artinya, kita membutuhkan banyak alam semesta, hanya untuk menempatkan semua pembagi ini di sana. Terlalu banyak? Oleh karena itu, penghitungan pembagi untuk angka sepuluh megabyte diterapkan sampai batas tertentu (ya, alam semesta mengecewakan kita ...), tetapi untungnya ada algoritma lain. Kita dapat membedakan algoritma yang tidak menggunakan enumerasi pembagi, dan pada saat yang sama mereka dijamin untuk memberikan jawaban - sederhana di depan kita atau gabungan. Tetapi ini adalah algoritma yang sangat lambat. Artinya, mereka, tentu saja, mampu menggiling angka seratus atau dua ratus bit dengan cara itu, tetapi sepuluh megabyte bagi mereka adalah kematian sekaligus. Karena itu, Anda harus keluar dari cara yang sulit.
Tetapi masalah dengan semua triknya adalah bahwa mereka belum menghasilkan teori keterbelahan yang lengkap. Lagi pula, jika sudah lengkap, kami akan segera menemukan jawabannya - prima atau tidak. Lebih tepatnya, sebuah teori akan dengan cepat memberi kita algoritma untuk pengujian yang tidak akan membuat kita menunggu sampai kematian termal alam semesta. Itu sebabnya mereka memberikan bonus kepada mereka yang datang dengan algoritma secepat mungkin, dan, yang paling penting, seluruh teori untuk menyediakan algoritma untuk semua kesempatan.
Sementara itu, kami memiliki uji Luc-Lemer khusus, yang menggunakan koneksi nomor Mersenne yang sangat spesifik dengan urutan tertentu, tetapi tidak sisa pembagian, seperti yang baru-baru ini kami amati, tetapi jumlah derajat beberapa angka irasional. Artinya, tes kesederhanaan dibuat dari samping, katakanlah, tidak cukup jelas, meskipun beberapa di sini dapat mengambil perbandingan yang lebih rumit. Tetapi mengapa derajat bilangan irasional ternyata lebih dekat dengan tes kesederhanaan daripada semua pencapaian lain dari teori bilangan? Ternyata karena matematika tidak tahu solusi sederhana. Dan sebagai hasilnya, sebuah metode digunakan, meskipun tidak jelas tetapi masih berfungsi, dari wilayah yang tidak terdekat dengan perhitungan bilangan bulat, kira-kira bagaimana transisi dari Cartesian ke koordinat polar membantu menggunakan metode tambahan yang sangat sulit untuk diterapkan dalam koordinat Cartesian.
Selain tes Luc-Lemer, ada juga tes probabilistik. Mereka membantu menghilangkan nomor majemuk yang dijamin. Jadi salah satu tes probabilistik yang digunakan secara aktif adalah tes berdasarkan rumus Fermat, yang baru-baru ini kita bicarakan. Bagaimana cara kerjanya? Sangat sederhana - ingat kolom unit di sebelah kanan di tabel sisanya? Ini adalah tanda kesederhanaan angka yang dijamin. Untuk menjelaskan verifikasi menggunakan rumus Fermat, matematikawan menggunakan terminologi khusus yang sedikit orang mengerti selain mereka, jadi kami tidak akan pergi ke hutan matematika ini, tetapi menjelaskan semuanya dengan jari, atau lebih tepatnya, dari tabel residual. Untuk memahami apa yang tersisa di kolom terakhir, Anda harus membaginya dengan kolom dan mencapai sisanya di posisi yang mengandung 1, atau menghitung sisa ini menggunakan rumus yang memungkinkan Anda untuk mendapatkan sisanya dengan nomor posisi dan dasar sistem angka. Opsi pertama untuk angka sepuluh megabyte panjang akan membutuhkan waktu yang hampir tak terbatas, karena lebar tabel adalah N-1, yang berarti bahwa untuk sejumlah urutan satu juta, tabel akan memiliki setidaknya satu juta kolom. Untuk satu miliar, satu miliar. Untuk satu triliun, satu triliun. Tapi satu triliun, itu hanya 12 tempat desimal. Dan kami tertarik pada angka di mana di bawah 25 juta karakter. Bahkan satu triliun residu dengan metode membagi kolom, kita harus menghitung hampir kurang dari setengah jam, dan ini hanya 12 tempat desimal. Total! Dibandingkan dengan 25 juta. Apakah Anda pikir Anda punya cukup waktu untuk menunggu hasilnya dengan cara ini? Itu sebabnya lebih baik segera menghitung nilai yang diinginkan menggunakan rumus. Dan hanya rumus Fermat sesuai dengan rumus untuk menghitung sisanya di posisi terakhir dalam tabel. Selain itu, jika periode lebih pendek dari lebar tabel, maka matematika belum tahu bagaimana menghitungnya, yang berarti bahwa dalam hal apa pun, kita perlu memilih kolom terakhir. Matematikawan dalam tes cukup memeriksa apakah sisa pada kolom terakhir sama dengan satu untuk sistem bilangan yang telah mereka pilih (meskipun matematikawan tidak menggunakan konsep sistem bilangan, bagi mereka hanya ada dasar yang dinaikkan menjadi daya). Jika sisanya tidak sama dengan satu, jumlahnya dijamin komposit. Seperti yang kita lihat pada contoh tabel untuk angka 21, tidak adanya unit di akhir banyak baris yang membedakannya dari tabel untuk bilangan prima. Tapi ada satu masalah. Pada beberapa baris, mungkin masih ada unit, yang juga bisa kita verifikasi dengan contoh tabel untuk 21. Itu sebabnya matematikawan menyebut tes berdasarkan rumus probabilistik Fermat. Artinya, mereka tidak tahu apakah bilangan prima jika tes Fermat menemukan sisa sama dengan satu, karena unit palsu tersebut ada di tabel untuk angka 21, dan di banyak tabel lainnya, bahkan untuk angka sepuluh megabyte. Jadi, Anda perlu memeriksa semua garis dalam satu baris, yang merupakan waktu yang sangat lama, karena garis untuk angka sepuluh megabyte, seperti yang disebutkan sebelumnya, jauh lebih dari semua yang ada di alam semesta yang kita tahu, atau katakan saja - kemungkinan angka ini adalah prima. Inilah metode terakhir dan matematikawan telah memilih. Untungnya, ada beberapa garis yang diakhiri dengan satu di sebagian besar angka komposit. Benar, ada juga yang disebut bilangan Carmichael, di mana semua baris, kecuali kelipatan pembagi nomor tersebut, diakhiri dengan satu. Jadi, pada bilangan Carmichael, uji probabilistik dengan rumus Fermat hampir dijamin salah, karena untuk menghilangkan kesalahan Anda perlu masuk ke beberapa pembagi angka, dan sepuluh megabyte pembagi hanya dapat memiliki dua, dan nilainya bisa sangat besar, dan oleh karena itu kemungkinannya sangat besar. itu adalah sedemikian rupa sehingga, dengan pilihan acak dari basis sistem bilangan, praktis nol. Tetapi di sisi lain, angka Carmichael relatif kecil, yang memungkinkan kita untuk berharap untuk ujian probabilistik. Hanya ketika mencari bilangan prima, harapan probabilitas dikecualikan. Itulah sebabnya, setelah memilih kandidat yang sederhana dengan bantuan tes probabilitas, uji Luc-Lemer tetap diterapkan.
Tambahkan sedikit tentang nomor Carmichael. Mereka luar biasa tidak hanya karena kemampuan mereka untuk meniru yang sederhana. Jadi, jaringan memiliki situs web tempat Anda dapat mempelajari
urutan angka yang berbeda. Jika Anda memasukkan nomor 561 (angka Carmichael minimum) di bidang pencarian, Anda dapat menemukan bahwa nomor itu berpartisipasi dalam jumlah urutan yang sangat besar. Apa yang sedang dibicarakan ini? Rupanya tentang beberapa sifat struktural yang belum diketahui dari angka yang sama yang sangat umum di dunia kita. Fakta yang sangat menghibur.
Namun kembali ke tes kesederhanaan. Meskipun koefisien penyaringan yang baik dengan tes probabilitas, umat manusia menghabiskan waktu bertahun-tahun untuk menemukan bilangan prima maksimum berikutnya. Mengapa Karena ketergantungan waktu eksekusi tes pada ukuran angka adalah kuadratik. Yaitu, untuk angka-angka kecil semuanya berbunyi dengan keras dan tidak ada masalah, tetapi ketika jumlahnya meningkat satu juta kali, waktu untuk perhitungan meningkat satu triliun kali. Oleh karena itu, pada inti prosesor tunggal, kami akan mempertimbangkan tes Luc-Lemer selama beberapa dekade. Tetapi bahkan tes dengan formula Fermat, kami juga akan mempertimbangkan hal yang sama. Artinya, dalam kedua pendekatan, jumlah perhitungan telah mencapai batas kemampuan manusia. Anda harus melakukan sesuatu dengan ini, bukan?
Apa yang bisa menjadi alternatif untuk limbah komputasi yang sia-sia pada pemanas udara selama bertahun-tahun? Sangat sederhana - Anda perlu memprediksi kesederhanaan berdasarkan sifat nomornya, dengan keanggotaannya di kelas tertentu. Jadi, angka-angka Mersenne menjadi pemimpin dalam ukuran pencapaian bilangan prima yang terbukti justru karena milik mereka pada kelas tertentu. Tes Luke-Lemer bekerja khusus untuk kelas yang spesifik. Jumlah kelas lain tertinggal karena kurangnya bahkan tes yang mahal seperti tes Luc-Lemer untuk angka sepuluh megabyte (meskipun untuk beberapa, tes ini disesuaikan). Jadi kita memerlukan klasifikasi angka yang memungkinkan kita menemukan tes kesederhanaan yang sederhana, jadi surga memaafkanku untuk permainan kata-kata semacam itu.
Bagaimana cara membuat klasifikasi seperti itu? Ini juga tidak begitu sulit - Anda perlu mempelajari nomor yang berbeda dan mengidentifikasi fitur umum di antara mereka. Secara umum, inilah tepatnya yang ingin dilakukan oleh ahli matematika, tetapi sejauh ini bunga batu belum keluar. Karena itu, kami akan mencoba membantu mereka.
Pendekatan yang diuraikan sebelumnya untuk menganalisis angka-angka berdasarkan tabel residual pada dasarnya mengeksplorasi pembagian angka dalam bentuk 1000 ... 000. Yaitu, nol di sebelah kanan secara konstan ditugaskan ke unit, sehingga mengalikannya dengan basis masing-masing sistem angka yang ada dalam tabel sisa. Sebagai hasil dari analisis, kami menemukan bahwa angka yang berbeda membagi angka dari bentuk 1000 ... 000 dengan cara yang berbeda. Jadi bilangan prima umumnya tidak dapat membaginya dengan nol. Tetapi komponen, dan bahkan, misalnya, dua-dua dan / atau lima, benar-benar dibagi. Di bawah ini adalah tabel untuk nomor 8:

Seperti yang Anda lihat, di dalamnya, dalam garis yang merupakan kelipatan dari 2, setelah beberapa entri dari residu bukan nol, hanya satu nol yang tersisa. Ini persis bagaimana semua angka yang terkait dengan kelas pembagi unit dengan tampilan nol, dan keberadaan nol memberitahu kita di mana sistem angka kita akan berhasil. Tapi inilah masalahnya - dari sudut pandang menemukan bilangan prima, unit dengan nol sama sekali tidak menarik bagi kita, karena dijamin akan dibagi dengan basis sistem bilangan, yang memberi kita semua nol ini setelah satu. Jadi, Anda perlu mempelajari pembagian kelas angka lainnya. Apakah ini logis? Inilah yang akan kita lakukan.
Bisakah kita mencoba teori pembagian?
Sebelumnya kami berkenalan dengan keteraturan tabel residual untuk operasi divisi yang relatif akrab bagi kami. Pola ternyata menghibur, tetapi mereka masih memiliki masalah yang sama - mereka tidak memberi kami algoritma cepat untuk memeriksa kesederhanaan. Untuk tes seperti itu, kami, seperti dalam tes sesuai dengan rumus Fermat, harus menaikkan angka ke tingkat yang sangat besar, dan kemudian menemukan sisa pembagian hasil dengan jumlah yang diteliti. Atau hanya mengulangi semua sisa menggunakan metode "sudut" (sebelum kematian termal alam semesta, tentu saja). Berikut adalah data - operasi meningkatkan daya dengan menemukan sisanya membutuhkan waktu 15 menit pada satu inti untuk jumlah pesanan
. Dengan peningkatan ukuran angka sebanyak 1000 kali, kita mendapatkan peningkatan kuadratik (ditambah logaritma, tetapi ini tidak terlalu banyak) setidaknya 1.000.000 kali, tetapi dalam kenyataannya - banyak juta kali. Misalkan, sebagai hasilnya, kita mendapatkan sejuta jam untuk satu tes. Ini kira-kira 40.000 hari atau terasa lebih dari seratus tahun. Jika kami mengoptimalkan pelaksanaan pengujian hingga ke tingkat yang sebenarnya, lakukan dengan mempertimbangkan semua fitur arsitektur prosesor, maka mungkin alih-alih seratus tahun kami mendapatkan 10. Pada 10 core - 1 tahun. Untuk 1000 core - 4 hari. Tapi ini hanya tes probabilistik, karena ada yang menyamar sebagai angka komposit sederhana. Jadi, Anda masih perlu memeriksa ulang. Tetapi yang lebih penting adalah kenyataan bahwa jumlah kandidat adalah jutaan. Setelah semua kemungkinan penyaringan, akan ada banyak penyaringan. Karena itu, dunia masih mengotak-atik angka sepuluh megabyte.
Tapi kami punya alat. Tabel sisanya juga berfungsi untuk jenis angka lainnya. Misalnya, ambil nomor Mersenne. Dalam biner, itu hanya urutan unit. Apa yang mencegah kita menjelajahi urutan unit alih-alih urutan nol? Ya, tidak ada yang mencegah. Dan ternyata untuk urutan seperti itu, metode kami bekerja cukup baik dan sejumlah pola yang diidentifikasi sebelumnya dipertahankan di dalamnya. Ini adalah hasil untuk angka 7:

Seperti yang dapat kita lihat, bilangan prima 7 di semua sistem bilangan (kecuali kelipatan tujuh) adalah pembagi bilangan Mersenne. Artinya, hampir setiap baris mengandung nol yang memberi tahu kita tentang pembagian angka dari bentuk 111 ... 111 (dalam sistem biner) oleh 7. Jadi, ketika bekerja dengan sistem angka biner, kita melihat bahwa angka 7 membagi semua angka Mersenne, panjangnya yang merupakan kelipatan dari 3. Hasil ini jelas tanpa tabel residu - angka 7 dalam bentuk biner terdiri dari tiga unit (111), sehingga akan membagi angka biner dari tiga unit. Dan jika ada lebih banyak unit, maka pembagiannya terlihat seperti ini:
111111 | 111 ------ 111 1001 111 111 111
Artinya, kita cukup meletakkan tujuh (dalam bentuk biner) di bawah dividen. Dan berapa kali ketujuh cocok - begitu banyak tiga unit dalam jumlah yang dapat dibagi. Jika di dalamnya jumlah unit bukan kelipatan tiga, maka jumlah tersebut tidak dapat dibagi dengan 7. Tapi ini semua jelas hanya selama kita mempelajari angka dengan struktur yang identik (7 dan 63, seperti pada contoh). Dan jika struktur angka lebih rumit, tabel residu akan membantu kita. Jadi, untuk semua sederhana kami mendapatkan hasil yang serupa, tetapi dengan periode pembagian yang sedikit lebih lama. Di bawah ini adalah contoh angka 11 (angka tersebut sudah dalam desimal):
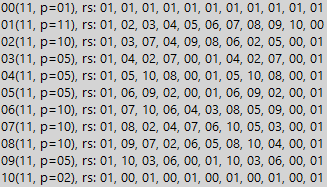
Kita melihat bahwa dalam sistem biner, jarak ke nol (periode pembagian) untuk angka 11 adalah 10. Artinya, setiap angka Mersenne yang mengandung 10k unit, di mana k adalah bilangan bulat lebih besar dari nol, harus dapat dibagi dengan 11. Dapat dengan mudah dibuktikan bahwa sisanya sederhana. angka berperilaku sama persis, kecuali untuk ukuran periode, tentu saja. Tetapi untuk kompleks, situasinya kembali kurang harmonis. Di bawah ini kita melihat contoh untuk nomor 8:

Rupanya, 8 tidak bisa membagi angka Mersenne dalam bentuk biner. Di sini, di ternary - tolong, tetapi angka Mersenne hanya terdiri dari unit dalam bentuk biner. Situasinya mirip dengan bilangan majemuk lainnya - mereka memiliki segalanya dengan cara yang berbeda. Gambar ramping dan simetris untuk bilangan prima tidak berulang untuk gambar majemuk. Tetapi bagi kita justru yang sederhana yang penting, karena jika jumlahnya dibagi menjadi prima, maka sama sekali tidak ada masalah jika itu juga akan dibagi menjadi senyawa yang termasuk sederhana ini. Tetapi jika jumlahnya tidak dibagi menjadi yang sederhana, maka tidak mungkin untuk dibagi menjadi senyawa dengan yang sederhana. Jadi, kita harus tertarik hanya pada bilangan prima.
Sekarang mari kita rangkum. Kita tahu bahwa angka-angka Mersenne dibagi menjadi bilangan prima dan bahwa untuk dapat dibagi, angka-angka Mersenne memerlukan sejumlah unit yang merupakan kelipatan dari periode pembagian dari angka yang diteliti. Tetapi kita juga tahu bahwa kandidat untuk bilangan prima Mersenne hanya mereka yang jumlah unitnya juga bilangan prima. Artinya, jumlah ini tidak dibagi menjadi apa pun kecuali satu unit dan itu sendiri. Oleh karena itu kesimpulannya - kita membutuhkan bilangan prima seperti itu yang periode pembagiannya sama dengan panjang angka Mersenne. Jika untuk beberapa panjang nomor Mersenne kami tidak menemukan pembagi dengan periode yang sesuai, kami memiliki sebelum kami nomor Mersenne utama. Tampaknya sederhana.
Tetapi kesulitan lebih lanjut dimulai. Bagaimana menemukan nomor yang periodenya bertepatan dengan panjang nomor Mersenne? Untuk menjawab pertanyaan ini, Anda harus menyelesaikan tugas sederhana - untuk menemukan cara dengan cara sederhana untuk mengetahui periode untuk bilangan prima acak. Untuk saat ini, kami hanya dapat berbagi sudut atau menyodok di tempat tertentu menggunakan rumus dengan derajat besar. Tetapi jika kita dapat menghitung periode tanpa perlu perhitungan panjang, kita akan segera menemukan pembagi yang tepat, atau kita akan memastikan bahwa tidak ada yang alami. Persis tugas sederhana yang sama menanti kita dalam hal mempelajari pembagian angka dari bentuk 1000 ... 000. Jadi periode keterbelahan sangat penting dalam semua hal.
Bagaimana cara mencari titik?
Di sini, komputer kuantum bergegas membantu kami. Sekali waktu, pada suatu waktu dahulu kala, seorang ahli fisika kuantum tertentu dengan nama Shor, menyarankan menemukan periode tepat dengan bantuan komputer kuantum. Bahkan, komputer kuantum hanya memberikan nilai menengah, dari mana komputer biasa kemudian menerima periode, tetapi intinya bukan itu, tetapi tanpa komputer kuantum, matematika tidak dapat menghitung periode. Tetapi menghitung periode, kita mendapatkan kesempatan untuk secara akurat menghitung nilai sisanya secara ketat di tengah periode. Mengapa ini dibutuhkan? Untuk fakta bahwa dari itu Anda bisa mendapatkan faktor-faktor yang tentu saja mengandung nilai tertentu yang merupakan kelipatan dari pembagi angka yang diteliti. Ini dilakukan dengan menambah sisa unit dan mengurangi unit. Dua angka yang dihasilkan dapat dilewati melalui algoritma cepat untuk menemukan pembagi umum terbesar dengan nomor yang diteliti. Setidaknya dalam satu kasus, kita mendapatkan pembagi nomor yang diselidiki. Benar, tidak semuanya begitu sempurna, karena seperti yang kita lihat pada contoh tabel untuk bilangan prima, di tengah-tengah barisan sering ada tambahan untuk nomor yang diselidiki (N-1), dalam formulir ini kita dapatkan:
Oleh karena itu dalam satu kasus kami memiliki nomor yang dipelajari sendiri, dan tidak masuk akal untuk menghitung faktor umum terbesar, dan dalam kasus kedua, kami telah menjamin bahwa itu tidak memiliki pembagi umum dengan nomor yang dipelajari. Tidak ada pembagi umum karena angka ini hanya 2 kurang dari jumlah yang diselidiki, yang berarti bahwa tidak peduli berapa pun jumlah yang cocok dengan jumlah bilangan bulat yang dipelajari (akan menjadi pembagi nya), dengan mengurangkannya dari angka yang diteliti, kami mendapatkan jaminan lebih rendah nilai dari
, atau menggunakan rumus:
N-x <N-2 \ Rightarrow x> 2 \; \ & \; (N-2) / x \ ne m
Di sini N adalah angka tes ganjil (ganjil karena kelipatan dua dapat dibagi dua, dan kita tidak perlu membagi dengan apa pun), x adalah pembagi N, k adalah seluruh hasil pembagian
, m adalah seluruh hasil pembagian
. Artinya, kita kadang-kadang harus mengubah sistem angka dan meminta komputer kuantum untuk menemukan periode baru, dengan harapan bahwa di tengah akan ada nomor yang lebih cocok. Batasan plus adalah paritas wajib dari nilai panjang periode. Tetapi semua ini tidak begitu menakutkan, karena bagaimanapun, komputer kuantum akan menghitung panjang (atau beberapa panjang) yang kita butuhkan jauh lebih cepat daripada kematian termal alam semesta terjadi, tidak seperti algoritma lainnya.
Meskipun menghitung periode untuk memperoleh pembagi angka adalah tugas yang sedikit berbeda dari menemukan yang sederhana. Namun demikian, kita dapat menambahkan sesuatu di sini menggunakan tabel sisa. Jadi, tabel menunjukkan bahwa tengah baris dengan panjang genap biasanya adalah angka yang memenuhi kondisi berikut:
Di sini r adalah sisa yang diinginkan, dan N adalah nomor yang sedang diselidiki. Jadi, ternyata tidak perlu mencari periode untuk mendapatkan pembagi angka, karena suatu periode dicari untuk menemukan sisa r, dan kemudian menambah dan mengurangi satu dari itu. Artinya, Anda dapat segera menemukan sisa ini yang memenuhi kondisi di atas. Benar, pencarian untuk nilai seperti itu juga nontrivial. Tapi mungkin komputer kuantum bisa dipenjara karena hal seperti itu? Para ahli dalam komputasi kuantum perlu memahami berapa qubit yang dibutuhkan untuk ini (qubit adalah parrot yang mengukur "kekuatan" komputer kuantum). Meskipun, mungkin, Anda bisa melakukannya tanpa komputer kuantum. Untuk melakukan ini, Anda hanya perlu memahami pola apa yang akan berguna. Beberapa pola terlihat dalam tabel residual, tetapi sisa pembaca harus mencari tahu sendiri, dan kemudian Anda pasti akan memecahkan kriptografi berbasis RSA. Benar, ada beberapa kesulitan - pertama Anda perlu menemukan pola yang bermanfaat ini, yah, dan kemudian ... Maka mereka mungkin tidak membayar Anda uang. Pertama, hadiah diberikan untuk bilangan prima besar, bukan untuk peretasan RSA. Dan kedua - yah, pikirkan sendiri berapa banyak organisasi serius di dunia yang tertarik untuk mencegat data orang lain dengan cara ini? Dan beberapa FSB (CIA, Mossad, Mi-5, hanya Mafia) mengetahui bahwa Anda tahu sesuatu. Coba tebak apa yang akan terjadi padamu? Karena itu, lebih jauh Anda hanya bertindak atas risiko dan risiko Anda sendiri.
Benar, topik kuantum itu sendiri cukup menarik karena mengandung ketidakpastian kuantum, fluktuasi vakum, dan Darwinisme kuantum lainnya. Bagaimana semua ini bisa dijelaskan? Sejujurnya, saya tidak tahu, tapi saya melihat analogi dengan tabel sisanya. Misalnya, ketika seseorang mengamati nilai-nilai dalam tabel residual dan tidak tahu tentang pola yang disebutkan sebelumnya, maka baginya hanya ada beberapa kebisingan di tabel di mana angka-angka berubah satu sama lain secara acak, seperti beberapa fluktuasi dalam ruang hampa. Tetapi jika Anda memahami bahwa kami hanya menerapkan algoritme yang sama untuk pasangan "urutan - angka yang sedang diselidiki" yang berbeda, maka semua bubur mendidih dari angka-angka ini langsung dapat dipahami. Dan dengan cara yang sama, menjadi jelas mengapa, di antara sekumpulan besar nilai yang mungkin untuk mengisi tabel, hanya yang didefinisikan secara ketat yang benar-benar tetap berada di dalamnya. Tetapi sampai kita mendapatkan "interaksi" dari urutan dengan angka yang dipelajari, kita tidak dapat memprediksi isi tabel. Lebih tepatnya, setiap isian itu akan sama-sama memungkinkan. Tetapi setelah "interaksi" - semuanya akan menjadi sangat logis, dari kemungkinan yang sama probabilitas tunggal akan dilahirkan hanya untuk satu opsi. Dan bukan karena Darwinisme tertentu berfungsi, tetapi hanya karena penerapan algoritma tertentu untuk input data tertentu. Jika Anda tidak tahu tentang algoritme, maka mungkin tampak bahwa baris dalam tabel memang bergaya Darwin. Dan jika Anda tahu - semuanya sangat sederhana. Mungkin dalam fisika kuantum perlu untuk mencari tidak hanya partikel, tetapi juga algoritma untuk "pembagian" mereka?
Dan lagi tentang periode
Namun, masa itu sangat penting bagi kami. Ya, ini adalah bagaimana mereka akan menjawab Anda di hot line tentang masalah matematika yang membara. Seperti ditunjukkan di atas, pengetahuan tentang periode memungkinkan untuk memahami apakah angka memiliki pembagi, atau dengan cara lain apakah itu prima. Karena itu, kami melanjutkan tentang periode tersebut. Sejauh ini, kami tahu sejumlah properti periode (keunikan nilai, simetri dengan panjang genap, dll.), Tetapi kami tidak tahu cara menentukan panjangnya. Meskipun ada batas atas dan bawah - periode tidak boleh lebih lama dari jumlah yang diselidiki minus satu, dan juga periode tidak boleh lebih pendek dari periode pertumbuhan basis sistem angka sampai jumlah yang diteliti melebihi (untuk tujuh itu adalah 3, untuk 11 itu adalah 4, dll. .). Anda dapat mencoba menerapkan undang-undang yang diketahui dari tabel yang dipelajari dan mendapatkan yang baru, tetapi sejauh ini ada beberapa arahan di sini, yang sebagian besar tidak mengarah pada kesuksesan, meskipun sampai Anda mencoba masing-masing, Anda tidak akan tahu.
Karena itu, cara yang paling menjanjikan adalah menciptakan teori keterbagian yang lebih baik. Berdasarkan urutan karakteristik residu, dimungkinkan untuk mengungkapkan undang-undang pembagian banyak kelas kelas. Sejauh ini, hanya dua kelas yang telah ditunjukkan (angka dan angka Mersenne sama dengan derajat sistem bilangan), tetapi pada kenyataannya ada jumlah tak terbatas dari mereka. Bagaimana mengolah pengetahuan tentang semua kelas angka? Hanya dalam pekerjaan paralel yang masif, dan bukan dalam bentuk pemanas udara besi, tetapi dalam bentuk orang-orang yang bekerja bersama dalam tugas sebesar itu. Hasil yang ideal adalah terciptanya teori umum tentang keterbagian semua kelas angka. Ini untuk permulaan, dan kemudian pembagian polinomial dan aljabar lainnya akan hilang. Tetapi haruskah kita mengharapkan massa pikiran manusia yang sedemikian menakjubkan atas tugas menemukan bilangan prima? Saya kira tidak. Karenanya, sayangnya, kita kembali membutuhkan cara lain.
Secara teoritis, ada cara seperti itu
Jika kita mempelajari urutan terbagi alternatif, termasuk nilai yang berbeda, kami menemukan bahwa periode pembagian urutan tersebut tumbuh kelipatan dari panjang fragmen berulang dari urutan. Di bawah ini adalah contoh urutan 1010 ... 1010, di mana nol dan satu berubah secara berkala. Urutan yang diberikan selalu dibagi ke dalam dasar sistem angka, tetapi dalam kasus ini, kesederhanaan contoh mempelajari angka-angka kelas periodik hanya penting bagi kami, jadi kami tidak memperhatikan pembagian dengan konstruksi.

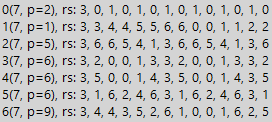
Di sini kita melihat dua tabel untuk angka 7 dan urutan yang ditunjukkan di atas, satu adalah normal, dan tabel kedua dikalikan dengan 3. Dari pola yang diidentifikasi sebelumnya dalam contoh ini, bahkan ada lebih sedikit, tetapi, bagaimanapun, untuk sistem angka pada basis 1 dan 6, kita melihat menambah panjang periode menjadi
. Dan untuk dikalikan dengan 3 tabel, kita melihat hilangnya pembagian untuk basis sistem nomor 2 dan 5, yang cukup menghibur dalam dirinya sendiri (properti keterbagian telah berubah dari multiplikasi). Tetapi lebih penting dari itu. Penting untuk memahami kemungkinan menerapkan tabel yang dapat dibagi-bagi pada urutan apa pun. Tetapi mengapa kita perlu urutan? Misalnya, untuk meningkatkan periode minimum pembagian.
Jika periode minimum dapat diperpanjang, maka ini memungkinkan kita untuk melanjutkan proses pembangunan bilangan prima. Ya, bilangan prima tidak dapat dihitung, tetapi dibangun secara matematis. Ketika periode panjang, sejumlah kecil membagi yang besar, yang berarti bahwa jika semua angka memiliki periode besar, maka untuk pembagi angka besar hanya bisa menjadi angka kecil. Apa yang diberikannya? Ini memungkinkan untuk menemukan semua pembagi angka dalam jumlah besar dengan pencarian sederhana. Karena angka kecil membagi angka besar, ukuran angka-angka kecil ini membantu komputer kita memecahkan masalah yang tidak dapat mereka pecahkan dengan pembagi besar. Oleh karena itu, arahan lebih lanjut dari pencarian bilangan prima menjadi jelas - kita perlu menemukan urutan yang memberi kita periode minimum besar. Mengapa minimum? Karena kita masih tidak tahu bagaimana menghitung periode tanpa menghitung semua residu atau menaikkan ke daya, dan karena itu kita tidak bisa hanya menemukan periode yang cukup panjang jika lebih besar dari minimum, yah, kita tahu periode minimum hanya dari analisis tabel sisa, yaitu, kita tidak perlu menghitungnya . Nah, ketika kita menemukan urutan yang kita butuhkan (dan hanya untuk ini kita dapat menggunakan analisis banyak kelas dari urutan seperti itu), kita cukup memilih panjang urutan yang tidak akan cocok dengan periode minimum yang kita ketahui. Artinya, kami akan mengambil sejumlah besar, yang jelas tidak memiliki pembagi. Dan jika ukurannya besar, hadiah menanti kita. Pada saat yang sama, kita tidak akan tertarik lebih dari periode minimum, karena mereka sudah membagi jumlah yang sangat besar, yang akan kita capai nanti.
Yang tersisa adalah menemukan urutan yang benar. Siapa yang akan mengambilnya? Tetapi bahkan jika kita tidak menemukannya, maka untuk enkripsi yang disebutkan di atas, bekerja dengan urutan alternatif akan memungkinkan untuk menambahkan istilah lain pada sandi yang meningkatkan kekuatan kriptografi - sekarang cracker sandi perlu menebak urutan yang telah kita pilih, yang dapat jumlahnya tak terbatas. Plus, untuk menghasilkan urutan pseudo-acak, kita mendapatkan pengulangan nilai dalam seri residu, dan bukan hanya dalam seri periode fraksi.
Dan akhirnya - hadiahnya!
Electronic Frontier Foundation siap membayar siapa pun pertama $ 150rb, dan kemudian $ 250rb. Total -
$ 400k . Bukankah itu mengganggumu? Lalu langsung ke intinya! Tetapi masalahnya sederhana - Anda perlu menemukan bilangan prima seratus juta tempat desimal. Ini kira-kira 300 juta bit, atau 40 megabita. Baru saja menyalip rekor saat ini 4 kali. Dan kemudian Anda membutuhkan satu miliar angka desimal panjang. Ini sudah 400 megabita. Dan semua, untuk dua angka - 400 ribu dolar hijau selamanya.
Sebenarnya, ini bukan angka yang mengerikan. Sekarang, jika kita bisa pergi dari penghitungan sisa pembagian derajat besar dengan jumlah yang diteliti ... Untuk urutan sederhana dari bentuk 100 ... 00 dan 111 ... 111, derajat itu harus ada. Tapi mungkin ada urutan di mana rumus untuk menghitung anggota ke-i dari serangkaian residu akan lebih sederhana? Atau Anda benar-benar dapat menemukan urutan dengan periode minimum yang besar. Lagi pula, periode apa yang kita butuhkan? Hanya 300 juta (dalam bentuk biner). Jika urutan tertentu memberi kita periode minimum dari bentuk 100 * N, di mana N adalah angka yang sedang diselidiki, maka hingga 3 juta angka akan cukup bagi kita untuk menemukan angka $ 150k senilai. Dan hingga 30 juta untuk angka $ 250rb. Dan sekarang, ketika periode singkat dapat terjadi dalam jumlah yang sangat besar (untuk urutan 100..00 dan 111 ... 111), kami tidak memiliki kemungkinan sederhana untuk menemukannya. Tetapi ada harapan dan itu semua tergantung pada pilihan yang berhasil dari arah pencarian. Iterasi melalui urutan satu per satu tampaknya tidak realistis untuk satu orang, tetapi Anda dapat mencoba kerumunan.
Nah, ketika Anda menemukan angka yang diperlukan, sedikit birokrasi menunggu Anda. Pertama, Anda harus menerbitkan artikel dalam jurnal matematika di AS atau Inggris atau Kanada atau Australia, dan jurnal tersebut harus dari daftar yang ditunjukkan oleh Electronic Frontier Foundation (EFF) (ini adalah jurnal yang sangat terkenal). Dalam artikel tersebut, Anda harus membuktikan bahwa metode Anda benar-benar memungkinkan untuk menemukan bilangan prima yang diinginkan. Kemudian Anda mengirim surat kebahagiaan ke EFF (di alamat tertentu), di mana Anda menunjuk ke artikel yang diterbitkan dan kemudian menunggu pesanan dari EFF. Pesanan mungkin terkait dengan memeriksa semua yang Anda lakukan untuk menemukan nomornya. Seharusnya tidak ada rahasia, atau tindakan ilegal atau meragukan. Dan itu saja, setelah itu - hadiah Anda.
Penyergapan apa yang bisa menunggu Anda di jalan? Nah, sebagai permulaan - untuk menemukan bilangan prima dan tidak membuat kesalahan saat mencarinya. Selanjutnya Anda perlu menulis dalam jurnal yang solid. Karena majalah ini padat, reaksi umum dari editor terhadap surat penemu mesin gerak abadi adalah sebagai berikut:
- Apa? Orang aneh lain? Ke keranjang!
Tetapi mungkin saja Anda memiliki pengalaman dalam menulis artikel dan Anda dapat dengan mudah mengatasi masalah ini. Dan kemudian Anda akan menemukan cek. Saya tidak tahu apa bukti Anda akan dipelajari oleh EFF, tetapi mereka menulis bahwa mereka dapat tertarik pada segalanya, apa pun. Ini akan sangat menarik jika tujuan EFF tidak sesuai dengan hasil yang Anda berikan. Jadi mereka menyatakan tujuan mengembangkan metode untuk menggunakan komputer pribadi untuk menempatkan mereka dalam penggunaan jarak jauh sementara untuk komputasi pihak ketiga.
Hadiah sebelumnya diberikan hanya untuk pembuatan dan promosi program, yang diunduh oleh sukarelawan dan dengan demikian menyediakan terraflops yang diperlukan untuk menggiling bilangan prima. Bagaimana EFF terkait dengan menghitung prime tanpa terraflops massal - saya tidak tahu. Secara teoritis, tidak ada batasan pada persyaratan mereka, sehingga kesuksesan sepenuhnya dimungkinkan.Itu saja, setelah melalui dua tahap yang ditunjukkan (dan tidak lupa untuk menemukan nomor yang diperlukan pada tahap nol), Anda menunjukkan bank dan nomor rekening di mana hadiah jatuh kepada Anda. Satu jumlah besar. Anda berurusan dengan pajak dengan biaya Anda sendiri.Alih-alih sebuah epilog
Sekali waktu, Pierre Fermat, bukan seorang ahli matematika, menemukan banyak pola untuk teori bilangan. Pria itu hanya bertanya-tanya, ada waktu luang. Dan di sini Anda memiliki prestasi yang masih diingat. Contoh lain adalah Evarist Galois. Dia mengambil matematika pada usia 16, dan pada usia 20 dia meninggal dalam duel. Selama 4 tahun ia mencoba menarik minat banyak ahli matematika dengan penemuannya, tetapi tidak berhasil. Setelah kematiannya, karyanya tetap dihargai dan bagi mereka kita berhutang penciptaan cabang matematika seperti teori kelompok, serta pengembangan aljabar. Sekali lagi - itu menarik bagi seseorang untuk menemukan bintang-bintang, tetapi mengatur karya sesuai aturan bukan untuknya. Namun untungnya, karyanya diformalkan oleh orang lain. Dan contoh lain - George Cantor, yang merefleksikan konsep himpunan yang terkenal dan elemennya, seseorang menyimpulkan teori tersebut pada akhir abad ke-19,yang hebat matematika setuju untuk menganggap layak untuk menjadi dasar ratu ilmu.Kenapa semua cerita ini? Seperti yang biasa dikatakan Obama, "Anda bisa!" Ya, slogan Amerika ini sangat cocok untuk orang-orang yang antusias. Meskipun perkembangan ilmu pengetahuan saat ini, itu tidak lengkap, itu tidak sempurna, dan ada tempat-tempat di mana kaki seorang ilmuwan sejati belum melangkah. Jadi, mari nyalakan keingintahuan kita dan mencoba mencari jalan yang tidak dijejali, dan bagaimana jika Anda berhasil?