Bukti baru memecahkan perkiraan angka seperti pi

Orang-orang Yunani kuno tertarik pada apakah mungkin untuk secara kasar mengekspresikan bilangan irasional dalam pecahan. Membuktikan hipotesis Duffin-Schaffer yang sudah lama ada , dua matematikawan memberikan jawaban yang lengkap.

Notasi biner π tidak terbatas. Tetapi jumlah fraksi yang tak terbatas dapat mendekati angka ini dengan akurasi yang semakin meningkat.

Penurunan yang dalam pada garis angka tidak dapat ditembus seperti yang terlihat. Ini adalah salah satu konsekuensi dari bukti baru yang bermakna tentang bagaimana bilangan kompleks meminjamkan diri pada perkiraan sederhana.

Buktinya memecahkan masalah hampir 80 tahun yang lalu, yang dikenal sebagai hipotesis Duffin-Shaffer. Dengan demikian, ini memberikan jawaban akhir yang telah diduduki matematikawan sejak zaman kuno: di bawah kondisi apa mungkin untuk mewakili bilangan irasional yang berlangsung sangat lama - seperti pi - dengan fraksi sederhana tipe 22/7? Bukti menyatakan bahwa jawaban untuk pertanyaan yang agak umum ini ditemukan sebagai hasil dari perhitungan tunggal.

"Ada kriteria sederhana untuk apakah Anda dapat mendekati hampir semua angka atau hampir tidak ada angka," kata James Maynard dari Universitas Oxford, penulis bersama bukti yang ia buat dengan Dimitris Cuculopoulos dari University of Montreal.

Matematikawan telah menduga selama beberapa dekade, kriteria sederhana ini adalah kunci untuk memahami kapan perkiraan yang baik dapat diperoleh - tetapi mereka tidak dapat membuktikannya. Cuculopoulos dan Maynard mampu melakukan ini hanya setelah mereka merumuskan kembali masalah angka dalam hal hubungan antara titik dan garis grafik - perubahan besar dalam perspektif.

"Saya akan mengatakan mereka cukup percaya diri (dan itu jelas dibenarkan) untuk mengambil jalan yang dipilih," kata Jeffrey Waaler dari University of Texas di Austin, yang memiliki andil dalam hasil awal terkait dengan hipotesis Duffin-Schaffer. "Kerja bagus."

Aritmatika eter

Dengan bilangan rasional, semuanya sederhana. Mereka termasuk angka untuk menghitung objek dan semua angka lain yang dapat ditulis dalam pecahan.

Karena kemampuan ini untuk dituliskan, bilangan rasional paling dikenal oleh kita. Namun, di antara semua bilangan real, yang rasional sebenarnya cukup sedikit. Sebagian besar angka-angka itu tidak rasional , dengan notasi desimal tak terbatas, dan angka-angka itu tidak dapat ditulis dalam pecahan. Beberapa dari mereka ternyata cukup penting untuk pantas notasi simbolis - pi, e, √2. Sisanya bahkan tidak bisa dipanggil. Mereka ada di mana-mana, tetapi tidak dapat dicapai - seperti eter aritmatika.

Mungkin, oleh karena itu, wajar untuk berpikir - jika kita tidak dapat secara akurat mengungkapkan bilangan irasional, seberapa dekat kita dengan mereka? Ini adalah area perkiraan rasional. Matematikawan zaman kuno menyadari bahwa rasio keliling lingkaran terhadap diameter dapat diperkirakan dengan cukup baik menggunakan fraksi 22/7. Kemudian, matematikawan menemukan pendekatan terkompresi yang lebih akurat dan hampir sama ke pi: 355/113.

"Menulis pi sangat sulit," kata Ben Green dari Oxford. "Orang-orang mencoba untuk menemukan perkiraan pi yang paling akurat, dan salah satu cara umum untuk melakukan ini adalah dengan menggunakan bilangan rasional."



Pada tahun 1837, ahli matematika Peter Gustav Lejeune dari Dirichlet menemukan aturan yang memberitahu kita seberapa akurat bilangan irasional dapat diperkirakan menggunakan bilangan rasional. Perkiraannya mudah ditemukan jika Anda tidak menetapkan nilai kesalahan yang tepat. Tetapi Dirichlet membuktikan adanya hubungan yang jelas antara pecahan, bilangan irasional, dan kesalahan yang memisahkan mereka.

Dia membuktikan bahwa untuk bilangan irasional ada banyak fraksi yang mendekatinya semakin dekat. Lebih tepatnya, kesalahan setiap fraksi tidak lebih dari 1 dibagi dengan kuadrat penyebut. Sebagai contoh, fraksi 22/7 kira-kira mengekspresikan pi dengan akurasi 1/7 ² , atau 1/49. Fraksi 355/113 tidak lebih jauh dari pi daripada pada 1/113 ² , atau 1/12 769. Dirichlet membuktikan bahwa ada banyak fraksi yang tak terhingga banyaknya, semakin dekat dan semakin dekat ke pi dengan meningkatnya penyebut.

"Suatu hal yang luar biasa dan luar biasa adalah kemampuan untuk secara kasar mengekspresikan bilangan real melalui pecahan, dengan kesalahan tidak melebihi satu dibagi dengan kuadrat penyebut," kata Andrew Granville dari University of Montreal.


Dalam naskah tahun 1913, ahli matematika Srinivasa Ramanujan Iyengor menggunakan fraksi 355/113 sebagai perkiraan pi yang rasional.

Penemuan Dirichlet adalah pernyataan terbatas tentang perkiraan rasional. Dikatakan bahwa untuk bilangan irasional Anda dapat menemukan banyak fraksi yang mendekatinya, jika Anda dapat menggunakan bilangan bulat sebagai penyebut, dan Anda puas dengan kesalahan dalam ukuran kuadrat terbaliknya. Tetapi bagaimana jika Anda membutuhkan penyebut untuk menjadi bagian dari himpunan bilangan bulat (tak terbatas), misalnya, ke himpunan bilangan prima, atau ke himpunan kuadrat penuh ? Bagaimana jika Anda ingin kesalahan aproksimasi menjadi 0,00001, atau memiliki nilai lain? Apakah Anda dapat menemukan banyak fraksi yang mendekati tak terhingga tepatnya dalam kondisi seperti itu?

Hipotesis Duffin-Shaffer adalah upaya untuk menciptakan platform paling umum untuk bekerja dengan pendekatan rasional. Pada tahun 1941, matematikawan R.D. Duffin dan A.S. Schafer mempresentasikan skenario berikut. Pertama, pilih daftar penyebut tanpa akhir. Ini bisa menjadi semua yang Anda inginkan: angka ganjil, angka dibagi 10, angka prima.

Kemudian, untuk setiap nomor dalam daftar, pilih seberapa akurat Anda perlu memperkirakan angka irasional. Intuition memberi tahu kita bahwa jika kita memilih kesalahan yang cukup besar, kita akan memiliki lebih banyak peluang untuk perkiraan. Jika Anda memilih ukuran kesalahan kecil, itu akan lebih sulit. "Urutan apa pun akan dilakukan jika cukup ruang tersisa," kata Kukulopoulos.

Sekarang, mengingat parameter yang dipilih - urutan angka dan kesalahan tertentu - muncul pertanyaan: apakah mungkin untuk menemukan jauh lebih banyak fraksi yang mendekati semua bilangan irasional?

Hipotesis menyediakan fungsi matematika untuk mengevaluasi pertanyaan ini. Parameter Anda bertindak sebagai input. Hasilnya bisa menjadi salah satu dari dua opsi. Duffin dan Schaffer menyarankan bahwa dua opsi ini sesuai persis dengan apakah urutan Anda dapat mendekati hampir semua angka irasional dengan akurasi yang diperlukan, atau hampir tidak ada dari mereka ("praktis" disebutkan karena untuk setiap rangkaian penyebut akan selalu ada sejumlah kecil bilangan irasional terisolasi yang dapat atau tidak dapat didekati dengan cukup baik).

“Kamu mendapatkan hampir semuanya atau hampir tidak ada. Tidak ada opsi perantara, ”kata Maynard.

Ini adalah pernyataan yang sangat umum, mencoba untuk mencirikan perkiraan dengan bilangan rasional di sepanjang dan di seberang. Kriteria yang diajukan oleh Duffin dan Schaffer tampak benar bagi matematikawan. Namun, untuk membuktikan bahwa keluaran biner dari fungsi tersebut berisi semua yang Anda butuhkan untuk memahami apakah perkiraan Anda berfungsi atau tidak, itu jauh lebih sulit untuk dilakukan.

Penghitungan ganda

Bukti dari hipotesis Duffin-Schaffer adalah untuk memahami manfaat apa yang Anda dapatkan dari masing-masing penyebut yang tersedia bagi Anda. Untuk merasakan ini, akan berguna untuk mempertimbangkan versi yang lebih kecil dari tugas ini.

Misalkan Anda ingin memperkirakan semua bilangan irasional pada segmen dari 0 hingga 1. Bayangkan bahwa semua bilangan asli dari 1 hingga 10 tersedia sebagai penyebut. Daftar fraksi yang mungkin cukup besar. Pertama 1/1, kemudian 1/2 dan 2/2, lalu 1/3, 2/3 dan 3/3, dan seterusnya, hingga 9/10 dan 10/10. Namun, tidak ada manfaatnya.

Misalnya, 2/10 sama dengan 1/5, dan 5/10 sama dengan 1/2, 2/4, 3/6 dan 4/8. Sebelum kemunculan hipotesis Duffin-Schaffer, ahli matematika Soviet Alexander Y. Khinchin merumuskan hipotesis tentang pendekatan rasional yang serupa dalam luasnya. Namun, teorinya tidak memperhitungkan fakta bahwa fraksi setara harus dihitung hanya satu kali.


Dimitris Cuculopoulos (kiri) dan James Maynard pada presentasi buktinya di sebuah konferensi di Italia

"Biasanya, matematika untuk kelas satu seharusnya tidak mempengaruhi pemecahan masalah," kata Granville. "Tapi dalam kasus ini, secara mengejutkan, dia mempengaruhi."

Oleh karena itu, hipotesis Duffin-Shaffer memiliki istilah yang menghitung jumlah fraksi unik (atau fraksi berkurang) untuk setiap penyebut. Anggota ini disebut fungsi φ Euler untuk menghormati penemunya, ahli matematika abad ke-18, Leonard Euler. φ (10) adalah 4, karena antara 0 dan 1 hanya ada empat pecahan tereduksi dengan penyebut 10: 1/10, 3/10, 7/10 dan 9/10.

Langkah selanjutnya adalah menghitung berapa bilangan irasional yang dapat diperkirakan menggunakan masing-masing fraksi yang diberikan. Itu tergantung pada kesalahan ukuran apa yang ingin Anda terima. Hipotesis Duffin-Shaffer memungkinkan kita untuk memilih kesalahan masing-masing penyebut. Misalnya, untuk pecahan dengan penyebut 7, Anda bisa mengambil kesalahan yang diizinkan sebesar 0,02. Untuk penyebut 10, Anda dapat mengambil kesalahan 0,01.

Setelah mengidentifikasi penyebut dan ketentuan kesalahan, sekarang saatnya untuk menempatkan jaringan pada angka yang tidak rasional. Bangun pecahan Anda pada garis bilangan antara 0 dan 1, dan gambar kesalahan dalam bentuk jaringan yang membentang dari pecahan di setiap sisi. Kita dapat mengatakan bahwa semua bilangan irasional yang masuk dalam jaringan “diperkirakan memuaskan” untuk persyaratan yang diberikan. Pertanyaannya adalah: berapa banyak angka irasional yang Anda tangkap?



Dalam setiap interval dari garis bilangan berisi angka irasional nomor tak hingga, sehingga jumlah pasti angka irasional yang tertangkap tidak dapat ditulis. Sebagai gantinya, ahli matematika berbicara tentang proporsi jumlah total bilangan irasional yang ditangkap oleh setiap fraksi. Mereka mengevaluasi proporsi ini menggunakan konsep seperti "ukuran" dari himpunan bagian angka - itu adalah seperti memperkirakan jumlah ikan yang ditangkap berdasarkan berat daripada kuantitas.

Hipotesis Duffin-Schaffer menyarankan menambahkan semua ukuran himpunan bagian dari bilangan irasional ditangkap oleh masing-masing fraksi yang mendekati. Dia mewakili angka ini sebagai jumlah aritmatika yang besar. Lalu dia membuat prediksi utamanya: jika jumlah ini mencapai tak terhingga, maka Anda mendekati hampir semua bilangan irasional; jika hanya memberikan nilai akhir, terlepas dari berapa banyak ukuran yang telah Anda simpulkan, maka Anda tidak dapat memperkirakan hampir semua nomor irasional.

Pertanyaan serupa, apakah jumlah “menyimpang” hingga tak terbatas atau “menyatu” dengan nilai yang terbatas, muncul dalam banyak bidang matematika. Pernyataan utama hipotesis Duffin-Schaffer adalah bahwa jika Anda ingin memahami apakah Anda dapat mendekati hampir semua bilangan irasional menggunakan seperangkat penyebut dan kesalahan tertentu, maka Anda hanya perlu mengetahui satu hal: apakah jumlah tindakan tak terbatas berbeda hingga tak terbatas, atau bertemu ke nilai akhir.

"Pada akhirnya, tidak peduli bagaimana Anda memutuskan untuk mengevaluasi perkiraan untuk masing-masing penyebut, kesuksesan Anda sepenuhnya tergantung pada satu hal: apakah urutan tanpa akhir menyimpang atau tidak," kata Waaler.

Pengambilan keputusan

Anda mungkin bertanya-tanya: bagaimana jika angka didekati oleh satu fraksi berpotongan dengan angka yang didekati oleh yang lain? Apakah kita tidak akan memperhitungkannya dua kali saat menghitung tindakan?

Untuk beberapa urutan aproksimasi, penghitungan ganda tidak penting. Matematikawan beberapa dekade yang lalu membuktikan bahwa hipotesis ini berlaku untuk urutan perkiraan yang terdiri dari bilangan prima. Tetapi untuk banyak urutan perkiraan lainnya, penghitungan ganda adalah masalah. Karena itu, matematikawan tidak dapat menangani hipotesis ini selama 80 tahun.

Tingkat di mana penyebut yang berbeda menangkap sekumpulan bilangan irasional tercermin dalam jumlah pembagi sederhana yang umum untuk semua penyebut. Pertimbangkan angka 12 dan 35. Pembagi utama dari 12 adalah 2 dan 3. Pembagi utama dari 35 adalah 5 dan 7. Dengan kata lain, faktor prima yang umum dari 12 dan 35 tidak - akibatnya, ada banyak bilangan irasional yang dapat didekati dengan fraksi dari penyebut 12 dan 35 tidak secara khusus berpotongan.

Bagaimana dengan penyebut 12 dan 20? Pada 20, pembagi utama adalah 2 dan 5 berpotongan dengan pembagi 12. Dengan cara yang sama, bilangan irasional yang dapat didekati dengan pecahan dengan penyebut 20 berpotongan dengan yang dapat didekati dengan pecahan dengan penyebut 12. Hipotesis Duffin-Shaffer adalah yang paling sulit untuk dibuktikan. dalam situasi seperti itu - ketika angka-angka dalam urutan aproksimasi memiliki banyak pembagi prime kecil yang umum, dan persimpangan banyak himpunan bagian dari angka yang masing-masing penyebutnya kira-kira terjadi.

"Ketika banyak penyebut yang Anda pilih memiliki banyak pembagi kecil yang sederhana, mereka mulai saling mengganggu," kata Sam Chau dari Oxford.

Kunci untuk menyelesaikan hipotesis adalah menemukan cara untuk secara akurat menghitung saling tumpang tindih himpunan bagian dari angka irasional, yang diperkirakan oleh penyebut yang memiliki pembagi utama yang sama. Selama 80 tahun, tidak ada yang berhasil melakukan ini. Cuculopoulos dan Maynard berhasil, menemukan sudut pandang yang sama sekali baru tentang masalah tersebut.


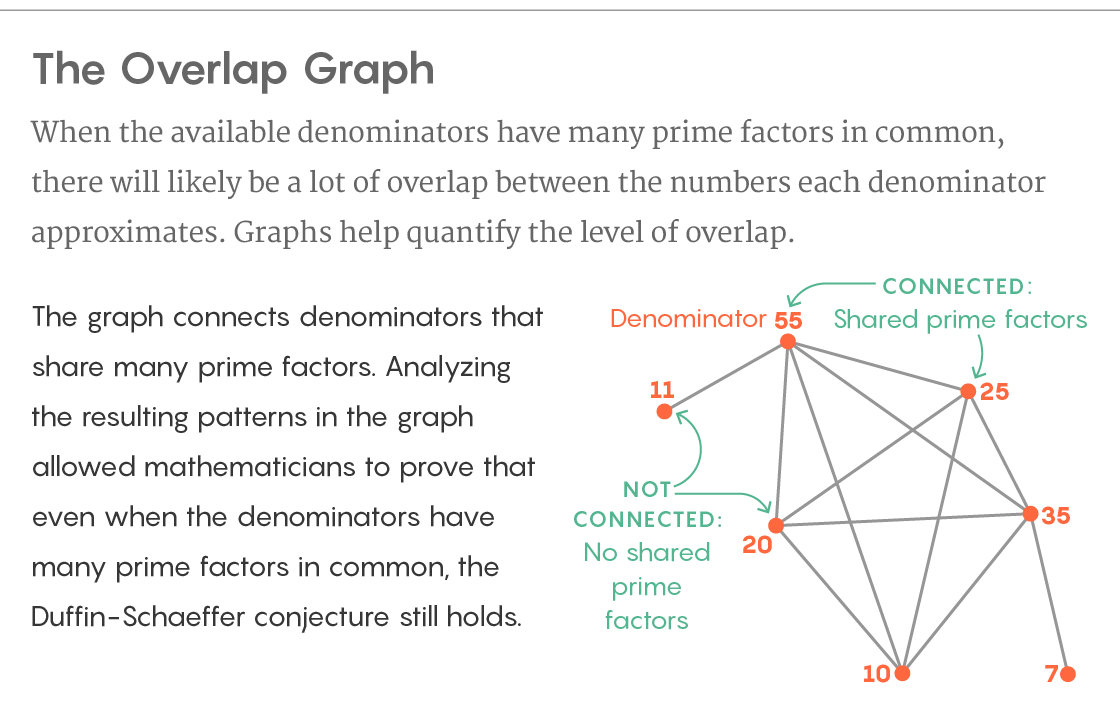Hitungan Hamparan Reksa

Dalam bukti baru mereka, mereka membuat grafik dari penyebutnya. Mereka membangun mereka sebagai simpul dari grafik dan menghubungkan simpul dengan tepi jika mereka memiliki banyak pembagi utama yang sama. Struktur grafik menggambarkan superposisi himpunan bagian dari bilangan irasional yang didekati oleh masing-masing penyebut. Dan meskipun hamparan ini sulit untuk diselidiki secara langsung, Kukulopoulos dan Maynard menemukan cara untuk menganalisis struktur grafik menggunakan alat dari teori grafik - dan informasi yang mereka butuhkan ditemukan dengan cara ini.

"Grafik membantu memahami tugas secara visual, itu adalah bahasa yang indah di mana Anda dapat merenungkan masalah," kata Kukulopulos.

Cuculopoulos dan Maynard membuktikan bahwa hipotesis Duffin-Schaffer memang benar: jika Anda diberi daftar penyebut dengan kesalahan yang valid, Anda dapat menentukan apakah mungkin untuk memperkirakan hampir semua bilangan irasional, atau tidak mungkin untuk melakukan ini hanya dengan memeriksa apakah jumlah tindakan yang sesuai berbeda. hingga tak terbatas atau konvergen ke nilai yang terbatas.

Ini adalah tes yang elegan, mengambil pertanyaan luas tentang sifat aproksimasi dengan bilangan rasional dan menguranginya menjadi satu nilai yang dihitung. Setelah membuktikan universalitas pengujian, Cuculopoulos dan Maynard melakukan salah satu hal terbesar untuk matematika: mereka memberikan jawaban akhir untuk pertanyaan mendasar di bidang mereka.

"Bukti mereka telah menjadi hasil yang perlu dan cukup," kata Green. "Kurasa dia menandai akhir bab selanjutnya dalam matematika."