Clustering adalah bagian penting dari jalur pembelajaran mesin untuk menyelesaikan masalah ilmiah dan bisnis. Ini membantu untuk mengidentifikasi set poin yang terkait erat (ukuran jarak tertentu) di awan data yang mungkin sulit ditentukan dengan cara lain.

Namun, proses pengelompokan untuk sebagian besar berkaitan dengan bidang pembelajaran mesin tanpa guru , yang ditandai dengan sejumlah kesulitan. Tidak ada jawaban atau tips tentang cara mengoptimalkan proses atau mengevaluasi keberhasilan pelatihan. Ini adalah wilayah yang belum dipetakan.

Oleh karena itu, tidak mengherankan bahwa metode populer pengelompokan dengan metode k-rata tidak sepenuhnya menjawab pertanyaan kami: "Bagaimana kita pertama kali mengetahui jumlah cluster?" Pertanyaan ini sangat penting, karena pengelompokan sering mendahului pemrosesan lebih lanjut dari masing-masing kelompok, dan jumlah sumber daya komputasi mungkin tergantung pada penilaian jumlah mereka.

Konsekuensi terburuk dapat muncul dalam bidang analisis bisnis. Di sini, clustering digunakan untuk segmentasi pasar, dan ada kemungkinan bahwa staf pemasaran akan dialokasikan sesuai dengan jumlah cluster. Oleh karena itu, perkiraan jumlah ini yang keliru dapat menyebabkan alokasi sumber daya berharga yang tidak optimal.

Metode siku

Ketika clustering menggunakan metode k-means, jumlah cluster paling sering diperkirakan menggunakan "metode siku" . Ini menyiratkan beberapa eksekusi siklik dari algoritma dengan peningkatan jumlah cluster yang dapat dipilih, serta penundaan selanjutnya dari skor clustering pada grafik, dihitung sebagai fungsi dari jumlah cluster.

Berapa skor ini, atau metrik, yang tertunda pada grafik? Mengapa itu disebut metode siku ?

Grafik tipikal terlihat seperti ini:



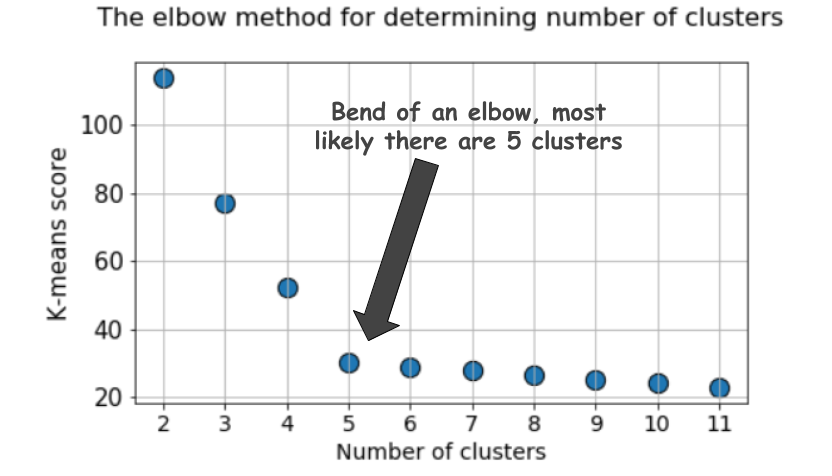
Skor, sebagai suatu peraturan, adalah ukuran dari data input untuk fungsi objektif k-means, yaitu, beberapa bentuk rasio jarak intracluster ke jarak interluster.

Sebagai contoh, metode penilaian ini segera tersedia di alat penilaian k-means di Scikit-learn.

Tetapi perhatikan grafik ini lagi. Rasanya sesuatu yang aneh. Berapa jumlah cluster optimal yang kita miliki, 4, 5 atau 6?

Tidak jelas, kan?

Siluet adalah metrik yang lebih baik

Koefisien siluet dihitung dengan menggunakan jarak intracluster rata-rata (a) dan jarak rata-rata ke kluster terdekat (b) untuk setiap sampel. Siluet dihitung sebagai (b - a) / max(a, b) . Biarkan saya jelaskan: b adalah jarak antara a dan cluster terdekat yang bukan milik a. Anda dapat menghitung nilai siluet rata-rata untuk semua sampel dan menggunakannya sebagai metrik untuk memperkirakan jumlah cluster.

Ini adalah video yang menjelaskan ide ini:


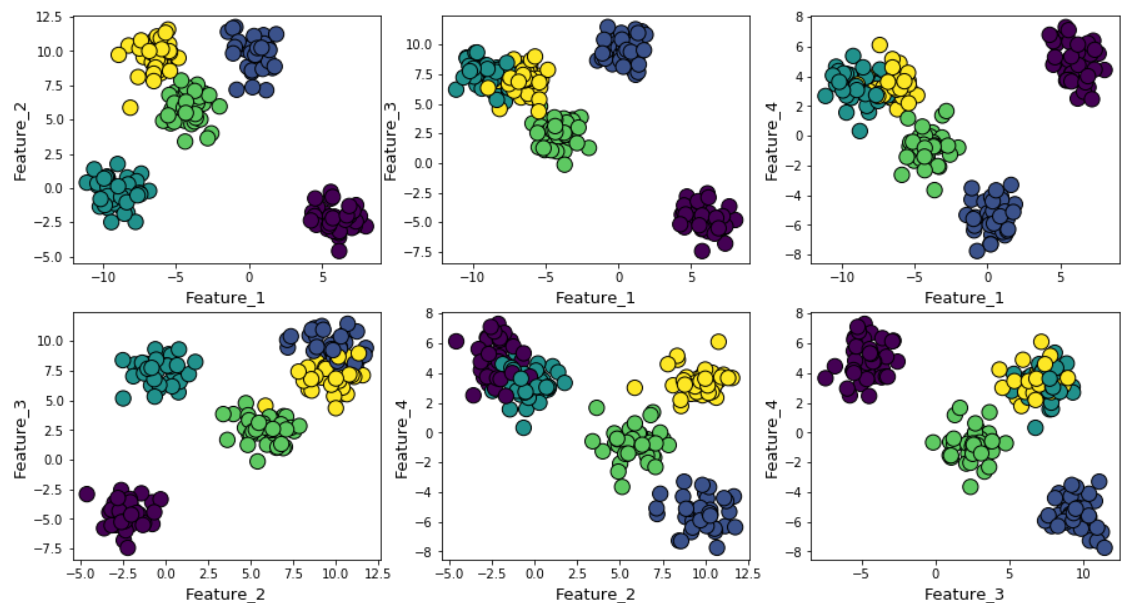
Misalkan kita menghasilkan data acak menggunakan fungsi make_blob dari Scikit-learn. Data terletak di empat dimensi dan sekitar lima pusat cluster. Inti dari masalah adalah bahwa data dihasilkan di sekitar lima pusat cluster. Namun, algoritma k-means tidak tahu tentang ini.

Cluster dapat ditampilkan pada grafik sebagai berikut (tanda berpasangan):



Kemudian kita menjalankan algoritma k-means dengan nilai dari k = 2 hingga k = 12, dan kemudian kita menghitung metrik default untuk k-means dan nilai siluet rata-rata untuk setiap proses, dengan hasil yang ditampilkan dalam dua grafik yang berdekatan.



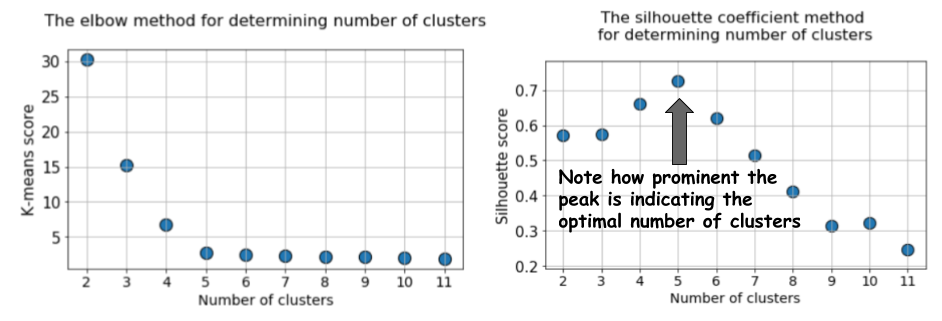
Perbedaannya jelas. Nilai rata-rata siluet meningkat menjadi k = 5, dan kemudian menurun tajam untuk nilai k yang lebih tinggi. Artinya, kita mendapatkan puncak yang diucapkan pada k = 5, ini adalah jumlah cluster yang dihasilkan dalam dataset asli.

Grafik siluet memiliki karakter puncak, berbeda dengan grafik melengkung lembut ketika menggunakan metode siku. Lebih mudah untuk divisualisasikan dan dibenarkan.

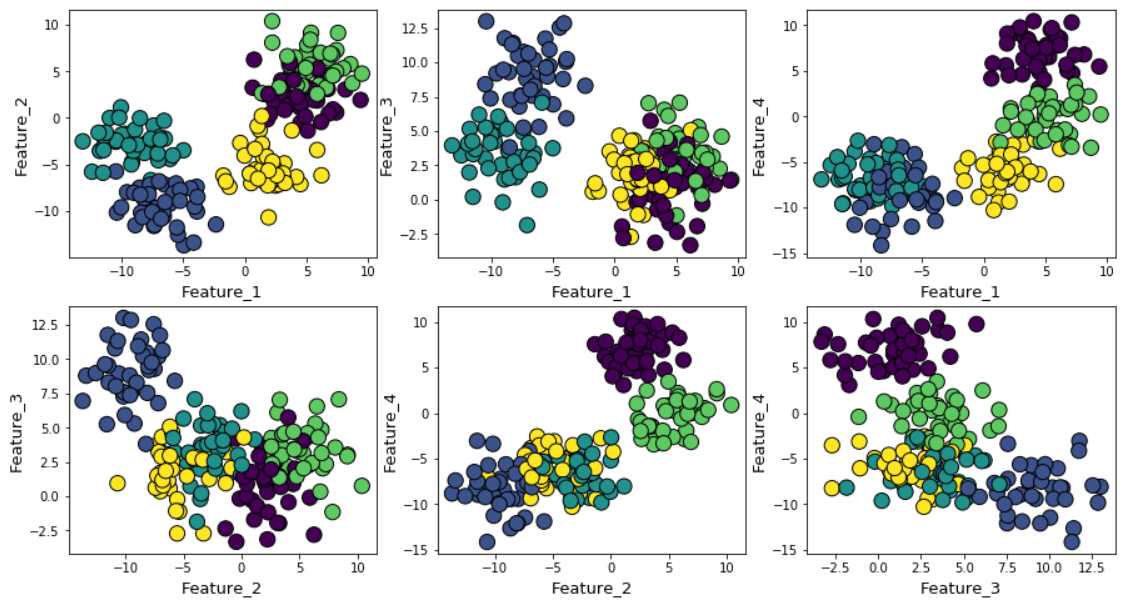
Jika Anda meningkatkan noise Gaussian selama pembuatan data, kluster akan tumpang tindih lebih kuat.



Dalam hal ini, menghitung k-means default menggunakan metode siku memberikan hasil yang lebih tidak pasti. Di bawah ini adalah grafik dari metode siku, di mana sulit untuk memilih titik yang cocok di mana garis benar-benar tertekuk. Apakah 4, 5, 6 atau 7?



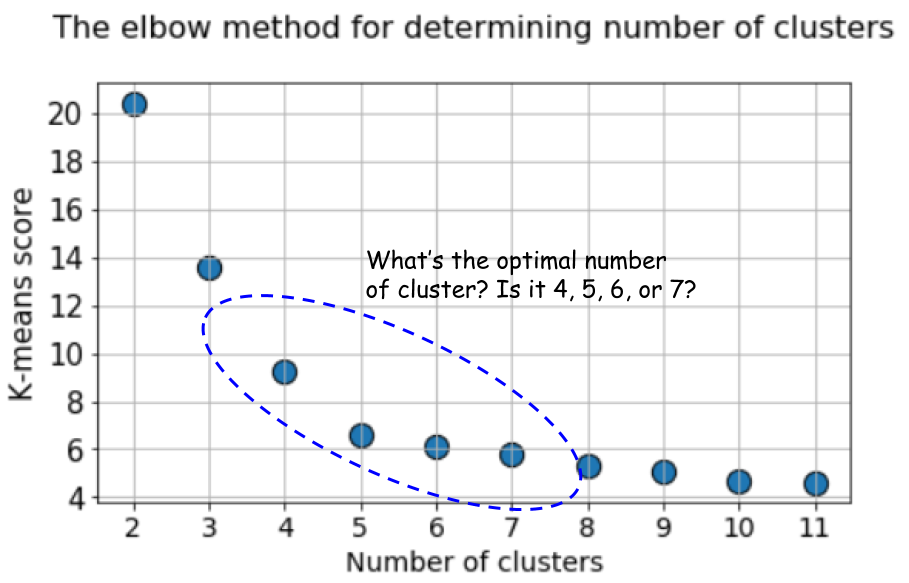
Pada saat yang sama, grafik siluet masih menunjukkan puncak di wilayah 4 atau 5 pusat cluster, yang sangat memudahkan kehidupan kita.

Jika Anda melihat cluster yang tumpang tindih satu sama lain, Anda akan melihat bahwa, terlepas dari kenyataan bahwa kami menghasilkan data di sekitar 5 pusat, karena dispersi yang tinggi, hanya 4 cluster yang dapat dibedakan secara struktural. Siluet dengan mudah mengungkapkan perilaku ini dan menunjukkan jumlah cluster optimal antara 4 dan 5.

Skor BIC dengan model campuran distribusi normal

Ada metrik besar lainnya untuk menentukan jumlah sebenarnya dari cluster, seperti Bayesian Information Criterion (BIC). Tetapi mereka dapat digunakan hanya jika kita perlu beralih dari metode k-means ke versi yang lebih umum - campuran dari distribusi normal (Gaussian Mixture Model (GMM)).

GMM memandang cloud data sebagai superposisi dari sejumlah dataset dengan distribusi normal, dengan nilai rata-rata dan varian yang berbeda. Dan kemudian GMM menggunakan algoritma untuk memaksimalkan harapan untuk menentukan rata-rata dan varian ini.

BIC untuk regularisasi

Anda mungkin sudah menemui BIC dalam analisis statistik atau ketika menggunakan regresi linier. BIC dan AIC (Akaike Information Criterion, kriteria informasi Akaike) digunakan dalam regresi linier sebagai teknik regularisasi untuk proses pemilihan variabel.

Gagasan serupa berlaku untuk BIC. Secara teoritis, cluster yang sangat kompleks dapat dimodelkan sebagai superposisi dari sejumlah besar dataset dengan distribusi normal. Untuk mengatasi masalah ini, Anda dapat menerapkan distribusi yang tidak terbatas jumlahnya.
Tapi ini mirip dengan meningkatkan kompleksitas model dalam regresi linier, ketika sejumlah besar properti dapat digunakan untuk mencocokkan data kompleksitas apa pun, hanya untuk kehilangan kemungkinan generalisasi, karena model yang terlalu rumit sesuai dengan kebisingan, dan bukan dengan pola nyata.

Metode BIC menghasilkan banyak distribusi normal dan mencoba menjaga model cukup sederhana untuk menggambarkan pola yang diberikan.

Oleh karena itu, Anda dapat menjalankan algoritme GMM untuk sejumlah besar pusat cluster, dan nilai BIC akan meningkat ke beberapa titik, dan kemudian mulai menurun saat denda tumbuh.

Ringkasan

Ini buku catatan Jupyter untuk artikel ini. Jangan ragu untuk bercabang dan bereksperimen.

Kami di Jet Infosystems membahas beberapa alternatif metode siku yang populer dalam hal memilih jumlah cluster yang tepat ketika belajar tanpa guru menggunakan algoritma k-means.

Kami memastikan bahwa alih-alih metode siku, lebih baik menggunakan koefisien "siluet" dan nilai BIC (dari ekstensi GMM untuk k-means) untuk secara visual menentukan jumlah cluster optimal.