Namun, mengapa Posit adalah alternatif yang layak untuk IEEE 754

Bulan Posit tentang Habré telah dinyatakan terbuka, yang berarti saya tidak dapat melewati dan mengabaikan kritik yang telah menimpa mereka. Dalam seri sebelumnya:

Pendekatan baru dapat membantu kita menyingkirkan perhitungan floating point
Posit-arithmetic: mengalahkan floating point di bidangnya sendiri. Bagian 1
Posit-arithmetic: mengalahkan floating point di bidangnya sendiri. Bagian 2
Tantangan Posisi Dewasa

Saya pikir banyak dari Anda dapat segera mengingat setidaknya satu kasus dari sejarah ketika ide-ide revolusioner pada saat pembentukannya mendapat penolakan dari komunitas pakar. Sebagai aturan, kesalahan perilaku tersebut adalah beban besar dari pengetahuan yang sudah terakumulasi yang tidak memungkinkan untuk melihat masalah lama dengan cara baru. Dengan demikian, ide baru kehilangan dalam hal karakteristik untuk pendekatan yang ditetapkan, karena hanya dievaluasi oleh metrik yang dianggap penting pada tahap pengembangan sebelumnya.

Inilah tepatnya keengganan yang dihadapi format Posit saat ini: para kritikus sering kali “melihat ke arah yang salah” dan bahkan menggunakan Posit dalam eksperimen mereka dengan cara yang salah. Pada artikel ini saya akan mencoba menjelaskan alasannya.

Kelebihan dari Posit telah disebutkan sedikit: keanggunan matematis, akurasi tinggi pada nilai-nilai dengan eksponen rendah, kisaran nilai yang luas, hanya satu representasi biner dari NaN dan nol, tidak adanya nilai-nilai subnormal, perlawanan terhadap overflow / underflow. Kritik telah diungkapkan cukup sedikit: akurasi yang tidak berguna untuk nilai yang sangat besar atau sangat kecil, format representasi biner yang kompleks dan, tentu saja, kurangnya dukungan perangkat keras.

Saya tidak ingin mengulangi argumen yang telah saya katakan, sebagai gantinya, saya akan mencoba untuk fokus pada aspek yang, sebagai aturan, diabaikan.

Aturan gim telah berubah

Standar IEEE 754 menjelaskan angka floating point yang diterapkan di Intel 8087 hampir 40 tahun yang lalu. Dengan standar industri kami, ini adalah waktu yang luar biasa; semuanya telah berubah sejak saat itu: kinerja prosesor, biaya memori, volume data, dan skala perhitungan. Format Posit dikembangkan tidak hanya sebagai versi terbaik IEEE 754, tetapi sebagai pendekatan untuk bekerja dengan angka yang memenuhi persyaratan baru saat itu.

Tugas tingkat tinggi tetap sama - kita semua membutuhkan perhitungan yang efektif di bidang bilangan rasional dengan kehilangan akurasi minimal. Tetapi kondisi di mana tugas sedang diselesaikan secara radikal berubah.

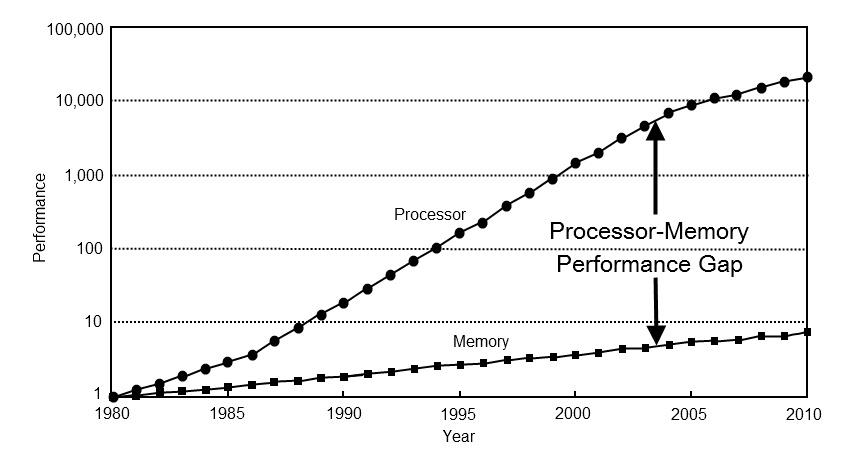
Pertama, prioritas untuk optimasi telah berubah. 40 tahun yang lalu, kinerja komputer hampir seluruhnya bergantung pada kinerja prosesor. Saat ini, kinerja sebagian besar komputasi terletak pada memori. Untuk memverifikasi ini, lihat saja bidang utama pengembangan prosesor beberapa dekade terakhir: caching tiga tingkat, eksekusi spekulatif, pipelining perhitungan, prediksi cabang. Semua pendekatan ini ditujukan untuk mencapai kinerja tinggi dalam kondisi komputasi cepat dan akses memori yang lambat.



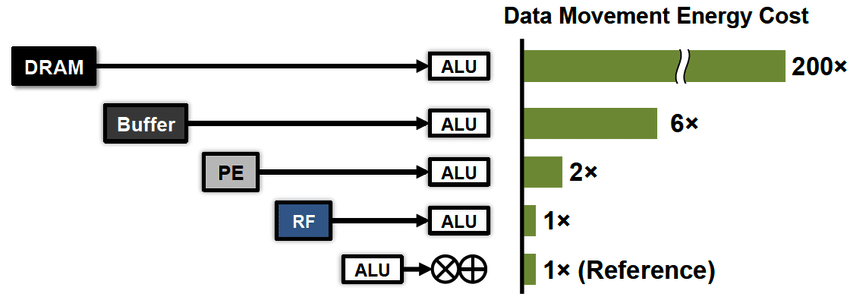
Kedua, persyaratan baru telah muncul untuk konsumsi energi kedepan yang efektif. Selama beberapa dekade terakhir, teknologi penskalaan horisontal untuk komputasi telah berkembang sangat pesat sehingga kami mulai tidak terlalu peduli dengan kecepatan perhitungan ini, tetapi tentang tagihan listrik. Di sini saya harus menekankan bagian penting untuk dipahami. Dari sudut pandang efisiensi energi, perhitungannya murah, karena register prosesor sangat dekat dengan komputernya. Akan jauh lebih mahal untuk membayar transfer data, baik antara prosesor dan memori (x100), dan jarak jauh (x1000 ...).



Berikut ini hanya satu contoh proyek sains yang berencana digunakan Posit:



Jaringan teleskop ini menghasilkan 200 petabyte data per detik, yang prosesnya membutuhkan daya dari pembangkit listrik kecil - 10 megawatt . Jelas, untuk proyek seperti itu, pengurangan data dan konsumsi energi sangat penting.

Sampai awal

Jadi apa yang ditawarkan oleh standar Posit? Untuk memahami ini, Anda harus kembali ke awal diskusi dan memahami apa yang dimaksud dengan ketepatan angka floating point.

Sebenarnya ada dua aspek berbeda yang terkait dengan akurasi. Aspek pertama adalah keakuratan perhitungan - berapa banyak hasil perhitungan menyimpang selama berbagai operasi. Aspek kedua adalah keakuratan presentasi - seberapa jauh nilai aslinya terdistorsi pada saat konversi dari bidang bilangan rasional ke bidang bilangan apung dari format tertentu.

Sekarang akan ada momen penting untuk kesadaran. Posit terutama merupakan format untuk mewakili angka-angka rasional, bukan cara untuk melakukan operasi pada mereka. Dengan kata lain, Posit adalah format kompresi rasional yang hilang. Anda mungkin pernah mendengar klaim bahwa Posit 32-bit adalah alternatif yang baik untuk Float 64-bit. Jadi, kita berbicara tentang mengurangi separuh jumlah data yang diperlukan untuk menyimpan dan mengirimkan set angka yang sama. Memori dua kali lebih sedikit - konsumsi daya hampir 2 kali lebih sedikit dan kinerja prosesor tinggi karena harapan yang lebih rendah dari akses memori.

Ujung kedua tongkat

Di sini Anda harus memiliki pertanyaan logis: apa gunanya mewakili bilangan rasional secara efisien jika tidak memungkinkan perhitungan dilakukan dengan akurasi tinggi.

Bahkan, ada cara untuk melakukan perhitungan yang tepat, dan itu disebut Quire. Ini adalah format lain untuk merepresentasikan bilangan rasional, yang terkait erat dengan Posit. Tidak seperti Posit, format Quire dirancang khusus untuk perhitungan dan untuk menyimpan nilai-nilai perantara dalam register, dan tidak dalam memori utama.



Singkatnya, Quire tidak lebih dari baterai integer lebar (aritmatika titik tetap). Unit, sebagai representasi biner dari Quire, sesuai dengan nilai positif minimum Posit. Nilai Quire maksimum sesuai dengan nilai Posit maksimum. Setiap nilai Posit memiliki representasi unik di Quire tanpa kehilangan keakuratan, tetapi tidak setiap nilai Quire dapat diwakili dalam Posit tanpa kehilangan keakuratan.

Manfaat Quire jelas. Mereka memungkinkan Anda untuk melakukan operasi dengan akurasi yang jauh lebih tinggi daripada Float, dan untuk operasi penambahan dan multiplikasi tidak akan ada kehilangan akurasi sama sekali. Harga yang harus Anda bayar untuk ini adalah register prosesor lebar (Posit 32-bit dengan es = 2 sesuai dengan Quire 512-bit), tetapi ini bukan masalah serius bagi prosesor modern. Dan jika 40 tahun yang lalu menghitung lebih dari 512 bit integer tampaknya merupakan kemewahan yang tidak dapat diterima, saat ini itu merupakan alternatif yang memadai untuk akses luas ke memori.

Menyatukan puzzle

Dengan demikian, Posit menawarkan tidak hanya standar baru dalam bentuk alternatif untuk Float / Double, tetapi lebih merupakan pendekatan baru untuk bekerja dengan angka. Tidak seperti Float - yang merupakan representasi tunggal yang berusaha menemukan kompromi antara akurasi dan efisiensi penyimpanan dan efisiensi komputasi, Posit menawarkan dua format presentasi yang berbeda, satu untuk menyimpan dan mentransmisikan angka - Posit sendiri, dan yang lainnya untuk perhitungan dan perantaranya Nilai - Quire.

Ketika kami memecahkan masalah praktis menggunakan angka floating point, dari sudut pandang prosesor, bekerja dengan mereka dapat direpresentasikan sebagai serangkaian tindakan berikut:

1. Baca nilai angka dari memori.
2. Lakukan beberapa urutan operasi. Terkadang jumlah operasi cukup besar. Dalam hal ini, semua nilai menengah dari perhitungan disimpan dalam register.
3. Tulis hasil operasi ke memori.

Dengan Float / Double, akurasi hilang di setiap operasi. Dengan Posit + Quire, hilangnya keakuratan selama perhitungan dapat diabaikan. Itu hilang hanya pada tahap terakhir, pada saat mengubah nilai Quire ke Posit. Itulah sebabnya sebagian besar masalah "akumulasi kesalahan" untuk Posit + Quire sama sekali tidak relevan.

Tidak seperti Float / Double, ketika menggunakan Posit + Quire, kita biasanya bisa mendapatkan representasi angka yang lebih kompak. Akibatnya - akses lebih cepat ke data dari memori (kinerja lebih baik) dan penyimpanan dan transmisi informasi yang lebih efisien.

Rasio Mueller

Sebagai demonstrasi visual, saya hanya akan memberikan satu contoh - relasi pengulangan Muller klasik, yang diciptakan secara khusus untuk menunjukkan bagaimana akumulasi kesalahan dalam perhitungan floating point secara radikal mendistorsi hasil perhitungan.



Dalam hal menggunakan aritmatika dengan presisi arbitrer, urutan perulangan harus dikurangi menjadi nilai 5. Dalam kasus aritmatika titik apung, pertanyaannya adalah hanya pada iterasi mana hasil perhitungan akan mulai memiliki deviasi yang tidak cukup besar.

Saya melakukan percobaan untuk IEEE 754 dengan presisi tunggal dan ganda, serta untuk Posit + Quire 32-bit. Perhitungan dilakukan dalam aritmatika Quire, tetapi setiap nilai dalam tabel dikonversi ke Posit.


Seperti yang dapat Anda lihat dari tabel, Float 32-bit sudah menyerah pada nilai ketujuh, dan Float 64-bit bertahan hingga iterasi ke-14. Pada saat yang sama, perhitungan untuk Posit menggunakan Quire mengembalikan hasil yang stabil hingga 58 iterasi!

Akhlak

Untuk banyak kasus praktis dan ketika digunakan dengan benar, format Posit akan benar-benar memungkinkan Anda menghemat memori di satu sisi, mengompresi angka lebih baik daripada Float, dan di sisi lain memberikan akurasi perhitungan yang lebih baik berkat Quire.

Tapi ini hanya teori! Ketika datang ke akurasi atau kinerja, selalu mengambil tes sebelum membabi buta percaya satu pendekatan atau yang lain. Memang, dalam praktiknya, kasus khusus Anda akan menjadi luar biasa lebih sering daripada dalam teori.

Yah, jangan lupa hukum pertama Clark (interpretasi gratis): Ketika seorang ahli yang dihormati dan berpengalaman mengklaim bahwa ide baru akan berhasil, dia hampir pasti benar. Ketika dia mengklaim bahwa ide baru itu tidak akan berhasil, maka dia sangat mungkin salah. Saya tidak menganggap diri saya seorang ahli yang berpengalaman untuk memungkinkan Anda mengandalkan pendapat saya, tetapi saya meminta Anda untuk berhati-hati dalam mengkritik orang-orang yang berpengalaman dan dihormati sekalipun. Lagipula, iblis ada dalam rinciannya, dan bahkan orang yang berpengalaman pun dapat merindukan mereka.