Jumlah Masalah

Dalam tugas terkenal dengan koin, yang perlu menghitung perubahan, seperti yang Anda tahu, ada dua masalah .
- Yang pertama adalah jumlah denominasi koin,
- yang kedua adalah jumlah digit yang mewakili perubahan.
Dan kedua kuantitas ini memiliki efek eksponensial pada beban mesin Turing, yang sebenarnya terlibat dalam perhitungan.
Mengakui bahwa seseorang memiliki dua ketergantungan sekaligus tidak diterima bahkan dalam masyarakat pecandu alkohol. Karena itu, saya memutuskan untuk memainkannya dengan aman dan menyingkirkan salah satu masalah ini sebelumnya. Cara ini akan menjadi jumlah denominasi koin.

Singkatnya, esensi masalah dijelaskan sebagai berikut: ketergantungan eksponensial. Yaitu, pelepasan koin jenis baru dari denominasi yang tidak ada mensyaratkan peningkatan ganda dalam jumlah kombinasi koin. Denominasi lain - dua kali lipat, dan seterusnya hingga tak terbatas bersyarat. Dengan inflasi yang deras, ketika koin / uang kertas baru diterbitkan cukup sering, Anda harus membeli komputer yang lebih kuat untuk menyelesaikan masalah. Dan di mana mendapatkan uang untuk itu dengan inflasi yang deras?

Jadi, solusi yang sebenarnya cukup sederhana.
Jika Anda membayangkan segmen dari nol hingga C (ubah) dengan titik-titik di atasnya sesuai dengan denominasi koin, maka setiap orang cerdas akan melihat kira-kira gambar berikut:

Yah, mungkin dengan warna berbeda.
Jadi apa yang bisa kita katakan tentang titik merah? Tentu saja, fakta bahwa angka yang sesuai dengan poin ini adalah jumlah yang dapat kita berikan dalam bentuk perubahan. Dan dengan satu koin. Mungkin seseorang melihat sesuatu yang lain, tetapi saya, sebagai seorang seniman, menginvestasikan dengan tepat makna ini. Dan, sebagai seorang seniman, saya akan menggambar titik lain dalam gambar ini yang sesuai dengan jumlah titik pertama (dari kiri ke kanan) dengan titik yang sama (semuanya benar: itu akan menggandakan nilai nominal). Saya menggambar dalam warna yang sama, karena titik baru berarti hal yang sama - jumlah ini juga bisa menjadi perubahan.

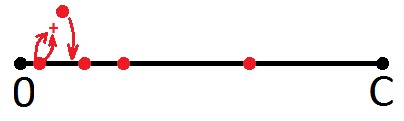
Selanjutnya, saya mengambil poin pertama dan merangkum dengan yang kedua, bahkan jika poin kedua adalah jumlah sebelumnya (ini tidak masalah, karena semua poin sama di sini). Saya akan menempatkan poin baru di segmen lagi.

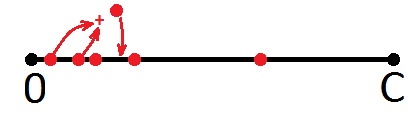
Jika titik baru melampaui batas segmen, maka kami tidak menggambar apa pun, tetapi kembali ke awal segmen dan mengambil titik berikutnya, yaitu, yang kedua. Lebih jauh sama (dari kiri ke kanan).
Sebenarnya, ketika titik C (saya ingatkan Anda, ini adalah perubahan) berubah menjadi merah, kita dapat mengasumsikan bahwa solusi telah ditemukan. Dan Anda dapat melalui siklus penuh dan menemukan solusi optimal, sehingga jumlah koin minimal.

Dari sudut pandang pemrograman , ada dua siklus. Yang pertama adalah dari 0 hingga C / 2 (tidak perlu mengambil titik pertama dari C / 2 yang lebih besar, karena titik kedua selalu lebih besar dari yang pertama dan secara total mereka akan melampaui batas-batas segmen). Siklus kedua dibangun ke dalam siklus pertama, dimulai dari titik yang sama dengan siklus eksternal menunjuk ke dan sampai penjumlahan meninggalkan batas-batas segmen.
Sebenarnya, ini adalah kegagalan: kami tidak kehilangan satu opsi, dan kami dijamin akan menemukan solusi optimal, atau kami akan menyimpulkan bahwa tidak ada solusi.

Mari kita hitung jumlah iterasi di dalam loop kita. Dalam siklus eksternal adalah C / 2, dalam siklus internal hampir sama. Kalikan C / 2 * C / 2 = (C ^ 2) / 4. Bulat ke C kuadrat. Ini adalah opsi terburuk ketika seluruh segmen kami hanya terdiri dari titik-titik merah. Jika ada spasi di antara titik-titik, jumlah iterasi akan berkurang secara signifikan.
Seperti yang Anda lihat, ketika menentukan kesulitan memecahkan masalah, kami tidak menggunakan jumlah denominasi koin. Nilai ini tidak secara langsung mempengaruhi kompleksitas solusi. Nilai-nilai dari denominasi-denominasi ini memengaruhi, katakanlah 1 sen koin dan membuat segmen ini sepenuhnya merah. Oleh karena itu, lebih baik untuk tidak memperhitungkan koin ini, dan pada akhir keputusan, ambil titik merah terdekat dengan C dan buat sketsa di atas satu sen. Tapi ini sudah menjadi momen optimalisasi algoritma, dan itu berada di luar cakupan artikel ini.

Sebenarnya itulah yang ingin saya katakan. Versi program yang berfungsi dapat ditemukan di sini: tautan github

1. Dalam file init.h, setel COINS_NUMBER - jumlah denominasi koin, dan AMOUNT - jumlah perubahan.
2. Dalam file coinc.c tentukan denominasi koin dalam array koin.
3. Di Linux, jalankan make_sh.
4. Jalankan program aplikasi untuk dieksekusi


Biarkan saya memberi Anda beberapa contoh lucu. Bayangkan bahwa di beberapa negara, matematikawan berkuasa dan mengedarkan 32 denominasi koin: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. Untuk kenyamanan penghitungan, hanya bilangan prima yang dipilih (yah, bukankah itu lucu ?). Dan untuk memastikan bahwa reformasi moneter berhasil, mereka mengirim kurir di toko kurir untuk menukar tagihan 5333 (juga nomor utama). Kasir pada solusi single-core lama memecahkan masalah: 39 koin dengan nilai nominal 131 Pythagoras, satu koin 127 dan satu 97. Perhitungannya memakan waktu 3 detik dan sedikit lebih dari satu megabyte memori. Pemerintah diberitahu bahwa rakyat puas dengan reformasi, ia percaya dengan cepat.


Dan contoh yang sedikit lebih sulit untuk diverifikasi. Koin, seratus denominasi dalam urutan yang aneh: 0101, 0202, 0303 ... 9898, 9999, 100100. Jumlah perubahan: 101010. Pencarian untuk solusi memerlukan waktu 1 detik dan sedikit lebih dari satu megabita memori. Tetapi keputusan itu, pada kenyataannya, tidak, yaitu, tidak mungkin untuk mengumpulkan jumlah seperti itu dengan koin semacam itu. Dengan koin yang sama, cek 1 juta akan memakan waktu 26 megabyte dan ratusan detik, yang menunjukkan ketergantungan eksponensial pada jumlah, tetapi bukan jumlah denominasi koin.