Apa yang ada di balik konstanta Feigenbaum

Obituari: Mitchell Feigenbaum, (1944-2019), 4.66920160910299067185320382 ...

Steven Wolfram Artikel Blog



Ini disebut konstanta Feigenbaum dan sama dengan sekitar 4,6692016. Dan itu terjadi dengan periodisitas yang patut ditiru dalam beberapa jenis sistem matematika - dan fisik - yang dapat menunjukkan perilaku kacau.

Mitchell Feigenbaum , yang meninggalkan kami pada tanggal 30 Juni pada usia 74, adalah orang yang menemukannya - pada tahun 1975, dan ia melakukan ini dengan melakukan matematika eksperimental pada kalkulator saku.

Penemuan ini telah menjadi penentu dalam teori chaos . Tetapi ketika pertama kali ditemukan, hasil ini tidak terduga, aneh, tidak terkait dengan apa pun dari apa yang dipelajari sebelumnya. Namun, dalam beberapa hal, fakta bahwa Mitchell Feigenbaum yang menemukan saya selama hampir 40 tahun merasa cocok.

Mitchell, yang mempelajari fisika teoretis, dan seorang ahli tradisi matematika, sepertinya selalu menganggap dirinya orang luar. Dia tampak sedikit seperti Beethoven - dan membuat kesan elegan tentang rahasia intelektual tertentu. Dia sering membuat pernyataan yang kuat, biasanya dengan tampilan konspirasi, dengan sinar di matanya dan segelas anggur atau sebatang rokok di tangannya.

Dia berbicara dalam kalimat panjang berukir yang mengkhianati beasiswa dan intelektual dalam dirinya. Tetapi ide-ide darinya menuangkan yang paling berbeda. Terkadang mereka rinci dan teknis. Kadang-kadang ini lompatan intuisi, yang, setidaknya, saya tidak bisa melacaknya. Dia selalu membaca sesuatu, tidak tidur sampai 5-6 jam, mengisi halaman kuning notebook dengan formula dan memuat sistem Mathematica dengan perhitungan aljabar kompleks yang bisa bertahan berjam-jam.

Ia menerbitkan sedikit, dan karya yang diterbitkan sering mengecewakannya dengan fakta bahwa tidak banyak orang yang memahaminya. Pada saat kematiannya, dia telah bekerja selama bertahun-tahun pada optik persepsi, dan pada pertanyaan seperti "mengapa bulan tampak lebih besar ketika berada di atas cakrawala." Namun, dia tidak memutuskan untuk menerbitkan hal seperti itu.

Selama lebih dari 30 tahun, pekerjaan resmi Mitchell (yang ia terima, pada kenyataannya, karena pembukaan konstanta Feigenbaum) adalah seorang profesor di Universitas Rockefeller di New York (untuk memenuhi misi penelitian biologi Institut, ia diangkat sebagai kepala "Laboratorium Fisika Matematika"). Namun, ia masih melakukan banyak pekerjaan, memberikan namanya pada startup komputasi keuangan, dan terkait erat dengan penemuan metode kartografi baru untuk atlas global Hammond .

Apa yang ditemukan Mitchell

Ide dasarnya cukup sederhana. Ambil angka x dari 0 hingga 1. Kami secara bertahap akan mengganti x dengan kapak (1 - x). Misalkan kita mulai dengan x = 1/3, dan a = 3.2. Maka di sini adalah nilai urut x yang akan kita dapatkan:



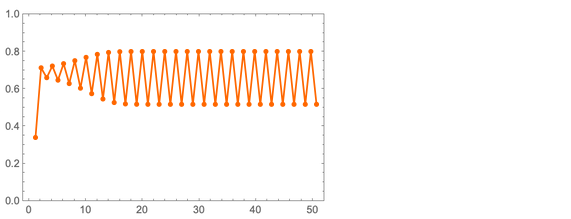
Nilai x dengan cepat menjadi periodik, dengan periode 2. Tapi apa yang terjadi jika kita mengambil nilai lain dari a? Berikut adalah beberapa hasil untuk yang disebut "Pemetaan logistik":



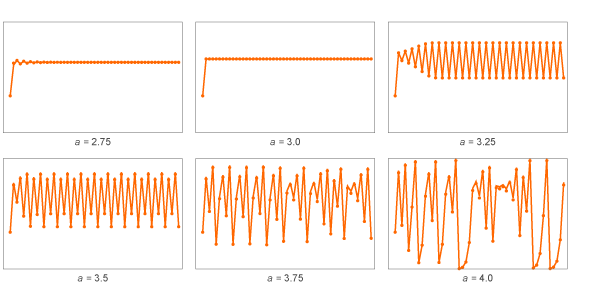
Untuk a kecil, nilai x dengan cepat mencapai nilai tetap. Untuk a besar, mereka menjadi periodik, pertama dengan periode 2, lalu 4. Dan untuk a lebih besar, nilai-nilai mulai melompat dengan cara yang tampaknya acak.

Ini dapat diringkas dengan membangun nilai x (di sini ada 300, setelah menjatuhkan 50 pertama) sebagai fungsi dari nilai a:



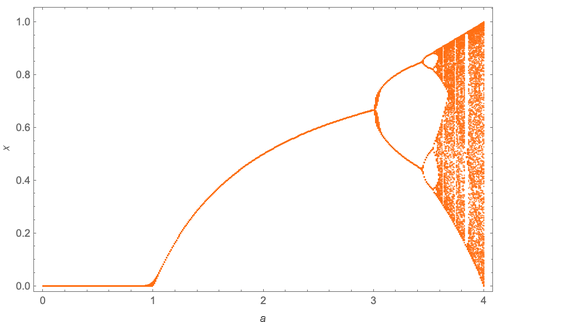
Dengan meningkatnya a, kaskade periode penggandaan diamati. Dalam hal ini, mereka terjadi pada a = 3, a ≈ 3.449, a ≈ 3.544090, a ≈ 3.5644072. Mitchell mencatat bahwa nilai-nilai berturut-turut ini memiliki batas (a ≈ ≈ 3,569946) dalam urutan geometris, a _∞ - a _n ~ δ ^-n dan δ ≈ 4,669.

Hasil yang menarik. Tapi inilah yang memberi makna: ini benar tidak hanya untuk pemetaan iteratif tertentu x → kapak (1 - x); Ini berlaku untuk tampilan apa pun. Di sini, misalnya, adalah "diagram bifurkasi" untuk untuk x → dosa (π √x):



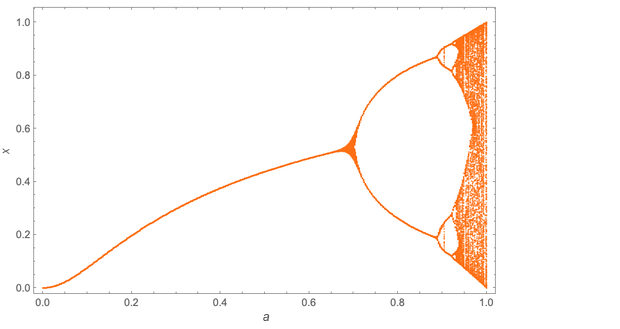
Detailnya berbeda, tetapi Mitchell mencatat bahwa pengaturan periode penggandaan kembali membentuk urutan geometris dengan basis yang persis sama δ ≈ 4.669.

Dan tidak hanya berbagai pemetaan berulang ini memberikan hasil yang serupa secara kualitatif; saat mengukur tingkat konvergensi, ternyata persis sama - selalu δ ≈ 4,669. Ini adalah penemuan hebat Mitchell: fitur universal kuantitatif dari pendekatan kekacauan di kelas sistem.

Latar belakang ilmiah

Ide dasar pemetaan berulang memiliki sejarah panjang sejak zaman kuno. Versi awal mereka muncul sehubungan dengan pencarian untuk perkiraan berturut-turut, misalnya, dari akar kuadrat. Misalnya, metode Newton dari abad ke-17 √2 dapat diperoleh dengan iterasi x → 1 / x + x / 2. Mulai dari x = 1:



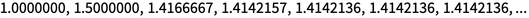
Gagasan tentang pendekatan iteratif fungsi sewenang-wenang pertama kali diformalkan, pada paper tahun 1870 oleh Ernst Schroeder (dikenal karena memformalkan banyak hal, dari derajat ke aljabar Boolean), meskipun sebagian besar diskusi berkaitan dengan solusi persamaan fungsional dan bukan iterasi sendiri (kecuali untuk penelitian ini). area konvergensi dari pendekatan Newton yang dilakukan oleh Arthur Cayley pada tahun 1879). Pada tahun 1918, Gaston Maurice Julia melakukan studi ekstensif tentang fungsi material iteratif pada bidang kompleks, menciptakan set Julia . Tapi sebelum munculnya fraktal pada akhir 1970-an (yang segera menyebabkan munculnya set Mandelbrot ), bidang matematika ini tumbuh.

Tetapi terlepas dari penelitian dalam matematika murni, pemetaan berulang dengan bentuk yang mirip dengan x → kapak (1 - x) mulai muncul pada tahun 1930-an di antara model-model praktis yang mungkin untuk mempelajari biologi populasi atau teori siklus bisnis. Mereka biasanya muncul dalam bentuk versi persamaan kontinu diskrit, seperti persamaan logistik Verhulst pertengahan abad ke-19. Perilaku berosilasi juga umum - dan pada tahun 1954, William Ricoeur (salah satu pendiri memancing ilmiah) juga menemukan perilaku yang lebih kompleks ketika beralih melalui kurva reproduksi ikan empiris.

Dalam matematika murni, varian pemetaan iteratif secara berkala muncul dalam teori bilangan. Pada 1799, Karl Friedrich Gauss , pada kenyataannya, mempelajari pemetaan x → frac (1 / x) sehubungan dengan fraksi lanjutan. Sejak akhir abad ke-19, minat telah muncul dalam pemetaan bentuk x → frac (kapak) dan hubungannya dengan sifat-sifat a.

Segera setelah karya Henri Poincaré mengenai metode efektif mekanika selestial pada tahun 1900-an, muncul gagasan sensitivitas terhadap kondisi awal, dan pada akhirnya diketahui bahwa peta iteratif dapat, pada kenyataannya, “menggali angka” dalam kondisi awal. Misalnya, iterasi x → frac (10 x) lebih dari π digit pada dasarnya hanya menggeser urutan digit satu posisi ke kiri dengan setiap langkah:





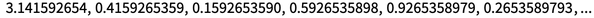
Pemetaan tipe x → kapak (1-x) juga menunjukkan “penggalian angka” yang serupa (misalnya, jika x diganti oleh sin (π u) ² , maka x → 4 x (1-x) berubah menjadi u → frac (u , 2), dan ini dikenal kembali pada tahun 1940-an - misalnya, John von Neumann mengomentari ini pada tahun 1949 sehubungan dengan metode mid-square berulang untuk menghasilkan angka pseudorandom oleh komputer.

Namun, bagaimana dengan matematika eksperimental yang didasarkan pada pemetaan berulang? Hampir tidak ada matematika eksperimental pada komputer digital awal (waktu komputer kebanyakan dari mereka terlalu mahal). Tetapi setelah proyek Manhattan di Los Alamos, mereka menciptakan komputer MANIAC mereka sendiri, yang akhirnya mulai digunakan untuk serangkaian studi di bidang matematika eksperimental. Pada tahun 1964, Paul Stein dan Stan Ulam menulis sebuah laporan berjudul "Mempelajari Transformasi Nonlinier pada Komputer Elektronik," yang menunjukkan foto-foto layar MANIAC yang mirip dengan layar osiloskop dan yang menunjukkan tampilan berulang dari bentuk yang agak rumit. Pada tahun 1971, laporan lain yang dibuat di Los Alamos "karena keingintahuan semata" (ditulis oleh Nick Metropolis, kepala proyek MANIAC dan pengembang metode Monte Carlo, serta Paul Stein dan saudaranya Miron Stein), menghasilkan hasil komputasi yang lebih spesifik untuk pemetaan logistik , dan mencatat fenomena dasar penggandaan periode (penulis menyebutnya urutan-U), serta resistensi kualitatif terhadap perubahan metode tampilan yang mendasarinya.

Terlepas dari semua ini dalam fisika dan matematika ada perkembangan lainnya. Pada tahun 1964, Ed Lorenz (ahli meteorologi dari MIT) memperkenalkan dan menciptakan simulasi persamaan diferensial "alami" namanya, di mana kepekaan terhadap kondisi awal ditunjukkan. Sejak 1940-an, aliran terus menerus perkembangan matematika dalam teori sistem dinamik telah terbentuk (karya didasarkan pada prestasi Poincare dari tahun 1900-an). Secara khusus, mereka menyelidiki sifat global dari solusi persamaan diferensial. Biasanya, peneliti menemukan titik tetap, terkadang membatasi siklus. Namun, pada tahun 1970-an, terutama setelah kemunculan simulasi komputer pertama (seperti pada Lorentz), menjadi jelas bahwa sesuatu yang lain dapat terjadi dengan persamaan nonlinier: yang disebut " Penarik aneh ." Dan ketika mempelajari "pemetaan kembali" dari para penarik aneh, pemetaan berulang mulai muncul lagi.

Namun, baru pada tahun 1975 berbagai studi tentang pemetaan iteratif mulai berpotongan. Di bidang matematika murni, ahli teori sistem dinamik Jim York dan muridnya Tien-Yen Lee dari University of Maryland menerbitkan karya “Chaos follow from period three”, di mana mereka menunjukkan bahwa pemetaan berulang dengan nilai parameter tertentu, kondisi awal yang mengarah ke penampilan siklus tiga panjang , harus ada kondisi awal lainnya yang tidak mengarah pada munculnya siklus - atau, seperti yang mereka gambarkan, menunjukkan kekacauan. Kemudian ternyata bahwa Alexander Sarkovsky, perwakilan dari sekolah Soviet sistem penelitian yang dinamis, kembali pada tahun 1962, terbukti hasil yang sedikit lebih lemah, di mana siklus dengan semua periode mengikuti dari siklus dengan periode 3.

Pada saat yang sama, minat spesialis yang berorientasi matematis dalam biologi populasi mulai tumbuh dalam pemetaan logistik, dari mana ulasan 1976 yang ditulis dengan baik, Model Matematika Sederhana dengan Dynamics Sangat Kompleks, lahir, ditulis oleh seorang ahli fisika Australia yang dididik oleh Robert May , yang pada waktu itu adalah seorang profesor biologi di Princeton (kemudian ia akan menjadi penasihat ilmiah untuk pemerintah Inggris dan menerima gelar Baron May of Oxford).

Tetapi meskipun ada hal-hal seperti sketsa diagram bifurkasi, penemuan sifat numerik universal mereka harus mengharapkan penampilan Mitchell Feigenbaum.

Perjalanan Mitchell

Mitchell Feigenbaum tumbuh di Brooklyn, New York. Ayahnya adalah seorang ahli kimia analitik, dan ibunya mengajar di sekolah umum. Mitchell tidak terlalu suka belajar, meskipun ia menerima nilai bagus dalam ujian matematika dan ilmu eksakta, dan juga belajar matanalisis secara mandiri dan bermain piano. Pada tahun 1960, pada usia 16 tahun, ia, seperti beberapa anak ajaib, memasuki perguruan tinggi kota New York, secara resmi untuk belajar teknik elektro, tetapi juga menghadiri kursus fisika dan matematika. Setelah lulus pada 1964, ia masuk MIT. Awalnya dia ingin mempertahankan gelar doktor di bidang teknik elektro, tetapi dengan cepat beralih ke fisika.

Dan meskipun ia senang dengan fisika matematika klasik (seperti yang disajikan, misalnya, dalam buku Landau dan Lifshitz), pada akhirnya ia menulis disertasi tentang topik yang ditunjuk oleh kuratornya - fisika partikel dan penilaian kelas diagram Feynman untuk menghamburkan foton oleh partikel skalar. . Disertasi itu tidak terlalu menarik, tetapi pada tahun 1970 ia dikirim ke Cornell University sebagai postdoc.

Mitchell mulai memiliki masalah dengan motivasi, dan bukannya melakukan fisika, ia lebih suka menghabiskan waktu di kafe, menyelesaikan teka-teki silang di New York Times (yang berhasil ia lakukan dengan sangat cepat). Tetapi di Cornell, Mitchell mendapat beberapa teman penting. Salah satunya adalah Predrag Tsvitanovic, seorang mahasiswa pascasarjana yang luar biasa dari bagian Yugoslavia yang sekarang disebut Kroasia; ia belajar elektrodinamika kuantum, dan berbagi minat dengan Mitchell dalam sastra Jerman. Lain adalah penyair muda Kathleen Durish (yang kemudian menjadi Katie Hammond), seorang teman Predrag. Yang lainnya adalah bintang fisika yang sedang naik daun, Profesor Pete Carruthers, yang berbagi minat dengan Mitchell dalam musik klasik.

Pada awal 1970-an, zaman keemasan teori medan kuantum semakin dekat. Tetapi, terlepas dari tema karyanya, Mitchell tidak melakukan ini, dan setelah dua tahun di Cornell tidak membuahkan hasil. Namun, ia berhasil mengesankan Hans Bethe , dan ia memindahkannya ke tempat lain, juga sebagai postdoc, tetapi ke sebuah lembaga yang menempati tempat yang sedikit lebih rendah dalam hierarki tidak resmi - Politeknik Virginia.

Di Virgin Institute, Mitchell bahkan lebih sedikit daripada di Cornell. Dia praktis tidak berkomunikasi dengan orang-orang, dan hanya memberikan satu karya di tiga halaman: "Hubungan koefisien normalisasi dan fungsi dispersi dalam persamaan transportasi multigroup". Sesuai namanya, karya itu teknis dan tidak menarik.

Pada akhir masa tinggal dua tahun Mitchell di Virginia, tidak jelas apa yang akan terjadi selanjutnya. Namun, keberuntungan ikut campur. Teman Mitchell dari Cornell, Pete Carruthers, disewa untuk mendirikan unit teoretis di Los Alamos, dan diberi carte blanche untuk mempekerjakan beberapa fisikawan muda terkemuka. Pete kemudian dengan bangga mengatakan kepada saya (sebagai bagian dari saran manajemen ilmiah) bahwa ia merasa bahwa Mitchell mampu melakukan sesuatu yang hebat, dan, terlepas dari pendapat orang lain - dan bukti - ia memutuskan untuk mengenakannya.

Setelah mentransfer Mitchell ke Los Alamos, Pete mulai menawarkan kepadanya proyek. Pada awalnya itu adalah kelanjutan dari karya Pete, upaya untuk menghitung sekelompok sifat kolektif ("transportasi") dari teori medan kuantum untuk memahami tabrakan partikel berenergi tinggi - ini adalah karya yang mendahului studi plasma quark-gluon.

Namun segera, Pete menyarankan agar Mitchell menangani turbulensi cairan, khususnya, untuk mengetahui apakah metode kelompok renormalisasi akan membantu dalam masalah ini.

Ketika cairan - misalnya, air - mulai mengalir cukup cepat, pusaran air kecil muncul di dalamnya, dan mulai berperilaku dalam kompleks, dan, pada pandangan pertama, secara acak. Tetapi meskipun fenomena ini telah dibahas secara kualitatif selama berabad-abad (misalnya, bahkan Leonardo da Vinci membuat sketsa-sketsa), fisikawan dapat mengatakan tentang hal itu sangat sedikit - meskipun pada tahun 1940-an Andrei Nikolaevich Kolmogorov membuat pernyataan bahwa pusaran air harus membentuk kaskade dengan k - distribusi energi. Di Los Alamos, para ilmuwan fokus pada pengembangan senjata atom (yang mau tidak mau melibatkan mempelajari perilaku cairan dengan arus kuat), dan turbulensi sangat penting untuk dipahami - meskipun tidak jelas bagaimana cara mendekatinya.

Pada 1974, muncul berita bahwa Kenneth Wilson dari Cornell "menyelesaikan masalah Kondo" [masalah Kondo adalah ketidakmampuan fisika teoretis untuk menjelaskan efek Kondo / kira-kira. trans.] menggunakan teknik yang disebut "kelompok renormalisasi." Pete Carruthers menyarankan Mitchell menerapkan teknik ini untuk turbulensi.

Grup renormalisasi terkait dengan bagaimana mengubah skala (atau parameter lain) memengaruhi deskripsi (dan perilaku) sistem. Kebetulan bahwa PhD Mitchell dari MIT, Francis Lowe, bersama dengan Murray Gel-Mann, memperkenalkannya kembali pada tahun 1954 dalam konteks elektrodinamika kuantum. Gagasan itu tidak bergerak selama bertahun-tahun, tetapi kembali pada tahun 1970-an dan secara aktif diterapkan - meskipun dengan cara yang berbeda - pada fisika partikel (terutama kromodinamika kuantum ) dan fisika benda terkondensasi.

Dalam sepotong besi di dalam ruangan, Anda dapat menyelaraskan putaran semua elektron yang terkait dengan masing-masing atom, dan kemudian besi akan bermagnet. Tetapi jika Anda menghangatkan setrika, fluktuasi mulai di dalamnya, dan tiba-tiba - pada suhu di atas yang disebut. Poin curie (770 ° C untuk besi) - begitu banyak keacakan muncul dalam besi sehingga sifat magnetiknya hilang. Secara umum, ada beberapa situasi (mencair, mendidih, pembentukan kemacetan lalu lintas) ketika tiba-tiba ini disebut transisi fase .

Tetapi apa yang sebenarnya terjadi selama fase transisi? Saya pikir cara termudah untuk melihat ini adalah dengan mempelajari rekannya di bidang automata seluler. Dengan aturan tertentu, yang diberikan di bawah ini, ketika sistem awalnya tidak memiliki sejumlah besar sel hitam, segera semua akan berubah menjadi putih. Tetapi jika Anda meningkatkan jumlah sel hitam asli (dengan analogi dengan meningkatkan suhu sistem magnetik), maka tiba-tiba, dalam kasus ini, dengan proporsi 50% sel hitam, transisi yang tajam terjadi, dan seluruh sistem akhirnya berubah menjadi hitam (pengamatan bagi para ahli tentang transisi fase: ya , ini adalah fase transisi dalam sistem satu dimensi; dua dimensi hanya bisa diperlukan jika sistem perlu dibalik secara mikroskopis ).



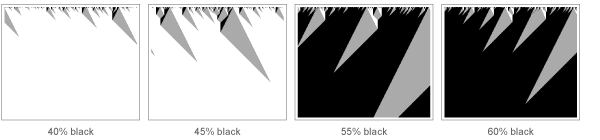
Tetapi apa yang terjadi pada sistem di dekat perbatasan 50% sel hitam? Bahkan, dia tidak bisa memutuskan apakah akan menjadi hitam atau putih. Hasilnya, ia menunjukkan seluruh hierarki fluktuasi, dari yang terkecil hingga yang terbesar. Pada 1960-an, menjadi jelas bahwa "eksponen kritis" yang mengkarakterisasi undang-undang kekuasaan yang menggambarkan fluktuasi ini adalah sama untuk banyak sistem.

Tetapi bagaimana kita menghitung eksponen kritis ini? Dalam beberapa kasus buatan, metode analitis diketahui. Tetapi sebagian besar, sesuatu yang lain diperlukan.Pada akhir 1960-an, Ken Wilson menyadari bahwa kelompok renormalisasi dan komputer dapat digunakan. Dimungkinkan untuk membuat model untuk interaksi masing-masing putaran. Tetapi kelompok renormalisasi memberi Anda prosedur "penskalaan" untuk interaksi blok berputar yang lebih besar. Dan dengan mempelajari ini di komputer, Ken Wilson berhasil mulai menghitung eksponen kritis.

Pada awalnya, fisikawan tidak memperhatikan hal ini, paling tidak karena mereka tidak terbiasa menggunakan komputer secara aktif dalam fisika teoretis. Tapi kemudian masalah Kondo muncul. Pada sebagian besar material, hambatan listrik berkurang dengan menurunnya suhu (dan pada superkonduktor berkurang menjadi nol bahkan pada suhu yang lebih besar dari nol absolut). Namun, pada 1930-an, pengukuran pada emas menunjukkan bahwa daya tahannya meningkat pada suhu rendah. Pada 1960-an, diyakini bahwa semuanya adalah hamburan elektron oleh pengotor magnetik - namun, kalkulasi mengalami masalah, memberikan hasil yang tak terbatas.

Kemudian pada tahun 1975, Ken Wilson menerapkan metode kelompok renormalisasi - dan dapat secara akurat menghitung efeknya. Efek ini masih diselimuti beberapa misteri (mungkin karena fakta bahwa saya sering kesulitan memahami penjelasan Ken Wilson tentang topik ini, setidaknya sejak saya bertemu dengannya di tahun 1980-an). Tetapi gagasan bahwa kelompok renormalisasi mungkin penting telah mengakar.

Bagaimana itu bisa diterapkan pada turbulensi fluida? Hukum kekuasaan Kolmogorov memberikan ide-ide tertentu. Tetapi apakah mungkin untuk mengambil persamaan Navier-Stokes yang mengontrol aliran cairan yang diidealkan dan mendapatkan salah satu dari mereka? Proyek ini diambil oleh Mitchell Feigenbaum.

Penemuan besar

Persamaan Navier-Stokes sangat sulit untuk dikerjakan. Sampai hari ini tidak begitu jelas bagaimana bahkan sifat turbulensi yang paling jelas - keacakan yang tampak - muncul dari mereka. Mungkin persamaan ini bukan deskripsi matematis yang lengkap atau konsisten, dan kita benar-benar melihat peningkatan gerakan mikroskopis dari molekul. Mungkin - seperti dalam teori chaos dan persamaan Lorentz - semuanya adalah untuk meningkatkan keacakan dalam kondisi awal. Secara pribadi, berdasarkan pekerjaan saya dari tahun 1980-an, saya percaya bahwa intinya adalah dalam sifat-sifat perhitungan internal mereka, mirip dengan keacakan dalam " aturan 30 " saya untuk otomat seluler.

Bagaimana Mitchell mendekati masalah ini? Dia mencoba menyederhanakannya - pertama dengan bergerak dari persamaan yang bergantung pada ruang dan waktu ke persamaan yang hanya bergantung pada waktu, dan kemudian membuatnya terpisah dan mempelajari pemetaan iteratif. Dari Paul Stein, Mitchell mengetahui pekerjaan sebelumnya tentang pemetaan berulang yang dilakukan di Los Alamos (yang tidak banyak diketahui). Tetapi Mitchell tidak mengerti ke mana harus melanjutkan, meskipun, setelah menerima di tangannya, sebuah kalkulator baru yang dapat diprogram ultra-modern, HP-65, ia memutuskan untuk memprogram tampilan berulang di atasnya.

Kemudian, pada Juli 1975, Mitchell pergi ke pertemuan fisik musim panas di Aspen, Colorado. Di sana dia bertemu dengan Stephen Smale, seorang ahli matematika terkenal yang mempelajari sistem dinamis, dan terkejut mengetahui bahwa dia berbicara tentang pemetaan iteratif. Smale disebutkan seseorang yang meminta mungkin untuk mengekspresikan periode batas menggandakan kaskade dengan _∞ ≈ 3,56995 melalui tipe standar konstanta π dan √2. Smale tidak tahu jawaban untuk pertanyaan ini. Namun, Mitchell menjadi tertarik pada ini, dan memutuskan untuk mencoba mencari tahu jawabannya.

Dia tidak memiliki HP-65 bersamanya, tetapi dia terjun ke masalah ini menggunakan alat standar dari seorang ahli fisika matematika berpendidikan, dan segera mengubah tugas menjadi pencarian fungsi kutub pada bidang kompleks, yang tidak ada yang dia katakan. Namun, kembali ke Los Alamos pada bulan Agustus, ia beralih ke HP-65-nya, dan mulai memprogramnya untuk mendeteksi titik bifurkasi _dan .

Untuk n kecil, iterasi berjalan cukup cepat. Untuk n = 5, butuh 30 detik. Untuk n = 6, saya harus menunggu beberapa menit. Namun, ketika kalkulator bekerja, Mitchell memutuskan untuk melihat nilai-nilai _dan yang sudah dia miliki, dan memperhatikan sesuatu: mereka tampaknya secara geometris berusaha untuk mendapatkan nilai akhir.

Pada awalnya, ia hanya menggunakan fakta ini untuk memperkirakan _∞ , yang, meskipun telah berusaha keras, ia tidak dapat mengungkapkannya melalui konstanta standar. Tetapi ia segera mulai curiga bahwa eksponen konvergensi δ lebih penting daripada _∞ - karena nilainya tetap tidak berubah dengan perubahan sederhana pada variabel-variabel di peta. Selama sekitar satu bulan, Mitchell mencoba mengekspresikan δ dalam hal konstanta standar.

Tetapi kemudian, pada Oktober 1975, ia ingat bahwa Paul Stein mengatakan bahwa menggandakan periode tampak tidak hanya sama untuk pemetaan logistik, tetapi umumnya untuk semua pemetaan iteratif dengan satu maksimum. Setelah bersatu kembali dengan HP-65 setelah melakukan perjalanan ke Caltech, Mitchell segera mencoba tampilan x → sin (x) dan menemukan bahwa, dengan hingga tiga tempat desimal, eksponen δ persis sama.

Dia segera memutuskan bahwa dia telah menemukan sesuatu yang indah. Tetapi Stein mengatakan dia akan membutuhkan lebih banyak angka untuk menarik kesimpulan. Ada banyak komputer yang kuat di Los Alamos, jadi hari berikutnya Mitchell meminta seseorang untuk menunjukkan kepadanya bagaimana menulis program FORTRAN untuk melanjutkan - dan pada akhir hari ia dapat menghitung bahwa dalam kedua kasus δ memiliki nilai sekitar 4,6692 .

Komputer yang ia gunakan adalah tipuan pekerja keras untuk sains AS pada masa itu: model CDC 6000 (jenis yang sama yang saya gunakan ketika saya pertama kali pindah ke AS pada tahun 1978). Ini dikembangkan oleh Seymour Cray, dan secara default ia menggunakan angka floating point 60-bit. Tetapi dengan akurasi seperti itu (14 digit setelah titik desimal) Mitchell tidak bisa mendapatkan yang lebih baik dari 4,6692. Untungnya, istri Pete, Lucy Carruthers, adalah seorang programmer Los Alamos, dan dia menunjukkan kepada Mitchell cara menggunakan presisi ganda. Hasilnya, ia dapat menghitung δ hingga 11 tempat desimal, dan menentukan bahwa nilai dari dua pemetaan iteratif yang berbeda adalah sama.

Selama beberapa minggu, Mitchell menemukan bahwa δ tampaknya menjadi nilai universal untuk semua peta iterasi dengan satu kuadrat maksimal. Tetapi dia tidak tahu mengapa ini terjadi, dan dia tidak memiliki alat matematika khusus untuk mempelajari masalah ini. Tetapi pada akhirnya, pada usia 30, Mitchell menemukan sesuatu yang tampak sangat menarik baginya.

Pada hari ulang tahunnya pada 19 Desember, Mitchell bertemu dengan temannya Predrag dan memberi tahu dia tentang hasil ini. Namun, pada saat itu, Predrag bekerja dengan fisika partikel utama, dan dia tidak mementingkan hal ini.

Mitchell terus bekerja, dan setelah beberapa bulan dia menjadi yakin bahwa tidak hanya eksponen δ yang universal - dengan skala yang tepat, pemetaan iteratif sendiri juga universal. Pada April 1976, Mitchell menulis laporan tentang temuannya. Pada 2 Mei 1976, dia berbicara tentang mereka dalam sebuah kuliah di Advanced Research Institute di Princeton. Predrag ada di sana, dan akhirnya dia tertarik pada karya Mitchell.

Tapi Predrag cukup sering tidak jelas apa yang dibicarakan Mitchell. Tetapi hari berikutnya, Predrag berhasil berhasil menyederhanakan tugas dan mendapatkan satu persamaan fungsional langsung untuk bentuk terbatas dari peta iterasi berskala: g (g (x)) = -g (α x) / α, di mana α ≈ 2.50290, yang menyiratkan bahwa untuk setiap pemetaan berulang jenis tertentu, bentuk terbatasnya akan terlihat seperti versi yang lebih berliku-liku dari pemetaan ini:

Bagaimana semuanya berkembang

Bidang penelitian tentang pemetaan berulang mendapatkan momentum pada 10 Juni 1976 setelah menerbitkan ulasan dalam jurnal Nature oleh Robert May, yang ia tulis secara independen dari Mitchell, dan, tentu saja, tanpa menyebutkan hasil yang ia peroleh. Tetapi dalam bulan-bulan berikutnya, Mitchell bepergian dengan laporannya tentang hasilnya. Reaksi mereka beragam. Fisikawan tertarik pada bagaimana hasil ini berhubungan dengan fisika. Matematikawan tidak memahami status mereka, mengingat bahwa mereka diperoleh dari matematika eksperimental dan tidak memiliki bukti matematika formal. Dan, seperti biasa, sulit bagi orang untuk memahami penjelasan Mitchell.

Pada musim gugur 1976, Predrag mendapat postdoc di Oxford, dan pada hari pertama saya tiba di sana, seorang siswa berusia 17 tahun yang menulis diploma fisika partikel, saya bertemu dengannya. Kami terutama berbicara tentang metode “jejak burung” yang elegan untuk bekerja dengan teori grup (buku yang akhirnya diterbitkan 32 tahun kemudian). Dia juga mencoba menjelaskan peta iteratif kepada saya. Dan saya masih ingat bagaimana dia berbicara tentang model populasi ikan ideal di Laut Adriatik (hanya setelah bertahun-tahun saya menghubungkan ini dengan fakta bahwa Predrag berasal dari tempat-tempat yang sekarang disebut Kroasia).

Pada waktu itu saya tidak mementingkan hal ini, tetapi gagasan pemetaan berulang menjadi tertanam dalam pikiran saya, dan segera bercampur dengan gagasan fraktal, yang saya pelajari dari buku Benoit Mandelbrot . Dan ketika, setelah beberapa tahun, saya fokus pada masalah kompleksitas, ide-ide ini membantu saya datang ke sistem seperti automata seluler.

Tetapi pada tahun 1976, Mitchell (sampai pertemuan saya berikutnya dengan siapa beberapa tahun lagi akan berlalu) aktif bepergian dengan laporan hasil. Dia juga menyerahkan karya ke jurnal ilmiah bergengsi Kemajuan dalam Matematika. Selama enam bulan dia tidak menerima berita dari sana, tetapi pada akhirnya pekerjaan itu ditolak. Dia mencoba lagi, mengirim pekerjaan lain ke SIAM Journal of Applied Mathematics - dengan hasil yang sama.

Saya ingin mengatakan bahwa saya tidak terkejut dengan ini. Dalam pengalaman saya tentang publikasi dalam literatur akademis (yang sudah lama tidak saya lakukan), menerbitkan karya dalam bidang penelitian yang didefinisikan cukup mudah. Tetapi bekerja di bidang sesuatu yang benar-benar baru atau asli dapat secara praktis bergantung pada penolakan setelah penilaian ahli - baik karena kepicikan intelektual atau karena korupsi akademik. Mitchell punya masalah lain - penjelasannya sulit dimengerti.

Tetapi akhirnya, pada tahun 1977, Joel Lebovitz, editor Journal of Statistical Physics, setuju untuk menerbitkan karya Mitchell - pada kenyataannya, karena dia bertemu dengannya, karena dia mengakui bahwa dia tidak memahami pekerjaan itu. Maka karya 1978 “Universalitas Kuantitatif di Kelas Transformasi Nonlinier” muncul, menggambarkan pencapaian hebat Mitchell. Untuk menetapkan prioritas akademik, Mitchell kadang-kadang mengutip ringkasan dari laporan yang ia buat pada tanggal 26 Agustus 1976, dan diterbitkan dalam koleksi tahunan Divisi Teoritis Los Alamos untuk laporan tahunan 1975-1976. Mitchell sangat dipengaruhi oleh penolakan untuk menerbitkan karya-karyanya, dan selama bertahun-tahun ia menyimpan surat-surat dengan penolakan di laci.

Mitchell terus melakukan perjalanan keliling dunia dengan laporan hasil. Ada minat pada mereka, tetapi ada kebingungan. Namun, sesuatu yang menakjubkan terjadi pada musim panas 1979: Albert Liebhaber dari Paris melaporkan hasil percobaan fisik pada transisi menuju turbulensi dalam aliran konvektif helium cair, di mana ia melihat penggandaan periode persis dengan eksponen δ yang dihitung Mitchell. Ternyata menjadi universal tidak hanya untuk kelas sistem matematika, tetapi juga terbukti nyata, sistem fisik.

Dan seketika Mitchell menjadi terkenal. Koneksi dengan kelompok renormalisasi ditemukan, karyanya menjadi modis untuk fisikawan dan matematikawan. Mitchell terus naik dengan laporan, tetapi sekarang ia memiliki kesempatan untuk secara teratur bergaul dengan fisikawan dan ahli matematika terbaik.

Saya ingat bagaimana dia datang ke Caltech, sekitar musim gugur 1979. Semua ini menyerupai pertemuan dengan bintang rock. Mitchell tiba, membuat laporan penuh gaya, tetapi sedikit misterius, dan kemudian Richard Feynman dan Murray Gell-Man mencurinya untuk percakapan pribadi.

Segera, Mitchell ditawari banyak pekerjaan kelas atas yang berbeda, dan pada tahun 1982 ia kembali dengan kemenangan ke Caltech sebagai profesor fisika. Ada pembicaraan bahwa penemuan itu layak mendapatkan hadiah Nobel, dan pada Juni 1984 ia muncul di majalah New York Times, dengan Beethoven yang anggun, di tengah air terjun Cornell:



Tapi matematikawan tetap tidak senang. Seperti dalam kasus Benoit Mandelbrot, mereka menganggap hasil Mitchell sebagai "hipotesis numerik", tidak terbukti, dan tidak layak disebutkan. Namun, ahli matematika terbaik (dengan siapa Mitchell berteman) segera mulai bekerja pada masalah ini, dan hasilnya tidak lama datang - meskipun butuh sepuluh tahun untuk menyelesaikan dan bukti akhir dari universalitas δ.

Kemana perginya ilmu pengetahuan?

Apa yang terjadi dengan penemuan besar Mitchell? Itu, tentu saja, menjadi terkenal. Dan kaskade dengan periode penggandaan dengan sifat universal segera ditemukan di sejumlah sistem - dalam cairan, optik, dll. Tapi seberapa umum mereka? Bisakah mereka diperluas untuk mencakup seluruh masalah turbulensi dalam fluida?

Mitchell dan yang lainnya mempelajari sistem selain pemetaan iteratif dan menemukan fenomena terkait. Tetapi di antara mereka tidak mengejutkan seperti penemuan pertama Mitchell.

Dalam arti tertentu, upaya saya untuk mempelajari automata seluler dan perilaku program-program sederhana, yang dimulai pada tahun 1981, ditujukan untuk mencari beberapa pertanyaan besar yang dapat dituntun oleh pekerjaan Mitchell. Namun, metode dan hasil kami sangat berbeda. Mitchell selalu berusaha untuk tetap dekat dengan hal-hal yang dapat ditelusuri oleh fisikawan matematika tradisional, dan saya tanpa rasa takut masuk ke dunia komputasi, menjelajahi fenomena yang ditemukan di sana.

Saya mencoba memahami bagaimana pekerjaan Mitchell dapat dikaitkan dengan pekerjaan saya, dan dalam pekerjaan pertama saya di automata seluler pada tahun 1981, saya bahkan mencatat, misalnya, bahwa kepadatan rata-rata sel hitam dalam langkah-langkah berturut-turut dalam evolusi otomat seluler dapat diperkirakan kira-kira melalui pemetaan berulang.

Saya juga mencatat bahwa secara matematis seluruh evolusi otomat seluler dapat dianggap sebagai peta iteratif - meskipun tidak pada himpunan bilangan real biasa, tetapi pada himpunan cantor . Dalam karya pertama saya, saya bahkan membangun analogi pemetaan Mitchell yang halus, namun, semuanya liar dan terputus-putus dalam diri saya:



Tetapi, tidak peduli bagaimana saya mencoba, saya tidak dapat menemukan hubungan yang jelas dengan karya Mitchell. Saya sedang mencari analog dari penggandaan periode atau perintah Sharkovsky , tetapi saya tidak menemukan sesuatu yang istimewa. Untuk platform komputasi saya, bahkan berpikir tentang bilangan real dengan urutan angka tak terbatas mereka tidak wajar. Bertahun-tahun kemudian, dalam buku "A New Kind of Science", saya memasukkan catatan "Smooth Iterative Mapping". Saya menunjukkan urutan angka-angka mereka dan mengamati bagaimana penemuan Mitchell menyiratkan adanya struktur bersarang yang tidak biasa pada awal urutan:

Akhir cerita

Apa yang terjadi pada Mitchell? Setelah menghabiskan empat tahun di Cornell, ia pindah ke Universitas Rockefeller di New York, dan 30 tahun berikutnya menjalani kehidupan yang hampir bohemian, menghabiskan sebagian besar waktunya di apartemennya di Upper East Side di Manhattan.

Ketika berada di Los Alamos, Mitchell menikahi seorang wanita keturunan Jerman bernama Cornelia, saudara fisikawan (dan teman lama saya) David Campbell, yang mendirikan Pusat Studi Nonlinier di Los Alamos, dan kemudian menjadi rektor Universitas Boston. Namun, agak cepat, Cornelia meninggalkan Mitchell, dan tidak lain dari Pete Carruthers. Belakangan, Pete, yang menderita kecanduan alkohol dan masalah-masalah lain, bersatu kembali dengan istrinya Lucy, tetapi meninggal pada tahun 1997 pada usia 61 tahun.

Di Cornell, Mitchell bertemu Gunilla, yang, pada usia 14, melarikan diri dari keluarga pendeta dari sebuah kota kecil di Swedia utara, dan pada awalnya adalah model dengan Salvador Dali, dan kemudian datang ke New York sebagai model mode pada tahun 1966. Gunilla adalah seorang jurnalis, direkam dalam video, menulis drama dan melukis gambar. Mereka menikahi Mitchell pada tahun 1986, dan pernikahan mereka berlangsung selama 26 tahun, di mana Gunilla membuat karir yang baik dalam seni figuratif .

Karya terbaru, yang ditulis oleh Mitchell sendiri, diterbitkan pada tahun 1987. Dia juga menerbitkan banyak karya dengan berbagai penulis bersama, meskipun tidak satu pun yang menjadi sangat penting. Sebagian besar dari mereka melanjutkan penelitian awalnya, atau mencoba menerapkan metode tradisional fisika matematika untuk berbagai fenomena kompleks yang mirip dengan aliran fluida.

Mitchell suka berinteraksi dengan eselon atas akademisi. Dia menerima segala macam penghargaan dan pengakuan (kecuali untuk Hadiah Nobel). Tetapi sampai akhir dia menganggap dirinya orang luar - seorang pria Renaisans yang fokus pada fisika, tetapi tidak sepenuhnya percaya pada semua institusi dan praktik.

Sejak awal 1980-an, saya sering bertemu dengan Mitchell, di New York dan di tempat lain. Dia menggunakan platform Mathematica setiap hari, memujinya, dan sering berbicara tentang perhitungan rumit yang dia lakukan dengannya. Seperti banyak fisikawan matematika, Mitchell adalah seorang ahli dalam fungsi-fungsi khusus, dan sering berbicara dengan saya tentang fungsi yang semakin eksotis, yang, menurut pendapatnya, harus kita tambahkan ke produk.

Mitchell memiliki dua hobi utama di luar bidang akademik. Pada pertengahan 1980-an, penyair muda, yang sekarang bernama Katie Hammond, dan yang dikenal Mitchell dari Cornell, adalah seorang manajer periklanan untuk New York Times, dan menikahi seorang lelaki dari keluarga yang memiliki Hammond World Atlas Publishing House. Melalui itu, Mitchell terjun ke dunia kartografi yang sama sekali baru.

Saya berbicara dengannya tentang topik ini berkali-kali. Dia bangga telah menemukan cara menggunakan teorema pemetaan Riemann untuk mendapatkan pemetaan lokal khusus saat membuat peta. Dia menjelaskan kepada saya sebuah algoritma berbasis fisika untuk menempatkan label pada peta (walaupun saya masih belum sepenuhnya memahaminya). Dia sangat senang dengan rilis edisi baru atlas Hammond (yang kemudian dia sebut "atlas saya").

Sejak 1980-an, tren penerapan gagasan fisik pada keuangan kuantitatif telah berkembang secara aktif, dan fisikawan sering menjadi analis Wall Street. Dan karena pemodal terus mencari manfaat unik, selalu ada minat dalam metode baru. Saya sering dihubungi dengan pertanyaan serupa - tetapi setelah keberhasilan buku James Gleick 1987 "Chaos" (tentang yang saya berikan wawancara panjang), banyak orang muncul yang ingin tahu bagaimana "kekacauan" dapat membantu mereka mengelola keuangan mereka.

Salah satunya adalah seseorang Michael Gudkin . Belajar di perguruan tinggi pada awal 1960-an, Ia mendirikan perusahaan riset hukum untuk mahasiswa hukum. Beberapa tahun kemudian, ia mempekerjakan beberapa ekonom yang memenangkan Hadiah Nobel, dan mendirikan, mungkin, dana lindung nilai pertama untuk berurusan dengan perdagangan arbitrase menggunakan komputer. Gudkin adalah moto seumur hidupnya, ia suka judi, bepergian dan backgammon, dan menghasilkan banyak uang. Pada salah satu momen malang, dia mencari beberapa solusi baru - dan menemukan teori chaos dan Mitchell Feigenbaum.

Dia bekerja pada berbagai fisikawan selama beberapa tahun, dan kemudian pada 1995 dia membentuk sebuah tim dan mendirikan perusahaan Numerix untuk mengkomersilkan penggunaan metode perhitungan fisik dalam bidang instrumen keuangan yang semakin eksotis. Mitchell Feigenbaum adalah wajah perusahaan, meskipun teman lama saya Nigel Goldenfield dan rekan mudanya Sasha Sokol melakukan semua kerja keras.

Sejak awal, perusahaan memiliki banyak pekerjaan yang berkaitan dengan fisika matematika, dan Mitchell berpartisipasi aktif di dalamnya. Dia adalah pencinta hebat kalkulus stokastik Ito, menguliahinya dan bangga telah menemukan metode mempercepat integrasi stokastik seribu kali lipat. Namun, perusahaan sebenarnya menulis perpustakaan di C ++ untuk diintegrasikan ke dalam sistem bank. Mitchell tidak ingin melakukan hal seperti ini dalam jangka panjang. Setelah beberapa tahun bekerja, aktivitasnya di perusahaan menurun.

Saya bertemu dengan Gudkin pada tahun 1998, dan kemudian 14 tahun kemudian. Tidak lama sebelum itu, ia menulis otobiografi, "Jawaban yang Salah untuk Menjadi Lebih Cepat: Sejarah Rahasia Menciptakan Mesin Triliun-Perdagangan," dan ia tiba-tiba menghubungi saya, menawarkan diri untuk berpartisipasi dalam bisnis baru yang tidak jelas. Mitchell masih berbicara dengan baik tentang Michael, meskipun ketika percakapan tiba-tiba terjadi bahwa saya mendirikan perusahaan baru dan menjadi direkturnya, saya menolak.

Bertahun-tahun ini, saya cukup sering berbicara dengan Mitchell, meskipun kontak kami tidak terpelihara dengan baik dalam arsip, karena ia lebih suka berbicara lebih banyak melalui suara daripada melalui surat. Dia pernah menulis kepada saya: “Saya tidak suka berkorespondensi melalui email. Saya masih lebih suka mendengar suara dan berinteraksi dengan orang itu. "

Tetapi beberapa fragmen disimpan dalam arsip saya. Misalnya, ada korespondensi berkenaan dengan ulang tahun Mitchell yang ke-60 pada tahun 2004, yang tidak saya dapatkan, karena bersinggungan dengan ulang tahun salah satu anak saya. Sebagai gantinya, saya memerintahkan produksi Feigenbaum-Zvitanovich Crystal, patung kaca tiga dimensi yang menggambarkan pembatasan fungsi g (z) pada bidang kompleks.

Memecahkan persamaan fungsional agak sulit, dan ukiran laser pertama membelah beberapa blok kaca, tetapi pada akhirnya objek ini dibuat dan dikirim - dan bertahun-tahun kemudian saya senang melihatnya di rak di apartemen Mitchell:



Kadang-kadang, dalam arsip saya, disebutkan tentang Mitchell yang muncul oleh orang lain, biasanya oleh Predrag. Pada 2007, Predrag menulis kepada saya (dengan selera humornya yang khas):

Untuk berita lain: baru saja bertemu Mitchell, dia bertemu dengan Odyssey.

Maksud saya bukan layanan pengawalan yang mahal, tetapi Homer's Odyssey. Dia mengambil menghitung lokasi bintang sebagai fungsi dengan presesi 26.000 tahun. Dia mengatakan bahwa Hipparchus pernah menghitung semua ini, tetapi Gereja Katolik berhasil menghancurkan semua salinan tablet-tabletnya. "

Membenarkan citranya sebagai pria Renaisans, Mitchell selalu serius tertarik pada sejarah. Pada 2013, sebagai tanggapan terhadap artikel saya tentang Leibniz, Mitchell mengatakan bahwa dia telah menjadi kekasih Leibniz sejak remaja, dan menjelaskan:

" Hagiografer Newton, Voltaire, tidak tahu tentang esensi monadologi , jadi saya hanya bisa memalsukan" yang terbaik dari semua dunia yang mungkin. "Suatu ketika saya menerbitkan ini sebagai cara lisan untuk menjelaskan universalitas 2 ⁿ .

Yang kedua dari karya Leibniz, diterbitkan ketika ia berusia 19 tahun, "On Tangent Inversion Methods," atau sesuatu seperti itu, berisi penemuan metode isocline untuk menyelesaikan persamaan diferensial biasa. Leibniz dan Newton mulai dengan persamaan diferensial, setelah menerima notasi diferensial. Kisah yang sangat menarik. "

Namun, fisika matematika selalu menjadi benteng kehidupan intelektual Mitchell, meskipun lebih pada tingkat pribadi daripada sebagai bagian dari pekerjaan akademisnya. Pada suatu saat, anak baptisnya, yang masih sangat muda, bertanya kepadanya mengapa bulan, yang lebih dekat ke cakrawala, tampaknya lebih besar. Dia menulis jawabannya (sedikit seperti surat Euler kepada seorang puteri Jerman), dan kemudian menyadari bahwa dia tidak yakin dengan jawabannya, dan memulai penelitian bertahun-tahun dalam bidang optik dan pencitraan. Begitu sampai di MIT, ia menjadi tertarik pada karya retina, yang diilhami oleh buku Jerry Lettwin "Apa yang Dikatakan Mata Katak kepada Otak Katak".

Dia mengatakan kepada saya tentang ini, mengatakan bahwa teori pembentukan citra yang biasa adalah salah, dan bahwa dia memiliki teori yang lebih baik. Dia selalu menggunakan ukuran bulan sebagai contoh, tetapi saya tidak yakin apakah masalah ini terkait dengan optik atau persepsi. Dia tidak pernah menerbitkan karya-karya yang berhubungan dengan topik ini, walaupun dengan sedikit keberuntungan manuskripnya (menurut rumor, dia sedang menyiapkan buku), sebagai akibatnya mereka akan melihat cahaya - jika ada orang lain yang bisa memahaminya.

Ketika saya mengunjungi Mitchell dan Gunilla, apartemen mereka membuat kesan bohemian - di mana-mana ada buku, kertas, lukisan, dan berbagai hal serupa. Dan ada seekor burung. Itu adalah kakatua, dan itu keras. Saya tidak tahu siapa dan mengapa membawanya. Tapi dia cukup merepotkan. Mitchell dan Gunilla hampir diusir dari apartemen karena keluhan tetangga tentang kebisingan, dan mereka akhirnya mengantar Burung ke dokter. Seperti yang kemudian saya ketahui, secara tak terduga meninjau rencana yang tidak pernah diterapkan untuk mengembangkan video game untuk hewan peliharaan ("pikiran orang lain tentang planet kita"), kakaktua adalah makhluk sosial, dan hewan peliharaan semacam itu pasti membutuhkan "twitter untuk kakaktua."



Akibatnya, Gunilla meninggalkan keluarga, dan, menurut rumor, itu karena Burung.

Terakhir kali kami bertemu dengan Mitchell secara langsung beberapa tahun yang lalu. Anak saya, Christopher, dan saya datang mengunjunginya - dan dia bersemangat seperti Mitchell, matanya berbinar-binar, dia berbicara dengan cepat dan sedikit misterius tentang masalah fisika matematika pembentukan gambar. "Mata burung-burung itu berlebihan," katanya pada suara kakatua dari kamar sebelah. Fossa pusat mereka sangat kecil. Mata mereka bekerja seperti teleskop. "

"Mata ikan adalah yang terbaik," katanya, menjelaskan bahwa semua mata muncul sebagai hasil evolusi di bawah air - dan arsitektur mereka tidak banyak berubah sejak saat itu. "Ikan menjaga seluruh bidang pandang tetap fokus, tidak seperti kita," katanya. Itu menawan, eksentrik, dan sangat Mitchell.

Selama bertahun-tahun, kami secara berkala berbicara di telepon, biasanya menjelang malam. Beberapa bulan yang lalu saya bertemu Predrag, dan mengatakan kepadanya bahwa saya terkejut bahwa saya sudah lama tidak berbicara dengan Mitchell. Dia menjelaskan bahwa Mitchell sakit, tetapi tidak memberi tahu siapa pun tentang hal itu. Beberapa minggu yang lalu, sekitar tengah malam, Predrag mengirimi saya email dengan subjek "Mitchell sudah mati," menjelaskan bahwa Mitchell meninggal sekitar pukul 8 malam dan melampirkan foto khas "Mitchell di New York" ke surat itu:



Selama bertahun-tahun, saya telah mengembangkan ritual tertentu untuk diri saya sendiri - ketika saya mendengar tentang kematian seorang teman, saya segera mulai mencarinya di arsip saya. Dan saya tiba-tiba menemukan bahwa beberapa tahun yang lalu Mitchell menelepon voicemail saya, keberadaan yang saya tidak curigai. Jadi sekarang saya bisa memberi Mitchell kesempatan untuk mengucapkan kata terakhir .

Dan, tentu saja, tulis nomor terakhir: 4.66920160910299067185320382 ...