👃🏽 👨‍👨‍👧‍👦 ✊🏽 Fluktuasi kosmologi dan kuantum di browser 🌇 😳 🃏

Mari kita menetapkan tujuan yang murni praktis - untuk menerapkan kanvas tanpa akhir dengan kemampuan untuk bergerak dan skala dengan mouse. Kanvas semacam itu, misalnya, dapat berfungsi sebagai sistem koordinat bergerak dalam editor grafis. Implementasi ide kami tidak begitu rumit, tetapi proses pemahaman itu terkait dengan objek-objek matematika dan fisik yang mendasar, yang akan kita pertimbangkan saat kita kembangkan.

Hasil

Pernyataan masalah

Dari kanvas kami, kami hanya ingin melakukan dua fungsi: menggerakkan mouse dan pergerakan mouse, serta memperbesar saat menggulir. Kami akan memilih browser untuk transformasi kami. Senjata, dalam hal ini, tidak harus memilih.

Mesin negara

Perilaku sistem seperti itu dengan mudah dijelaskan oleh transisi antara negara mereka, yaitu mesin negara $\ delta: S \ rightarrow S$ dimana $\ delta$ - fungsi transisi antar negara, menampilkan banyak negara dengan sendirinya.

Dalam kasus kami, diagram keadaan terlihat seperti ini:

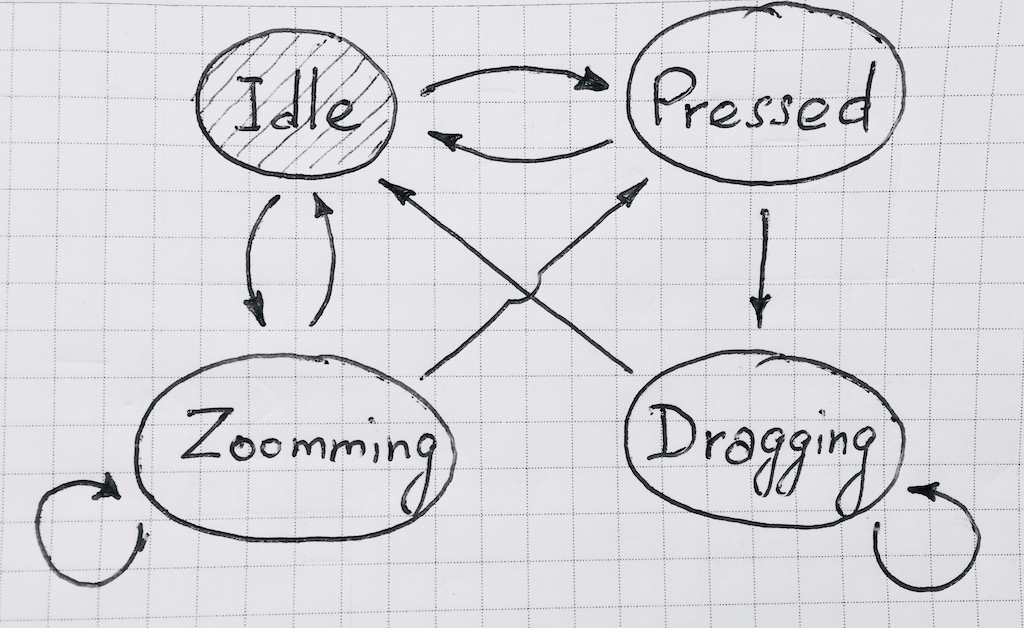
Saat mengimplementasikan fungsi transisi, akan lebih mudah untuk membuat event-dependent. Ini akan menjadi jelas di masa depan. Demikian pula, lebih mudah untuk berlangganan perubahan dalam kondisi mesin.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };

Kami akan menunda implementasi untuk sementara dan mengambil transformasi geometris yang mendasari tugas kami.

Geometri

Jika masalah dengan memindahkan kanvas begitu jelas sehingga kita tidak akan memikirkannya, maka peregangan harus dipertimbangkan secara lebih rinci. Pertama-tama, kita mengharuskan peregangan meninggalkan satu titik stasioner - kursor mouse. Kondisi reversibilitas juga harus dipenuhi, mis. urutan terbalik dari tindakan pengguna harus membawa kanvas ke posisi semula. Geometri apa yang cocok untuk ini? Kami akan mempertimbangkan beberapa kelompok transformasi titik pesawat menjadi dirinya sendiri $\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , yang umumnya diekspresikan oleh pengenalan variabel baru $x ', y'$ didefinisikan sebagai fungsi lama:

$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$

Sesuai dengan prinsip dualitas dalam matematika, transformasi seperti itu dapat diartikan sebagai perubahan dalam sistem koordinat, serta transformasi ruang itu sendiri dengan yang terakhir diperbaiki. Interpretasi kedua nyaman untuk tujuan kita.

Pemahaman modern tentang geometri berbeda dari pemahaman orang kuno. Menurut F. Klein , - studi geometri invarian sehubungan dengan kelompok transformasi tertentu. Jadi, dalam kelompok gerakan $D$ invarian adalah jarak antara dua titik $d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . Ini termasuk tanda hubung paralel $T _ {(x, y)}$ pada vektor $(x, y)$ rotasi $R _ {\ phi}$ relatif terhadap asal pada suatu sudut $\ phi$ dan refleksi $M_ {l}$ relatif terhadap beberapa baris $l$ . Gerakan seperti itu disebut elementer. Komposisi dari dua gerakan ini adalah milik kelompok kami dan terkadang turun ke tingkat dasar. Jadi, misalnya, dua pantulan cermin berurutan relatif terhadap garis lurus $l$ dan $n$ berikan rotasi di sekitar pusat tertentu pada sudut tertentu (periksa sendiri):

$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$

Tentunya Anda sudah menebak kelompok gerakan yang demikian $D$ membentuk geometri Euclidean. Namun, peregangan tidak menjaga jarak antara dua titik, tetapi hubungan mereka. Oleh karena itu, sekelompok gerakan, meskipun harus dimasukkan dalam skema kami, tetapi hanya sebagai subkelompok.

Geometri yang sesuai dengan kita didasarkan pada kelompok peregangan $P$ di mana, di samping gerakan-gerakan di atas, homothety ditambahkan $S_ {k}$ dengan koefisien $k$ .

Nah, yang terakhir. Elemen terbalik harus ada dalam grup. Dan karena itu ada yang netral $e$ (atau tunggal) yang tidak mengubah apa pun. Sebagai contoh

$S_ {k} \ circ S_ {k} ^ {- 1} = e$

berarti peregangan pertama

$k$ kali dan kemudian

$1 / k$ .

Sekarang kita dapat menggambarkan peregangan, membiarkan titik kursor mouse tetap, dalam bahasa teori-kelompok:

$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clientY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$

Catatan 1

Dalam kasus umum, pengaturan ulang tindakan tidak bersifat komutatif (Anda dapat melepas mantel Anda terlebih dahulu dan kemejanya, tetapi tidak sebaliknya).

$\ forall (x, y) \ in \ mathbb {R} ^ 2 \ neq 0 \ Rightarrow T _ {(- x, -y)} \ circ S_ {k} \ circ T _ {(x, y)}) \ neq S_ {k} \ circ T _ {(- x, -y)} \ circ T _ {(x, y)})$

Ekspresikan gerakannya $T _ {(x, y)}$ dan $S_ {k}$ dan komposisinya sebagai fungsi vektor dalam kode

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);

Nyeri 1

Sangat aneh bahwa dalam JavaScript tidak ada overloading operator. Tampaknya dengan penggunaan vektor dan grafik raster yang begitu luas, akan jauh lebih mudah untuk bekerja dengan vektor atau bilangan kompleks dalam bentuk "klasik". Konsep tindakan akan menggantikan operasi aritmatika. Jadi, misalnya, rotasi di sekitar beberapa vektor $a$ di sudut $\ phi$ akan diekspresikan dengan cara sepele:

$T _ {- a} \ circ R _ {\ phi} \ circ T_ {a} \ Leftrightarrow z \ rightarrow (z-a) e ^ {i \ phi} + a$

Sayangnya, JS tidak mengikuti perkembangan ide Pythagoras yang indah "Dunia adalah angka", tidak seperti, setidaknya, Python.

Perhatikan bahwa sejauh ini kami telah bekerja dengan sekelompok transformasi berkelanjutan. Namun, komputer tidak bekerja dengan kuantitas kontinu, oleh karena itu, mengikuti Poincare, kita akan memahami grup kontinu sebagai grup operasi diskrit tanpa batas. Sekarang kita telah menemukan geometri, kita harus beralih ke relativitas gerak.

Kosmologi kanvas. Grid modular

Selama seabad, sebagai manusia, perluasan alam semesta telah diketahui. Mengamati objek yang jauh, seperti galaksi dan quasar, kami mendaftarkan pergeseran spektrum elektromagnetik menuju gelombang yang lebih panjang, yang disebut pergeseran merah kosmologis. Setiap pengukuran menghubungkan pengamat, yang diamati dan sarana pengukuran dalam kaitannya dengan yang kita lakukan pengukuran kita. Tanpa alat ukur, tidak mungkin untuk membangun hubungan invarian di alam, yaitu untuk menentukan geometri alam semesta. Namun, geometri kehilangan maknanya tanpa dapat diamati. Jadi dalam tugas kita, senang memiliki landmark, seperti galaksi, sehubungan dengan cahaya yang kita dapat menentukan relativitas pergerakan kanvas kita. Struktur seperti itu bisa berupa kisi periodik, yang bercabang dua kali setiap kali ruang diperluas dua kali.

Karena kisi bersifat periodik, maka nyaman untuk mengadopsi aljabar modular. Dengan demikian, kami akan bertindak sebagai kelompok $P$ juga pada torus $T ^ 2 = S ^ 1 \ kali S ^ 1$ . Karena layar monitor bukan bidang yang kontinu, tetapi kisi integer $\ mathbb {Z} ^ 2$ (Kami mengabaikan sekarang bahwa itu terbatas), maka tindakan kelompok $P$ harus dipertimbangkan pada torus bilangan bulat $\ mathbb {Z} _ {p} ^ 2$ dimana $p$ - ukuran tepi kotak $p \ kali p$ :

Jadi, sekali dan untuk semua memperbaiki torus kami di dekat asal, kami akan melakukan semua perhitungan lebih lanjut di atasnya. Kemudian menyebarkannya menggunakan metode perpustakaan kanvas standar. Begini tampilan langkah satu piksel:

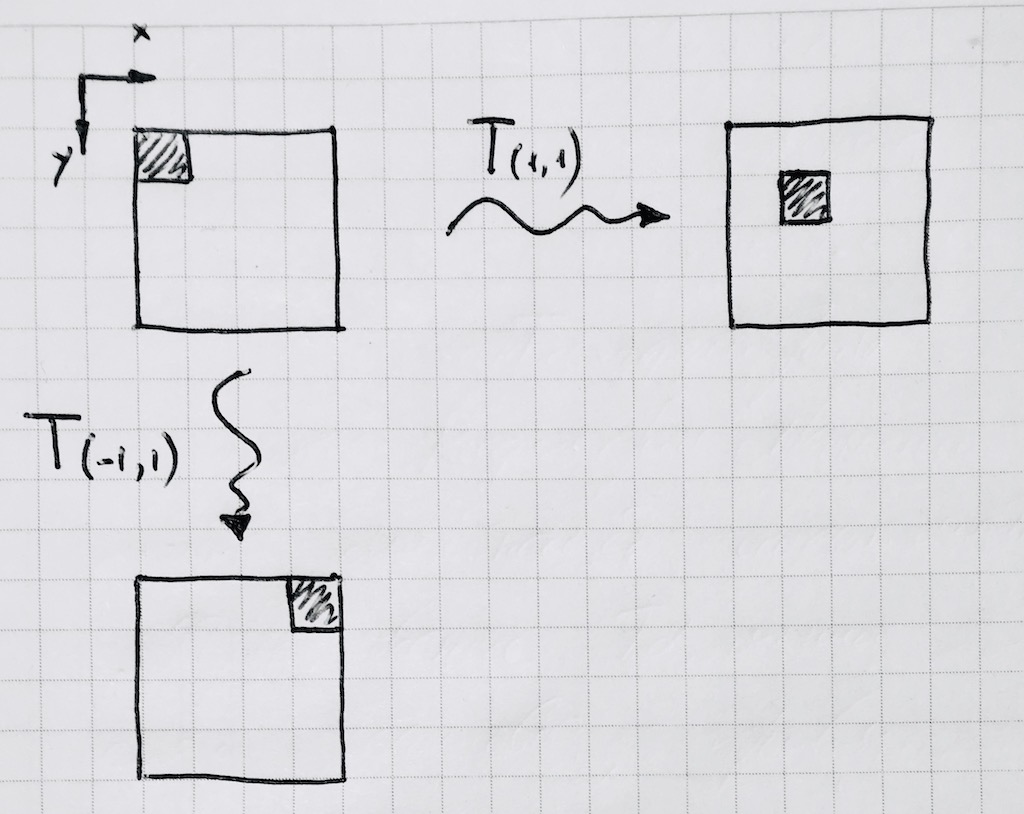
Jelas, operasi standar mengambil modul x% p tidak cocok untuk kita, karena menerjemahkan nilai-nilai negatif dari argumen menjadi yang negatif, tetapi pada torer bilangan bulat tidak ada. Tulis fungsi Anda $x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;

Sekarang kembali ke mesin keadaan akhir dan

mendefinisikannya

Kelas FSM dengan mudah diwarisi dari EventEmitter, yang akan memberi kita kemampuan untuk berlangganan.

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } }

Selanjutnya, tentukan skema transisi, buat kanvas dan

inisialisasi semuanya.

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm);

Maka Anda harus menentukan fungsi rendering, mengatur nilai awal yang diperlukan dan berlangganan perubahan status. Pertimbangkan bagian paling menarik dari kode:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });

Pertama, kita tidak memperluas dengan koefisien k, tetapi dengan beberapa rasio nk / k. Ini disebabkan oleh fakta bahwa m-step pemetaan kita pada titik yang tetap $(a, b)$ dinyatakan sebagai

$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$

atau, relatif terhadap nilai awal $x_ {1}, y_ {1}$

$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$

Jelas produknya $\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ ada fungsi nonlinier dari langkah iterasi dan sangat cepat menyatu dengan nol, atau melarikan diri hingga tak terbatas dengan penyimpangan awal yang kecil.

Kami memperkenalkan variabel g, yang merupakan ukuran menggandakan kanvas kami. Jelas, itu mengambil nilai konstan pada interval tertentu. Untuk mencapai linearitas $k_ {i} ^ *$ kami menggunakan subtitusi homogen

$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$

Maka semua anggota dalam pekerjaan, kecuali yang pertama dan terakhir, akan berkurang:

$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$

Lebih jauh, fase lompat g mengurangi laju ekspansi sedemikian rupa sehingga struktur fraktal yang terbentang di depan kita selalu bergerak secara linear. Dengan demikian, kita mendapatkan variasi perkiraan hukum kekuatan Hubble dari ekspansi Semesta.

Masih memahami batas-batas akurasi model kami.

Fluktuasi kuantum. Bidang angka 2-adic

Memahami proses pengukuran menyebabkan konsep bilangan real. Prinsip ketidakpastian Heisenberg menunjukkan batasnya. Komputer modern tidak bekerja dengan bilangan real, tetapi dengan kata-kata mesin, panjangnya ditentukan oleh kapasitas prosesor. Kata-kata mesin membentuk bidang angka 2-adic $\ mathbb {Q_ {2}}$ dan dilambangkan sebagai $\ mathbb {F_ {2} ^ {n}}$ dimana $n$ - panjang kata. Proses pengukuran dalam kasus ini digantikan oleh proses perhitungan dan dikaitkan dengan metrik non-Archimedean:

$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$

Dengan demikian, model kami memiliki batas perhitungan. Batasannya dijelaskan dalam standar IEEE_754 . Mulai pada titik tertentu, ukuran dasar kami akan melampaui batas akurasi dan operasi pengambilan modul akan mulai menghasilkan kesalahan yang menyerupai urutan pseudo-acak. Ini hanya diverifikasi dengan menghapus garis

 if (g < min || g > max) return;

Batas akhir dalam kasus kami dihitung dengan metode semi-empiris, karena kami bekerja dengan beberapa parameter.

Kesimpulan

Dengan demikian, nampaknya jauh pada pandangan pertama, teori terhubung pada kanvas di browser. Konsep tindakan, pengukuran, dan perhitungan terkait erat satu sama lain. Masalah menggabungkan mereka masih belum terselesaikan.