Diskusi mengenai pro dan kontra dari format floating-point Posit revolusioner baru sedang berlangsung. Argumen berikutnya dalam diskusi adalah
pernyataan bahwa sebenarnya tugas Posit adalah menyimpan data secara kompak dan tidak digunakan sama sekali dalam perhitungan; pada saat yang sama, perhitungan itu sendiri dilakukan dalam aritmatika Quire dengan akurasi yang lebih besar, yang juga termasuk dalam standar Posit.
Nah, simpan jadi toko. Apa artinya "menyimpan" angka setelah perhitungan dilakukan dengan akurasi yang lebih besar dari yang dimungkinkan oleh format penyimpanan? Itu berarti pembulatan, dan pembulatan berarti membuat kesalahan. Kesalahan dapat diperkirakan dengan berbagai cara - dan agar tidak terulang, hari ini kami menggunakan analisis spektral menggunakan transformasi Fourier.
Pengantar yang sangat singkat
Jika kita mengambil sinyal dalam bentuk sinusoid dan melakukan transformasi Fourier, maka dalam spektrum kita harus mendapatkan puncak tunggal; pada kenyataannya, spektrum dapat mengandung harmonisa dengan frekuensi yang merupakan kelipatan dari nada dasar yang diperoleh sebagai akibat dari distorsi nonlinear, dan rak kebisingan yang diperoleh sebagai hasil dari kebisingan, gangguan, dan digitalisasi. Di sini kita akan mengukur tingkat kebisingan ini.
Mulai
Untuk membuatnya lebih menarik, sebagai sinyal uji kami tidak hanya mengambil satu sinusoid, tetapi beberapa; perlu untuk memastikan bahwa periode sinusoid ini pas dengan periode transformasi Fourier diskrit. Di Wolfram Mathematica, ini bisa dilakukan, misalnya, seperti ini:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
Bilangan prima digunakan di sini untuk penipisan frekuensi yang tidak merata; dan j * j menggeser fase sinusoid tergantung pada frekuensi untuk menghindari lonjakan kuat dalam sinyal uji, memberikannya dengan amplitudo yang kurang lebih seragam. Sinyal yang diterima secara visual terlihat seperti ini:
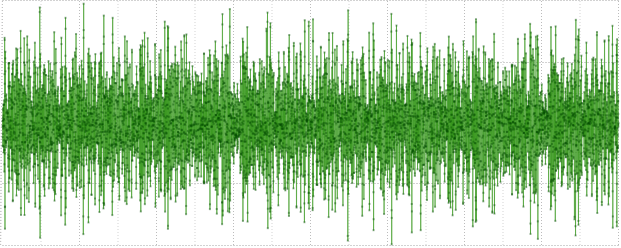
Selanjutnya, kita menormalkannya menjadi satu dengan nilai maksimum, lalu mengonversinya menjadi integer 32-bit Int, Float, Posit dan lagi menjadi Double. Jika klaim penulis benar, maka kesalahan yang diperkenalkan oleh Double → Posit → Transformasi ganda akan lebih dekat ke Doublé daripada ke Float.
Kami akan menganalisis tingkat kebisingan dalam unit standar untuk pemrosesan sinyal - desibel, yang memungkinkan kami membandingkan nilai pada skala logaritmik. Sebagai alat, saya menggunakan penganalisa spektrum saya sendiri, yang pernah ditulis untuk tujuan penelitian.
Jadi:
biru - mengapung
merah - Posit
ungu - Int32
biru - Ganda
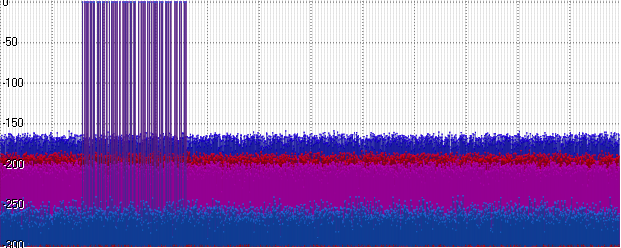
Posit, tentu saja, ternyata sedikit lebih baik daripada Float - tetapi dia masih jauh dari level Double. Dan pada saat yang sama - lebih buruk dari Int32! Masuk akal - karena sebagian bit membutuhkan urutan besarnya ... Mari gunakan urutan ini - tingkatkan amplitudo sinyal kami menjadi 1000:
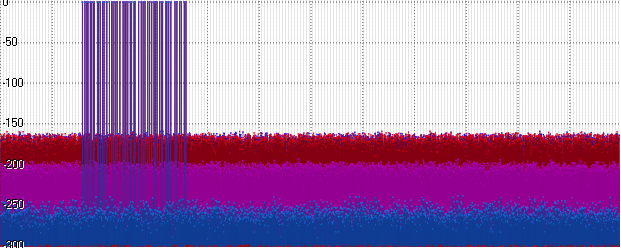
Tiba-tiba (dan sebenarnya cukup diharapkan), kebisingan di Float dan Posit menyusul. Teruskan - tingkatkan amplitudo menjadi satu miliar:
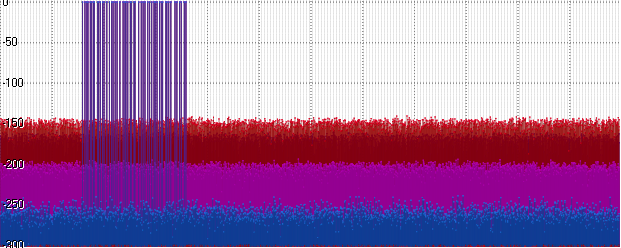
Float menunjukkan level yang sama, dan Posit mulai tertinggal. Peningkatan amplitudo lebih lanjut (di sini 10
15 ) mengarah ke peningkatan lebih lanjut di rak kebisingan:
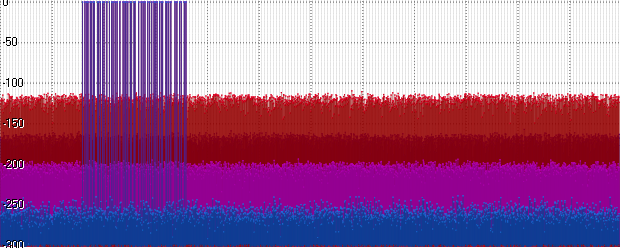
Kesimpulan
Keajaiban masih belum terjadi. Analisis spektral tidak mengkonfirmasi klaim penulis bahwa menggunakan format Posit sebagai penyimpanan dapat memberikan akurasi yang mendekati Double. Bahkan dalam kondisi terbaik, rak kebisingan di Posit hanya 20 desibel lebih rendah dari Float, tetapi pada saat yang sama lebih tinggi dari Int32 dengan 10 desibel, dan lebih tinggi dari Double dengan 60 desibel.
Tentu saja, Posit dapat dengan baik menemukan aplikasi yang berguna - sebagai perlindungan agar tidak melampaui batas yang diizinkan, ketika emisi secara signifikan melebihi nilai normal tidak akan mengarah pada kliping atau luapan. Tetapi bahkan dalam skenario ini, Posit bertindak lebih seperti kompromi antara Int dan Float, daripada format angka yang jelas lebih baik.