Hai
Dalam "artikel" ini, atau lebih tepatnya esai, saya akan menunjukkan cara yang sangat sederhana untuk bersenang-senang mengetahui dasar-dasar lateks dan python.
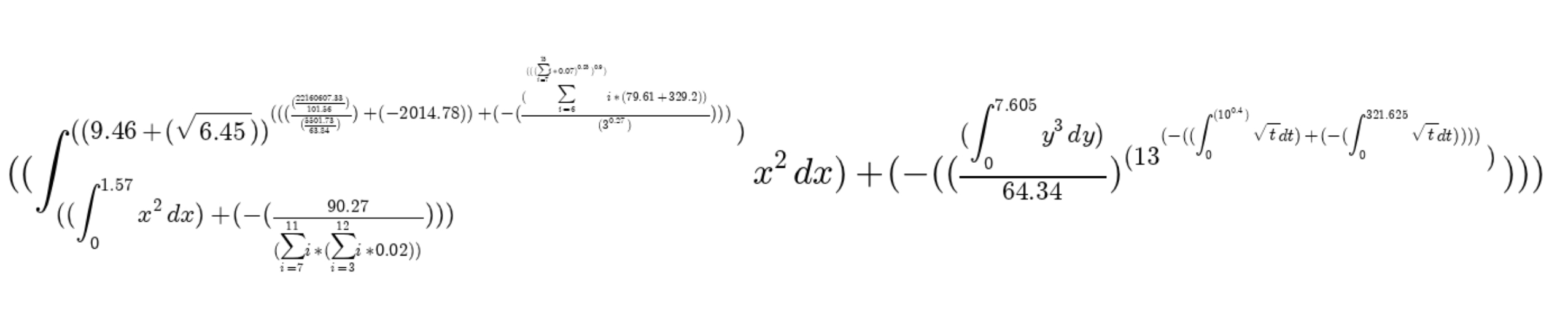
Mengapa
Nah, Anda dapat menghasilkan ekspresi sederhana untuk dihitung anak-anak. Atau seperti itu saja. Ya, setidaknya pasang di wallpaper, jika Anda fanatik seperti saya.
Bagaimana cara kerjanya?
Idenya benar-benar sangat sederhana, benar-benar siapa pun dapat menulis program seperti itu. Kami ingin menghasilkan ekspresi yang sama dengan beberapa angka n (yang dimasukkan pengguna). Angka apa pun dapat diganti dengan ekspresi aritmatika, misalnya, 3 = 1 + 2. Dan 2 adalah 4 / 2. Ini adalah bagaimana kami menghasilkan 3 = 1 + 4/2. Demikian pula, kami memperkenalkan beberapa operasi berbeda dan membungkusnya dalam LaTeX, bahasa formula.
Anda akan membutuhkan ...Pengalaman satu minggu di python dan matplotlib. Saya serius.
Mekanisme utama
Kita perlu mem-parsing ekspresi untuk mendapatkan angka dari sana. Mari kita sebut kelas kita sebagai penghasil masalah (kita semua sangat merindukannya!)
import random from math import log import math import sys sys.setrecursionlimit(1000)
Arti fungsi extract_nums adalah untuk mendapatkan n pasangan angka (a, b), di mana a adalah posisi karakter pertama, b adalah posisi + 1 terakhir.
Misalnya, jika kita menjalankan kode berikut:
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))
Kita akan melihat:
[(0, 2), (3, 6), (7, 10), (11, 13)]
Artinya, ini adalah array tuple. (0, 2) berarti ada angka antara 0 (inklusif) dan 2 (tidak inklusif).
Sekarang kami ingin membuat operator yang berbeda, mari kita mulai dengan perkalian dan penjumlahan. Nyatakan tiga fungsi
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + b
Esensi dari fungsi unmin tidak hanya mengubah semua argumen menjadi string, tetapi juga untuk mengurung salah satu operan jika kurang dari nol. Misalnya, kami mendapat angka a = 3, b = -4. Jika kita menulis
a = 3 b = -4 a, b = unmin(a, b)
Kemudian a = "3", b = "(- 4)"
Nah, fungsi lainnya jelas: __c_sum mengembalikan string dari bentuk "13 + 4", dan __c_mul "13 * 4".
Tetap menggabungkan dua bagian ini dan mengganti setiap angka dalam ekspresi dengan ekspresi.
Tambahkan kode berikut ke ProblemGenerator:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e
complexify mengambil beberapa angka, dan mengembalikan string - ekspresi yang rumit. Misalnya, jika kita menulis:
gen = ProblemGenerator() gen.add_expander(__c_sum) print(gen.complexify(13))
Kami mendapatkan:
31.2 + (-18.2)
Bagaimana cara kerja __rxp__? Kami secara acak memilih posisi angka dari ekspresi (misalnya, jika ada ekspresi "13 + 35/45", maka katakanlah kami memilih (3, 5)) dan mengganti angka ini dengan ekspresi yang sama dengan angka itu. Yaitu, saya ingin:
"13 + 35/45" - angka acak (3, 5)
"13+" + "(12 + 23)" + "/ 45"
"13+ (12 + 23) / 45"
Begitulah cara kerja __rxp__
Yah, randexpr bekerja cukup sederhana. Misalnya, jika kita memiliki empat langkah, maka ekspresi akan terbuka seperti ini:
13 (5.62 + 7.38) ((20.63 + (-15.01)) + 7.38) ((20.63 + (-(67.5 + (-52.49)))) + 7.38) ((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
Mari kita coba jalankan:
gen = ProblemGenerator() gen.add_expander(__c_sum) gen.add_expander(__c_mul) exp = gen.randexpr(1, 5) print(exp)
Hasil:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
LaTeX
Cukup aneh, sisa-sisa yang paling sederhana. Kami akan mengumumkan sejumlah operator LaTeX yang berbeda:
def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c
Tambahkan semua fungsi ke gen:
gen = ProblemGenerator() gen.add_expander(__l_sum)
Akhirnya, tambahkan output dari hasilnya:
import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
Itu saja.
Seluruh kode import random from math import log import math import sys sys.setrecursionlimit(1000) class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)] def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b, acc=5) return a + " * " + b def __c_sub(num): a = num + 100 ** (random.random() * 2) b = (a - num) a, b = unmin(a, b) return a + " - " + b def __c_log(num): fr = random.randint(300, 500) a = math.e ** (num / fr) a, fr = unmin(a, fr, acc=5) return "log(" + a + ") * " + fr def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c gen = ProblemGenerator() gen.add_expander(__l_sum) gen.add_expander(__l_div) gen.add_expander(__l_pow) gen.add_expander(__l_sqrt) gen.add_expander(__l_int) gen.add_expander(__l_sig) import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
Hasil (3 tangkapan layar)