Hipotesis "sensitivitas" membingungkan banyak ilmuwan komputer terkemuka, tetapi bukti barunya ternyata sangat sederhana sehingga satu peneliti dapat menguranginya menjadi tweet tunggal.
Karya yang diterbitkan musim panas ini mengakhiri hampir 30 tahun sejarah hipotesis mengenai struktur blok-blok pembangun dasar sirkuit komputer. Hipotesis "sensitivitas" ini telah membingungkan banyak ilmuwan komputer terkemuka selama bertahun-tahun, tetapi bukti barunya ternyata sangat sederhana sehingga seorang peneliti dapat menguranginya menjadi satu tweet.
"Hipotesis ini adalah salah satu tugas terbuka yang paling menjengkelkan dan memalukan di semua kombinatorik dan informatika teoretis,"
tulis Scott Aaronson dari University of Texas di Austin di blognya. "Daftar orang yang mencoba membuktikannya dan gagal melakukannya adalah daftar orang yang paling menonjol dalam matematika diskrit dan ilmu komputer teoretis," tambahnya dalam email.
Hipotesis ini dikaitkan dengan fungsi Boolean - aturan untuk mengubah string bit yang masuk (nol dan satu) menjadi bit tunggal. Satu aturan tersebut menghasilkan 1 ketika semua bit yang masuk adalah 1, dan 0 sebaliknya; aturan lain mengembalikan 0 jika baris berisi jumlah genap unit, dan 1 dalam kasus lain. Setiap sirkuit komputer adalah kombinasi dari fungsi Boolean, yang membuat mereka "bahan bangunan dari segala sesuatu yang dilakukan dalam ilmu komputer," kata
Rocco Cenedio dari Universitas Columbia.
Selama bertahun-tahun, banyak cara telah dikembangkan dalam ilmu komputer untuk mengukur kompleksitas fungsi Boolean yang diberikan. Setiap ukuran menggunakan aspeknya sendiri tentang bagaimana informasi jalur input menentukan bit output. Misalnya, "sensitivitas" fungsi Boolean, secara kasar, menunjukkan kemungkinan bahwa mengubah bit tunggal pada input akan mengubah bit pada output. Dan "kompleksitas permintaan" menghitung berapa banyak bit yang masuk harus diminta untuk mengetahui dengan pasti apa yang akan keluar.
Setiap ukuran memberikan sudut pandang uniknya sendiri pada struktur fungsi Boolean. Namun, para ilmuwan komputer menemukan bahwa hampir semua langkah-langkah ini cocok dengan platform universal, dan bahwa dengan nilai salah satu dari mereka kira-kira dapat menilai signifikansi yang lain. Dan hanya satu ukuran kompleksitas yang tidak cocok dengan skema ini: sensitivitas.
Pada tahun 1992, Noam Nisan dari Hebrew University of Jerusalem dan Mario Szeged, yang sekarang bekerja di Rutgers University, menyarankan bahwa sensitivitas masih cocok dengan platform ini. Tapi tidak ada yang bisa membuktikannya. "Pertanyaan ini, saya akan katakan, luar biasa di bidang mempelajari fungsi Boolean," kata Cenedio.
"Orang-orang menulis karya yang panjang dan rumit, berusaha membuat sedikit kemajuan," kata Ryan O'Donnell dari Carnegie Mellon University.
Dan sekarang,
Hao Huang , seorang ahli matematika dari Universitas Emory, telah membuktikan hipotesis sensitivitas dengan bantuan bukti dua halaman yang brilian namun elementer terkait dengan kombinatorik poin pada kubus. "Ini indah, seperti mutiara yang berharga," tulis Claire Matthew, dari Pusat Penelitian Ilmiah Negara Bagian Perancis dalam sebuah wawancara di Skype.
Aaronson dan O'Donnell menyebut karya Juan "buku" sebagai bukti hipotesis sensitivitas, merujuk pada konsep "buku surgawi" dari Pal Erdös, di mana Tuhan menuliskan bukti ideal setiap teorema. "Sulit bagi saya untuk membayangkan bahwa bahkan Tuhan tahu bukti sederhana dari teorema sensitivitas," tulis Aaronson.
Topik sensitif
Bayangkan, kata Matthew, bahwa Anda mengisi formulir dengan pertanyaan pada formulir aplikasi pinjaman bank, jawabannya bisa ya / tidak. Setelah selesai, bankir akan mengevaluasi hasilnya dan memberi tahu Anda apakah Anda layak untuk mendapat pinjaman. Proses ini adalah fungsi Boolean: jawaban Anda adalah bit masuk, dan keputusan bankir keluar.
Jika aplikasi Anda ditolak, Anda dapat memikirkan apakah Anda dapat mengubah hasilnya dengan berbohong dalam satu pertanyaan - mungkin dengan menyatakan bahwa Anda berpenghasilan lebih dari $ 50.000 setahun, meskipun tidak demikian. Jika kebohongan ini mengubah hasil pertimbangan, ilmuwan komputer akan menyebut fungsi Boolean sedemikian "sensitif" terhadap nilai bit tertentu. Jika, misalnya, Anda dapat berbaring di salah satu dari tujuh tempat, dan setiap kali mengubah hasilnya, maka sensitivitas fungsi Boolean dalam mengevaluasi aplikasi pinjaman Anda adalah tujuh.
Ilmuwan komputer mendefinisikan sensitivitas keseluruhan fungsi Boolean sebagai nilai sensitivitas tertinggi untuk semua opsi yang mungkin untuk mengisi aplikasi. Dalam arti tertentu, ukuran ini menghitung berapa banyak masalah yang akan sangat penting dalam kebanyakan kasus batas - dalam aplikasi, yang hasilnya paling mudah diubah jika aplikasi itu sendiri sedikit dimodifikasi.
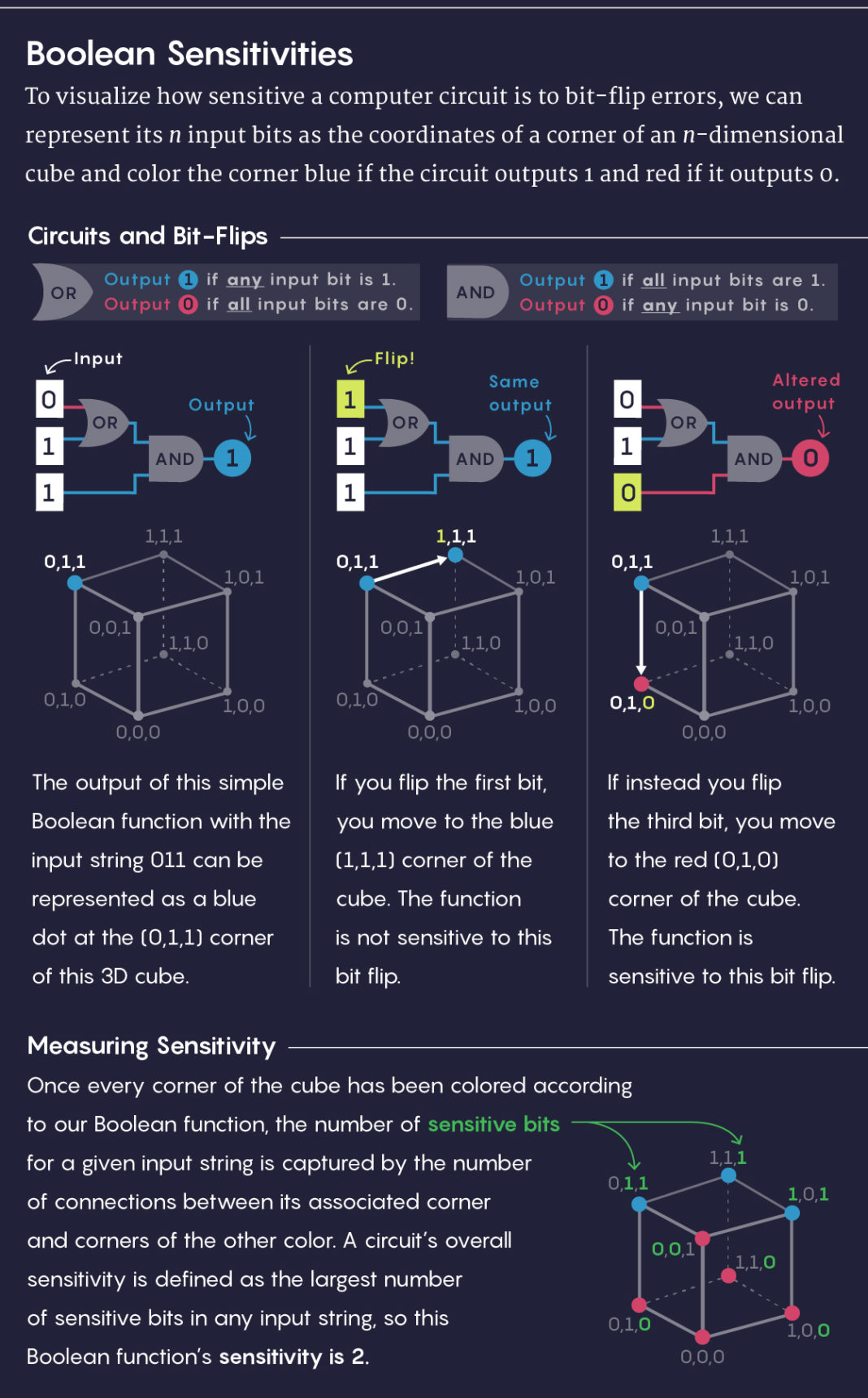Untuk memvisualisasikan sensitivitas rangkaian terhadap kesalahan dengan pembalikan bit, n bit yang masuk dapat direpresentasikan sebagai koordinat dari simpul kubus n-dimensi. Kami akan mewarnai titik biru jika jalur menghasilkan 1, dan merah jika 0.
Di kiri tengah: output dari fungsi Boolean sederhana dengan input 011 dapat diwakili oleh titik biru di bagian atas kubus (0,1,1).
Tengah: Memutar bit pertama, kita akan pergi ke bagian atas kubus biru (1,1,1). Fungsi tidak peka terhadap inversi bit ini.
Di kanan tengah: Putar bit ketiga, kita akan pergi ke puncak merah kubus (0,1,0). Fungsi ini peka terhadap pembalikan bit ini.
Setelah mewarnai semua simpul dari kubus, kita mendapatkan jumlah bit sensitif untuk garis masuk yang diberikan sama dengan jumlah koneksi antara simpul yang sesuai dan simpul dari warna yang berbeda. Sensitivitas loop didefinisikan sebagai jumlah bit sensitif terbesar dalam setiap jalur input, sehingga fungsi ini memiliki sensitivitas 2.Sensitivitas biasanya merupakan salah satu ukuran termudah untuk menghitung kompleksitas, tetapi sama sekali bukan ukuran penjelasan yang sederhana. Misalnya, bankir kami, alih-alih memberi Anda formulir untuk diisi, bisa mulai dengan satu pertanyaan, dan kemudian menggunakan jawaban Anda untuk menentukan pertanyaan mana yang akan ditanyakan selanjutnya. Jumlah pertanyaan terbesar yang harus ditanyakan seorang bankir sebelum mencapai suatu keputusan adalah kerumitan meminta fungsi Boolean.
Ukuran seperti itu muncul dalam berbagai situasi - misalnya, dokter mungkin ingin mengirim pasien untuk mengumpulkan tes sesedikit mungkin untuk membuat diagnosis, atau ahli pembelajaran mesin mungkin ingin membuat algoritma yang mempelajari beberapa properti dari objek mungkin sebelum dia akan dapat mengklasifikasikannya dengan benar. "Dalam banyak situasi - diagnostik atau pelatihan - Anda menyukai aturan dasar untuk memiliki kompleksitas kueri yang rendah," kata O'Donnell.
Di antara langkah-langkah lainnya adalah pencarian cara paling sederhana untuk menulis fungsi Boolean dalam bentuk ekspresi matematika, atau untuk menghitung berapa banyak jawaban yang harus ditunjukkan bankir kepada bos untuk membuktikan bahwa aplikasi telah diproses dengan benar. Bahkan ada varian kompleksitas kueri dari fisika kuantum, ketika bankir menanyakan "superposisi" beberapa pertanyaan pada saat bersamaan. Memahami bagaimana ukuran ini terkait dengan ukuran kompleksitas lainnya, para peneliti lebih memahami keterbatasan algoritma kuantum.
Ilmuwan komputer telah membuktikan bahwa ada hubungan yang erat antara semua tindakan ini, dengan pengecualian sensitivitas. Lebih khusus, mereka menemukan bahwa mereka terkait satu sama lain oleh ketergantungan polinomial - misalnya, satu ukuran dapat dinyatakan sebagai kuadrat atau kubus yang lain. Dan hanya sensitivitas yang dengan keras kepala menentang, tidak ingin berintegrasi ke dalam skema klasifikasi yang nyaman ini. Banyak peneliti menduga bahwa itu harus sesuai untuk itu, tetapi tidak dapat membuktikan bahwa tidak ada fungsi Boolean aneh yang sensitivitasnya terhubung dengan ukuran lain bukan oleh polinomial tetapi oleh ketergantungan eksponensial, yang dalam hal ini berarti bahwa ukuran sensitivitas secara fundamental. lebih kecil dari yang lain.
"Pertanyaan ini membuat orang tetap terjaga selama 30 tahun," kata Aaronson.
Pojok solusinya
Juan mengetahui tentang hipotesis ini pada akhir 2012, saat makan malam dengan ahli matematika
Michael Sachs dari Institute for Advanced Studies, di mana Juan adalah seorang postdoc. Dia langsung terpesona oleh kesederhanaan dan keanggunan hipotesis. "Dan sejak saat itu aku menjadi terobsesi dengan pemikiran tentangnya," katanya.
Juan menambahkan hipotesis sensitivitas ke "daftar rahasia" masalah yang dia minati, dan ketika dia mengetahui tentang beberapa alat matematika baru, dia bertanya-tanya apakah dia bisa membantunya. "Setiap kali setelah publikasi karya lain, saya kembali ke tugas ini," katanya. "Tentu saja, saya mengalokasikan waktu dan energi untuk mengerjakan tugas yang lebih realistis."
Hao Huang pada liburan baru-baru ini di LisbonJuan, seperti banyak orang dalam komunitas penelitian, tahu bahwa hipotesis sensitivitas dapat dibuktikan jika matematikawan dapat membuktikan hipotesis lain dengan kondisi yang lebih sederhana mengenai sekumpulan titik pada kubus dimensi yang berbeda. Ada cara alami untuk beralih dari string nol dan yang ke titik pada kubus n-dimensi: cukup gunakan n bit sebagai koordinat titik itu.
Misalnya, empat garis dua bit - 00, 01, 10 dan 11 - sesuai dengan empat sudut kotak pada bidang dua dimensi: (0,0), (0,1), (1,0) dan (1,1). Demikian pula, delapan string tiga bit berhubungan dengan delapan sudut kubus tiga dimensi, dan seterusnya, untuk dimensi yang lebih tinggi. Fungsi Boolean dapat dianggap aturan mewarnai sudut kubus ini dengan dua warna berbeda (misalnya, merah untuk 0 dan biru untuk 1).
Pada tahun 1992,
Craig Gotsman , yang sekarang bekerja di Institut Teknologi New Jersey dan Nati Lignal dari Hebrew University, menyadari bahwa bukti hipotesis sensitivitas dapat direduksi menjadi jawaban atas pertanyaan sederhana tentang kubus dengan dimensi berbeda: jika Anda mengambil set yang terdiri lebih dari setengah simpul kubus , dan warna mereka merah, apakah ada titik merah yang terhubung ke banyak titik merah lainnya (dengan titik "terhubung" berarti dua simpul dihubungkan oleh tepi yang sama, dan tidak terletak secara diagonal).
Jika subset kami mengandung tepat setengah dari simpul kubus, mereka mungkin tidak terhubung satu sama lain. Misalnya, di antara delapan sudut kubus tiga dimensi ada empat poin,
(0,0,0), (1,1,0), (1,0,1) dan (0,1,1) terletak secara diagonal satu sama lain. Tetapi segera setelah lebih dari setengah dari simpul kubus dari dimensi apa saja menjadi merah, di antara mereka titik merah harus terhubung di antara mereka sendiri. Pertanyaannya adalah bagaimana koneksi ini didistribusikan? Apakah akan ada setidaknya satu dari puncak ini dengan lebih banyak koneksi?
Pada tahun 2013, Juan mulai berpikir bahwa cara terbaik untuk memahami masalah ini mungkin akan menggunakan metode standar untuk mewakili jaringan menggunakan matriks yang melacak titik mana yang terhubung, dan kemudian mempelajari banyak angka yang disebut nilai eigen dari matriks. Selama lima tahun dia secara berkala kembali ke ide ini, tetapi tidak berhasil. “Setidaknya karena apa yang saya pikirkan tentangnya sebelum tidur, lebih mudah bagi saya untuk tidur selama beberapa malam,” dia berkomentar di posting blog Aaronson.
Kemudian pada tahun 2018, Juan berpikir tentang menggunakan teorema pergantian Cauchy, sebuah pernyataan matematika 200 tahun yang lalu, yang menghubungkan nilai-nilai eigen dari sebuah matriks dengan submatrix, yang mungkin membuatnya menjadi alat yang ideal untuk mempelajari hubungan antara kubus dan subset dari simpulnya. Juan memutuskan untuk meminta hibah dari State Science Foundation untuk mengeksplorasi ide ini lebih lanjut.
Kemudian, bulan lalu, duduk di sebuah hotel di Madrid dan mengisi aplikasi hibah, dia tiba-tiba menyadari bahwa dia dapat memperpanjang penggunaan pendekatan ini sampai akhir, hanya mengubah tanda-tanda beberapa angka dari matriks. Dengan cara ini, ia dapat membuktikan bahwa dalam setiap set lebih dari setengah simpul dari kubus n-dimensi akan ada titik yang terkait dengan setidaknya di titik-titik lain - dan hipotesis sensitivitas segera mengikuti dari hasil ini.
Ketika Matthew menerima pekerjaan Juan melalui pos, reaksi pertamanya adalah "oops," katanya. "Ketika sebuah tugas telah ada selama 30 tahun dan semua orang mengetahuinya, maka buktinya harus sangat panjang dan kompleks, atau sangat dalam." Dia membuka file dengan pekerjaan itu, berharap bahwa dia tidak akan mengerti apa pun.
Namun, buktinya cukup sederhana sehingga Matthew dan peneliti lain dapat mencernanya dalam satu duduk. "Saya pikir pada musim gugur ini, para siswa akan memberitahunya sebagai bagian dari satu kuliah di setiap kursus master dalam kombinatorik," tulisnya di Skype.
Hasil Juan ternyata bahkan lebih kuat dari yang diperlukan untuk membuktikan hipotesis ini, dan kekuatan ini harus memberi kita ide-ide baru tentang ukuran kompleksitas. "Itu telah ditambahkan ke toolkit kami dan dapat membantu menjawab pertanyaan lain terkait fungsi Boolean," kata Cenedio.
Tetapi yang paling penting, hasil Juan memungkinkan kita untuk menghentikan semua kekhawatiran tentang apakah sensitivitas adalah alien yang aneh di dunia ukuran kompleksitas, kata Cenedio. "Saya pikir di malam hari, mengetahui hasil ini, sangat banyak yang bisa tidur nyenyak."