Bermain dengan bilangan kompleks

Hai

Esai lain. Kali ini mari kita bermain dengan bilangan kompleks, dengan rumus dan visualisasi mereka.

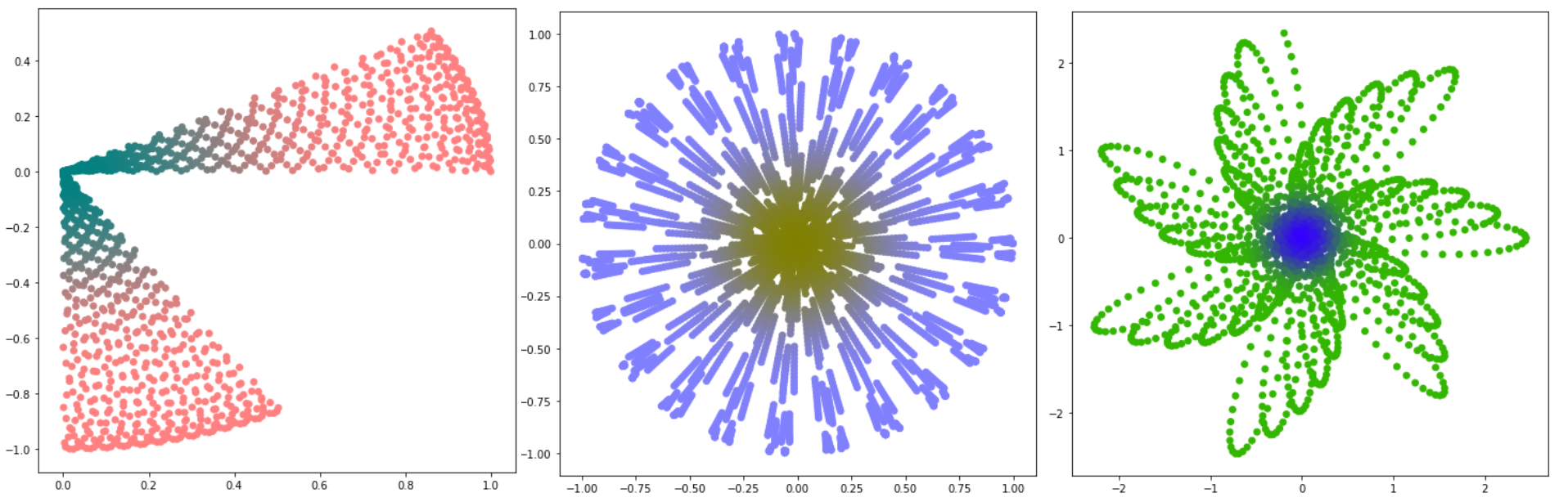
Ide

Bilangan kompleks adalah ekstensi tertentu dari bilangan real, pada kenyataannya suatu vektor yang mendefinisikan seluruh rangkaian aksioma. Setiap bilangan kompleks (dan karenanya nyata) dapat ditulis sebagai $$$z = a + bi$di mana a adalah bagian nyata, b adalah bagian imajiner, i adalah akar dari persamaan $$$x ^ {2} = - 1$. Banyak operasi didefinisikan untuk itu, yang didefinisikan untuk bilangan real, misalnya, $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$. Menariknya, jika Anda melakukan berbagai operasi dengan mereka, naikkan ke daya, berkembang biak, dll., Lalu ambil $$$Re (z)$(bagian nyata) untuk sumbu Ox, dan $$$Im (z)$(bagian imajiner) untuk poros Oy, Anda bisa mendapatkan gambar lucu.

Ngomong-ngomong, saya sendiri datang dengan semua formula berikut.

Fungsi visualisasi

Rutin. Fungsi, yang menurut fungsi berulang ini menarik semua yang ada di lapangan:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

Semua fungsi kita bergantung pada dua parameter A dan B. Selain itu, kita beralih ke B di dalam vis (), dan A adalah parameter global dari fungsi.

Fungsi Keriting

$$

$$f (A, B) = Bsin (B) * e ^ {iBcos (A)}$$

Pernyataannya dalam python:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Dan lari

 A = 121.5 vis(A, func_1, step=0.1) 

Dan hasil untuk A = 121.5:



Dan untuk A = 221.5:



Perhatikan bahwa angka-angka ini tidak mengikuti dari perhitungan integral yang pasti pada manifold halus dan kata-kata pintar lainnya yang tidak berarti dalam konteks ini. Ini adalah angka yang benar-benar acak, dan masih ada ketidak terhinggaan dari A yang berbeda, sebagai hasil dari keindahan yang diperoleh.

Perlu melukis

Kami mendeklarasikan fungsi warna (fungsi yang mengembalikan tupel tiga angka dalam koordinat):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

Pilih parameter A acak, biarlah 149:

 vis(149, func_1, step=0.1, c=color_1) 

Fungsi Angsa

Angsa diuraikan sebagai berikut:

$$

$$f (A, B) = cos (B) sin (B) * B * e ^ {iBcos (A)}$$

Deklarasi Python:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Hasilnya untuk A = 106:

Fungsi focaccia

$$

$$f (A, B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

Fungsi Tanpa Judul

$$

$$f (A, B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

Formula kecantikan

$$

$$f (A, B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

Itu saja untuk saat ini.