"Teknologi" untuk mendapatkan persamaan dinamika TAU. Dan mengapa Sistem Identifikasi menyebalkan, dan "fisika jujur" berkuasa

Ketika membahas artikel sebelumnya tentang desain berorientasi model, muncul pertanyaan yang masuk akal: jika kita menggunakan data percobaan, tetapi apakah mungkin untuk melakukan lebih mudah, memasukkan data dalam Identifikasi Sistem dan mendapatkan model objek tanpa repot dengan fisika sama sekali? Tanpa mempelajari segala macam rumus bertingkat Navier-Stokes, Bernoulli dan kompas caliper lainnya dengan Rabinovichi? Kami menguji objek - mendapat hasilnya.



Kami mempresentasikan model rudal FAU2 sebagai fungsi transfer tunggal, Anda dapat melihatnya di sini ... Dan, sepertinya, semuanya bekerja. Mengapa kita perlu mempelajari analisis matematika dan kalkulus diferensial terlebih dahulu ketika ada tombol ajaib yang mendapatkan model dari tes?

Memang, pendekatan ini dapat diterapkan, tetapi ini membutuhkan dua kondisi:

• Objek seharusnya sudah (tidak cocok untuk objek yang dirancang).
• Data pengukuran harus lengkap dan dapat diandalkan.

Dalam kasus lain - “mereka menginginkan yang terbaik, ternyata seperti biasa” (c).
Misalnya, dalam artikel ini tentang simulasi drive listrik, ditunjukkan bahwa "dengan nilai ambang batas tertentu dari keakuratan alat ukur, model drive menjadi tidak dapat diidentifikasi, yang mengarah pada hilangnya kemampuan kontrol dan ketidakmampuan untuk mendiagnosis"
Dalam artikel yang sama, kami akan menganalisis keajaiban dan keajaiban membuat model dalam bentuk fungsi transfer dari TAU, dan kemudian kami akan melakukan sesi mengekspos sihir ini.

Jadi sulap dulu

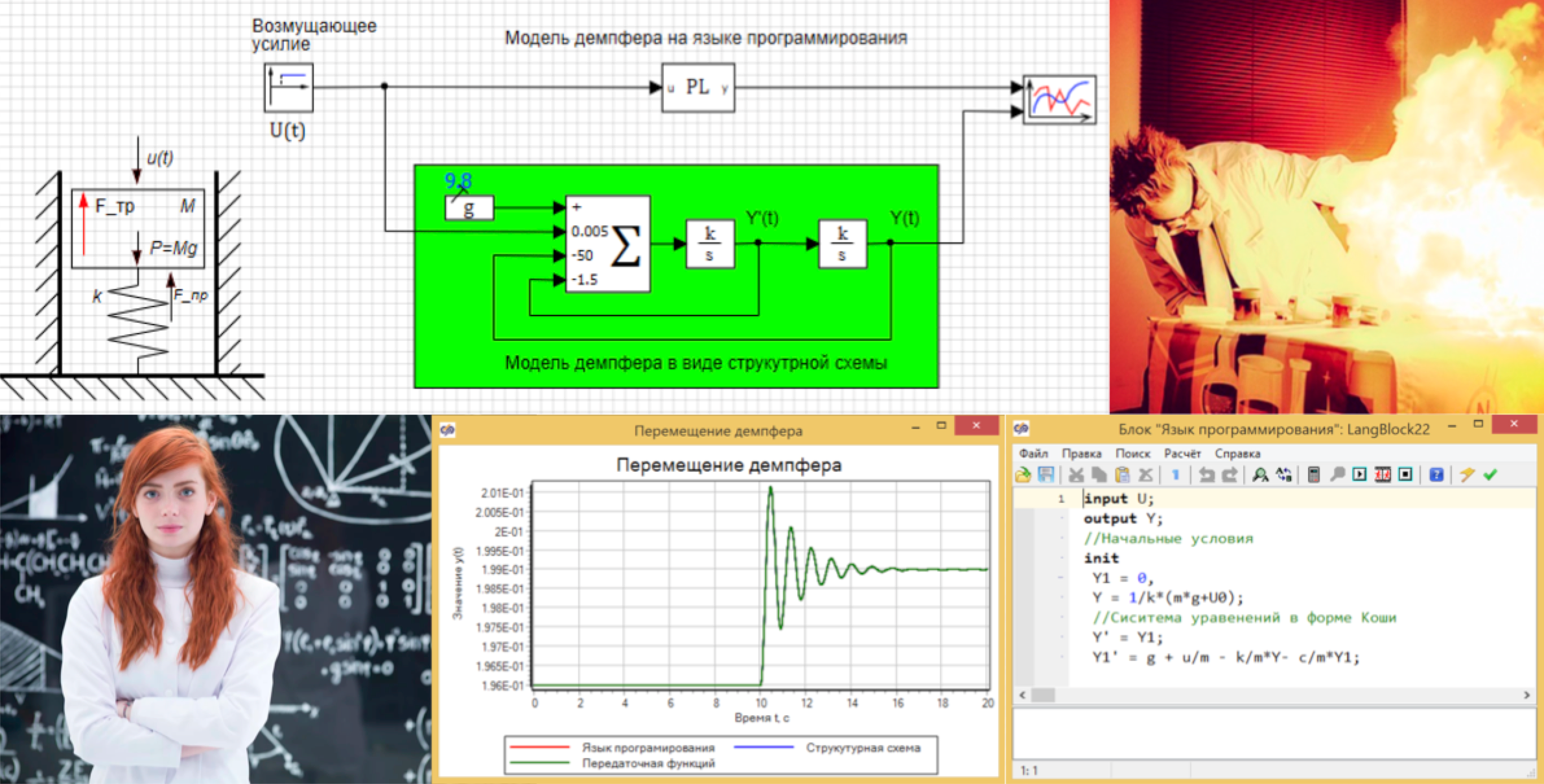
Mari kita lihat contoh sederhana ini. Kami memiliki model peredam mekanis. Ini adalah piston pada pegas, bergerak di dalam silinder, dapat bergerak ke atas dan ke bawah. Posisinya adalah fungsi Y (t) yang menarik bagi kami, gaya pengganggu (U (t)) bekerja di atasnya dari atas, dan gaya gesekan kental bekerja pada dinding piston. (Lihat Gambar 1)


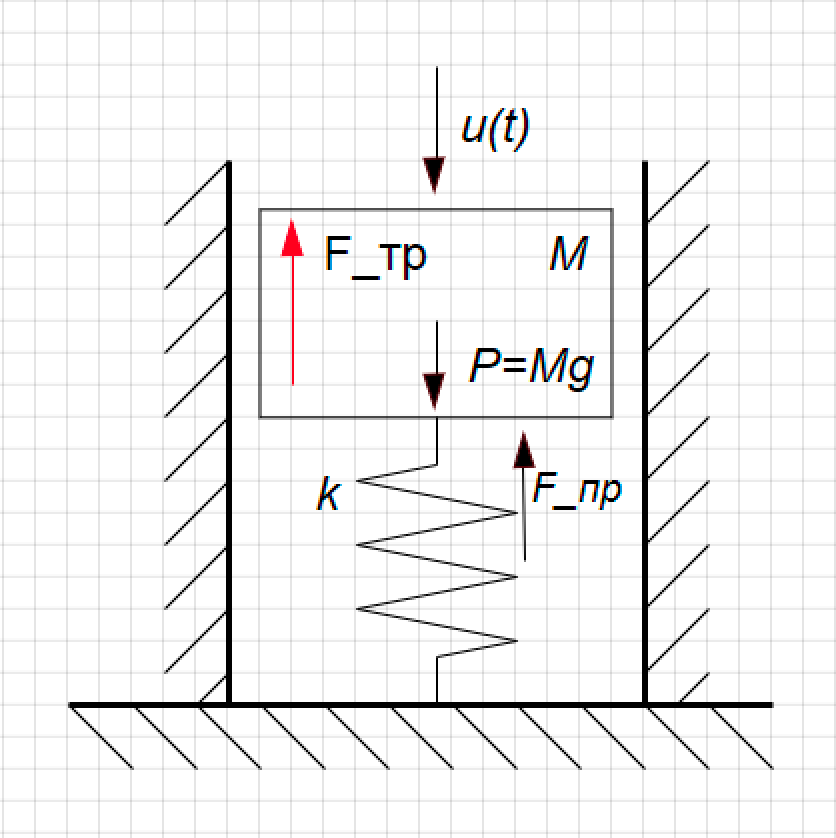Gambar 1. Desain shock absorber.

Kami memperoleh fungsi transfer untuk tautan ini.

Orang-orang Jedi yang sudah terbiasa dengan keajaiban fungsi transfer dapat melewati bagian ini dan langsung mengekspos keajaiban, dan untuk Padawan muda kami akan mengungkapkan seluruh teknologi untuk mendapatkan persamaan dinamis.

Menurut hukum ke-2 Newton, percepatan tubuh sebanding dengan jumlah gaya yang bekerja pada tubuh:

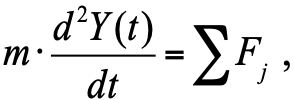
, (1)
di mana m adalah berat badan; F _j - gaya yang bekerja pada tubuh (piston peredam).
Mengganti dalam persamaan (1) semua gaya sesuai dengan Gambar. 1, kami memiliki:

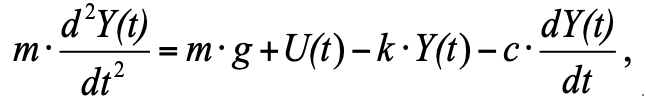
(2)
dimana:
Y (t) adalah posisi piston;
P = m ∙g - gravitasi;
F_pr = k ∙ Y (t) - kekuatan tahan pegas;
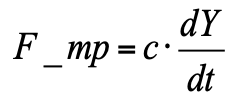
- gaya gesek kental (sebanding dengan kecepatan piston).
Dimensi gaya dan koefisien termasuk dalam persamaan (2):


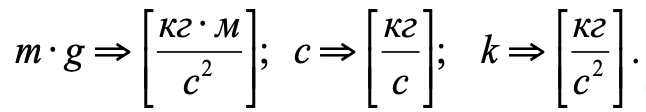
Kami percaya bahwa pada saat nol piston berada dalam kesetimbangan. Maka posisi awal piston adalah y ₀ dalam kesetimbangan, di mana kecepatan dan akselerasi adalah 0, dapat dihitung dari persamaan 2.



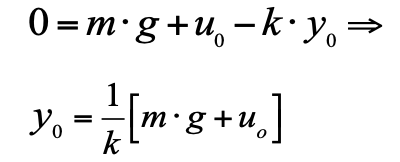
Persamaan ini memungkinkan Anda untuk menghitung pada posisi apa piston akan berada pada beban yang berbeda. Karakteristik statis ini: gaya yang diterapkan - perpindahan yang diterima. Tampilannya untuk sistem kami sangat sederhana (lihat Gambar 2):


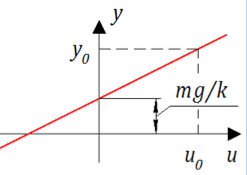Gambar 2. Karakteristik statis damper.

Tampaknya di sini kebahagiaan - garis sederhana, ketika diterapkan kekuatan, ia menerima perpindahan. Tapi itu dia! Kami tidak tertarik pada posisi akhir piston, tetapi pada proses transisi dari satu kondisi ke kondisi lainnya.

Untuk menganalisis proses sementara, teori pengendalian otomatis TAU dibuat. Menurut "teknologi untuk membuat model" yang khas menurut teori ini, diusulkan untuk mempertimbangkan sistem tidak dalam nilai absolut, tetapi dalam penyimpangan dari keadaan kesetimbangan. Pernyataan seperti itu menyederhanakan solusi dan konstruksi. Dan pada kenyataannya, jika kita mengganti nilai absolut dengan penyimpangan, kita mendapatkan:


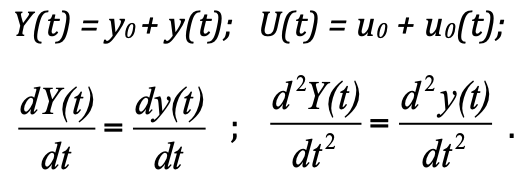F_pr = k ∙ (y ₀ + y (t)) = k ∙ y ₀ + k ∙ y (t) adalah kekuatan resistansi pegas;
- gaya gesekan.
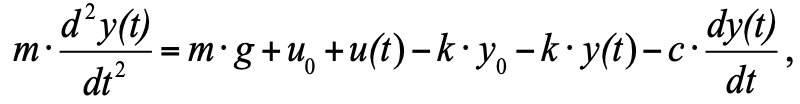
tetapi karena kita menerima bahwa pada saat awal kita memiliki keadaan keseimbangan, dan jumlah ketiga gaya dalam keadaan keseimbangan adalah nol, kita dapat menghilangkannya dari persamaan, dan sebagai hasilnya kita mendapatkan:

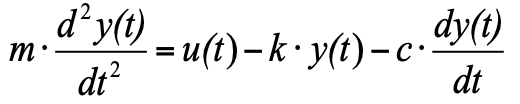
(4)
Untuk menerjemahkan persamaan ke bentuk sesuai dengan kanon TAU, Anda perlu membagi seluruh persamaan dengan k sehingga koefisien y, nilai variabel output sama dengan 1, dan mentransfer faktor dengan nilai output y (t) ke sisi kanan dan nilai input ke sisi kiri pengaruh u (t) :

(5)
Persamaan ini sudah dapat ditulis dalam bentuk operator:

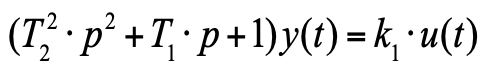
(6)
dimana:


p = d / dt adalah operator diferensiasi. Perhatikan bahwa dimensi koefisien memiliki dimensi dan makna konstanta waktu:



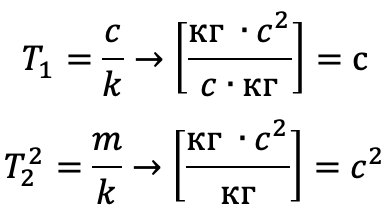
Fungsi transfer untuk persamaan seperti itu [6] memiliki bentuk:


Sekarang, di depan mata Anda, kami mendapatkan fungsi transfer dalam bentuk blok dari persamaan fisika, dan, lebih lanjut, blok yang dihasilkan adalah tautan osilasi standar dari TAU.

Bagi saya pribadi, keajaiban di sini adalah penampilan magis dari karakteristik statis, bagian-bagian dari sistem, massa piston, elastisitas pegas, gesekan pada dinding) dari objek secara ajaib muncul karakteristik sementara transien dalam sistem

Periksa formula dengan model

Seperti yang diajarkan Maxim Andreev kepada saya, ketika menciptakan model dinamis, "Akhir adalah kepala segalanya!" ( lihat di sini prinsip pemodelan kedua - "mulai dari akhir" ):

Dan pada akhir fungsinya, kita memiliki pergerakan.

Karena itu, Bayangkan Persamaan 2 dalam bentuk Cauchy, untuk bergerak.

Bentuk Cauchy adalah ketika di sebelah kiri adalah turunan dari fungsi yang menarik bagi kami, di sebelah kanan adalah ekspresi untuk perhitungan mereka. Karena turunan dalam persamaan adalah derajat kedua, memperkenalkan variabel baru Y1 - laju perubahan posisi (kecepatan perpindahan), kami memperoleh sistem dua persamaan dalam bentuk Cauchy:



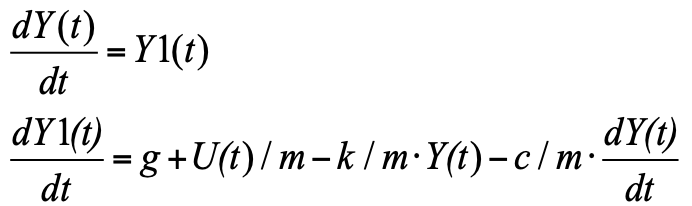
Persamaan ini dapat ditulis dalam blok "Bahasa pemrograman" dan mendapatkan modelnya (lihat Gambar 3):


Gambar 3. Model damper dalam bahasa pemrograman.

Sebagai input, kami menggunakan nilai gaya U, output dari blok adalah perpindahan Y, posisi awal diberikan oleh rumus 3. Semua variabel ditetapkan sebagai sinyal global untuk proyek:


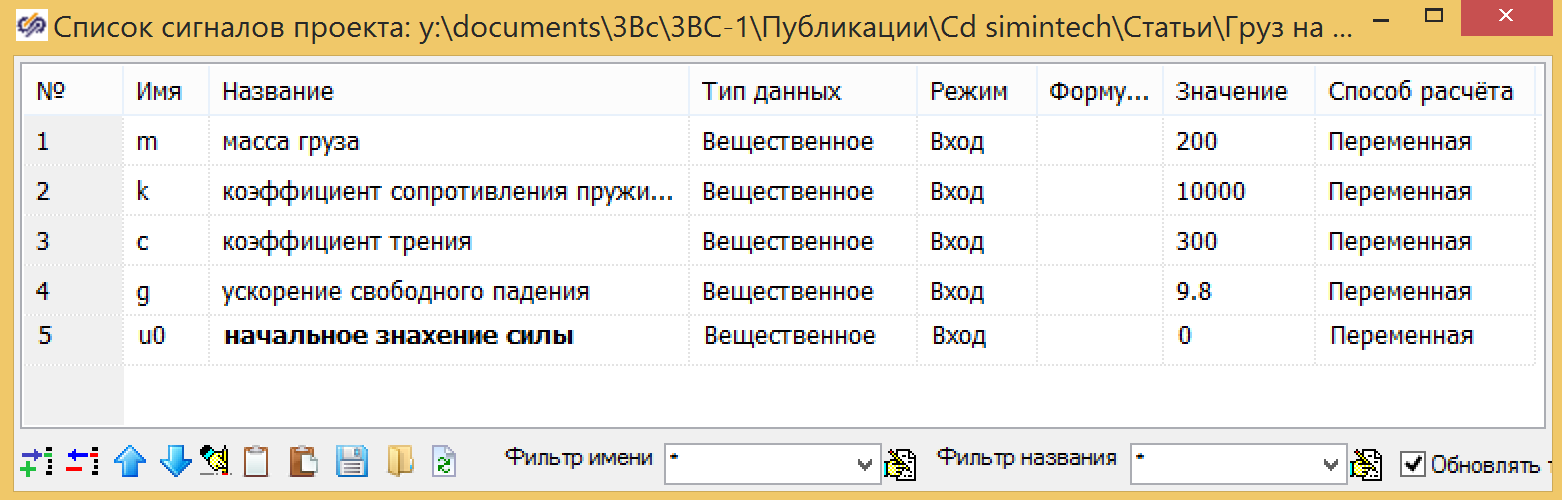Gambar 4. Variabel proyek global.

Model damper juga dapat dibuat dalam bentuk struktur, pada Gambar 5, yang menunjukkan model damper paralel yang dibuat dari blok standar, di mana kondisi awal berada di integrator pada output (lihat Gambar 6), dan koefisien dimasukkan dalam penambah (lihat Gambar. 7)


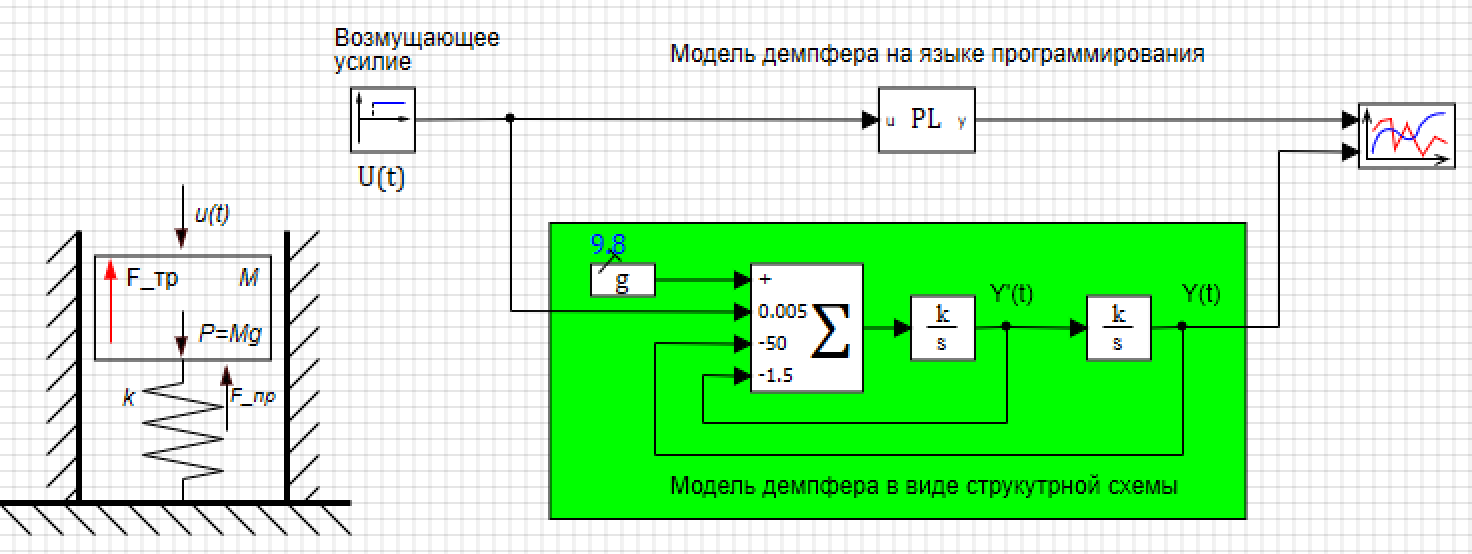Gambar 5. Peredam dalam bahasa pemrograman dan dalam bentuk diagram struktural.


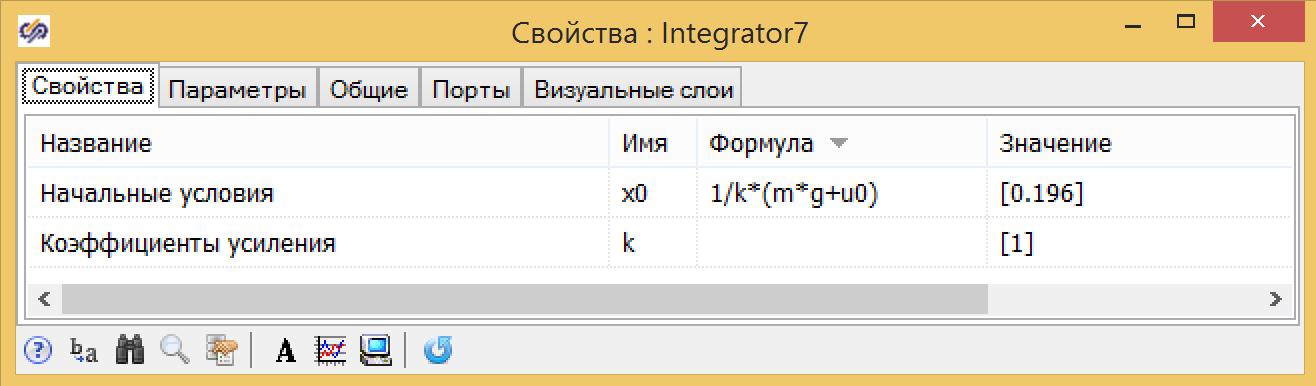Gambar 6. Properti integrator dengan kondisi awal.


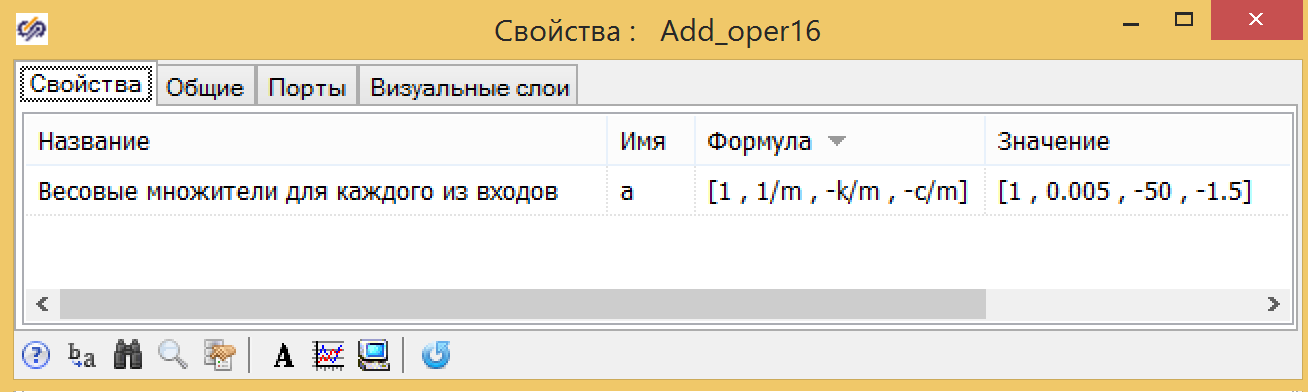Gambar 7. Properti dari penambah dengan koefisien.

Kami mengatur efek perturbing selama 10 detik, mengubah gaya akting dari 0 menjadi 30, dalam lompatan, dan memastikan bahwa kedua model menunjukkan hasil yang sama (lihat Gambar 8).


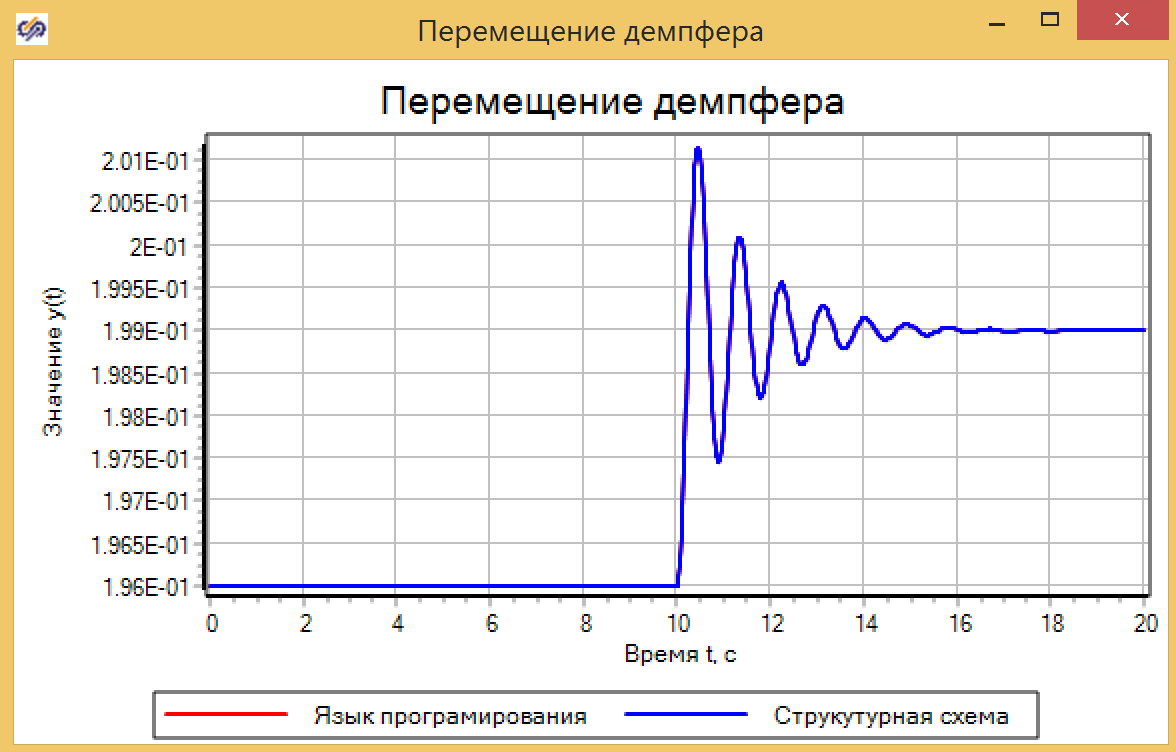Gambar 8. Memindahkan damper.

Mari kita periksa model dalam bentuk fungsi transfer dalam bentuk umum dan dalam bentuk tautan berosilasi, yang merupakan sistem ini. Untuk melakukan ini, kami merakit sirkuit, seperti yang ditunjukkan pada Gambar 9.


Gambar 9. Dua model damper dalam bentuk fungsi transfer.

Harus dipertimbangkan bahwa kita menyusun diagram dalam penyimpangan, oleh karena itu, untuk mendapatkan nilai absolut, perlu menambahkan konstanta - posisi awal piston.

Untuk fungsi transfer (rumus 7) kami menggunakan konstanta global yang sama dan ekspresi yang diperoleh sebelumnya untuk k1, T1, T2 (lihat Gambar 10).


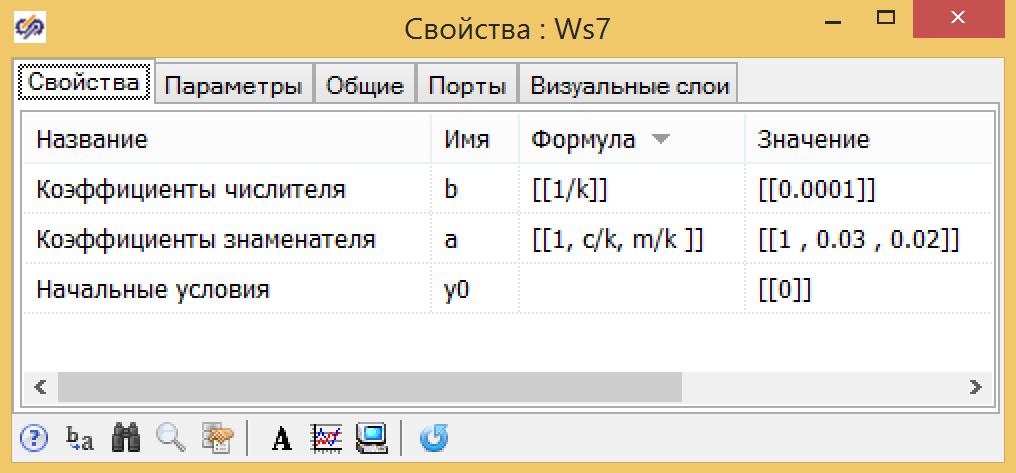Gambar 10. Parameter fungsi transfer dari bentuk umum.

Untuk parameter dari tautan getaran, rumusnya sedikit lebih rumit, tetapi mereka juga dapat dinyatakan dalam parameter global: massa piston m, koefisien hambatan pegas k, koefisien gesekan s (lihat Gambar 11).


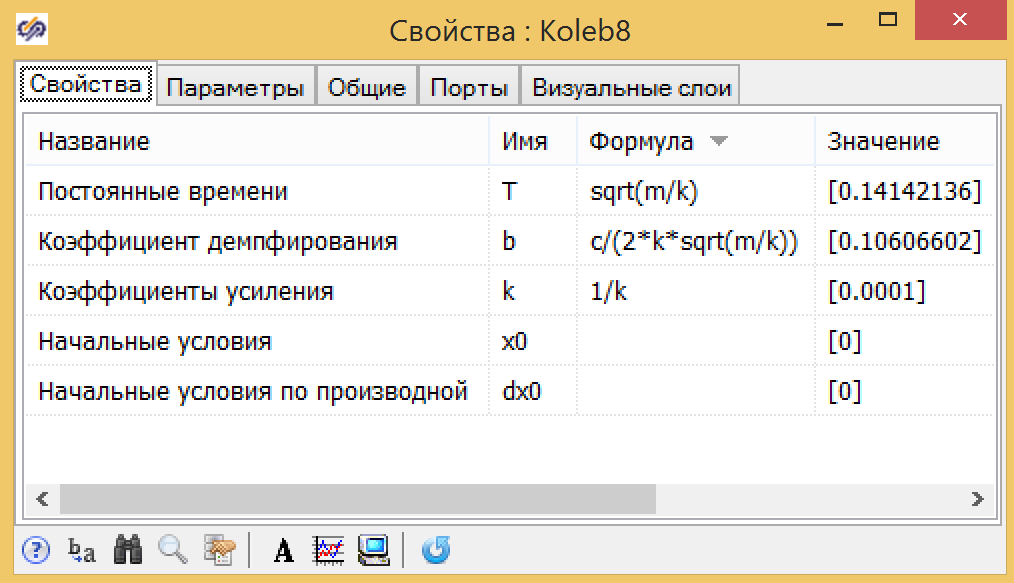Gambar 11. Parameter dari tautan getaran.

Grafik transisi menunjukkan (lihat Gambar 12) bahwa sihir TAU benar-benar berfungsi. Fungsi transfer memberikan hasil yang sama persis dengan model yang didasarkan pada persamaan fisika.


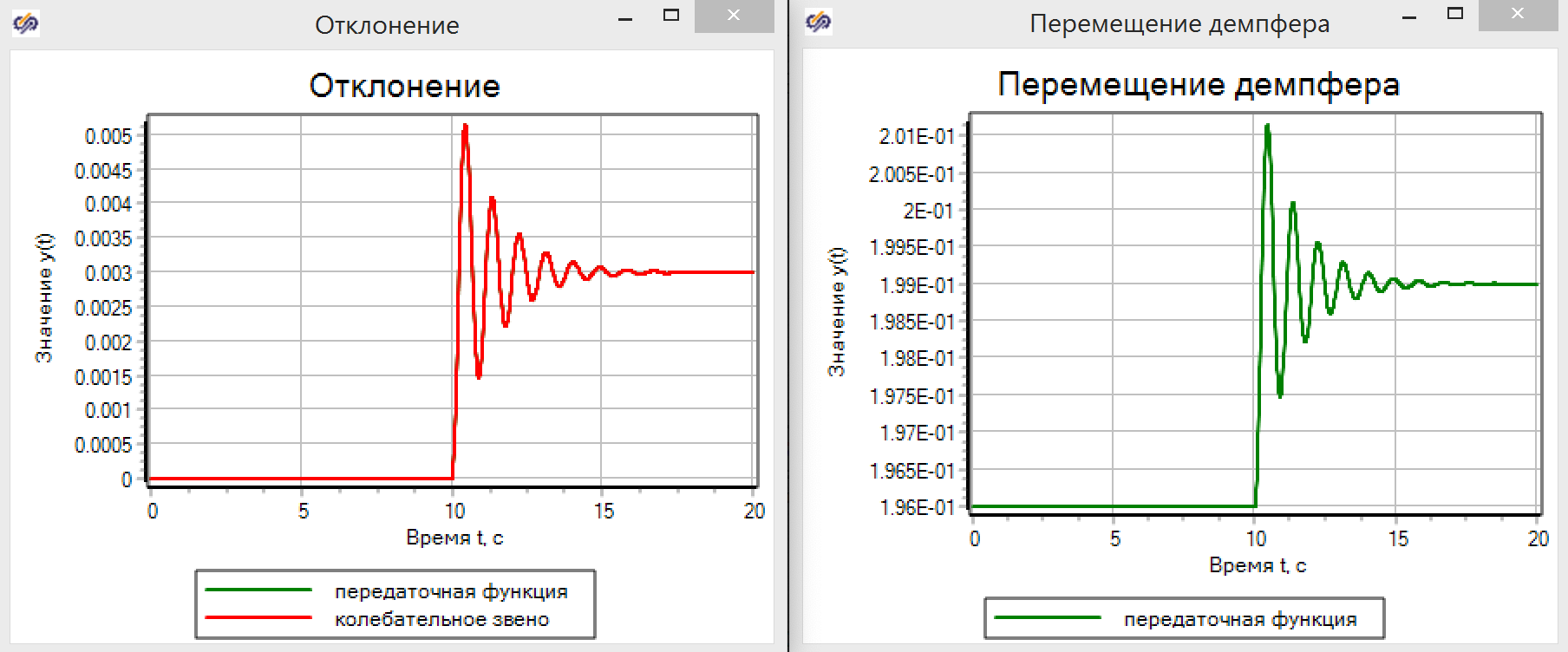Gambar 12. Memindahkan damper pada model TAU.

Bayangkan kita tidak memiliki model, dan kita menggunakan unit identifikasi sesuai dengan data yang diperoleh dari percobaan. Ada seluruh teknologi analisis data dan fungsi transfer, tetapi sebagai bagian dari artikel dan sebagai contoh, kami akan menghubungkan blok bangunan fungsi transfer ke model dalam bentuk bahasa pemrograman, seperti yang ditunjukkan pada Gambar 13. Kami percaya bahwa kami memiliki model "kotak hitam", dan kami tidak tahu apa yang ada di dalamnya.


Gambar 13. Skema koneksi pseudo-identifier.

Sebagai hasil dari analisis blok kami dalam bahasa pemrograman, kami memperoleh fungsi transfer, yang secara praktis tidak berbeda dari yang awal, berasal dari persamaan (lihat Gambar 14.). Bandingkan dengan gambar 10. Ini dia tombol ajaib!


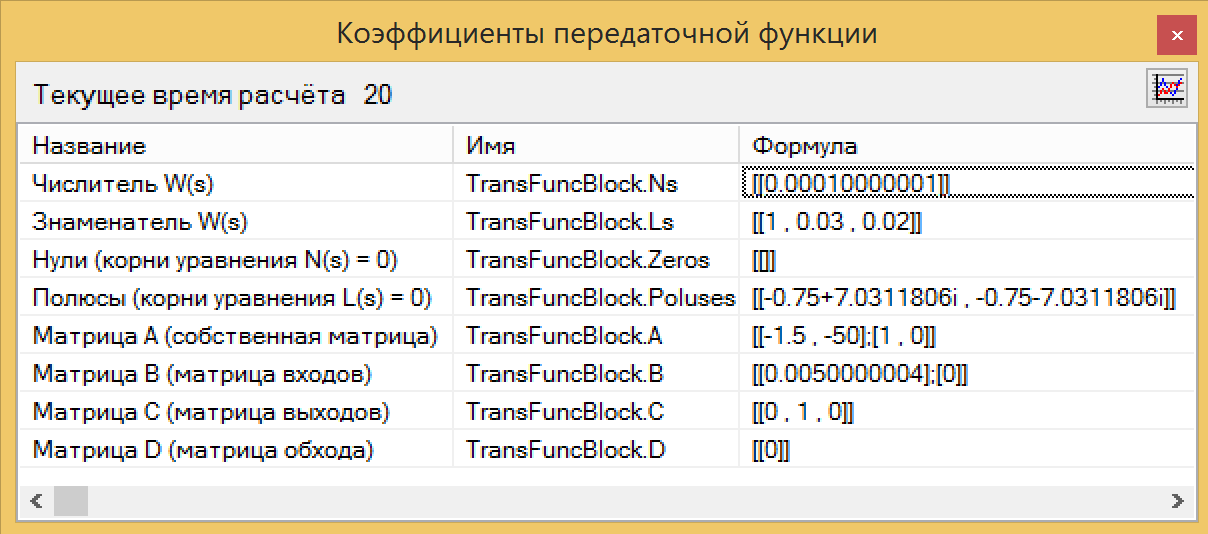Gambar 14. Identifikasi fungsi transfer.

Nilai pembilang dan penyebut dapat langsung disalin dari blok identifikasi, disisipkan ke dalam blok fungsi transfer dan pastikan grafiknya cocok. Sihir TAU bekerja.

Sesi mengekspos sihir

Jadi mengapa Anda tidak dapat selalu menggunakan Identifikasi Sistem untuk proses desain berorientasi model ketika semuanya begitu ajaib?

Untuk memahami kelemahan dari model yang diperoleh dengan mengidentifikasi kotak hitam Identifikasi Sistem, cobalah untuk menjawab pertanyaan sederhana: apa yang akan menjadi penyimpangan peredam ketika massa piston meningkat sebesar 30%?

Dan kemudian ternyata tidak semua yogurt sama bermanfaatnya.

Jika Anda memiliki persamaan jujur, Anda cukup mengubah massa beban dalam variabel global proyek dan mendapatkan proses transisi baru, dan fungsi transfer baru.



Dalam kasus ketika, alih-alih persamaan fisika yang jujur, Anda memiliki fungsi transfer siap pakai yang dibangun dari hasil percobaan, Anda perlu menjalankan lagi dan melakukan percobaan untuk memahami bagaimana perubahan massa akan mempengaruhi perilaku model. Seperti yang mereka katakan, kepala yang buruk tidak memberi istirahat pada kaki.

Kesimpulan:

1. Duduk dan berpikir tentang persamaan fisika selalu lebih bermanfaat dan lebih murah daripada bereksperimen.
2. Model yang berasal dari persamaan fisik proses jauh lebih enak dan lebih berguna daripada fungsi transfer.
3. Percobaan harus mengklarifikasi koefisien yang tidak diketahui atau sulit untuk mengukur parameter.
4. Belajar fisika dan Anda akan senang!

File dengan model damper untuk percobaan dapat diambil di sini ...