Nama saya Vyacheslav, saya seorang ahli matematika kronis dan selama beberapa tahun saya belum menggunakan siklus ketika bekerja dengan array ...
Tepat sejak saya menemukan operasi vektor di NumPy. Saya ingin memperkenalkan Anda dengan fungsi NumPy yang paling sering saya gunakan untuk memproses array data dan gambar. Di akhir artikel saya akan menunjukkan bagaimana Anda dapat menggunakan toolkit NumPy untuk menggabungkan gambar tanpa iterasi (= sangat cepat).
Jangan lupakan
import numpy as np
dan ayo pergi!
Isi
Apa itu numpy?Array penciptaanAkses ke elemen, irisanBentuk array dan perubahannyaPenataan ulang dan transposisi sumbuArray bergabungKloning dataOperasi matematika pada elemen arrayPerkalian matriksAgregatorAlih-alih sebuah kesimpulan - sebuah contohApa itu numpy?
Ini adalah pustaka sumber terbuka yang pernah dipisahkan dari proyek SciPy. NumPy adalah keturunan Numeric dan NumArray. NumPy didasarkan pada perpustakaan LAPAC, yang ditulis dalam Fortran. Alternatif non-python untuk NumPy adalah Matlab.
Karena NumPy didasarkan pada Fortran, itu adalah perpustakaan cepat. Dan karena mendukung operasi vektor dengan array multidimensi, sangat nyaman.
Selain versi dasar (array multidimensi dalam versi dasar), NumPy mencakup serangkaian paket untuk menyelesaikan tugas-tugas khusus, misalnya:
- numpy.linalg - mengimplementasikan operasi aljabar linier (perkalian vektor dan matriks dalam versi dasar);
- numpy.random - mengimplementasikan fungsi untuk bekerja dengan variabel acak;
- numpy.fft - mengimplementasikan transformasi Fourier langsung dan terbalik.
Jadi, saya mengusulkan untuk mempertimbangkan secara rinci hanya beberapa fitur NumPy dan contoh penggunaannya, yang akan cukup bagi Anda untuk memahami seberapa kuat alat ini!
<up>Array penciptaan
Ada beberapa cara untuk membuat array:
- convert list to array:
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- salin array (salin dan salin dalam wajib !!!):
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- buat nol atau satu array ukuran tertentu:
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
Atau ambil dimensi dari array yang ada:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- saat membuat array persegi dua dimensi, Anda bisa menjadikannya unit diagonal matrix:
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- membangun array angka dari Dari (termasuk) ke Ke (tidak termasuk) dengan langkah Langkah:
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
Secara default, dari = 0, langkah = 1, sehingga varian dengan satu parameter ditafsirkan sebagai Ke:
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
Atau dengan dua - seperti Dari dan Ke:
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
Perhatikan bahwa dalam metode No. 3, dimensi array dilewatkan sebagai
satu parameter (tupel ukuran). Parameter kedua dalam metode No. 3 dan No. 4, Anda dapat menentukan jenis elemen array yang diinginkan:
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
Menggunakan metode astype, Anda bisa melemparkan array ke tipe yang berbeda. Jenis yang diinginkan ditunjukkan sebagai parameter:
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
Semua tipe yang tersedia dapat ditemukan di kamus sctypes:
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<up>Akses ke elemen, irisan
Akses ke elemen array dilakukan oleh indeks integer, hitungan mundur dimulai dari 0:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
Jika Anda membayangkan array multidimensi sebagai sistem array satu dimensi bersarang (array linier, elemen yang dapat berupa array linear), menjadi jelas bahwa Anda dapat mengakses subarrays menggunakan kumpulan indeks yang tidak lengkap:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
Dengan paradigma ini, kita dapat menulis ulang contoh akses ke satu elemen:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
Ketika menggunakan kumpulan indeks yang tidak lengkap, indeks yang hilang secara implisit diganti oleh daftar semua indeks yang mungkin ada di sepanjang sumbu yang sesuai. Anda dapat melakukan ini secara eksplisit dengan mengatur ":". Contoh sebelumnya dengan satu indeks dapat ditulis ulang sebagai berikut:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
Anda dapat melewati indeks sepanjang sumbu atau sumbu apa pun; jika sumbu diikuti oleh sumbu dengan indeksasi, maka ":" harus:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
Indeks dapat mengambil nilai integer negatif. Dalam hal ini, hitungannya adalah dari akhir array:
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
Anda dapat menggunakan bukan indeks tunggal, tetapi daftar indeks di sepanjang setiap sumbu:
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
Atau rentang indeks dalam bentuk "Dari: Ke: Langkah". Desain ini disebut slice. Semua elemen dipilih sesuai dengan daftar indeks mulai dari indeks Dari secara inklusif, hingga indeks Ke yang tidak
termasuk dengan langkah Langkah:
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
Langkah indeks memiliki nilai default 1 dan dapat dilewati:
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
Nilai Dari dan Ke juga memiliki nilai default: 0 dan ukuran array di sepanjang sumbu indeks, masing-masing:
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
Jika Anda ingin menggunakan Dari dan Ke secara default (semua indeks pada sumbu ini) dan langkahnya berbeda dari 1, maka Anda perlu menggunakan dua pasang titik dua agar interpreter dapat mengidentifikasi parameter tunggal sebagai Langkah. Kode berikut "memperluas" array di sepanjang sumbu kedua, tetapi tidak berubah di sepanjang yang pertama:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
Sekarang mari kita lakukan
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
Seperti yang Anda lihat, melalui B kami mengubah data dalam A. Itulah mengapa penting untuk menggunakan salinan dalam tugas nyata. Contoh di atas akan terlihat seperti ini:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
NumPy juga menyediakan kemampuan untuk mengakses berbagai elemen array melalui array indeks boolean. Array indeks harus cocok dengan bentuk yang diindeks.
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
Seperti yang Anda lihat, konstruksi seperti itu mengembalikan array datar yang terdiri dari elemen-elemen dari array yang diindeks yang sesuai dengan indeks yang sebenarnya. Namun, jika kita menggunakan akses seperti itu ke elemen-elemen array untuk mengubah nilainya, maka bentuk array akan dipertahankan:
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Operasi logis logical_and, logical_or, dan logical_not didefinisikan di atas indexing array Boolean dan melakukan operasi logis AND, OR, dan NOT elementwise:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
logical_and dan logical_atau ambil 2 operan, logical_not ambil satu. Anda dapat menggunakan operator &, | dan ~ untuk menjalankan AND, OR, dan NOT, masing-masing, dengan sejumlah operan:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Yang setara dengan hanya menggunakan I1.
Dimungkinkan untuk mendapatkan array logis pengindeksan yang sesuai dalam bentuk array nilai dengan menulis kondisi logis dengan nama array sebagai operan. Nilai boolean indeks akan dihitung sebagai kebenaran ekspresi untuk elemen array yang sesuai.
Temukan array pengindeksan elemen I yang lebih besar dari 3, dan elemen dengan nilai kurang dari 2 dan lebih dari 4 - akan diatur ulang ke nol:
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<up>Bentuk array dan perubahannya
Array multidimensi dapat direpresentasikan sebagai array satu dimensi dengan panjang maksimum, dipotong menjadi beberapa bagian di sepanjang sumbu terakhir dan diletakkan di lapisan di sepanjang sumbu, dimulai dengan yang terakhir.
Untuk kejelasan, pertimbangkan sebuah contoh:
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
Dalam contoh ini, kami membentuk 2 array baru dari array satu dimensi dengan panjang 24 elemen. Array B, ukuran 4 oleh 6. Jika Anda melihat urutan nilai, Anda dapat melihat bahwa di sepanjang dimensi kedua ada rantai nilai yang berurutan.
Dalam array C, 4 oleh 3 oleh 2, nilai kontinu berjalan di sepanjang sumbu terakhir. Sepanjang sumbu kedua adalah blok secara seri, kombinasi yang akan menghasilkan baris sepanjang sumbu kedua array B.
Dan mengingat bahwa kami tidak membuat salinan, menjadi jelas bahwa ini adalah berbagai bentuk representasi dari array data yang sama. Oleh karena itu, Anda dapat dengan mudah dan cepat mengubah bentuk array tanpa mengubah data itu sendiri.
Untuk mengetahui dimensi array (jumlah sumbu), Anda dapat menggunakan bidang ndim (angka), dan untuk mengetahui ukuran sepanjang setiap bentuk sumbu (tuple). Dimensi juga bisa dikenali dari panjang bentuk. Untuk mengetahui jumlah total elemen dalam array, Anda bisa menggunakan nilai ukuran:
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
Perhatikan bahwa ndim dan bentuk adalah atribut, bukan metode!
Untuk melihat array satu dimensi, Anda dapat menggunakan fungsi ravel:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
Untuk mengubah ukuran sepanjang sumbu atau dimensi, gunakan metode membentuk kembali:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
Penting agar jumlah elemen dipertahankan. Kalau tidak, akan terjadi kesalahan:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
Mengingat bahwa jumlah elemen adalah konstan, ukuran sepanjang sumbu satu ketika membentuk kembali dapat dihitung dari nilai panjang sepanjang sumbu lainnya. Ukuran sepanjang satu sumbu dapat ditunjuk -1 dan kemudian akan dihitung secara otomatis:
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
Anda dapat menggunakan bentuk ulang alih-alih berlepasan:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
Pertimbangkan aplikasi praktis dari beberapa fitur untuk pemrosesan gambar. Sebagai objek penelitian, kami akan menggunakan foto:
Mari kita coba unduh dan visualisasikan menggunakan Python. Untuk ini kita perlu OpenCV dan Matplotlib:
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
Hasilnya akan seperti ini:
Perhatikan bilah unduhan:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
OpenCV bekerja dengan gambar dalam format BGR, dan kami terbiasa dengan RGB. Kami mengubah urutan byte sepanjang sumbu warna tanpa mengakses fungsi OpenCV menggunakan konstruk
"[:,:, :: :: 1]".
Kurangi gambar sebanyak 2 kali pada setiap sumbu. Gambar kami memiliki dimensi genap di sepanjang sumbu, masing-masing, dapat dikurangi tanpa interpolasi:
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
Mengubah bentuk array, kami mendapat 2 sumbu baru, 2 nilai di masing-masing, mereka sesuai dengan bingkai yang terdiri dari baris dan kolom ganjil dan genap dari gambar asli.
Kualitas yang buruk disebabkan oleh penggunaan Matplotlib, karena di sana Anda dapat melihat dimensi aksial. Faktanya, kualitas gambar mini adalah:
<up>Penataan ulang dan transposisi sumbu
Selain mengubah bentuk array dengan urutan unit data yang sama, sering kali perlu mengubah urutan sumbu, yang secara alami akan memerlukan permutasi blok data.
Contoh dari transformasi semacam itu adalah transposisi dari sebuah matriks: mempertukarkan baris dan kolom.
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
Dalam contoh ini, konstruk AT digunakan untuk mengubah posisi matriks A. Operator transpos membalikkan urutan sumbu. Pertimbangkan contoh lain dengan tiga sumbu:
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
Entri singkat ini memiliki mitra yang lebih panjang: np.transpose (A). Ini adalah alat yang lebih fleksibel untuk mengganti urutan sumbu. Parameter kedua memungkinkan Anda untuk menentukan tupel nomor sumbu dari array sumber, yang menentukan urutan posisi mereka dalam array yang dihasilkan.
Misalnya, mengatur ulang dua sumbu pertama gambar. Gambar harus dibalik, tetapi biarkan sumbu warna tidak berubah:
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
Untuk contoh ini, alat swapax lain dapat digunakan. Metode ini menukar dua sumbu yang ditentukan dalam parameter. Contoh di atas dapat diimplementasikan seperti ini:
I_ = np.swapaxes(I, 0, 1)
<up>Array bergabung
Array yang digabung harus memiliki jumlah sumbu yang sama. Array dapat dikombinasikan dengan pembentukan sumbu baru, atau sepanjang yang sudah ada.
Untuk menggabungkan dengan pembentukan sumbu baru, array asli harus memiliki dimensi yang sama di sepanjang semua sumbu:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
Seperti yang Anda lihat dari contoh, array operan menjadi subarrays dari objek baru dan berbaris di sepanjang sumbu baru, yang merupakan urutan pertama.
Untuk menggabungkan array di sepanjang sumbu yang ada, mereka harus memiliki ukuran yang sama pada semua sumbu kecuali yang dipilih untuk bergabung, dan mereka dapat memiliki ukuran sewenang-wenang di sepanjang itu:
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
Untuk menggabungkan sepanjang sumbu pertama atau kedua, Anda dapat menggunakan metode vstack dan hstack. Kami menunjukkan ini dengan contoh gambar. vstack menggabungkan gambar dengan lebar yang sama tingginya, dan hsstack menggabungkan gambar dengan tinggi yang sama dalam satu lebar:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
Harap dicatat bahwa dalam semua contoh bagian ini, array yang bergabung dilewatkan oleh satu parameter (tuple). Jumlah operan bisa berapa saja, tetapi tidak harus hanya 2.
Perhatikan juga apa yang terjadi pada memori saat menggabungkan array:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
Karena objek baru dibuat, data di dalamnya disalin dari array asli, sehingga perubahan dalam data baru tidak mempengaruhi yang asli.
<up>Kloning data
Operator np.repeat (A, n) akan mengembalikan array satu dimensi dengan elemen array A, yang masing-masing akan diulang n kali.
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
Setelah konversi ini, Anda dapat membangun kembali geometri array dan mengumpulkan data duplikat dalam satu sumbu:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
Opsi ini berbeda dari menggabungkan array dengan operator stack itu sendiri hanya pada posisi sumbu di mana data yang sama berada. Pada contoh di atas, ini adalah sumbu terakhir, jika Anda menggunakan tumpukan - yang pertama:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
Tidak peduli bagaimana data dikloning, langkah selanjutnya adalah memindahkan sumbu yang nilainya sama dengan posisi apa pun dengan sistem sumbu:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
Jika kita ingin "meregangkan" sumbu apa pun menggunakan pengulangan elemen, maka sumbu dengan nilai yang sama harus diletakkan
setelah diperluas (menggunakan transpose), dan kemudian menggabungkan kedua sumbu ini (menggunakan membentuk kembali). Pertimbangkan contoh dengan merentangkan gambar di sepanjang sumbu vertikal dengan menduplikasi baris:
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<up>Operasi matematika pada elemen array
Jika A dan B adalah array dengan ukuran yang sama, maka mereka dapat ditambahkan, dikalikan, dikurangi, dibagi dan dinaikkan ke daya. Operasi ini dilakukan berdasarkan
elemen , array yang dihasilkan akan bertepatan dalam geometri dengan array asli, dan setiap elemen akan menjadi hasil dari operasi yang sesuai pada sepasang elemen dari array asli:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
Anda dapat melakukan operasi apa pun dari atas pada array dan angka. Dalam hal ini, operasi juga akan dilakukan pada masing-masing elemen array:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
Mempertimbangkan bahwa array multidimensi dapat dianggap sebagai array datar (sumbu pertama), yang elemennya adalah array (sumbu lain), dimungkinkan untuk melakukan operasi yang dipertimbangkan pada array A dan B dalam kasus ketika geometri B bertepatan dengan geometri dari sub-array A dengan nilai tetap sepanjang sumbu pertama . Dengan kata lain, dengan jumlah sumbu dan ukuran yang sama A [i] dan B. Dalam hal ini, masing-masing array A [i] dan B akan operan untuk operasi yang didefinisikan pada array.
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
Dalam contoh ini, array B dikenai operasi dengan setiap deretan array A. Jika Anda perlu melipatgandakan / membagi / menambah / mengurangi / menaikkan derajat subarrays di sepanjang sumbu lain, Anda perlu menggunakan transposisi untuk meletakkan sumbu yang diinginkan di tempat pertama, dan kemudian mengembalikannya ke tempatnya. Perhatikan contoh di atas, tetapi dengan perkalian dengan vektor B dari kolom array A:
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
(, , , , , , ..) NumPy . :
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
NumPy
.
<>. dot(A, B). , :
- (), ;
- ( ) , ;
- jika argumennya adalah vektor, maka perkalian skalar akan dilakukan (jumlah produk elemen-bijaksana);
- jika argumennya adalah tensor (array multidimensi) dan skalar, maka vektor akan dikalikan dengan angka;
- jika argumen tensor, maka produk tensor sepanjang sumbu terakhir dari argumen pertama dan kedua dari belakang akan dieksekusi;
- jika argumennya adalah matriks, maka produk dari matriks dieksekusi (ini adalah kasus khusus dari produk tensor);
- jika argumennya adalah matriks dan vektor, maka produk dari matriks dan vektor akan dieksekusi (ini juga merupakan kasus khusus dari produk tensor).
Untuk melakukan operasi, ukuran yang sesuai harus bertepatan: untuk vektor panjang, untuk tensor, panjang di sepanjang sumbu di mana produk elemen-bijaksana akan dijumlahkan.Pertimbangkan contoh dengan skalar dan vektor:
Dengan tensor, kita hanya akan melihat bagaimana geometri array yang dihasilkan berubah ukuran:
Untuk melakukan produk tensor menggunakan sumbu lain, alih-alih yang ditentukan untuk titik, Anda dapat menggunakan tensordot dengan sumbu eksplisit: A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
Kami telah secara eksplisit menunjukkan bahwa kami menggunakan sumbu ketiga dari array pertama dan kedua - dari yang kedua (ukuran di sepanjang sumbu ini harus cocok).<up>Agregator
Agregator adalah metode NumPy yang memungkinkan Anda untuk mengganti data dengan karakteristik integral sepanjang beberapa sumbu. Misalnya, Anda dapat menghitung nilai rata-rata, maksimum, minimum, variasi, atau karakteristik lain di sepanjang sumbu atau sumbu apa pun dan membentuk array baru dari data ini. Bentuk array baru akan berisi semua sumbu dari array asli, kecuali yang sepanjang agregator dihitung.Sebagai contoh, kita akan membentuk array dengan nilai acak. Kemudian kami menemukan nilai minimum, maksimum, dan rata-rata di kolomnya: A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
Dengan penggunaan ini, rata - rata dan rata - rata terlihat seperti sinonim. Tetapi fungsi-fungsi ini memiliki serangkaian parameter tambahan yang berbeda. Ada berbagai kemungkinan untuk menutupi dan menimbang data rata-rata.Anda dapat menghitung karakteristik integral dalam beberapa sumbu: A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
Dalam contoh ini, jumlah karakteristik integral lainnya dipertimbangkan - jumlahnya.Daftar agregator terlihat seperti ini:- jumlah: jumlah dan nansum - varian yang benar mengelola dengan nan;
- kerja: prod dan nanprod;
- rata-rata dan harapan: rata-rata dan rata-rata (nanmean),
tidak ada pengurangan ; - median: median dan nanmedian;
- persentil: persentil dan nanpercentile;
- variasi: var dan nanvar;
- standar deviasi (akar kuadrat variasi): std dan nanstd;
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
argmin argmax (, nanargmin, nanargmax) , .
,
. argmin argmax , - ravel().
, NumPy, : np.aggregator(A, axes) A.aggregator(axes), aggregator , axes — .
A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<>—
Mari kita membangun algoritma untuk penyaringan gambar low-pass linier.Untuk memulai, unggah gambar yang berisik.
Pertimbangkan fragmen gambar untuk melihat noise:
Kami akan memfilter gambar menggunakan filter Gaussian. Tetapi alih-alih melakukan konvolusi secara langsung (dengan iterasi), kami menerapkan rata-rata tertimbang dari irisan gambar yang bergeser relatif satu sama lain: def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
Kami menerapkan fungsi ini ke gambar kami sekali, dua kali dan tiga kali: I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
Kami mendapatkan hasil berikut:
dengan sekali pakai filter;
dengan ganda;
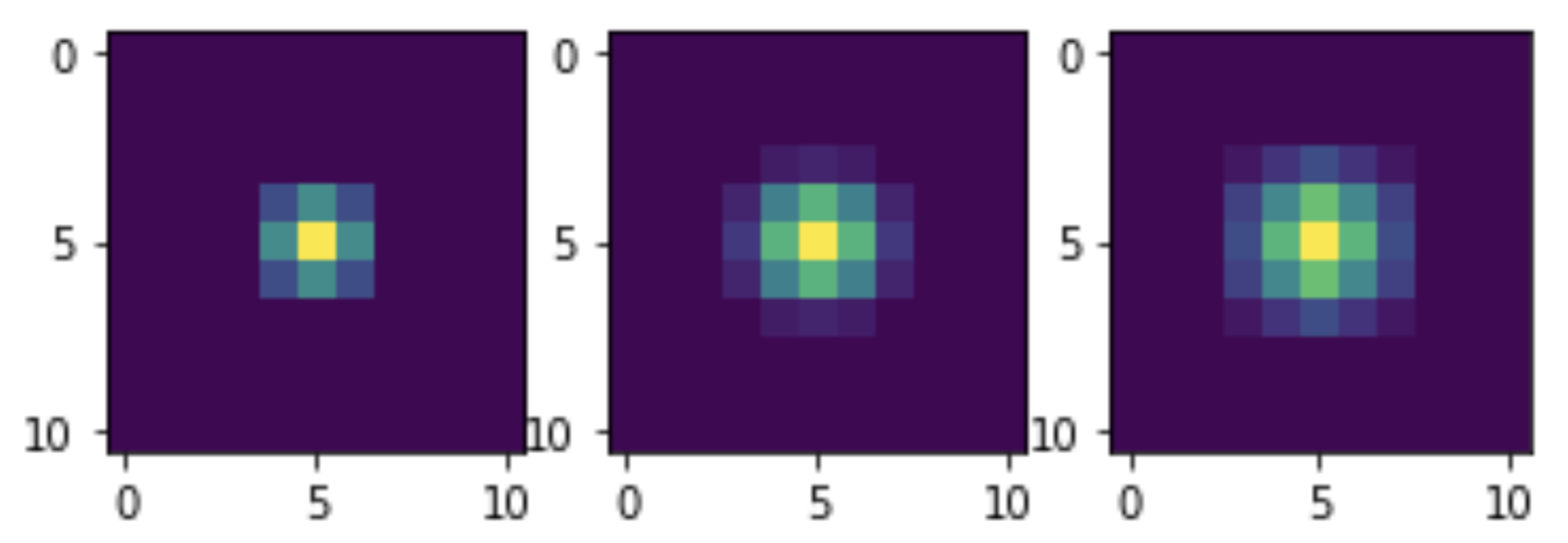
tiga kali.Dapat dilihat bahwa dengan peningkatan jumlah lintasan filter, tingkat kebisingan berkurang. Namun ini juga mengurangi kejernihan gambar. Ini adalah masalah yang diketahui dengan filter linear. Tetapi metode denoising gambar kami tidak mengklaim sebagai yang optimal: ini hanya demonstrasi kemampuan NumPy untuk mengimplementasikan konvolusi tanpa iterasi.Sekarang mari kita lihat konvolusi dengan kernel mana filter kita setara. Untuk melakukan ini, kita akan tunduk pada satu unit impuls untuk transformasi yang sama dan memvisualisasikan. Bahkan, impuls tidak akan tunggal, tetapi sama dalam amplitudo ke 255, karena pencampuran itu sendiri dioptimalkan untuk data integer. Tapi ini tidak mengganggu menilai penampilan umum inti: M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
Kami menganggap jauh dari rangkaian lengkap fitur NumPy, saya harap ini cukup untuk menunjukkan kekuatan penuh dan keindahan alat ini!<up>