Baru-baru ini, sebuah artikel dengan judul yang tidak begitu menarik, "
reparameterisasi saraf meningkatkan optimasi struktural ", diunggah ke arXiv.org [arXiv: 1909.04240]. Namun, ternyata penulis, pada kenyataannya, datang dengan dan menggambarkan metode yang sangat sepele menggunakan jaringan saraf untuk mendapatkan solusi untuk masalah struktural / optimasi topologi model fisik (meskipun penulis sendiri mengatakan bahwa metode ini lebih universal). Pendekatan ini sangat ingin tahu, produktif, dan tampaknya benar-benar baru (namun, saya tidak dapat menjamin yang terakhir, tetapi baik penulis karya, maupun komunitas ODS, atau saya tidak dapat mengingat analog), jadi mungkin berguna untuk mengetahui bagi mereka yang tertarik menggunakan jaringan saraf, serta menyelesaikan berbagai masalah optimasi.
Apa yang kamu bicarakan Apa tugas optimasi topologi?
Bayangkan saja apa yang Anda butuhkan, misalnya, untuk mendesain seutas jembatan, gedung bertingkat, sayap pesawat terbang, bilah turbin, atau apa pun. Biasanya, ini diselesaikan dengan mencari spesialis, misalnya, seorang arsitek yang, menggunakan pengetahuannya tentang matan, sopromat, area target, serta pengalaman, intuisi, tata letak tes, dll. dll. akan membuat proyek yang diinginkan. Penting di sini bahwa proyek yang diterima ini hanya baik untuk yang terbaik dari spesialis ini. Dan ini, tentu saja, tidak selalu cukup. Oleh karena itu, ketika komputer menjadi cukup kuat, kami mulai mencoba mengalihkan tugas seperti itu kepada mereka. Karena
jelas apa yang dapat disimpan komputer dalam memori dan hubungan pendek ... mengapa tidak?
Tugas semacam itu disebut "masalah optimisasi struktural", yaitu menghasilkan desain yang optimal dari struktur mekanik penahan beban [1]. Subbagian dari masalah pengoptimalan struktural adalah masalah pengoptimalan
topologis (pada kenyataannya, pekerjaan yang dimaksud secara khusus difokuskan pada mereka, tetapi ini sama sekali bukan intinya, dan lebih banyak tentang itu nanti) Masalah optimisasi topologi tipikal terlihat seperti ini: untuk konsep tertentu (jembatan, rumah, dll.) Di ruang dalam dua atau tiga dimensi, memiliki batasan spesifik dalam bentuk bahan, teknologi, dan persyaratan lain, memiliki beberapa beban eksternal, Anda perlu merancang Struktur optimal yang akan menahan beban dan memenuhi kendala.
- "Merancang" pada dasarnya berarti menemukan / menggambarkan ruang bagian dari ruang sumber yang perlu diisi dengan bahan bangunan.
- Optimalitas dapat dinyatakan, misalnya, dalam bentuk persyaratan untuk meminimalkan berat total struktur dalam pembatasan dalam bentuk tegangan maksimum yang diijinkan dalam material dan kemungkinan perpindahan pada beban yang diberikan.
Untuk mengatasi masalah ini di komputer, ruang solusi target disampel menjadi satu set elemen hingga (piksel untuk 2D dan voxels untuk 3D) dan kemudian, menggunakan beberapa algoritma, komputer memutuskan apakah akan mengisi elemen individual ini dengan materi atau membiarkannya kosong?

(Gambar dari "Perkembangan dalam Topologi dan Optimasi Bentuk", Chau Hoai Le, 2010)
Jadi, sudah dari pernyataan masalah jelas bahwa solusinya cukup besar bagi para ilmuwan. Saya dapat menawarkan kepada mereka yang menginginkan beberapa perincian, misalnya, melihat yang sangat lama (2010, yang masih banyak untuk bidang yang sedang berkembang aktif), tetapi disertasi Chau Hoai Le yang cukup terperinci dan mudah dicari berjudul "Perkembangan dalam Topologi dan Optimasi Bentuk" [2], dari mana Saya mencuri gambar atas dan bawah.
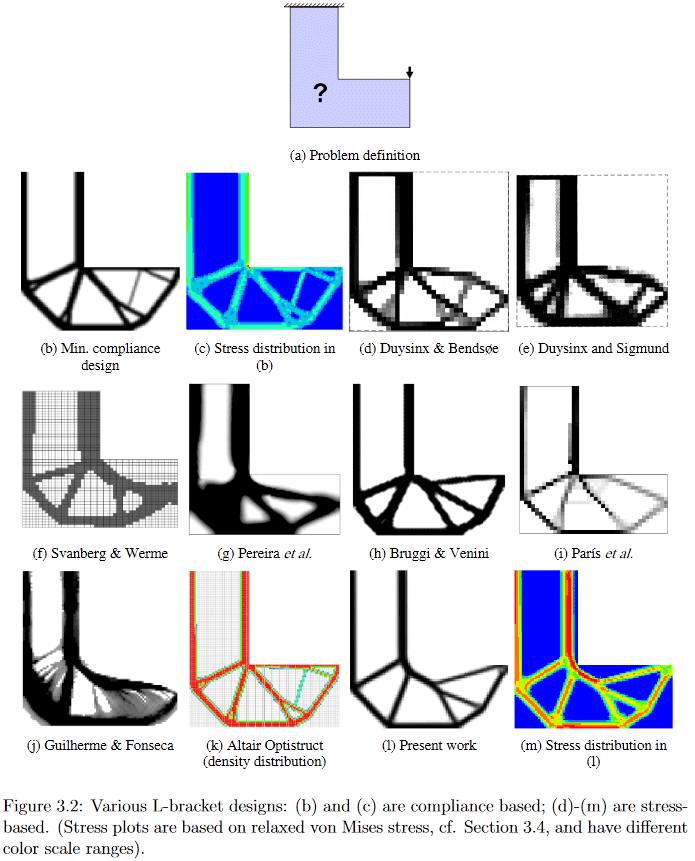
(Gambar dari "Perkembangan dalam Topologi dan Optimasi Bentuk", Chau Hoai Le, 2010)
Sebagai contoh, dalam gambar ini Anda dapat dengan jelas melihat bagaimana algoritma yang sangat berbeda menghasilkan solusi untuk masalah desain yang tampaknya sederhana dari suspensi berbentuk L.
Jadi, sekarang kembali ke pekerjaan yang dimaksud.
Para penulis sangat cerdas menyarankan pemecahan masalah optimasi tersebut dengan menghasilkan solusi kandidat oleh jaringan saraf dan evolusi selanjutnya dari solusi dengan metode gradient descent sehubungan dengan fungsi kepatuhan objektif. Kesesuaian struktur yang dihasilkan diperkirakan menggunakan model fisik yang dapat dibedakan, yang, pada kenyataannya, memungkinkan penggunaan gradient descent. Menurut mereka (penulis menerbitkan
kode sumber [5]), ini memberikan hasil yang sama dengan algoritma tradisional terbaik untuk masalah sederhana, atau yang terbaik dari algoritma ini digunakan sebagai baseline, untuk yang kompleks.
Metode
Selanjutnya saya akan mencoba untuk menggambarkan apa dan bagaimana tepatnya yang diusulkan penulis untuk dilakukan, tetapi saya segera memperingatkan bahwa saya tidak menjamin kebenaran 100%, karena selain pengetahuan saya yang sangat berkarat di lapangan, saya harus menambahkan, di samping singkatnya deskripsi yang sangat sedikit, beberapa “ketidakdewasaan” yang umum dari artikel tersebut, yang, dilihat dari kehadiran dua edisi dalam 4 hari, sedang diselesaikan (
ditambahkan: saat ini, saya percaya bahwa, setidaknya, pada dasarnya, semuanya dijelaskan dengan benar).
Para penulis, secara umum, mengikuti pendekatan untuk menyelesaikan masalah optimasi tersebut, yang disebut "metode SIMP yang dimodifikasi", dan dijelaskan secara rinci dalam [3] "Optimalisasi topologi yang efisien dalam MATLAB menggunakan 88 baris kode". Pracetak dari karya ini dan kode yang terkait dengannya dapat ditemukan di
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in-MATLAB . Pekerjaan ini sering digunakan untuk mulai mengajar siswa tentang masalah optimasi topologi, oleh karena itu, untuk lebih memahaminya, disarankan untuk terbiasa dengannya.
Dalam "SIMP yang dimodifikasi", solusinya dioptimalkan secara langsung dengan memodifikasi piksel gambar kepadatan fisik. Para penulis makalah tidak mengusulkan untuk memodifikasi gambar secara langsung (meskipun algoritma seperti itu, dengan hal-hal lain dianggap sama, adalah yang kontrol), tetapi untuk mengubah parameter dan input dari jaringan saraf convolutional yang menghasilkan gambar kepadatan fisik. Begini cara keseluruhan metode terlihat secara global:

(Gambar dari publikasi yang dimaksud)
Langkah 1, menghasilkan kandidat
Jaringan saraf (selanjutnya disebut sebagai NS) menggunakan vektor input primer acak _beta (itu, seperti bobot jaringan, adalah parameter terlatih), menghasilkan (beberapa) gambar solusi (bekerja dengan 2D, tetapi dalam 3D, saya pikir, dapat juga didistribusikan ) Bagian upampling dari arsitektur U-Net yang terkenal digunakan sebagai generator NS.
Langkah 2, menerapkan pembatasan dan mengubah kandidat menjadi kerangka model fisik
Nilai piksel dikonversi ke kepadatan fisik dalam dua langkah:
- Pertama, dalam satu langkah, masalah normalisasi nilai-nilai non-normal dari piksel yang dihasilkan diselesaikan (NS dirancang sehingga menghasilkan apa yang disebut log - nilai dalam kisaran (-inf, + inf)) dan menerapkan batasan pada jumlah total solusi yang dihasilkan. Untuk ini, sigmoid diterapkan elemen-bijaksana pada gambar, argumen yang digeser oleh konstanta tergantung pada gambar yang ditransformasikan dan volume solusi yang diinginkan (nilai konstanta bias ini dipilih oleh pencarian biner sehingga total volume kepadatan yang diperoleh akan sama dengan volume yang telah ditentukan sebelumnya. V0). Analisis terperinci dari tahap ini, lihat komentar );
- Selanjutnya, gambar yang dinormalisasi dari kepadatan struktur diproses oleh apa yang disebut filter kerapatan dengan jari-jari 2. Dalam istilah yang lebih dikenal, filter ini tidak lebih dari rata-rata tertimbang normal dari titik-titik tetangga dalam gambar. Bobot dalam filter ini (inti filter) dapat direpresentasikan sebagai nilai ketinggian titik yang terletak di permukaan kerucut biasa yang terletak di bidang sehingga verteksnya berada pada titik saat ini, oleh karena itu penulis menyebutnya filter kerucut (lebih lanjut tentang topik ini lihat deskripsi filter densitas pada bab 2.3. Penyaringan [3]).
Singkatnya, inti dari seluruh langkah 2 adalah bahwa keluaran NS yang tidak normal sepenuhnya berubah menjadi kerangka model fisik yang dinormalisasi dan sedikit dihaluskan (seperangkat kepadatan elemen fisik), yang telah diterapkan pembatasan apriori yang diperlukan (ini adalah jumlah bahan yang digunakan).
Langkah 3, evaluasi model fisik kerangka yang dihasilkan
Kerangka kerja yang dihasilkan dijalankan melalui mesin fisik yang dapat dibedakan untuk mendapatkan vektor (/ tensor?) Dari perpindahan struktural di bawah beban (termasuk gravitasi) U. Kuncinya di sini adalah diferensiabilitas mesin, yang memungkinkan kita untuk mendapatkan gradien (saya ingat bahwa gradien fungsi umumnya tensor terdiri dari turunan parsial dari suatu fungsi sehubungan dengan semua argumennya. Gradien menunjukkan arah dan laju perubahan fungsi pada titik saat ini, oleh karena itu, dengan mengetahuinya, Anda dapat "memutar" argumen sehingga perubahan yang diinginkan terjadi dengan fungsi tersebut - berkurang atau bertambah). Mesin fisik yang dapat dibedakan seperti itu tidak perlu ditulis dari awal - mereka sudah lama ada dan sudah dikenal luas. Penulis hanya perlu melakukan pairing dengan paket perhitungan jaringan saraf, seperti TensorFlow / PyTorch.
Langkah 4, menghitung nilai fungsi obyektif untuk bingkai gambar / kandidat
Fungsi tujuan skalar c (x) yang akan diperkecil dihitung, yang menggambarkan kepatuhan (itu adalah kebalikan dari kekakuan) dari kerangka kerja yang dihasilkan. Fungsi kepatuhan tergantung pada vektor shift U yang diperoleh pada langkah terakhir dan matriks kekakuan struktur K (Saya tidak memiliki cukup pengetahuan tentang optimasi topologi untuk memahami dari mana K berasal - saya akan menganggap bahwa itu tampaknya langsung dipertimbangkan dari kerangka kerja).
/ *
lihat juga komentar
(1) dari
kxx dan
(2) dari
350 Stealth , meskipun pencerahan dasar layak untuk digunakan [3].
* /
Dan kemudian selesai. Karena semuanya dibuat dalam lingkungan dengan diferensiasi otomatis, pada tahap ini kita secara otomatis mendapatkan semua gradien dari fungsi tujuan, yang didorong karena diferensiabilitas semua transformasi pada setiap langkah kembali ke bobot dan vektor input dari jaringan saraf pembangkit. Bobot dan vektor input, masing-masing, dengan turunan parsialnya, berubah, menyebabkan perubahan yang diperlukan - meminimalkan fungsi tujuan. Selanjutnya, siklus baru lintasan langsung melalui NS terjadi -> aplikasi pembatasan -> perhitungan model fisik -> perhitungan fungsi tujuan -> gradien baru dan memperbarui bobot. Demikian seterusnya hingga konvergensi Algo.
Poin penting, deskripsi yang saya tidak temukan dalam pekerjaan, adalah bagaimana volume total konstruksi V0 dipilih, dengan bantuan yang solusi kandidat dikonversi ke kerangka kerja pada langkah 2. Jelas, sifat-sifat solusi yang dihasilkan sangat tergantung pada pilihannya. Dengan indikasi tidak langsung (semua contoh solusi yang diperoleh [4] memiliki beberapa contoh berbeda persis dalam batasan volume), saya berasumsi bahwa mereka hanya memperbaiki V0 pada grid tertentu dari kisaran [0,05, 0,5] dan kemudian mereka melihat solusi yang diperoleh dengan mata yang berbeda V0. Nah, untuk pekerjaan konseptual, ini, secara umum, sudah cukup, meskipun, tentu saja, akan sangat menarik untuk melihat opsi dengan pemilihan V0 ini juga, tetapi, itu mungkin akan pergi ke tahap pengembangan pekerjaan selanjutnya.
Poin penting kedua, yang saya tidak mengerti, adalah bagaimana mereka memberlakukan batasan / persyaratan pada jenis solusi tertentu. Yaitu jika Anda masih dapat memisahkan jembatan dari bangunan berkat model fisik (bangunan memiliki dukungan penuh, dan jembatan hanya di ujung perbatasan), lalu bagaimana cara memisahkan, katakanlah, bangunan 3 lantai dari bangunan 4 lantai?
Bagaimana cara kerjanya?
Ternyata untuk masalah kecil (dalam hal ukuran ruang solusi = jumlah piksel), metode tersebut memberikan ± kualitas hasil yang sama dengan metode tradisional terbaik untuk optimasi topologi, tetapi pada yang besar (ukuran grid dari 2 ^ 15 atau lebih piksel, mis. , misalnya, dari 128 * 256 dan lebih banyak) memperoleh solusi berkualitas tinggi dengan metode ini lebih mungkin daripada yang tradisional terbaik (dari 116 masalah yang diuji, metode ini memberikan solusi yang disukai dalam 99 masalah, dibandingkan dengan 66 yang disukai dalam yang tradisional terbaik).
Terlebih lagi, di sini sesuatu yang sangat menarik dimulai. Metode tradisional optimasi topologi dalam masalah besar menderita dari kenyataan bahwa pada tahap awal pekerjaan mereka dengan cepat membentuk web skala kecil, yang kemudian mengganggu pengembangan struktur skala besar. Ini mengarah pada fakta bahwa hasil yang diperoleh sulit / tidak mungkin untuk diimplementasikan secara fisik. Oleh karena itu, secara paksa ada satu arah dalam masalah optimisasi topologi yang mempelajari / menghasilkan metode bagaimana membuat solusi yang dihasilkan lebih nyaman secara teknologi.
Di sini, tampaknya, berkat jaringan konvolusi, optimisasi terjadi secara bersamaan pada beberapa skala spasial pada saat yang sama, yang memungkinkan untuk menghindari / sangat mengurangi "web" dan mendapatkan solusi yang lebih sederhana, namun berkualitas tinggi dan ramah teknologi!
Selain itu, sekali lagi berkat konvolusi jaringan, solusi yang berbeda secara fundamental diperoleh daripada metode standar-tradisional.
Misalnya, dalam desain:
- metode balok kantilever menemukan solusi hanya 8 komponen, sedangkan tradisional terbaik - 18.
- Metode dukungan jembatan tipis memilih satu dukungan dengan pola percabangan seperti pohon, sedangkan yang tradisional - dua dukungan
- Metode atap menggunakan kolom, sedangkan metode tradisional menggunakan pola percabangan. Dll
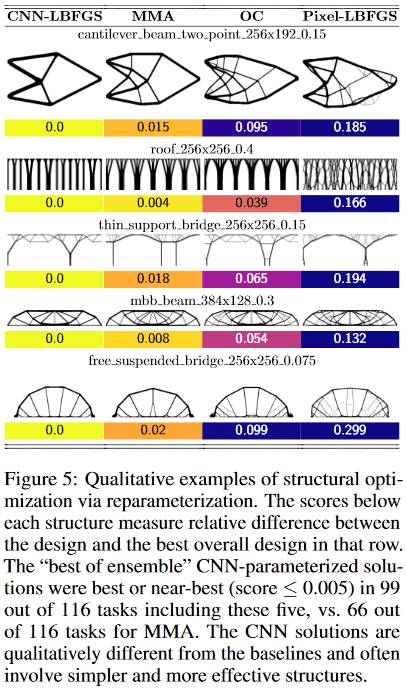
(Gambar dari publikasi yang dimaksud)
Apa yang istimewa dari pekerjaan ini?
Saya belum pernah melihat penggunaan jaringan saraf seperti itu. Biasanya, jaringan saraf digunakan untuk mendapatkan beberapa fungsi yang sangat rumit dan kompleks y = F (x, theta) (di mana x adalah argumen, dan theta adalah parameter khusus), yang dapat melakukan sesuatu yang bermanfaat. Misalnya, jika x adalah gambar dari kamera mobil, maka nilai fungsi tersebut dapat, misalnya, tanda apakah ada pejalan kaki di dekat mobil yang berbahaya. Yaitu penting di sini bahwa jenis fungsi itu sendiri, yang berulang kali digunakan untuk menyelesaikan suatu masalah, berharga.
Di sini, jaringan saraf digunakan sebagai peniru repositori-modifier-adjuster parameter dari beberapa model fisik, yang, karena arsitekturnya, memberlakukan batasan tertentu pada nilai dan variasi perubahan dalam parameter ini (pada kenyataannya, contoh di bawah judul Pixel-LBFGS adalah upaya untuk mengoptimalkan piksel secara langsung, bukan menggunakan jaringan saraf untuk menghasilkan mereka, hasilnya terlihat, NS penting). Di sinilah konvolusi jaringan saraf yang digunakan menjadi sangat penting, karena arsitekturnya yang memungkinkan Anda untuk "menangkap" konsep invarian transfer dan sedikit rotasi (bayangkan Anda mengenali teks dari gambar - penting bagi Anda untuk mengekstrak teks dan tidak masalah yang mana bagian dari gambar, itu terletak dan bagaimana itu diputar - yaitu, Anda perlu invarian transfer dan rotasi). Dalam masalah ini, beberapa jenis tongkat fisik, yang merupakan unit struktur dan banyak yang kami optimalkan, masih tetap terlepas dari posisi dan orientasinya di ruang.
Jaringan klasik yang sepenuhnya terhubung, misalnya, mungkin tidak akan berfungsi di sini (sama baiknya), karena arsitekturnya memungkinkan terlalu banyak / kecil (well, ya, dualisme seperti itu, bagaimana cara melihatnya). Pada saat yang sama, meskipun fakta bahwa NS tetap di sini fungsi yang sangat rumit dan rumit y = F (x, theta), dalam tugas ini kita akhirnya tidak peduli dengan argumennya x atau parameternya theta , dan bagaimana fungsi akan digunakan. Kami hanya memperhatikan nilai tunggal y, yang diperoleh dalam proses mengoptimalkan satu fungsi objektif spesifik untuk satu model fisik tertentu, di mana {x, theta} hanyalah parameter yang dapat dikonfigurasi!
Menurut saya ini ide yang sangat keren dan baru! (walaupun, tentu saja, kemudian, seperti biasa, mungkin ternyata Schmidhuber menggambarkannya kembali di awal tahun 90-an, tetapi kita akan menunggu dan melihat)
Secara umum, makna metode ini agak mengingatkan pada pembelajaran yang diperkuat - di sana NS digunakan, secara kasar, sebagai "gudang pengalaman" dari agen yang bertindak dalam lingkungan tertentu, yang diperbarui saat lingkungan menerima umpan balik atas tindakan agen. Hanya di sana, "repositori pengalaman" yang sangat ini terus digunakan untuk membuat keputusan baru oleh agen, dan di sini hanya repositori parameter model fisik, dari mana kami hanya tertarik pada satu-satunya hasil akhir dari optimasi.
Nah, yang terakhir. Saat yang menarik menarik perhatian saya.
Beginilah solusi optimal untuk tugas bangunan bertingkat seperti:
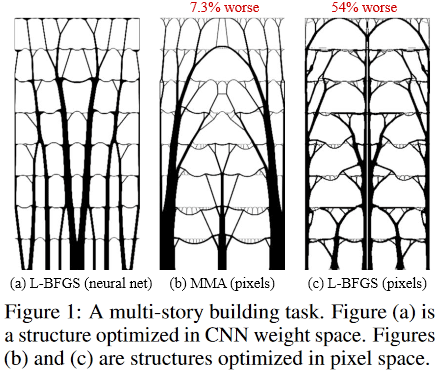
(Gambar dari publikasi yang dimaksud)
Jadi:

terletak di dalam Sagrada Familia yang fantastis, Kuil Keluarga Suci, yang terletak di Barcelona, Spanyol, yang “dirancang” oleh Antonio Gaudi yang brilian.
Ucapan Terima Kasih
Saya berterima kasih kepada penulis pertama artikel tersebut, Stephan Hoyer, untuk bantuan yang cepat dalam mengklarifikasi beberapa detail pekerjaan yang tidak jelas, serta para peserta Habr yang membuat tambahan dan / atau ide-ide provokatif yang berguna.
[1]
opsi untuk menentukan masalah optimasi struktural / topologi[2]
"Perkembangan dalam Topologi dan Optimalisasi Bentuk"[3] Andreassen, E., Clausen, A., Schevenels, M., Lazarov, BS, dan Sigmund, O. Optimalisasi topologi yang efisien dalam MATLAB menggunakan 88 baris kode. Optimalisasi Struktural dan Multidisipliner, 43 (1): 1–16, 2011. Cetakan awal dari pekerjaan dan kode ini tersedia di
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in -MATLAB[4]
contoh solusi kerja[5] Kode sumber pekerjaan:
https://github.com/google-research/neural-structural-optimization
Lihat juga
Pembaruan terakhir dari publikasi ini 2020.01.23 09:18