Saya menemukan sebuah teka-teki yang menarik: Memang, angka a dan bilangan positif n diberikan. Hitung akar n angka tanpa menggunakan pustaka.
Input data: angka a adalah nyata, non-negatif, tidak melebihi 1000, ditentukan dengan akurasi 6 desimal. Angka n adalah alami, tidak melebihi 10.
Keluaran: Program harus menampilkan satu angka: jawaban untuk masalah dengan akurasi setidaknya 5 desimal.
Tentu saja, menarik untuk menyelesaikannya dalam konsep dengan pensil, dan kemudian menggambarnya di editor dan mencoba untuk mengkompilasinya. Tanpa googling, kiat dan bahkan lebih banyak lagi menggunakan perpustakaan. Jika Anda memutuskan ini untuk pertama kalinya, maka pertama-tama cobalah menulis sebuah program untuk menemukan akar kuadrat yang biasa. Jika Anda menemukan tugas yang sulit, selesaikan hampir sama, tetapi lebih sederhana. Maka rasa takut Anda akan hilang dan semacam pemahaman kasar akan muncul.
Jadi sebagai permulaan, saya akan memberikan contoh cara menghitung akar kuadrat tanpa menggunakan fungsi pustaka. Algoritma Iterasi Berurutan. Konvergen cukup cepat bahkan untuk jumlah besar.
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
Anda dapat menjalankan kode di sini:
KLIKKompleksitas logaritmik dari algoritma? Atau yang lain? :)
Sekarang Anda dapat beralih ke versi tugas yang rumit. Dalam hal ini, solusinya lebih digeneralisasi.
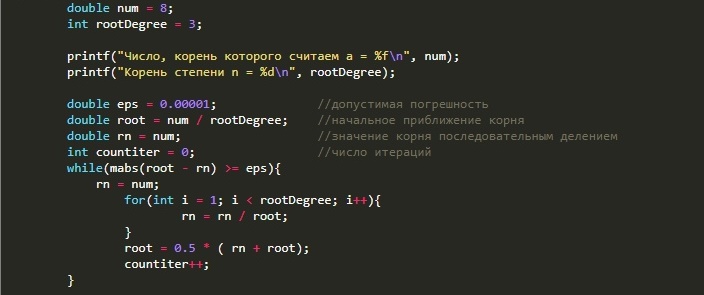
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
Anda dapat menjalankan kode di sini:
KLIKDalam solusi ini, saya menggunakan ide perkiraan awal yang relatif baik. Kemudian pembagian sekuensial adalah perkiraan kedua dari akar tingkat ke-n. Selanjutnya, perkiraan baru dipertimbangkan dengan rata-rata dua yang sekarang. Secara konsisten, algoritma menyatu ke root yang diinginkan dengan kesalahan yang telah ditentukan. Ini agak seperti metode iterasi sederhana.
Ini adalah algoritma kerja pertama yang ditulis di lutut. Kita masih perlu merefleksikan kompleksitas dan kemungkinan akselerasi. Omong-omong, fitur akselerasi apa dari algoritma ini yang dapat diterapkan menurut Anda?
Saya merasa bahwa akan ada pertanyaan: "Mengapa melakukan ini jika semuanya diterapkan di perpustakaan seratus tahun yang lalu?!"
Jawab: Secara pribadi, saya selalu suka berpikir tentang algoritma yang sudah diterapkan di perpustakaan standar. Cobalah untuk mengembangkannya sendiri (baik, atau untuk mengembangkan semacam parodi yang bergerak lambat dan gagal). Ini melatih otak dengan sangat baik. Karena itu, menurut saya, “reinventing the wheel” sangat berguna. Dan sangat berbahaya untuk selalu menggunakan segala sesuatu yang sudah siap, tanpa mengetahui struktur internal.