Oh metode Newton ini

Banyak yang telah ditulis tentang metode optimasi numerik. Ini dapat dimengerti, terutama dengan latar belakang keberhasilan yang baru-baru ini ditunjukkan oleh jaringan saraf yang dalam. Dan sangat memuaskan bahwa setidaknya beberapa penggemar tertarik tidak hanya pada bagaimana membom jaringan saraf mereka pada kerangka kerja yang telah mendapatkan popularitas di Internet ini, tetapi juga bagaimana dan mengapa semuanya bekerja. Namun, saya baru-baru ini harus mencatat bahwa dalam mengajukan masalah yang berkaitan dengan pelatihan jaringan saraf (dan tidak hanya dengan pelatihan, dan tidak hanya jaringan), termasuk di Habré, semakin sering sejumlah pernyataan "terkenal" digunakan untuk penerusan, validitasnya secara halus, diragukan. Di antara pernyataan meragukan tersebut:

1. Metode pesanan kedua dan lebih banyak tidak berfungsi dengan baik dalam tugas-tugas pelatihan jaringan saraf. Karena itu.
2. Metode Newton membutuhkan kepastian positif dari matriks Hessian (turunan kedua) dan karenanya tidak bekerja dengan baik.
   
3. Metode Levenberg-Marquardt adalah kompromi antara gradient descent dan metode Newton dan umumnya heuristik.
   

dll. Daripada melanjutkan daftar ini, lebih baik turun ke bisnis. Dalam posting ini kita akan mempertimbangkan pernyataan kedua, karena saya hanya bertemu dengannya setidaknya dua kali di Habré. Saya akan menyentuh pada pertanyaan pertama hanya pada bagian mengenai metode Newton, karena jauh lebih luas. Yang ketiga dan sisanya akan dibiarkan sampai waktu yang lebih baik.

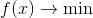
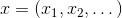
Fokus perhatian kami adalah tugas optimasi tanpa syarat dimana - titik ruang vektor, atau hanya - vektor. Secara alami, tugas ini lebih mudah untuk diselesaikan, semakin banyak yang kita ketahui . Biasanya diasumsikan dapat dibedakan sehubungan dengan setiap argumen , dan sebanyak yang diperlukan untuk perbuatan kotor kita. 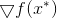Sudah diketahui bahwa kondisi yang diperlukan untuk itu pada suatu titik minimum tercapai, adalah kesetaraan gradien fungsi pada titik ini nol. Dari sini kita langsung mendapatkan metode minimalisasi berikut:

Pecahkan persamaannya .

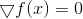
Tugasnya, secara sederhana, bukanlah tugas yang mudah. Jelas tidak lebih mudah dari aslinya. Namun, pada titik ini, kita dapat segera mencatat hubungan antara masalah minimisasi dan masalah penyelesaian sistem persamaan nonlinier. Koneksi ini akan kembali kepada kita ketika mempertimbangkan metode Levenberg-Marquardt (ketika kita sampai di sana). Sementara itu, ingat (atau cari tahu) bahwa salah satu metode yang paling umum digunakan untuk menyelesaikan sistem persamaan nonlinier adalah metode Newton. Terdiri dari fakta bahwa untuk menyelesaikan persamaan kita mulai dari beberapa perkiraan awal membangun urutan

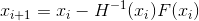
- Metode eksplisit Newton

atau

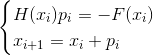
- Metode tersirat Newton

dimana - Matriks terdiri dari turunan parsial dari suatu fungsi . Secara alami, dalam kasus umum, ketika sistem persamaan nonlinier hanya diberikan kepada kita dalam sensasi, memerlukan sesuatu dari matriks kami tidak berhak. Dalam kasus ketika persamaan adalah kondisi minimum untuk beberapa fungsi, kita dapat menyatakan bahwa matriks simetris. Tapi tidak lebih.

Metode Newton untuk memecahkan sistem persamaan nonlinier telah dipelajari dengan cukup baik. Dan inilah masalahnya - untuk konvergensi, kepastian positif dari matriks tidak diperlukan . Ya, dan tidak bisa diminta - kalau tidak, dia tidak akan berharga. Sebaliknya, ada kondisi lain yang memastikan konvergensi lokal dari metode ini dan yang tidak akan kami pertimbangkan di sini, mengirim orang yang tertarik ke literatur khusus (atau dalam komentar). Kami mendapatkan bahwa pernyataan 2 salah.

Jadi?

Ya dan tidak Penyergapan di sini dalam kata ini adalah konvergensi lokal sebelum kata. Artinya perkiraan awal harus "cukup dekat" dengan solusi, jika tidak pada setiap langkah kita akan semakin jauh dari itu. Apa yang harus dilakukan Saya tidak akan masuk ke rincian tentang bagaimana masalah ini diselesaikan untuk sistem persamaan non-linear dari bentuk umum. Alih-alih, kembali ke tugas pengoptimalan kami. Kesalahan pertama dari pernyataan 2 sebenarnya adalah bahwa biasanya berbicara tentang metode Newton dalam masalah optimasi, itu berarti modifikasi - metode Newton teredam, di mana urutan perkiraan dibangun sesuai dengan aturan

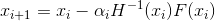
- Metode teredam eksplisit Newton

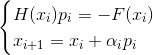
- Metode teredam implisit Newton

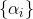
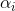
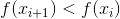
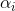
Ini urutannya adalah parameter dari metode dan konstruksinya adalah tugas yang terpisah. Dalam masalah minimisasi, wajar bila memilih akan ada persyaratan bahwa, pada setiap iterasi, nilai fungsi f menurun, yaitu . Muncul pertanyaan logis: apakah ada (positif) ? Dan jika jawaban untuk pertanyaan ini positif, maka disebut arah keturunan. Maka pertanyaannya dapat diajukan dengan cara ini:
Kapan arah yang dihasilkan oleh metode Newton adalah arah keturunan?
Dan untuk menjawabnya Anda harus melihat masalah minimisasi dari sisi lain.

Metode keturunan

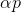
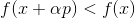
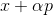
Untuk masalah minimisasi, pendekatan ini tampaknya cukup alami: mulai dari titik arbitrer, kami memilih arah p dalam beberapa cara dan mengambil langkah ke arah ini . Jika lalu ambil sebagai titik awal baru dan ulangi prosedur. Jika arah dipilih secara sewenang-wenang, maka metode seperti itu kadang-kadang disebut metode berjalan acak. Anda dapat menggunakan vektor satuan dasar sebagai arah - yaitu, ambil langkah hanya dalam satu koordinat, metode ini disebut metode penurunan koordinat. Tak perlu dikatakan, mereka tidak efektif? Agar pendekatan ini bekerja dengan baik, kami membutuhkan beberapa jaminan tambahan. Untuk melakukan ini, kami memperkenalkan fungsi bantu . 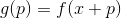Saya pikir itu jelas minimisasi sepenuhnya sama dengan meminimalkan . Jika dibedakan itu dapat direpresentasikan sebagai



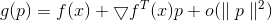
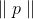
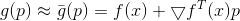
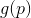
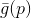
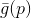
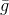
dan jika cukup kecil . Kami sekarang dapat mencoba mengganti masalah minimisasi tugas meminimalkan aproksimasi (atau model ) . Omong-omong, semua metode didasarkan pada penggunaan model disebut gradien. Tapi masalahnya adalah, Merupakan fungsi linier dan, karenanya, tidak memiliki minimum. Untuk mengatasi masalah ini, kami menambahkan batasan pada panjang langkah yang ingin kami ambil. Dalam hal ini, ini adalah persyaratan yang sepenuhnya alami - karena model kami kurang lebih menggambarkan fungsi objektif hanya di lingkungan yang cukup kecil. Akibatnya, kami memperoleh masalah tambahan tentang pengoptimalan bersyarat:



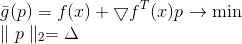
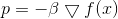
Tugas ini memiliki solusi yang jelas: dimana - Faktor yang menjamin pemenuhan kendala. Kemudian iterasi metode keturunan mengambil formulir

,

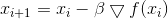
di mana kita belajar metode gradient descent yang terkenal. Parameter , yang biasanya disebut kecepatan turun, kini telah memperoleh makna yang dapat dipahami, dan nilainya ditentukan dari kondisi bahwa titik baru itu terletak pada bidang radius tertentu, dibatasi di sekitar titik lama.

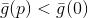
Berdasarkan pada sifat-sifat model yang dibangun dari fungsi tujuan, kita dapat berargumen bahwa ada , meskipun sangat kecil, bagaimana jika lalu . Perlu dicatat bahwa dalam hal ini arah di mana kita akan bergerak tidak tergantung pada ukuran jari-jari bola ini. Maka kita dapat memilih salah satu dari cara berikut:

1. Pilih menurut beberapa metode nilainya .
2. Tetapkan tugas memilih nilai yang sesuai memberikan penurunan nilai fungsi tujuan.

Pendekatan pertama adalah tipikal untuk metode wilayah kepercayaan , yang kedua mengarah pada perumusan masalah tambahan yang disebut pencarian linear (LineSearch) . Dalam kasus khusus ini, perbedaan antara pendekatan ini kecil dan kami tidak akan mempertimbangkannya. Sebaliknya, perhatikan hal-hal berikut:

mengapa, sebenarnya, kita mencari penyeimbang berbaring persis di bola?

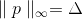
Faktanya, kita dapat mengganti batasan ini dengan persyaratan, misalnya, bahwa p termasuk permukaan kubus, mis., (dalam hal ini, itu tidak terlalu masuk akal, tetapi mengapa tidak), atau permukaan elips? Ini sudah tampak cukup logis, jika kita mengingat masalah yang muncul saat meminimalkan fungsi jurang. Inti dari masalah adalah bahwa di sepanjang garis koordinat fungsi berubah jauh lebih cepat daripada di sepanjang yang lain. Karena itu, kita dapatkan bahwa jika kenaikan itu harus menjadi milik bola, maka jumlahnya di mana "keturunan" disediakan harus sangat kecil. Dan ini mengarah pada fakta bahwa mencapai minimum akan membutuhkan sejumlah besar langkah. Tetapi jika sebaliknya kita mengambil elips yang cocok sebagai lingkungan, maka masalah ini secara ajaib akan sia-sia.

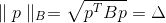
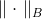
Dengan syarat bahwa titik-titik dari permukaan elips termasuk, dapat ditulis dimana Apakah beberapa matriks pasti positif, juga disebut metrik. Norma disebut norma elips yang disebabkan oleh matriks . Matriks macam apa ini dan dari mana mendapatkannya - kita akan mempertimbangkannya nanti, dan sekarang kita sampai pada tugas baru.



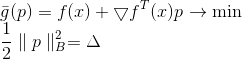
Kuadrat norma dan faktor 1/2 ada di sini semata-mata untuk kenyamanan, agar tidak mengacaukan akarnya. Menerapkan metode pengali Lagrange, kami mendapatkan masalah terikat dari optimasi tanpa syarat



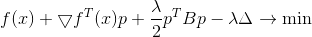
Syarat yang diperlukan untuk minimum untuk itu adalah

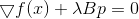
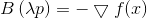
, atau dari mana







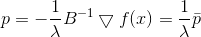
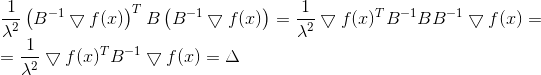
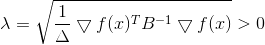
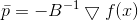
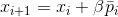
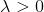
Sekali lagi kita melihat arahnya , di mana kami akan pindah, tidak tergantung pada nilai - hanya dari matriks . Dan lagi, kita bisa mengambilnya yang penuh dengan kebutuhan untuk menghitung dan inversi matriks eksplisit , atau memecahkan masalah pelengkap dalam menemukan bias yang cocok . Sejak , solusi untuk masalah tambahan ini dijamin ada.

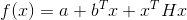
Jadi apa yang seharusnya untuk matriks B? Kami membatasi diri pada ide spekulatif. Jika fungsi objektif - kuadrat, yaitu memiliki bentuk dimana positif pasti, jelas bahwa kandidat terbaik untuk peran matriks adalah goni , karena dalam hal ini diperlukan satu iterasi dari metode keturunan yang telah kami bangun. Jika H tidak pasti positif, maka itu tidak bisa menjadi metrik, dan iterasi yang dibangun dengannya adalah iterasi dari metode Newton teredam, tetapi mereka bukan iterasi dari metode keturunan. Akhirnya, kita bisa memberikan jawaban yang tepat

Pertanyaan: Apakah matriks Hessian dalam metode Newton harus positif pasti?
Jawab: tidak, tidak diperlukan dalam metode standar atau metode Newton yang teredam. Tetapi jika kondisi ini dipenuhi, maka metode Newton yang teredam adalah metode turunan dan memiliki properti global , dan bukan hanya konvergensi lokal.

Sebagai ilustrasi, mari kita lihat bagaimana daerah kepercayaan terlihat ketika meminimalkan fungsi Rosenbrock yang terkenal menggunakan gradient descent dan metode Newton, dan bagaimana bentuk daerah mempengaruhi konvergensi proses.



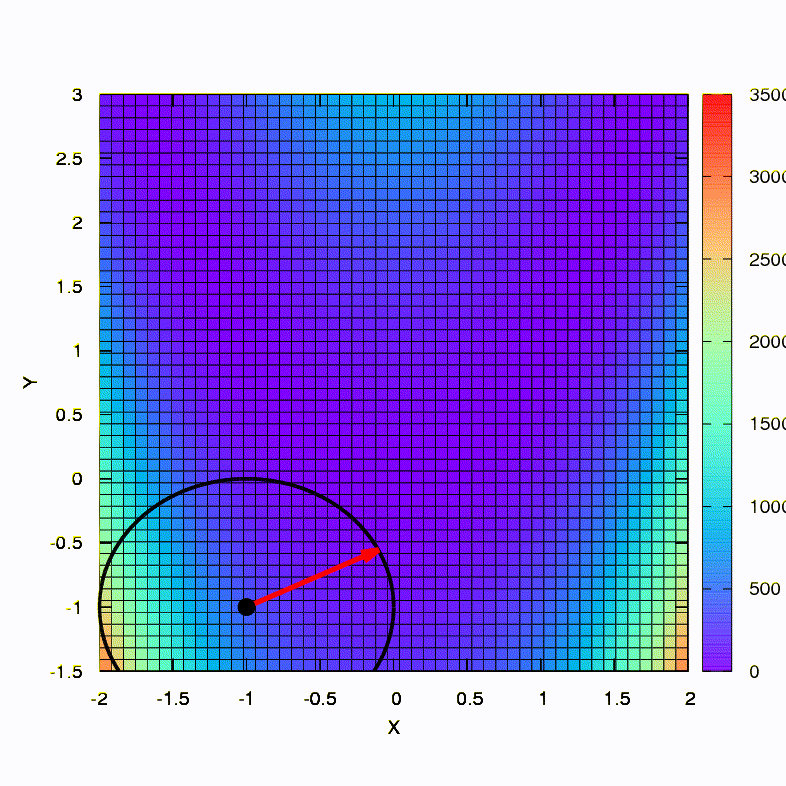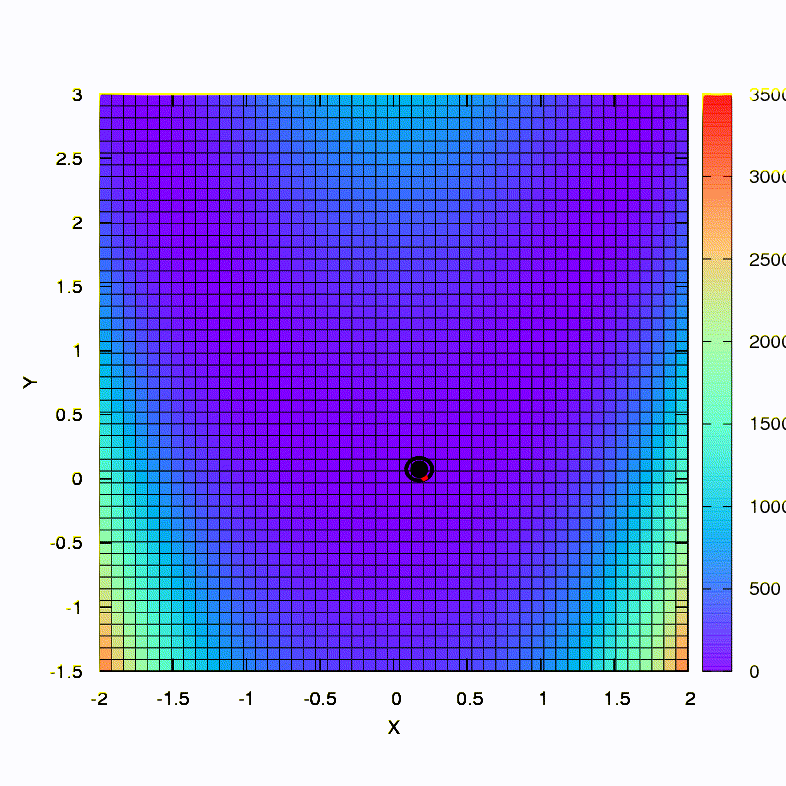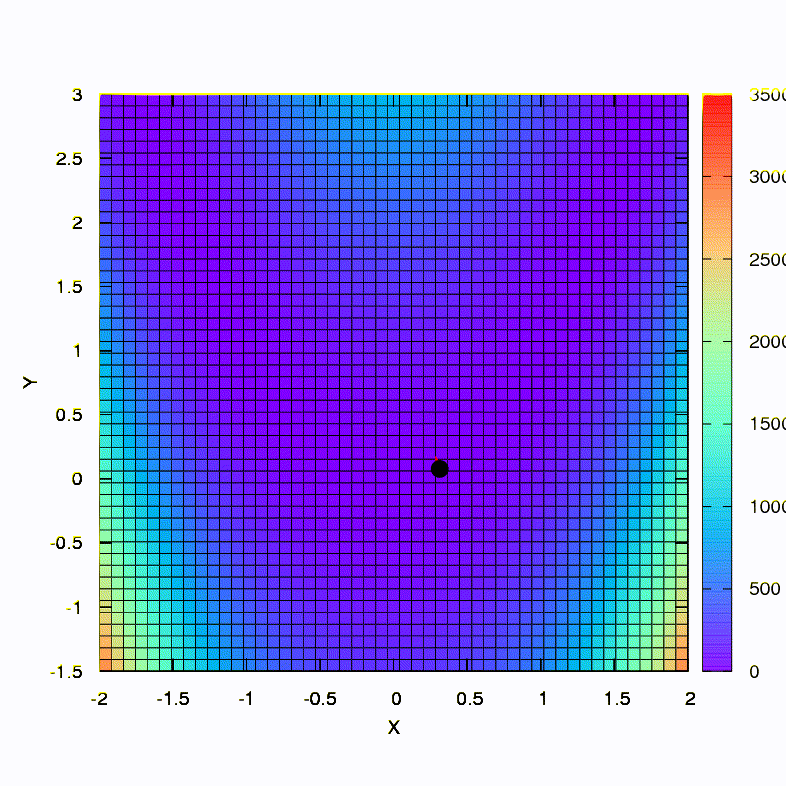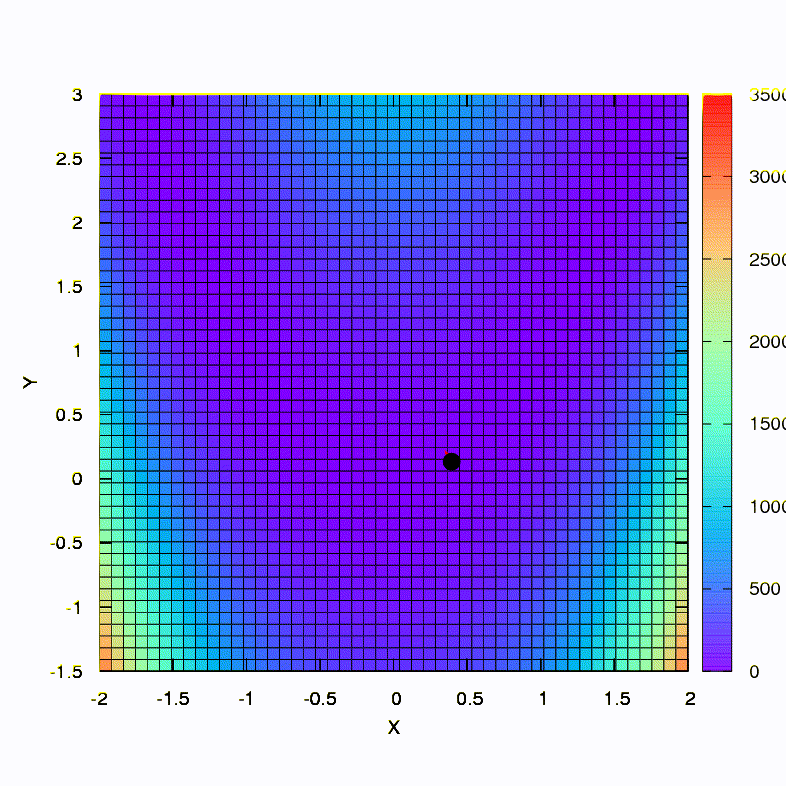
Ini adalah bagaimana metode keturunan berperilaku dengan wilayah kepercayaan bola, itu juga merupakan keturunan gradien. Semuanya seperti buku teks - kita terjebak di jurang.



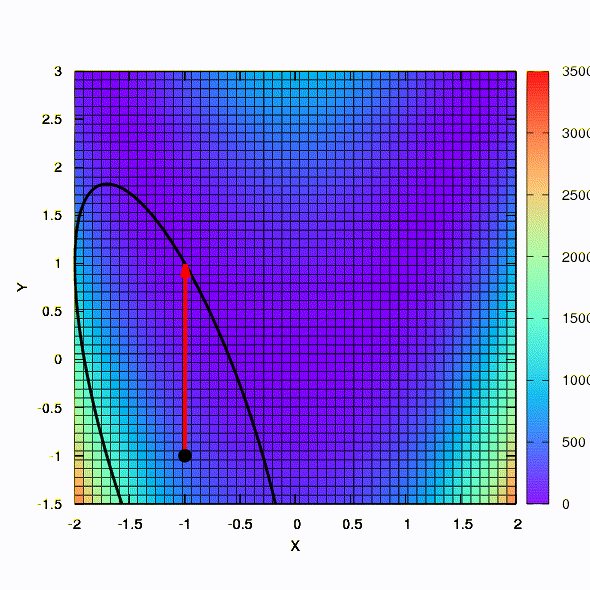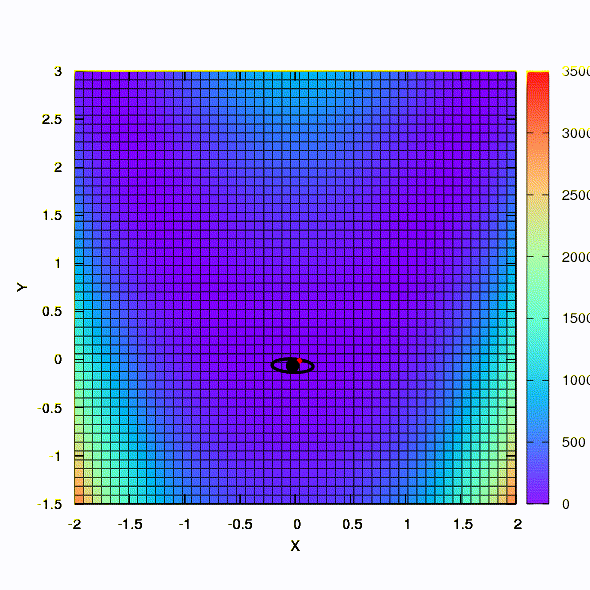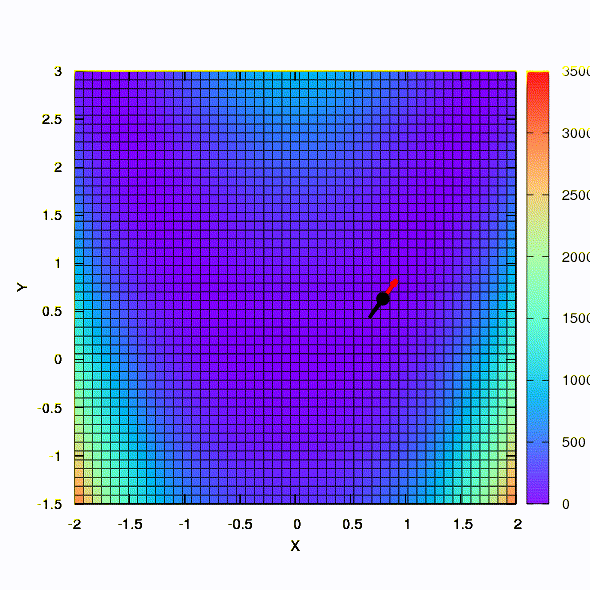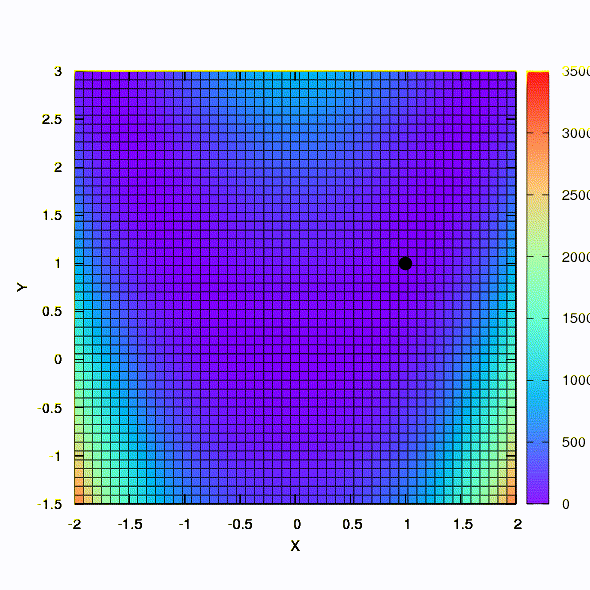
Dan ini kita dapatkan jika wilayah kepercayaan memiliki bentuk elips yang didefinisikan oleh matriks Hessian. Ini tidak lebih dari sebuah iterasi dari metode Newton yang teredam.

Hanya pertanyaan apa yang harus dilakukan jika matriks Hessian tidak pasti positif tetap belum terpecahkan. Ada banyak pilihan. Yang pertama adalah skor. Mungkin Anda beruntung dan iterasi Newton akan bertemu tanpa properti ini. Ini cukup nyata, terutama pada tahap akhir dari proses minimisasi, ketika Anda sudah cukup dekat dengan solusi. Dalam hal ini, iterasi metode Newton standar dapat digunakan tanpa repot mencari lingkungan yang diizinkan untuk turun. 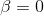Atau gunakan iterasi metode Newton teredam dalam kasus , yaitu, dalam kasus ketika arah yang diperoleh bukan arah keturunan, ubahlah, katakanlah, menjadi anti-gradien. Hanya saja, tidak perlu secara eksplisit memeriksa apakah Goni itu pasti positif menurut kriteria Sylvester , seperti yang dilakukan di sini !!! . Itu sia-sia dan sia-sia.
Metode yang lebih halus melibatkan membangun matriks, dalam arti dekat dengan matriks Hessian, tetapi memiliki sifat kepastian positif, khususnya, dengan mengoreksi nilai eigen. Topik terpisah adalah metode kuasi-Newtonian, atau metode metrik variabel, yang menjamin kepastian positif dari matriks B dan tidak memerlukan perhitungan turunan kedua. Secara umum, diskusi rinci tentang masalah-masalah ini melampaui ruang lingkup artikel ini.

Ya, dan omong-omong, ini mengikuti dari apa yang telah dikatakan bahwa metode teredam Newton dengan kepastian positif Hessian adalah metode gradien . Serta metode kuasi-Newtonian. Dan banyak lainnya, berdasarkan pilihan arah dan ukuran langkah yang terpisah. Jadi membandingkan metode Newton dengan terminologi gradien tidak benar.

Untuk meringkas

Metode Newton, yang sering diingat ketika membahas metode minimisasi, biasanya bukan metode Newton dalam pengertian klasiknya, tetapi metode keturunan dengan metrik yang ditentukan oleh Hessian tentang fungsi tujuan. Dan ya, itu konvergen secara global jika Goni di mana-mana pasti positif. Ini hanya mungkin untuk fungsi-fungsi cembung, yang jauh lebih jarang terjadi dalam praktik daripada yang kita inginkan, jadi dalam kasus umum, tanpa modifikasi yang sesuai, penerapan metode Newton (kami tidak akan melepaskan diri dari kolektif dan terus menyebutnya demikian) tidak menjamin hasil yang benar. Mempelajari jaringan saraf, bahkan yang dangkal, biasanya mengarah pada masalah optimisasi non-cembung dengan banyak minimum lokal. Dan inilah serangan baru. Metode Newton biasanya menyatu (jika menyatu) dengan cepat. Maksud saya sangat cepat. Dan anehnya, ini buruk, karena kita mencapai minimum lokal dalam beberapa iterasi. Dan untuk fungsi dengan medan yang kompleks bisa jauh lebih buruk daripada yang global. Keturunan gradien dengan pencarian linier konvergen jauh lebih lambat, tetapi lebih cenderung untuk "melewati" punggungan fungsi objektif, yang sangat penting dalam tahap awal minimisasi. Jika Anda telah mengurangi nilai fungsi objektif dengan baik, dan konvergensi penurunan gradien telah melambat secara signifikan, maka perubahan dalam metrik dapat mempercepat proses, tetapi ini adalah untuk tahap akhir.

Tentu saja, argumen ini tidak universal, tidak dapat disangkal, dan dalam beberapa kasus bahkan salah. Serta pernyataan bahwa metode gradien bekerja paling baik dalam masalah pembelajaran.