Algoritma Levenberg-Marquardt sederhana. Algoritma Levenberg-Marquardt efisien.
Dan mereka berkata tentang dia bahwa dia ada di suatu tempat di tengah-tengah antara gradien keturunan dan metode Newton, apa pun artinya. Ya, itu semacam
disortir dengan metode Newton dan hubungannya dengan gradient descent. Tetapi apa yang mereka maksudkan ketika mereka mengucapkan ungkapan yang mendalam ini? Mari kita coba sedikit menyelinap.
Dalam artikelnya, Kamerad Levenberg [K. Metode untuk Solusi Masalah-Masalah Tertentu di Kotak Terakhir. Quart. Appl. Matematika 1944. Vol. 2. P. 164-168.], Dan setelah dia warga Marquardt [Marquardt, Donald (1963). "Algoritma untuk Estimasi Terkecil-Kuadrat dari Parameter Nonlinier." Jurnal SIAM tentang Matematika Terapan. 11 (2): 431-441.] Dianggap sebagai masalah kuadrat terkecil, yang terlihat seperti ini:
,
yang dapat ditulis lebih mudah dalam bentuk vektor
.
Dan Anda bahkan dapat lebih mudah dengan sepenuhnya mencetak pada kuadrat terkecil. Ini tidak akan memengaruhi cerita.
Jadi, masalahnya dipertimbangkan
.
Masalah seperti itu muncul begitu sering sehingga pentingnya menemukan metode yang efektif untuk menyelesaikannya sulit ditaksir terlalu tinggi. Tapi kita akan mulai dari yang lain. Dalam artikel sebelumnya, ditunjukkan bahwa metode penurunan gradien yang terkenal, dan tidak hanya itu, dapat diperoleh dari pertimbangan berikut. Katakanlah kita sampai pada titik tertentu
di mana fungsi yang diminimalkan penting
. Kami mendefinisikan fungsi bantu pada titik ini
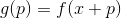
, serta beberapa modelnya
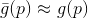
. Untuk model ini, kami menimbulkan masalah tambahan
dimana
- seperangkat nilai diizinkan yang telah ditentukan sebelumnya, dipilih sehingga masalahnya memiliki solusi dan fungsi sederhana
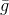
diperkirakan cukup akurat
pada
. Skema ini disebut metode wilayah kepercayaan, dan banyak
di mana nilai fungsi model diminimalkan - wilayah kepercayaan fungsi ini. Untuk gradient descent, kami ambil
, untuk metode Newton
, dan sebagai model untuk
bagian linear dari ekspansi Taylor
.
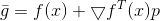
Mari kita lihat apa yang terjadi jika kita memperumit model dengan mengambil
.
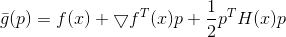
Kami meminimalkan fungsi model ini pada wilayah kepercayaan elips
(pengali ditambahkan untuk kemudahan perhitungan). Menerapkan metode pengali Lagrange, kami mendapatkan masalah
,
yang solusinya memuaskan kesetaraan
atau
Di sini, berbeda dengan apa yang kita lihat sebelumnya ketika menggunakan model linier, arah
p tidak hanya bergantung
pada metrik 
, tetapi juga pada pilihan
ukuran wilayah kepercayaan 
, yang berarti teknik pencarian linear tidak berlaku (setidaknya masuk akal). Ternyata sulit menentukan nilai secara eksplisit
sesuai dengan
. Namun, jelas bahwa dengan peningkatan
panjangnya
akan berkurang. Namun, jika kita masih memaksakan kondisinya
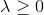
, maka panjang langkah tidak akan lebih dari apa yang akan diberikan metode Newton (serba modis, tanpa modifikasi dan ketentuan).
Jadi, kita bisa sebaliknya
mencari nilai yang tepat
, lakukan yang sebaliknya: temukan ini
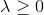
di bawah kondisi mana
. Ini adalah semacam pengganti untuk pencarian terlambat dalam hal ini. Marquardt mengusulkan prosedur sederhana berikut:
- jika untuk beberapa nilai kondisi
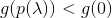dilakukan kemudian ulangi 
sampai 
- jika
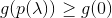lalu terima 
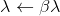dan ulangi.
Di sini
dan
Merupakan konstanta yang merupakan parameter metode. Perkalian dengan
sesuai dengan perluasan wilayah kepercayaan, dan multiplikasi oleh
- penyempitannya.
Teknik yang ditentukan dapat diterapkan pada fungsi objektif
apa pun . Perhatikan bahwa di sini ketetapan positif Hessian tidak lagi diperlukan, berbeda dengan kasus yang dipertimbangkan sebelumnya, ketika metode Newton disajikan sebagai kasus khusus dari metode keturunan sekuensial. Bahkan tidak diperlukan kemunduran, yang dalam beberapa kasus sangat penting. Namun, dalam hal ini, harga pencarian arah meningkat, karena setiap perubahan
mengarah pada kebutuhan untuk menyelesaikan sistem linear untuk menentukan
.
Mari kita lihat apa yang terjadi jika kita menerapkan pendekatan ini pada masalah kuadrat terkecil.
Fungsi Gradien
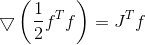
gubuknya
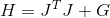
dimana
. Gantikan dan dapatkan sistem berikut yang menentukan arah pencarian
.
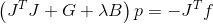
Ini cukup dapat diterima, tetapi menghitung turunan kedua dari fungsi vektor bisa sangat mahal. Marquardt mengusulkan untuk menggunakan fungsi itu sendiri untuk memotong masalah ini.
, dan pendekatan liniernya
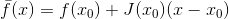
di mana matriks
berubah menjadi nol. Jika sekarang sebagai
ambil matriks identitas
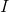
, lalu kita mendapatkan bentuk standar dari metode Levenberg-Marquardt untuk memecahkan masalah kuadrat terkecil:
.
Untuk metode penentuan arah keturunan ini, Marquardt membuktikan teorema itu dengan aspirasi
ke arah tanpa batas
cenderung anti-gradien. Pembaca yang tertarik dapat menemukan bukti yang kuat dalam artikel dasar, tetapi saya berharap bahwa pernyataan ini sendiri menjadi sangat jelas dari logika metode ini. Sampai batas tertentu, ini membenarkan referensi di mana-mana untuk fakta bahwa dengan peningkatan lambda (yang karena alasan tertentu saya sering menyebut parameter regularisasi) kita mendapatkan gradient descent. Sebenarnya, tidak ada yang semacam itu - kita akan mendapatkannya hanya dalam batas, di titik yang panjang langkahnya cenderung nol. Adalah jauh lebih penting bahwa dengan nilai lambda yang cukup besar, arah yang kita dapatkan adalah
arah keturunan , yang berarti kita mendapatkan
konvergensi global dari metode ini . Dan di sini adalah bagian kedua dari pernyataan bahwa ketika lambda cenderung nol kita mendapatkan metode Newton, itu jelas benar, tetapi hanya jika kita menerima sebaliknya
pendekatan liniernya
.
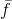
Tampaknya itu saja. Kami meminimalkan norma fungsi vektor dalam metrik elips - kami menggunakan Levenberg-Marquardt. Kami berhadapan dengan fungsi bentuk umum dan memiliki kemampuan untuk menghitung matriks turunan kedua - untuk Wells, gunakan metode wilayah kepercayaan wilayah umum. Tapi ada orang mesum ...
Terkadang metode Levenberg-Marquardt meminimalkan fungsi
mereka menyebut ungkapan seperti ini:
.
Segalanya tampak sama, tetapi di sini
- Matriks yang kedua! fungsi turunan
. Secara formal, ini memiliki hak untuk hidup, tetapi itu adalah penyimpangan. Dan inilah alasannya. Marquardt yang sama dalam artikelnya mengusulkan metode untuk menyelesaikan sistem persamaan
dengan meminimalkan fungsi
metode yang dijelaskan. Jika sebagai
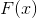
ambil gradien dari fungsi objektif, lalu kita benar-benar mendapatkan ekspresi yang dikurangi. Dan penyimpangan itu karena
masalah minimisasi yang dihasilkan oleh sistem persamaan nonlinier yang dihasilkan oleh masalah minimisasi diselesaikan .
Serangan ganda. Ungkapan seperti itu, setidaknya, tidak lebih baik daripada persamaan pertama dari wilayah kepercayaan bola, tetapi secara umum jauh lebih buruk baik dari sudut pandang produktivitas (operasi penggandaan yang tidak perlu, dan dalam implementasi normal - faktorisasi), dan dari sudut pandang stabilitas metode (penggandaan matriks dengan sendirinya memburuk pengkondisian). Terkadang keberatan itu
dijamin secara positif, tetapi dalam hal ini tidak masalah. Mari kita lihat metode Levenberg-Marquardt dari perspektif metode keturunan berurutan. Dalam kasus ini, ternyata kita ingin menggunakan matriks sebagai metrik
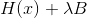
, dan agar dia bisa bertindak dalam kapasitas itu, artinya
harus memastikan kepastian positifnya. Mengingat itu
nilai pasti positif
selalu dapat ditemukan - dan karena itu tidak perlu menuntut dari
kepastian positif tidak diamati.
Sebagai sebuah matriks
tidak perlu mengambil unit, tetapi untuk model kuadrat fungsi objektif, menentukan wilayah kepercayaan yang memadai tidak lagi sesederhana untuk model linier. Jika kita mengambil daerah elips yang diinduksi oleh Hessian, maka metode tersebut berubah menjadi metode Newton (well, hampir)
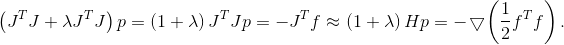
Kecuali, tentu saja, matriks Hessian pasti positif. Jika tidak, maka seperti sebelumnya, Anda dapat menggunakan Goni yang dikoreksi sebagai metrik, atau beberapa matriks yang dalam arti dekat dengannya. Ada juga rekomendasi untuk menggunakan matriks sebagai metrik
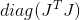
, yang oleh konstruksi dijamin pasti positif. Sayangnya, saya tidak tahu setidaknya ada pembenaran ketat untuk pilihan ini, tetapi hal ini sering disebut sebagai rekomendasi empiris.
Sebagai ilustrasi, mari kita lihat bagaimana metode berperilaku pada fungsi Rosenbrock yang sama, dan kita akan mempertimbangkannya dalam dua samaran - sebagai fungsi sederhana yang ditulis dalam bentuk
,
dan sebagai masalah kuadrat
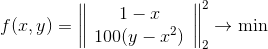
Ini adalah bagaimana suatu metode dengan wilayah kepercayaan bola bertindak.
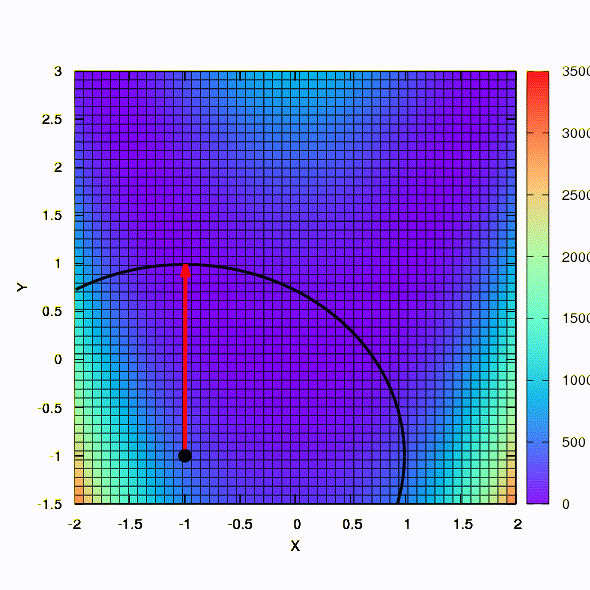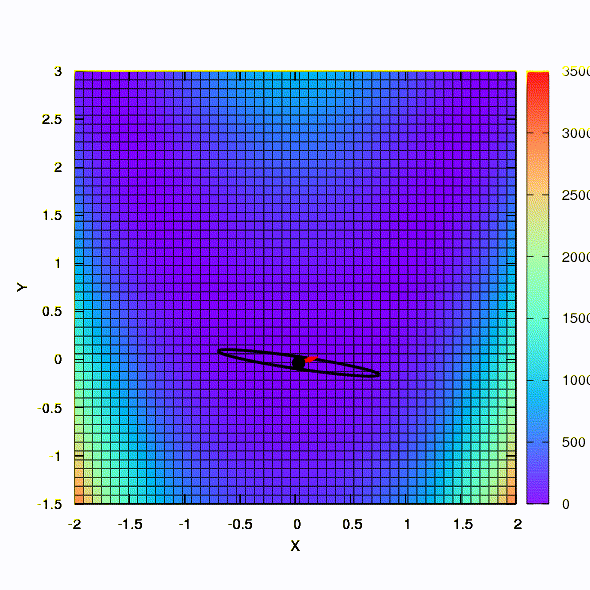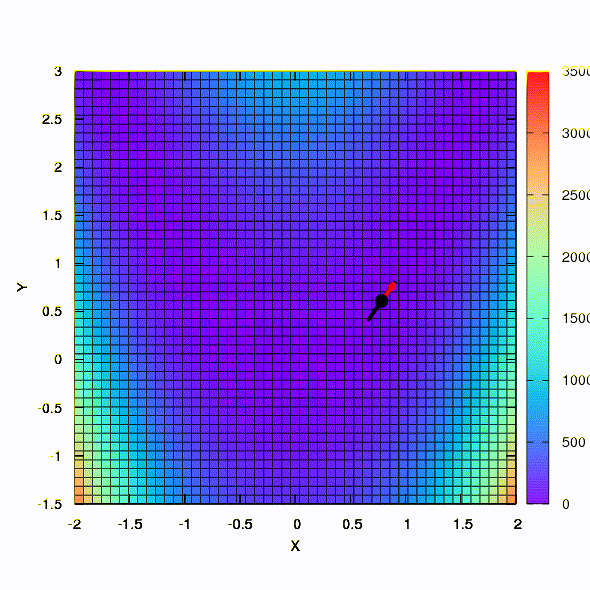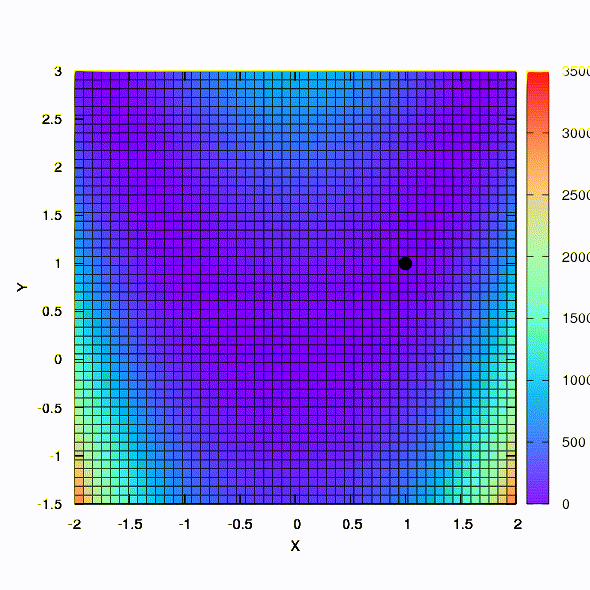
Jadi metode yang sama berlaku jika bentuk wilayah kepercayaan diberikan oleh matriks yang dibangun sesuai dengan aturan Davidon-Fletcher-Powell. Ada efek pada konvergensi, tetapi jauh lebih sederhana daripada dalam kasus serupa ketika menggunakan model linier dari fungsi tujuan.
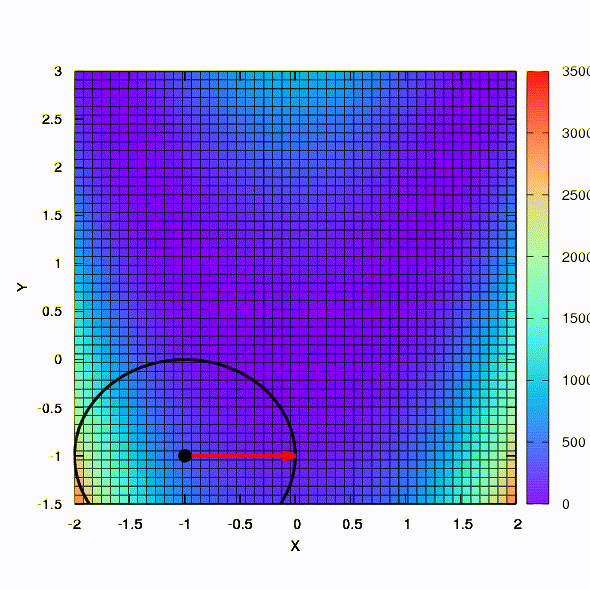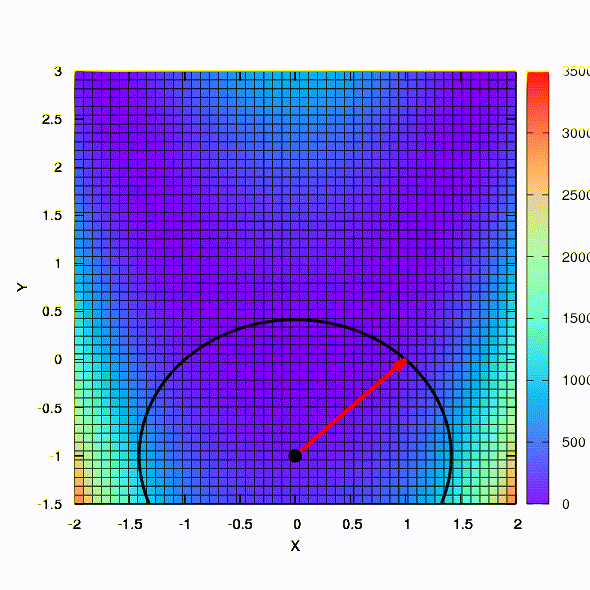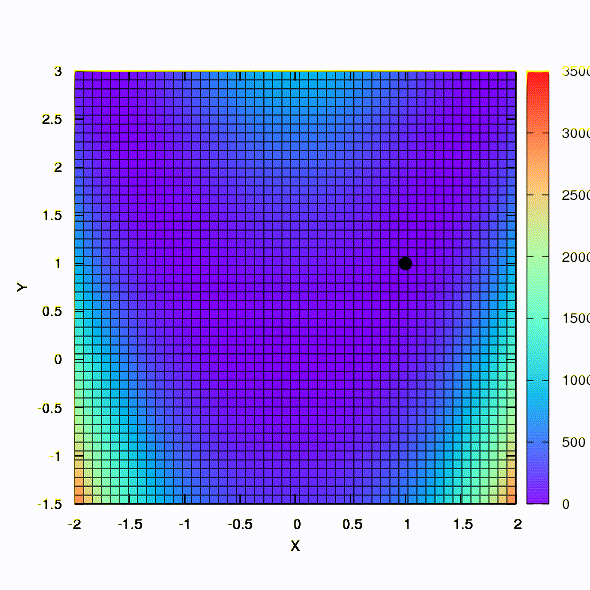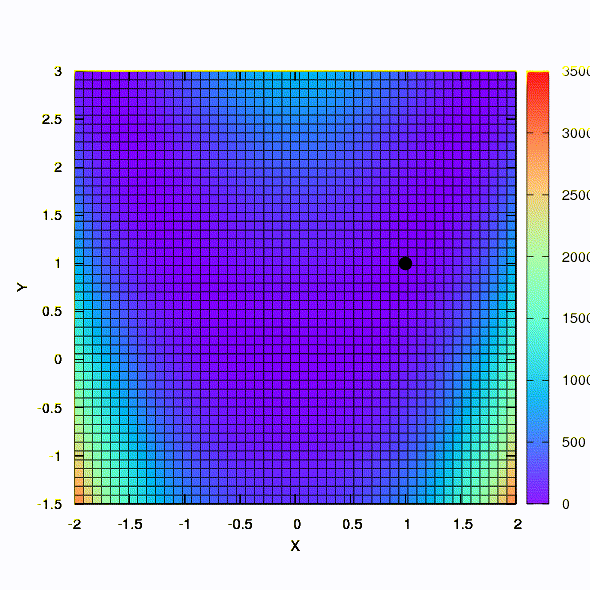
Dan ini adalah perilaku metode yang diterapkan pada masalah kuadrat terkecil. Ia menyatu dalam 5 iterasi. Tolong,
jangan menarik dari kesimpulan ini bahwa formulasi kedua untuk fungsi semacam ini selalu lebih baik daripada yang pertama . Ini tidak begitu, itu hanya terjadi dalam kasus khusus ini.
Kesimpulan
Metode Levenberg-Marquardt, sejauh yang saya tahu, adalah metode pertama yang didasarkan pada gagasan daerah yang bisa dipercaya. Dia menunjukkan dirinya dengan sangat baik dalam latihan ketika memecahkan masalah kuadrat-terkecil. Metode ini konvergen dalam banyak kasus (terlihat oleh saya) cukup cepat (saya katakan apakah itu baik atau buruk dalam artikel sebelumnya). Namun, sambil meminimalkan fungsi umum, itu bukan pilihan terbaik untuk memilih bola sebagai wilayah kepercayaan. Selain itu, kelemahan signifikan dari metode ini (dalam formulasi dasarnya, yang telah dijelaskan di sini) adalah bahwa ukuran wilayah kepercayaan ditetapkan secara implisit. Kerugiannya adalah mengetahui artinya
kami, tentu saja, dapat menghitung pada titik saat ini
hanya menghitung panjang langkahnya
. Namun, ketika kita pindah ke titik baru, nilainya sama
nilai yang sama sekali berbeda dari wilayah kepercayaan sudah sesuai. Dengan demikian, kita kehilangan kemampuan untuk menentukan ukuran "karakteristik untuk tugas" dari wilayah kepercayaan dan dipaksa untuk menentukan ukurannya dengan cara baru di setiap titik baru. Ini bisa menjadi signifikan ketika sejumlah iterasi yang cukup besar diperlukan untuk konvergensi, dan menghitung nilai fungsi mahal. Masalah serupa dipecahkan dengan metode yang lebih maju berdasarkan ide wilayah yang dapat dipercaya.
Tetapi ini adalah kisah yang sangat berbeda.
Selain itu
Berkat komentar berharga
Dark_Daiver, saya memutuskan bahwa di atas harus dilengkapi dengan komentar berikut. Tentu saja, seseorang dapat tiba di metode Levenberg-Marquardt dengan cara yang berbeda, murni empiris. Yaitu, mari kita kembali ke skema metode keturunan berurutan yang dijelaskan dalam artikel sebelumnya dan sekali lagi bertanya pada diri sendiri pertanyaan membangun metrik yang memadai untuk model linier fungsi objektif.
Misalkan matriks Hessian pada titik saat ini di ruang pencarian tidak pasti positif dan tidak dapat berfungsi sebagai metrik (apalagi, untuk memeriksa apakah ini benar, kami tidak memiliki kemampuan maupun keinginan). Ditunjukkan oleh
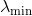
nilai eigen terkecilnya. Kemudian kita bisa mengoreksi Hessian hanya dengan menggeser semua nilai eigennya dengan
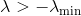
. Untuk melakukan ini, cukup tambahkan matriks ke Goni
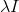
. Maka persamaan menentukan arah keturunan akan mengambil bentuk
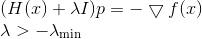
Jika kami memiliki skor lebih rendah untuk
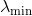
, maka kita bisa melakukan semua yang dilakukan dalam metode keturunan berurutan. Namun, jika kita tidak memiliki perkiraan seperti itu, maka pertimbangkan itu dengan peningkatan
panjang
p akan berkurang, kita dapat dengan yakin mengatakan bahwa ada yang cukup besar
itu pada saat yang sama
positif pasti dan
.
Kenapa saya menganggap kesimpulan metode seperti itu tidak terlalu berhasil. Pertama, sama sekali tidak jelas bahwa metrik yang dibangun dengan cara ini cocok untuk penggunaan praktis. Ini, tentu saja, menggunakan informasi tentang turunan kedua, tetapi tidak mengikuti dari mana saja yang menggeser nilai eigen dengan nilai yang diberikan tidak akan membuatnya tidak dapat digunakan. Seperti yang dicatat oleh kolega tersebut di komentar, tampak jelas bahwa menambahkan matriks identitas berskala ke matriks Hessian mengarah pada fakta bahwa wilayah kepercayaan elips akan cenderung bulat dan di sini lagi (seperti yang terlihat) masalah kemacetan di ngarai dan kelezatan lain dari penurunan gradien dan yang dekat harus merayap keluar baginya metode. Tetapi dalam praktiknya ini tidak terjadi. Bagaimanapun, saya tidak pernah bisa mengamati contoh yang menggambarkan perilaku seperti itu. Dalam hal ini, muncul pertanyaan:
tetapi, sebenarnya, mengapa ?
Tetapi pertanyaan seperti itu tidak muncul jika kita melihat metode ini bukan sebagai kasus khusus metode keturunan, tetapi sebagai metode wilayah kepercayaan dengan model kuadrat dari fungsi tujuan, karena jawabannya jelas: ketika lambda meningkat, kita hanya menekan bola - wilayah kepercayaan untuk model kita. Informasi tentang kelengkungan tidak pergi ke mana pun dan tidak tersapu oleh apa pun - kita hanya perlu memilih ukuran wilayah di mana model kuadratik secara memadai menggambarkan fungsi tujuan. Oleh karena itu, hampir tidak layak mengharapkan efek signifikan dari perubahan metrik, yaitu bentuk wilayah kepercayaan, karena semua informasi yang kita miliki tentang fungsi tujuan sudah diperhitungkan dalam modelnya.
Dan kedua, ketika mempertimbangkan suatu metode, penting untuk memahami ide utama yang mengarahkan Marquardt ke metode ini, yaitu, gagasan daerah yang dapat dipercaya. Memang, dalam analisis akhir, hanya memahami seluk beluk metode numerik yang akan memungkinkan kita untuk memahami mengapa ia bekerja dan, yang lebih penting, mengapa itu mungkin tidak berhasil.