Artikel ini akan membahas pengalaman mengembangkan program untuk membuat portofolio obligasi yang efektif dalam hal meminimalkan durasinya . Mungkin saya tidak akan menjadi orisinal dan bagi semua orang yang berinvestasi dalam obligasi, masalah penentuan bobot optimal telah lama diselesaikan, tetapi tetap saja, saya berharap bahwa pendekatan yang dijelaskan dan kode program yang disediakan akan bermanfaat bagi seseorang.

Artikel itu, karena kehadiran sejumlah kecil matematika di dalamnya, mungkin tampak rumit bagi seseorang. Tetapi jika Anda sudah memutuskan untuk mulai berinvestasi, maka Anda harus siap menghadapi kenyataan bahwa matematika sering ditemukan dalam kenyataan finansial dan bahkan lebih rumit.

Kode sumber program dan contoh portofolio untuk optimasi tersedia di GitHub.

UPDATE: Seperti yang dijanjikan, membuat layanan web sederhana yang membuat program tersedia untuk semua orang tanpa menyalin atau mengkompilasi kode.
tautannya
Instruksi untuk digunakan di tempat yang sama.
Jika sesuatu tidak berfungsi atau Anda perlu memperbaiki sesuatu - tulis di komentar.

Jadi, kami memiliki tugas membentuk portofolio obligasi yang efektif.

Bagian 1. Penentuan durasi portofolio

Dari sudut pandang meminimalkan risiko non-sistemik (untuk mana portofolio terdiversifikasi), pemilihan sekuritas dilakukan dengan mempertimbangkan parameter masalah tertentu, penerbit (jika tidak terbatas pada OFZ ), perilaku kertas, dll. (pendekatan untuk analisis semacam itu cukup individual untuk setiap investor dan tidak dipertimbangkan dalam artikel ini).

Setelah memilih beberapa sekuritas yang paling disukai untuk investasi, muncul pertanyaan alami: berapa banyak obligasi yang harus Anda beli? Ini adalah tugas mengoptimalkan portofolio sehingga risiko portofolio minimal.

Wajar untuk mempertimbangkan durasi sebagai parameter yang dioptimalkan. Dengan demikian, tugasnya adalah untuk menentukan bobot sekuritas dalam portofolio, sehingga durasi portofolio akan minimal untuk beberapa hasil portofolio tetap. Di sini Anda perlu melakukan beberapa pemesanan:

1. Durasi portofolio obligasi ditentukan oleh sekuritas penyusunnya. Durasi ini diketahui (mereka berada dalam domain publik). Durasi portofolio tidak sama dengan durasi maksimum dari sekuritas yang termasuk di dalamnya (ada kesalahan seperti itu). Hubungan antara jangka waktu sekuritas individu dan durasi seluruh portofolio tidak linier, yaitu. tidak sama dengan durasi rata-rata tertimbang dari obligasi konstituennya (Untuk memverifikasi ini, cukup untuk mempertimbangkan rumus durasi (lihat (1) di bawah) dan mencoba untuk menghitung durasi rata-rata tertimbang dari portofolio bersyarat yang terdiri, misalnya, dari dua makalah. Mengganti formula untuk durasi ke dalam ekspresi seperti itu) dari masing-masing kertas, pada output, kami tidak mendapatkan formula untuk durasi portofolio, tetapi semacam "omong kosong", dengan dua tingkat diskonto dan arus kas yang tidak konsisten sebagai bobot).
2. Tidak seperti durasi, pengembalian portofolio tergantung pada pengembalian instrumen yang dimasukkan di dalamnya secara linear. Yaitu dengan menempatkan uang di beberapa instrumen dengan pendapatan tetap, kita akan mendapatkan pengembalian yang berbanding lurus dengan volume investasi di setiap instrumen (dan ini bekerja untuk tingkat yang kompleks, dan bukan hanya untuk yang sederhana). Pastikan ini lebih mudah.
3. Yield to maturity ( YTM ) digunakan sebagai tingkat imbal hasil obligasi. Biasanya digunakan untuk menghitung durasi. Namun, hasil hingga jatuh tempo dari seluruh portofolio di sini agak sewenang-wenang jatuh tempo semua sekuritas berbeda. Ketika membentuk portofolio, fitur ini harus diperhitungkan dalam arti bahwa portofolio harus ditinjau, tidak kurang dari alat yang darinya disusun, keluar dari sirkulasi.

Jadi, tugas pertama adalah perhitungan yang benar dari durasi portofolio itu sendiri. Cara langsung untuk melakukan ini adalah: menentukan semua pembayaran untuk portofolio, menghitung hasil hingga jatuh tempo, pembayaran diskon, kalikan nilai yang diterima dengan ketentuan pembayaran ini dan tambahkan. Untuk melakukan ini, Anda perlu menggabungkan kalender pembayaran semua instrumen ke dalam satu kalender pembayaran untuk seluruh portofolio, menyusun ekspresi untuk menghitung hasil hingga jatuh tempo, menghitungnya, mendiskonnya untuk setiap pembayaran, dikalikan dengan tanggal jatuh tempo, tambahkan ... Secara umum, mimpi buruk. Untuk melakukan ini bahkan untuk dua makalah adalah tugas yang sangat melelahkan, belum lagi menghitung ulang portofolio di masa depan. Cara ini tidak cocok untuk kita.

Oleh karena itu, perlu mencari peluang untuk menentukan durasi portofolio dengan cara yang berbeda dan lebih cepat. Opsi yang dapat diterima adalah opsi yang memungkinkan Anda menentukan durasi portofolio berdasarkan durasi instrumen yang diketahui. Studi tentang rumus durasi telah menunjukkan bahwa ada jalan seperti itu dan di sini saya ingin memberikannya secara rinci (jika seseorang tidak tertarik dengan rincian perhitungan matematis, Anda dapat dengan aman melewati beberapa paragraf dengan rumus dan langsung ke contoh).

Durasi instrumen hutang didefinisikan sebagai berikut:

$$$$ menampilkan $$ \ mulai {persamaan} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~ (1) \ end {persamaan} $$ menampilkan $$

dimana:

• t _i adalah saat waktu pembayaran ke-i;
• $$$ sebaris $ \ mulai {persamaan} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {persamaan} $ sebaris $ - pembayaran diskon ke-i;
• CF _i - pembayaran ke-i;
• r adalah tingkat diskonto.

Kami memperkenalkan koefisien diskon k = (1 + r) dan mempertimbangkan jumlah pembayaran diskon P sebagai fungsi dari k :

$$$$ menampilkan $$ \ mulai {persamaan} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~ ~~~~ (2) \ end {persamaan} $$ menampilkan $$

Membedakan P sehubungan dengan k, kita dapatkan

$$$$ menampilkan $$ \ begin {persamaan} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {persamaan} $$ tampilkan $$

Mengingat yang terakhir, ungkapan untuk durasi ikatan mengambil bentuk

$$$$ menampilkan $$ \ mulai {persamaan} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~ (4) \ end {persamaan} $$ tampilan $$

Pada saat yang sama, kita ingat bahwa sebagai tingkat diskonto r dalam kasus obligasi, yield to maturity (YTM) digunakan.

Ekspresi yang diperoleh valid untuk satu obligasi, tetapi kami tertarik pada portofolio obligasi. Mari kita beralih ke menentukan durasi portofolio.

Kami memperkenalkan notasi berikut:

• P _i adalah harga obligasi ke-i;
• z _i - jumlah sekuritas obligasi ke-i dalam portofolio;
• k _i - koefisien diskon ikatan ke-i dalam portofolio;
• $$$ sebaris $ \ mulai {persamaan} P_p = \ sum_ {i} {z_iP_i} \ end {persamaan} $ sebaris $ - harga portofolio;
• $$$ sebaris $ \ mulai {persamaan} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {persamaan} $ inline $ $ - bobot ikatan ke-i dalam portofolio; persyaratan yang jelas$$ $ sebaris $ \ mulai {persamaan} \ sum_ {i} w_i = 1 \ end {persamaan} $ sebaris $ ;
• $$$ sebaris $ \ mulai {persamaan} k_p = \ sum_ {i} w_ik_i \ end {persamaan} $ sebaris $ - koefisien diskon portofolio;

Karena linearitas diferensiasi, berikut ini benar:

$$$$ menampilkan $$ \ mulai {persamaan} P'_p (k) = \ kiri (\ sum_ {i} z_iP_i (k) \ kanan) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~ (5) \ end {persamaan} $$ menampilkan $$

Dengan demikian, dengan mempertimbangkan (4) dan (5), durasi portofolio dapat dinyatakan sebagai

$$$$ menampilkan $$ \ mulai {persamaan} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ kiri (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ kanan) ~~~~~~~~~~~~~~ (6) \ end {persamaan} $$ menampilkan $$

Dari (4) ia mengikuti dengan jelas$$ $ sebaris $ \ mulai {persamaan} P'_j = - \ frac {D_jP_j} {k_j} \ end {persamaan} $ sebaris $ .
Mengganti ungkapan ini dalam (6), kita sampai pada formula berikut untuk durasi portofolio:

$$$$ menampilkan $$ \ mulai {persamaan} D_p = \ sum_ {i} w_ik_i \ kiri (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ kanan) = \ kiri (\ sum_ {i} w_ik_i \ kanan) \ kiri (\ sum_ {j} w_j \ frac {D_j} {k_j} \ kanan) ~~~~~~~~~~~~~ (7) \ end {persamaan} $$ menampilkan $$

Dalam kondisi ketika durasi dan hasil hingga jatuh tempo dari masing-masing instrumen diketahui (dan kita ingat, kita hanya dalam kondisi seperti itu), ekspresi (7) adalah formula yang diinginkan untuk menentukan durasi portofolio berdasarkan durasi obligasi. Tampaknya hanya rumit dalam penampilan, tetapi sebenarnya sudah siap untuk penggunaan praktis dengan bantuan fungsi paling sederhana dari MS Excel, yang sekarang akan kita lakukan dengan sebuah contoh.

Contoh

Untuk menghitung durasi portofolio menurut rumus (7), kita membutuhkan input data yang mencakup sekuritas sekuritas sebenarnya yang termasuk dalam portofolio, durasinya, dan hasil hingga jatuh tempo. Seperti disebutkan di atas, informasi ini tersedia untuk umum, misalnya, di situs web rusbonds.ru di bagian analisis obligasi. Sumber data dapat diunduh dalam format Excel.

Sebagai contoh, pertimbangkan portofolio efek yang terdiri dari 9 obligasi. Tabel data asli yang diunduh dari rusbonds memiliki formulir berikut.



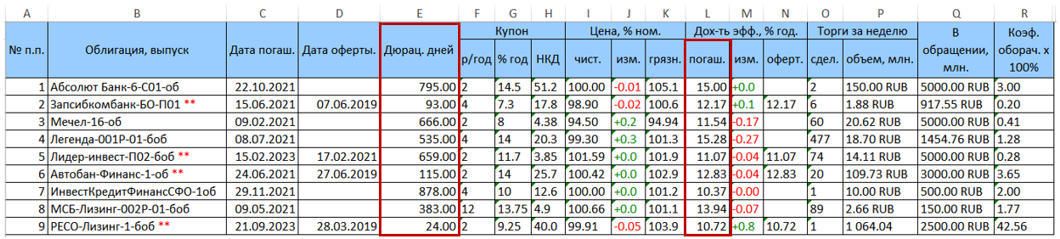
Dua kolom yang menarik bagi kami dengan durasi (kolom E) dan hasil hingga jatuh tempo (kolom L = YTM) disorot dalam warna merah.

Kami menetapkan bobot untuk obligasi dalam portofolio ini (sejauh ini dengan cara sewenang-wenang, tetapi agar jumlahnya sama dengan kesatuan) dan menghitung k = (1 + YTM / 100) dan D / k = ("kolom E" / k). Tabel yang dikonversi (tanpa kolom tambahan) akan terlihat seperti



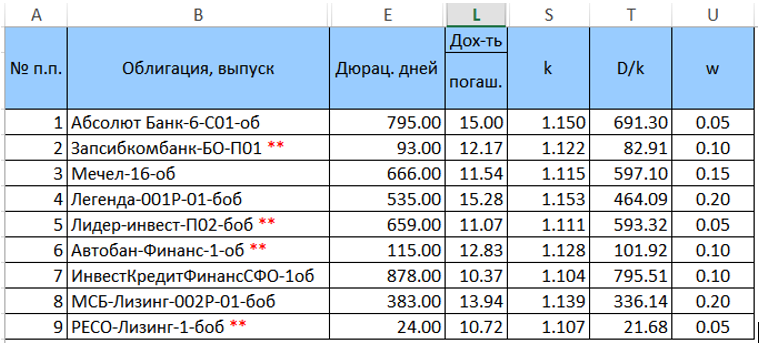
Selanjutnya, kami menghitung produk$$ $ sebaris $ \ mulai {persamaan} w_j \ frac {D_j} {k_j} \ end {persamaan} $ sebaris $ dan$$ $ sebaris $ \ mulai {persamaan} w_ik_i \ end {persamaan} $ sebaris $ dan menjumlahkannya, dan mengalikan jumlah yang dihasilkan oleh satu dengan yang lain. Hasil dari perkalian ini akan menjadi durasi yang diinginkan untuk distribusi bobot yang diberikan.



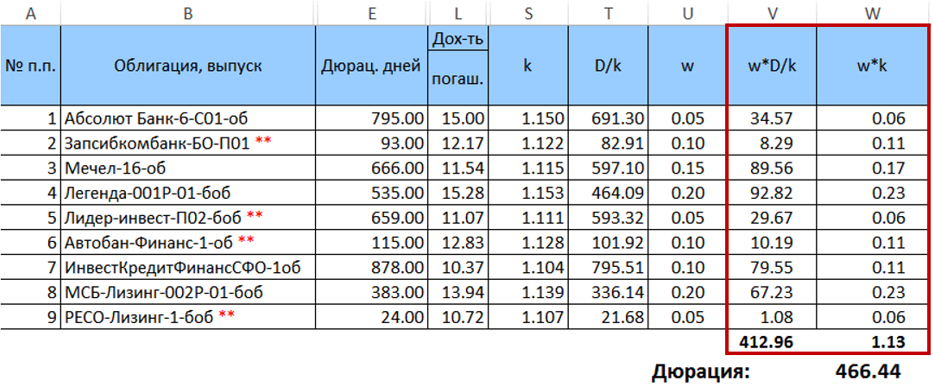
Jadi, durasi portofolio yang diinginkan adalah 466,44 hari. Penting untuk dicatat bahwa dalam kasus khusus ini, durasi yang dihitung dengan rumus (7) sangat sedikit berbeda dari durasi rata-rata tertimbang yang dihitung dengan bobot yang sama (penyimpangan <0,5 hari). Namun, perbedaan ini meningkat dengan meningkatnya dispersi bobot. Ini juga akan meningkat dengan meningkatnya penyebaran durasi kertas.

Setelah kami mendapatkan formula untuk menghitung durasi portofolio, langkah selanjutnya adalah menentukan bobot sekuritas sehingga pada hasil yang diberikan durasi estimasi portofolio akan minimal. Kami beralih ke bagian selanjutnya - optimalisasi portofolio.

Bagian 2. Optimalisasi Portofolio Obligasi

Ekspresi (7) adalah bentuk kuadratik, dengan matriks

$$$$ menampilkan $$ \ begin {persamaan} A = \ kiri \ {k_i \ frac {D_j} {k_j} \ kanan \} = \ begin {pmatrix} D_1 & \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {persamaan} $$ tampilkan $$

Dengan demikian, dalam bentuk matriks, ungkapan untuk durasi portofolio (7) dapat ditulis sebagai berikut:

$$$$ menampilkan $$ \ mulai {persamaan} D_p = w ^ TAw ~~~~~~~~~~~~~ (8) \ end {persamaan} $$ tampilkan $$

di mana w adalah vektor kolom bobot obligasi dalam portofolio. Seperti disebutkan di atas, jumlah elemen vektor w harus sama dengan kesatuan. Di sisi lain, ekspresi $$$k_p = \ sum_ {i} w_i k_i$ (yang, pada dasarnya, adalah produk skalar sederhana ( w , k ) , di mana k adalah vektor koefisien diskon obligasi) harus sama dengan tingkat diskonto target portofolio, dan karenanya pengembalian portofolio target harus ditetapkan.

Dengan demikian, tugas mengoptimalkan portofolio obligasi adalah untuk meminimalkan fungsi kuadrat (8) dengan kendala linier.

Metode klasik untuk menemukan ekstrem bersyarat dari fungsi beberapa variabel adalah metode pengali Lagrange. Namun, metode ini tidak berlaku di sini, jika hanya karena matriks A mengalami degenerasi oleh konstruksi (tetapi bukan hanya karena ini; kami menghilangkan rincian analisis penerapan metode Lagrange di sini agar tidak membebani artikel dengan konten matematika yang berlebihan).

Ketidakmampuan untuk menerapkan metode analitik yang mudah dan terjangkau menyebabkan kebutuhan untuk menggunakan metode numerik. Masalah optimalisasi fungsi kuadratik sudah dikenal dan memiliki beberapa algoritma efisien yang telah lama diimplementasikan di perpustakaan umum.

Untuk mengatasi masalah khusus ini, perpustakaan ALGLIB dan algoritma optimisasi kuadratik yang diterapkan di dalamnya, QP-Solvers , termasuk dalam paket minqp, digunakan.

Masalah optimasi kuadrat secara umum adalah sebagai berikut:

Diperlukan untuk menemukan vektor n-dimensi dengan meminimalkan fungsi

$$$$ menampilkan $$ \ mulai {persamaan} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~ (9) \ end {persamaan} $$ tampilan $$

Dengan batasan yang diberikan
1) l ≤ w ≤ u ;
2) Cw * d ;
di mana w, l, u, d, b adalah vektor bernilai riil n-dimensi, Q adalah matriks simetris dari bagian kuadratik, dan tanda * berarti salah satu dari hubungan ≥ = ≤.
Seperti dapat dilihat dari (8), bagian linier bTw dalam fungsi objektif kami sama dengan nol. Namun, matriks A tidak simetris, yang, bagaimanapun, tidak mencegah membawanya ke bentuk simetris tanpa mengubah fungsi itu sendiri. Untuk melakukan ini, cukup cantumkan A ekspresi$$ $ sebaris $ \ mulai {persamaan} \ frac {A ^ T + A} {2} \ end {persamaan} $ sebaris $ Karena rumus (9) termasuk koefisien $$$\ frac {1} {2}$ maka kita sebagai Q kita dapat menerima $$$A ^ T + A$ .

Koordinat vektor l dan u menentukan batas-batas vektor yang diinginkan dan terletak pada kisaran [-1,1]. Karena kita tidak mengasumsikan penjualan obligasi pendek, koordinat vektor dalam kasus kami semuanya tidak kurang dari 0. Dalam contoh program di bawah ini, untuk kesederhanaan, vektor l diasumsikan nol, dan koefisien vektor u semuanya 0,3 . Namun, tidak ada yang mencegah kami meningkatkan program dan membuat vektor kendala lebih dapat disesuaikan.

Matriks C dalam kasus kami akan terdiri dari dua baris: 1) koefisien diskon, yang, ketika dikalikan secara skal dengan bobot (sama ( w , k )), harus memberikan tingkat pengembalian target pada portofolio; 2) string yang terdiri dari unit. Diperlukan untuk menetapkan batas $$$\ sum_ {i} w_i = 1$ .

Dengan demikian, ekspresi Cw * d untuk tugas kita akan terlihat seperti ini:

$$$$ menampilkan $$ \ begin {persamaan} \ kiri \ {\ begin {array} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ benar ~~~~~~~~~~~~~ (10) \ end {persamaan} $$ menampilkan $$

Kami sekarang beralih ke implementasi perangkat lunak dari pencarian portofolio optimal. Dasar pengoptimal kuadrat di ALGLIB adalah objek $$$\ tt \ minqpstate kecil$

alglib::minqpstate state; 

Untuk menginisialisasi pengoptimal, objek ini diteruskan ke fungsi minqpcreate bersama dengan parameter dimensi tugas n

 alglib::minqpcreate(n, state); 

Poin terpenting berikutnya adalah pilihan algoritma optimisasi (pemecah). Pustaka ALGLIB untuk optimasi kuadrat menawarkan tiga solusi:

• QP-BLEIC adalah algoritma paling universal yang dirancang untuk menyelesaikan masalah dengan jumlah yang tidak terlalu besar (hingga 50 sesuai dengan rekomendasi dokumentasi) jumlah kendala linear (dari bentuk Cw * d ). Pada saat yang sama, ini bisa efektif pada tugas-tugas berdimensi besar (seperti klaim dokumentasi - hingga n = 10000).
• QuickQP adalah algoritma yang sangat efisien, terutama ketika fungsi cembung dioptimalkan. Namun, sayangnya, itu tidak dapat bekerja dengan batasan linear - hanya dengan kondisi batas (dari bentuk l≤w≤u ).
• Dense-AUL - dioptimalkan untuk kasus dimensi yang sangat besar dan sejumlah besar pembatasan. Tetapi, menurut dokumentasi, tugas berdimensi kecil dan jumlah pembatasan akan lebih efisien diselesaikan dengan menggunakan algoritma lain.

Mengingat karakteristik di atas, jelas bahwa pemecah QP-BLEIC paling cocok untuk tugas kita.

Untuk menginstruksikan pengoptimal menggunakan algoritma ini, Anda harus memanggil fungsi $$$\ tt \ small minqpsetalgobleic$ . Objek itu sendiri dan kriteria berhenti diteruskan ke fungsi ini, di mana kita tidak akan tinggal lebih detail: dalam program yang dipertimbangkan di sini, nilai default digunakan. Panggilan fungsi adalah sebagai berikut:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

Inisialisasi lebih lanjut dari pemecah meliputi:

• Transfer matriks bagian kuadratik Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (status, qpma);$
• Transmisi vektor dari bagian linear (dalam kasus kami, vektor nol) - $$$\ tt \ small alglib :: minqpsetlinearterm (state, b);$
• Pemindahan vektor kondisi batas l dan u - $$$\ tt \ small alglib :: minqpsetbc (status, bndl, bndu);$
• Transmisi Linier - $$$\ tt \ small alglib :: minqpsetlc (status, c, ct);$
• Mengatur skala koordinat ruang vektor $$$\ tt \ small alglib :: minqpsetscale (status, s);$

Mari kita bahas setiap item:
Untuk menentukan vektor dan matriks, pustaka ALGLIB menggunakan objek tipe khusus (integer dan bernilai riil): $$$\ tt \ small alglib :: integer \ _1d \ _array$ , $$$\ tt \ small alglib :: real \ _1d \ _array$ , $$$\ tt \ small alglib :: integer \ _2d \ _array$ , $$$\ tt \ small alglib :: real \ _2d \ _array$ . Untuk menyiapkan matriks, kita perlu sebuah tipe $$$\ tt \ small real \ _2d \ _array$ . Dalam program ini, pertama buat matriks A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$ ), dan kemudian sesuai dengan rumus $$$Q = A ^ T + A$ dari sini kita membangun matriks Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$ ) Mengatur dimensi matriks dalam ALGLIB adalah fungsi terpisah $$$\ tt \ setlength kecil (n, m)$ .

Untuk membangun matriks, kita perlu vektor koefisien diskon ( k _i ) dan hubungan durasi dengan koefisien ini ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

Cuplikan kode yang mengimplementasikan konstruksi matriks ditunjukkan dalam daftar berikut:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

Vektor dari bagian linear, seperti yang telah ditunjukkan, adalah nol dalam kasus kami, jadi semuanya sederhana dengan itu:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

Kondisi batas vektor ditransmisikan oleh satu fungsi. Untuk mengatasi masalah ini, diterapkan syarat batas yang sangat sederhana: berat masing-masing kertas tidak boleh kurang dari nol (kami tidak mengizinkan posisi negatif) dan tidak boleh melebihi 30%. Jika diinginkan, batasannya bisa rumit. Eksperimen dengan program menunjukkan bahwa bahkan perubahan sederhana dalam kisaran ini dapat sangat memengaruhi hasil. Dengan demikian, peningkatan batas bawah dan / atau penurunan batas atas mengarah ke diversifikasi yang lebih besar dari portofolio akhir, karena selama optimasi pemecah dapat mengecualikan beberapa sekuritas dari vektor yang dihasilkan (menetapkan mereka bobot 0%) sebagai tidak cocok. Jika Anda menetapkan batas bawah skala, katakanlah, pada 5%, maka semua kertas dijamin akan dimasukkan dalam portofolio. Namun, durasi yang dihitung pada pengaturan tersebut tentu saja akan lebih besar daripada dalam kasus ketika optimizer dapat mengecualikan kertas.

Jadi, syarat batas diatur oleh dua vektor dan ditransfer ke pemecah:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

Selanjutnya, pengoptimal perlu melewati batasan linear yang ditentukan oleh sistem (10). Dalam ALGLIB, ini dilakukan menggunakan fungsi $$$\ tt \ small alglib :: minqpsetlc (status, c, ct)$ , di mana c adalah matriks yang menggabungkan sisi kiri dan kanan sistem (10), yaitu lihat matriks $$$(C ~~ d)$ , dan ct adalah vektor hubungan (mis., korespondensi dari bentuk ≥, =, atau ≤). Dalam kasus kami, ct = (0,0), yang sesuai dengan rasio '=' untuk kedua baris sistem (10).

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

Dokumentasi untuk perpustakaan ALGLIB sangat merekomendasikan pengaturan skala variabel sebelum memulai pengoptimal. Ini sangat penting jika variabel diukur dalam satuan, perubahannya berbeda berdasarkan urutan besarnya (misalnya, ketika mencari solusi, ton dapat diubah dalam ratusan atau ribuan, dan meter dalam satuan; masalahnya dapat diselesaikan dalam ruang ton-meter), yang mempengaruhi kriteria untuk pengabaian. Namun, ada reservasi yang dengan skala variabel yang sama, pengaturan skala tidak diperlukan. Dalam program yang sedang dipertimbangkan, kami masih melakukan tugas skala demi lebih kerasnya pendekatan, terutama karena sangat mudah dilakukan.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

Selanjutnya, kami menetapkan pengoptimal sebagai titik awal. Secara umum, langkah ini juga opsional, dan program berhasil mengatasi tugas tanpa titik awal yang jelas. Demikian pula, untuk alasan ketelitian, kami menetapkan titik awal. Kami tidak akan pintar: titik awal akan menjadi titik dengan bobot yang sama untuk semua obligasi.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

Tetap menentukan variabel ke mana pengoptimal akan mengembalikan solusi yang ditemukan dan variabel status. Kemudian Anda dapat menjalankan pengoptimalan dan memproses hasilnya

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

Khususnya, runtime program tidak diukur dalam percobaan, tetapi semuanya bekerja sangat cepat. Pada saat yang sama, jelas bahwa seorang investor swasta tidak mungkin untuk mengoptimalkan portofolio lebih dari 10-15 obligasi.

Penting juga untuk mencatat hal-hal berikut. Pengoptimal mengembalikan tepat vektor bobot. Untuk mendapatkan durasi yang dihitung sendiri, Anda harus langsung menggunakan rumus (8). Program dapat melakukan ini. Untuk tujuan ini, dua fungsi mengalikan vektor dan matriks ditambahkan secara khusus. Kami tidak akan memberikannya di sini. Mereka yang berharap sendiri akan dengan mudah menemukannya dalam kode sumber yang dipublikasikan.

Itu saja. Investasi efektif dalam instrumen utang untuk semua orang.

PS Memahami bahwa memilih kode orang lain bukanlah pekerjaan yang paling menarik, dan bagi banyak orang yang ingin berinvestasi, itu sama sekali tidak terspesialisasi, saya akan mencoba menggeser program ini sedikit kemudian menjadi layanan web sederhana yang dapat digunakan semua orang, terlepas dari pengetahuan matematika. dan pemrograman.