Euler-Poisson terpisahkan. Detail tentang metode perhitungan

Dalam artikel tersebut, secara rinci, hingga ke detail terkecil, tiga metode untuk mengambil integral Euler-Poisson dipertimbangkan. Dalam salah satu metode, formula reduksi bantu diturunkan. Untuk menemukan beberapa integral yang kompleks, seseorang dapat menggunakan rumus reduksi yang memungkinkan seseorang untuk menurunkan derajat integrand dan menghitung integral terkait dalam sejumlah langkah terbatas.

Integral ini diambil dari fungsi Gaussian: $$$I = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx}$
Ada cara matematis yang sangat menarik. Untuk menemukan integral asli, pertama mencari kuadrat integral ini, dan kemudian mengambil root dari hasilnya. Mengapa Ya, karena jauh lebih mudah dan tidak menyakitkan untuk pergi ke koordinat kutub. Oleh karena itu, pertimbangkan kuadrat integral Gaussian:
$$$I ^ 2 = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} \ int \ limit_0 ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limit_0 ^ \ infty { \ int \ limit_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ kanan)}}} dxdy$
Kita melihat bahwa kita mendapatkan integral ganda dari suatu fungsi $$$g \ kiri ({x, y} \ kanan) = \ exp \ kiri [{- \ kiri ({x ^ 2 + y ^ 2} \ kanan)} \ kanan]$ . Pada akhir permukaan ini integral adalah elemen area dalam sistem koordinat Cartesian $$$dS = dxdy$ .
Sekarang mari kita pindah ke sistem koordinat kutub:

$$

$$\ begin {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ kiri. \ begin {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ kanan | \ to x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ hingga x ^ 2 + y ^ 2 = r ^ 2 \\ \ end {array}$$

Di sini perlu dicatat bahwa r dapat bervariasi dari 0 hingga + ∞, karena x bervariasi dalam kisaran yang sama. Tetapi sudut φ bervariasi dari 0 hingga π / 2, yang menggambarkan wilayah integrasi pada kuartal pertama sistem koordinat Cartesian. Mengganti dalam sumber, kita mendapatkan:

$$

$$\ begin {array} {l} I ^ 2 = \ int \ limit_0 ^ \ infty {\ int \ limit_0 ^ \ infty {e ^ {- \ kiri ({x ^ 2 + y ^ 2} \ kanan)}} } dxdy = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ int \ limit_0 ^ \ infty {e ^ {- r ^ 2}}} rd \ varphi dr = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limit_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ kiri ({r ^ 2} \ kanan)} = \\ = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ kiri ({\ kiri. {- e ^ {- r ^ 2}} \ kanan | _0 ^ \ infty} \ kanan) = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ kiri ({- e ^ {- \ infty} - \ kiri ({ - e ^ 0} \ kanan)} \ kanan) = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \ kiri ({\ kiri. \ varphi \ kanan | _0 ^ {\ frac {\ pi} {2}}} \ kanan) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Karena simetri integral dan rentang nilai positif dari integrand, kita dapat menyimpulkan itu

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Mari kita cari beberapa solusi lagi? Ini menarik! :)

Pertimbangkan fungsinya $$$g \ kiri (t \ kanan) = \ kiri ({1 + t} \ kanan) e ^ {- t}$
Sekarang mari kita mengingat matematika sekolah dan melakukan studi sederhana dari suatu fungsi menggunakan turunan dan batasan. Bukannya kita akan mempertimbangkan batasan kompleks di sini (setelah semua, mereka tidak lulus di sekolah), kita hanya membahas apa yang akan terjadi pada fungsi jika argumennya cenderung nol atau hingga tak terbatas, sehingga kita akan memperkirakan perilaku asimptotik, yang selalu sangat penting dalam matematika. Ini seperti penilaian kualitatif tentang apa yang terjadi.

$$

$$\ begin {array} {l} g \ kiri (t \ kanan) = \ kiri ({1 + t} \ kanan) e ^ {- t} \\ g '\ kiri (t \ kanan) = e ^ { - t} - \ kiri ({1 + t} \ kanan) e ^ {- t} = - te ^ {- t} \\ g '\ kiri (t \ kanan) = 0 \ ke t = 0 \\ \ kiri [\ begin {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ kiri (t \ kanan) - {\ rm {meningkat}} \\ t> 0 \ to - te ^ {- t} <0 \ to g \ kiri (t \ kanan) - {\ rm {menurun}} \\ \ end {array} \ kanan. \\ g \ kiri (0 \ kanan) = \ kiri ({1 + 0} \ kanan) e ^ {- 0} = 1 \\ g \ kiri ({- 1} \ kanan) = \ kiri ({1 - 1} \ kanan) e ^ {- \ kiri ({- 1} \ kanan)} = 0 \\ g \ kiri (\ infty \ kanan) = \ kiri ({1 + \ infty} \ kanan) e ^ {- \ infty} = 0 \\ \ end {array}$$

Itu dibatasi di atas oleh kesatuan pada interval (-∞; + ∞) dan nol pada interval [-1; + ∞).

Kami membuat perubahan variabel berikut $$$t = \ pm x ^ 2$
Dan kita mendapatkan:

$$

$$t = \ pm x ^ 2 \ ke \ kiri \ {\ begin {array} {l} 0 <\ kiri ({1 - x ^ 2} \ kanan) e ^ {x ^ 2} <1 \\ 0 < \ kiri ({1 + x ^ 2} \ kanan) e ^ {- x ^ 2} <1 \\ \ end {array} \ kanan. \ ke \ kiri \ {\ mulai {array} {l} 0 <\ kiri ({1 - x ^ 2} \ kanan) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ benar.$$

Dalam ketidaksetaraan pertama, kami membatasi variasi (0,1), dan pada yang kedua, interval (0; + ∞), kami meningkatkan kedua ketidaksetaraan pada kekuatan n, karena ketidaksetaraan dengan istilah positif dapat dinaikkan ke tingkat positif apa pun. Kami mendapatkan:

$$

$$\ begin {array} {* {20} c} {\ kiri \ {\ begin {array} {l} \ kiri ({1 - x ^ 2} \ kanan) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ kanan.} & {\ Kiri \ {\ begin {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ kanan) ^ n}} \\ x> 1 \\ \ end {array} \ benar.} \\ \ end {array}$$

Mari kita buat grafik untuk n = 1 untuk menunjukkan ketidaksetaraan

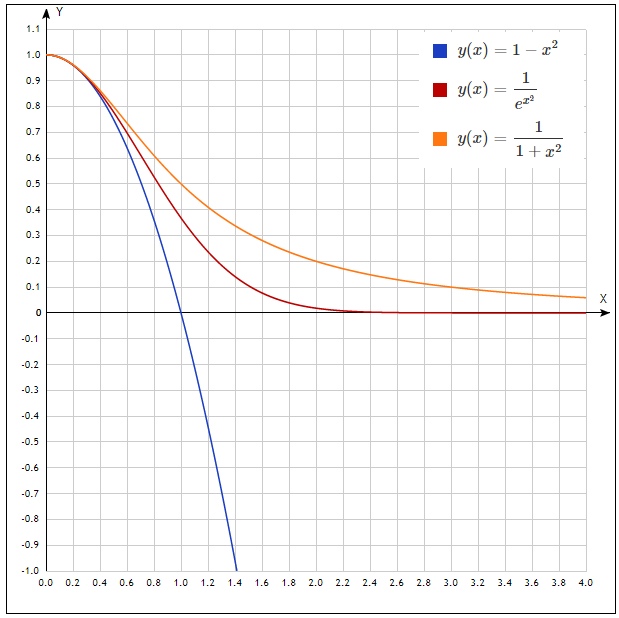
Sekarang kami mencoba untuk mengintegrasikan ketidaksetaraan dalam batas yang ditunjukkan dalam sistem yang sesuai. Dan segera gabungkan semuanya menjadi satu ketimpangan:

$$

$$\ int \ limit_0 ^ 1 {\ kiri ({1 - x ^ 2} \ kanan) ^ n dx} <\ int \ limit_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ infty {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ infty {\ frac {1} {{\ kiri ({1 + x ^ 2} \ kanan) ^ n}} dx}$$

Sekali lagi, jika Anda melihat grafiknya, maka ketidaksetaraan ini benar.

Diberi penggantian kecil, mudah untuk melihat bahwa:

$$

$$\ int \ limit_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ kiri [\ begin {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ frac { {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ kanan] = \ frac {1} {{\ sqrt n}} \ int \ limit_0 ^ \ infty {e ^ {- p ^ 2} dp} = \ frac {1} {{\ sqrt n}} I$$

Yaitu dalam ketimpangan besar di tengah, kita memiliki integral Euler-Poisson, dan sekarang kita perlu menemukan integral yang berdiri di perbatasan ketidaksetaraan ini.

Temukan integral dari batas kiri:

$$

$$\ begin {array} {l} \ int \ limit_0 ^ 1 {\ kiri ({1 - x ^ 2} \ kanan) ^ n dx} = \ kiri [{\ begin {array} {* {20} c} \ begin {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ mulai {array} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ to t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ kanan] = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limit_0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}$$

Untuk menghitung dan mengevaluasinya, pertama mari kita temukan integral umum. Sekarang saya akan menunjukkan kepada Anda bagaimana menurunkan formula reduksi (dalam matematika, dengan rumus seperti itu artinya menurunkan derajat) untuk integral yang diberikan.

$$

$$\ begin {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ kiri ({\ sin t} \ kanan)} = \\ = \ kiri [{\ begin {array} {* { 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ kiri ({n - 1} \ kanan) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ kiri ({\ sin t} \ kanan)} & {v = \ sin t} \\ \ end {array}} \ kanan] = \\ = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ kiri ({1 - \ cos ^ 2 t} \ kanan) dt} = \\ = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}$$

$$

$$\ begin {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt } + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} \\ n \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt = \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ kiri ({n - 1} \ kanan) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt}} \\ \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt = \ frac {1} {n} \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ { n - 2} tdt}} \\ \ end {array}$$

Sekarang, jika menggunakan rumus reduksi kami menganggap integral yang sama, tetapi dengan batas kami dari 0 hingga π / 2, maka kami dapat membuat beberapa penyederhanaan:

$$

$$\ begin {array} {l} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ kiri [{\ frac {1} {n} \ kiri. {\ cos ^ {n - 1} t \ sin t} \ kanan | _0 ^ {\ frac {\ pi} {2}} = 0} \ kanan] = \\ = \ frac {{n - 1}} { n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ kiri ({\ frac {1 } {{n - 2}} \ kiri. {\ cos ^ {n - 3} t \ sin t} \ kanan | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ kanan) = \\ = \ frac {{n - 1 }} {n} \ kiri ({\ frac {{n - 3}} {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ kanan) = \ frac {{n - 1}} {n} \ kiri ({\ frac {{n - 3}} {{n - 2}} \ kiri ({\ frac {{n - 5 }} {{n - 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ kanan)} \ kanan) = \\ = \ frac {{n - 1}} {n} \ kiri ({\ frac {{n - 3}} {{n - 2}} \ kiri ({\ frac {{n - 5}} {{n - 4}} \ kiri ({\ frac {{n - 7}} {{n - 6}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ kanan )} \ kanan)} \ kanan) = ... \\ \ end {array}$$

Seperti yang kita lihat, Anda dapat menurunkannya hingga tak terbatas (tergantung pada n). Namun, ada satu kehalusan. Formula berubah tergantung pada apakah n adalah bilangan genap atau tidak.
Untuk ini, kami mempertimbangkan dua kasus.

$$

$$\ begin {array} {l} n = 10: \\ \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ kiri ({\ frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ kanan) dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ kiri. {\ kiri ({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ kanan)} \ kanan | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\ kiri ({n - 1} \ kanan) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

$$

$$\ begin {array} {l} n = 9: \\ \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} tersisa. {\ kiri ({\ sint} \ kanan)} \ kanan | _0 ^ {\ frac {\ pi} {2}} = \\ = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} { {9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} = \ frac {{\ kiri ({n - 1} \ kanan) !!}} {{n !!}} \\ \ end {array}$$

Dimana n !! - faktorial ganda. Faktor ganda n dilambangkan dengan n !! dan didefinisikan sebagai produk dari semua bilangan asli dalam interval [1, n] yang memiliki paritas yang sama dengan n

Karena kenyataan bahwa 2n +1 adalah angka ganjil untuk nilai n apa pun, kami memperoleh batas kiri ketidaksetaraan kami:

$$

$$\ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ kiri ({2n} \ kanan) !!}} {{\ kiri ({2n + 1} \ kanan) !!}}$$

Temukan integral dari batas kanan:
(di sini kami menggunakan rumus reduksi yang sama dengan yang dibuktikan sebelumnya)

$$

$$\ begin {array} {l} \ int \ limit_0 ^ \ infty {\ frac {1} {{\ kiri ({1 + x ^ 2} \ kanan) ^ n}} dx = \ kiri [\ begin {array } {l} x = \ tan t \ untuk \ begin {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ to t = \ frac {\ pi} {2}} \\ \ end {array} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}} = \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ kanan]} = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2} } {\ cos ^ {2n - 2} tdt} = \ kiri [{\ kiri ({2n - 2} \ kanan) - {\ rm {even}}} kanan] = \ frac {{\ kiri ({2n - 3} \ kanan) !!}} {{\ kiri ({2n - 2} \ kanan) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Setelah kami memperkirakan sisi kiri dan kanan dari ketidaksetaraan, kami membuat beberapa transformasi untuk mengevaluasi batas-batas sisi kiri dan kanan dari ketidaksetaraan, asalkan n cenderung ∞:

$$

$$\ begin {array} {l} \ frac {{\ kiri ({2n} \ kanan) !!}} {{\ kiri ({2n + 1} \ kanan) !!}} <\ frac {1} { {\ sqrt n}} \ cdot Saya <\ frac {{\ kiri ({2n - 3} \ kanan) !!}} {{\ kiri ({2n - 2} \ kanan) !!}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\ kiri ({2n} \ kanan) !!}} {{\ kiri ({2n + 1} \ kanan) !!}} <I <\ sqrt n \ cdot \ frac {{\ kiri ({2n - 3} \ kanan) !!}} {{\ kiri ({2n - 2} \ kanan) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Kuadratkan kedua sisi ketidaksetaraan:

$$

$$n \ cdot \ frac {{\ kiri ({\ kiri ({2n} \ kanan) !!} \ kanan) ^ 2}} {{\ kiri ({\ kiri ({2n + 1} \ kanan) !! } \ kanan) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ kiri ({\ kiri ({2n - 3} \ kanan) !!} \ kanan) ^ 2}} {{\ kiri ( {\ kiri ({2n - 2} \ kanan) !!} \ kanan) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

Sekarang mari kita lakukan sedikit penyimpangan. Pada 1655, John Wallis (ahli matematika Inggris, salah satu cikal bakal analisis matematika). Mengusulkan formula untuk menentukan angka π. J. Wallis mendatanginya, menghitung luas lingkaran. Produk ini menyatu sangat lambat, oleh karena itu, rumus Wallis tidak banyak berguna untuk perhitungan praktis angka π. Tapi itu bagus untuk mengevaluasi ekspresi kami :)

$$

$$\ pi = \ mathop {\ lim} \ limit_ {n \ to \ infty} \ frac {1} {n} \ kiri [{\ frac {{\ kiri ({2n} \ kanan) !!}} {{ \ kiri ({2n - 1} \ kanan) !!}}} \ kanan] ^ 2$$

Sekarang kita mengubah ketidaksetaraan kita sehingga kita bisa melihat di mana harus mengganti rumus Wallis:

$$

$$\ begin {array} {l} \ frac {{n ^ 2}} {{\ kiri ({2n + 1} \ kanan) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ kiri ({\ kiri ({2n} \ kanan) !!} \ kanan) ^ 2}} {{\ kiri ({\ kiri ({2n - 1} \ kanan) !!} \ kanan) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ kiri ({\ kiri ({2n - 2} \ kanan) !!} \ kanan) ^ 2 }} {{\ kiri ({\ kiri ({2n - 3} \ kanan) !!} \ kanan) ^ 2}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limit_ {n \ hingga \ infty} \ kiri [{\ frac {{n ^ 2}} {{\ kiri ({2n + 1} \ kanan) ^ 2}}} \ kanan] \ cdot \ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ kiri ({\ kiri ({2n} \ kanan) !!} \ kanan ) ^ 2}} {{\ kiri ({\ kiri ({2n - 1} \ kanan) !!} \ kanan) ^ 2}}} \ kanan] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limit_ {n \ hingga \ infty} \ kiri [{\ frac {1} {n} \ cdot \ frac {{\ kiri ({\ kiri ({2n - 2} \ kanan) !!} \ kanan) ^ 2}} {{\ kiri ({\ kiri ({2n - 3} \ kanan) !!} \ kanan) ^ 2}}} \ kanan]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ to \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Ini mengikuti dari rumus Wallis bahwa ekspresi kiri dan kanan cenderung π / 4 sebagai n → ∞
Karena fakta bahwa fungsi exp [-x²] adalah genap, kami dengan aman menganggapnya

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Untuk pertama kalinya, integral Gaussian satu dimensi dihitung pada 1729 oleh Euler, kemudian Poisson menemukan cara sederhana untuk menghitungnya. Dalam hal ini, itu disebut integral Euler - Poisson.

Mari kita coba hitung integral Gaussian. Itu dapat ditulis dalam berbagai bentuk. Lagi pula, tidak ada yang mengubah nama variabel tempat integrasi dilakukan.

$$

$$\ begin {array} {l} I = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ Limit_ {- \ infty} ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- z ^ 2} dz} \\ \ end {array}$$

Anda dapat beralih dari Cartesian tiga dimensi ke koordinat bola dan mempertimbangkan kubus integral Gauss.

$$

$$\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {array} \ benar. \ to x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2$$

Jacobian dari transformasi ini dapat dihitung sebagai berikut:

$$

$$\ begin {array} {l} J = \ left | {\ begin {array} {* {20} c} {\ frac {{\ partial x}} {{\ partial r}}} & {\ frac {{\ partial x}} {{\ partial \ theta}} } & {\ frac {{\ partial x}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial y}} {{\ partial r}}} & {\ frac {{\ partial y }} {{\ partial \ theta}}} & {\ frac {{\ partial y}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial z}} {{\ partial r}} } & {\ frac {{\ partial z}} {{\ partial \ theta}}} & {\ frac {{\ partial z}} {{\ partial \ varphi}}} \\ \ end {array}} \ \ benar | = \ kiri | {\ begin {array} {* {20} c} {\ sin \ theta \ cos \ varphi} & {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} & {r \ cos \ theta \ sin \ varphi} & {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} & {- r \ sin \ theta} & 0 \\ \ end {array}} \ kanan | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ begin {array} {l} I ^ 3 = \ int \ limit_ {- \ infty} ^ \ infty {\ int \ limit_ {- \ infty} ^ \ infty {\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ Limit_0 ^ {2 \ pi} {\ int \ Limit_0 ^ \ pi {\ int \ limit_0 ^ \ infty { e ^ {- r ^ 2} Jdrd \ theta d} \ varphi =}} \\ \\ = \ int \ limit_0 ^ {2 \ pi} {d \ varphi} \ int \ limit_0 ^ \ pi {\ sin \ theta d \ theta} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {array}$$

Kami menghitung integral secara berurutan, dimulai dengan yang integral.

$$

$$\ begin {array} {l} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ kiri [\ begin {array} {l} u = r \ untuk du = dr \\ dv = re ^ {- r ^ 2} dr \ to v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {array} \ kanan] = \\ = \ kiri. {\ kiri ({- \ frac {1} {2} re ^ {- r ^ 2}} \ kanan)} \ kanan | _0 ^ \ infty + \ frac {1} {2} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limit_0 ^ \ pi {\ sin \ theta d \ theta} = \ kiri. {\ kiri ({- \ cos \ theta} \ kanan)} \ kanan | _0 ^ \ pi = \ kiri ({- \ cos \ pi} \ kanan) - \ kiri ({- \ cos 0} \ kanan) = 1 + 1 = 2 \\ \ int \ Limit_0 ^ {2 \ pi} {d \ varphi} = \ kiri. \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {array}$$

Maka sebagai hasilnya kita dapatkan:

$$

$$\ begin {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ to I ^ 3 = \ pi I \ to I ^ 2 = \ pi \ to I = \ sqrt \ pi \\ I = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {array}$$

Integral Euler-Poisson sering digunakan dalam teori probabilitas.

Saya berharap bahwa untuk seseorang artikel ini akan bermanfaat dan membantu untuk memahami beberapa teknik matematika :)