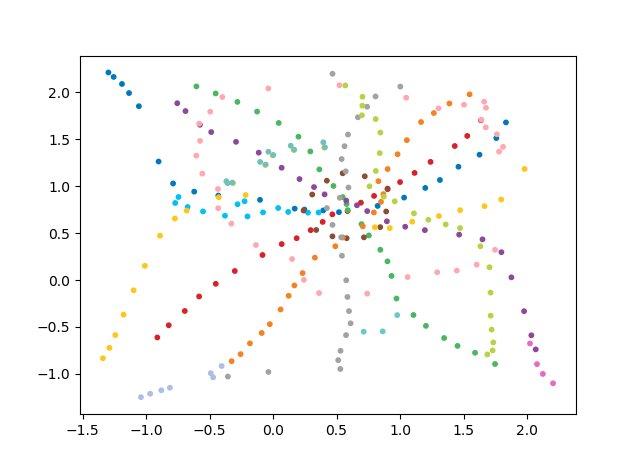
UPD: Seperti yang diminta dalam komentar, saya menambahkan tautan ke skema bergulir Javascript
Sayangnya, kode javascript tidak dapat dimasukkan ke dalam tubuh posting
Selamat siang Baru-baru ini saya membaca sebuah blog dari seorang urbanis yang sedang mendiskusikan seperti apa skema metro ideal itu. Skema metro dapat ditarik berdasarkan dua prinsip:
- Sirkuit harus nyaman dan mudah diingat dan diorientasikan.
- Skema harus sesuai dengan geografi kota
Jelas, prinsip-prinsip ini saling eksklusif dan prinsip pertama membutuhkan distorsi signifikan dari realitas geografis.
Cukup untuk mengingat seperti apa skema metro Moskow dengan cincin dan garis lurus yang indah:
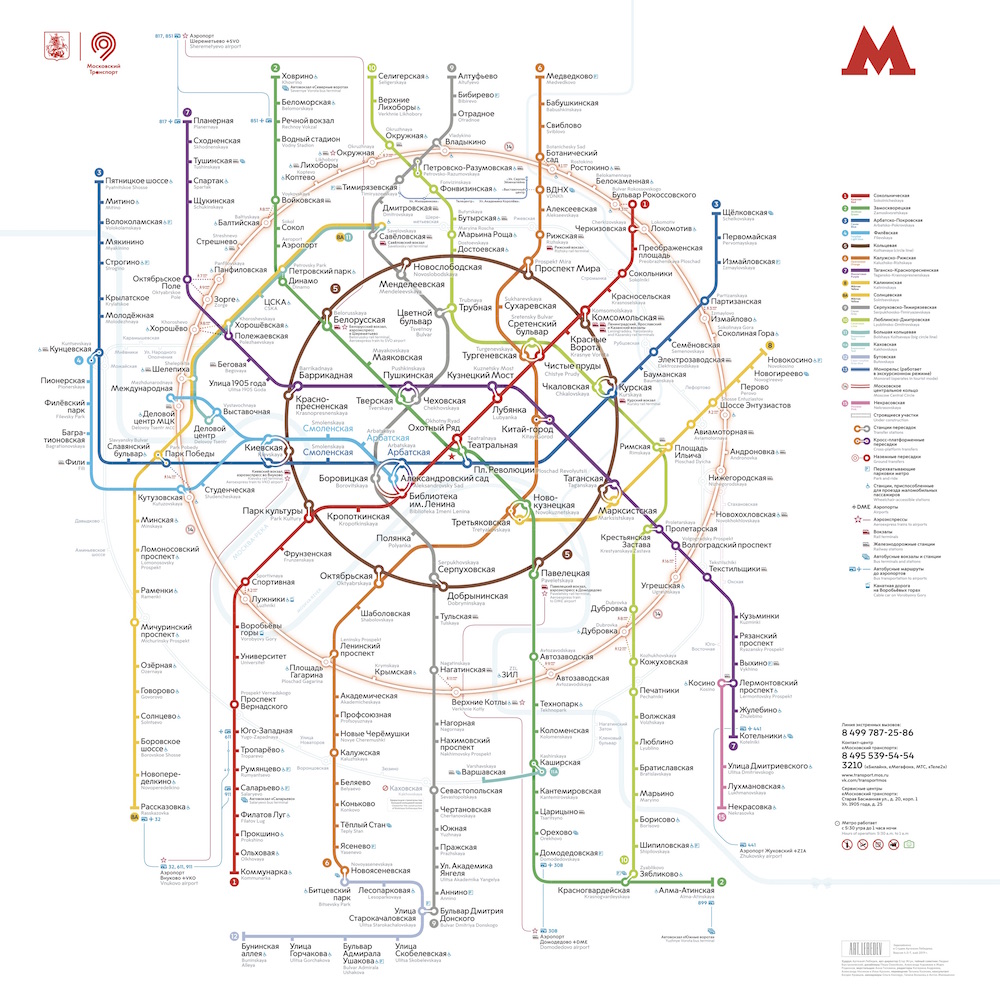
dan bandingkan dengan rencana yang akurat secara geografis:

Rencana tersebut menunjukkan bahwa cincin-cincin itu sama sekali tidak sepenuhnya mulus dan konsentris, garis-garis menekuk lebih dari pada skema, dan kepadatan stasiun di pusat kota sangat tinggi sehingga hampir mustahil untuk mengetahui rencana.
Dan meskipun gambar kedua mencerminkan kenyataan jauh lebih akurat, jelas bahwa lebih nyaman menggunakan skema pertama untuk merencanakan rute di metro.
Dan kemudian pikiran berikut muncul di benak saya: "Akan seperti apa metro jika kriteria untuk membangun sirkuit adalah waktu yang diperlukan untuk berpindah dari satu stasiun ke stasiun lainnya?" Artinya, jika Anda dapat pergi dari satu stasiun ke stasiun lain dengan cepat, maka secara spasial mereka akan berada di dekat Anda pada diagram.
Jelas, dalam ruang dua dimensi tidak mungkin untuk menggambar skema seperti itu di mana jarak antara dua stasiun akan sama dengan waktu tempuh dari satu ke yang lain karena topologi kompleks dari metro metro.
Ada juga firasat bahwa ini sangat mungkin ketika membangun skema di ruang dengan dimensi tinggi (estimasi atas adalah n-1, di mana n adalah jumlah stasiun). Untuk ruang dengan sejumlah kecil dimensi, skema semacam itu hanya dapat dibangun kira-kira.
Tugas membangun peta metro berdasarkan waktu perjalanan terlihat seperti tugas pengoptimalan biasa.
Misalkan kita memiliki set awal koordinat semua stasiun (X, Y, Z) dan matriks target kali berpasangan (jarak). Dimungkinkan untuk membangun metrik "salah" dari sekumpulan koordinat yang diberikan dan kemudian menguranginya dengan metode gradient descent untuk masing-masing koordinat setiap stasiun. Sebagai metrik, kita dapat mengambil fungsi sederhana dari standar deviasi jarak.
Nah, satu-satunya yang tersisa adalah untuk mendapatkan data tentang berapa banyak waktu yang harus dihabiskan untuk bepergian dari stasiun metro Moskow ke stasiun lainnya.
Pikiran pertama adalah untuk memeriksa api metro Yandex dan mendapatkan data ini dari sana. Sayangnya, deskripsi api tidak dapat ditemukan. Tonton waktu secara manual dalam aplikasi untuk waktu yang lama (ada 268 stasiun di metro dan ukuran matriks waktu adalah 268 * 268 = 71824). Karena itu, saya memutuskan untuk memahami sumber data Yandex Metro. Karena tidak ada akses ke server, file apk dengan aplikasi telah diunduh dan data yang diperlukan ditemukan. Semua informasi tentang metro sangat terstruktur dan disimpan dalam format JSON dalam folder arsip aset / metrokit / apk. Semua data disimpan dalam struktur cukup jelas. Meta.json berisi informasi tentang kota-kota yang memiliki skema dalam aplikasi, serta id dari skema ini.
{ "id": "sc77792237", "name": { "en": "Nizhny Novgorod", "ru": " ", "tr": "Nizhny Novgorod", "uk": "і " }, "size": { "packed": 30300, "unpacked": 145408 }, "tags": [ "published" ], "aliases": [ "nizhny-novgorod" ], "logoUrl": "https://avatars.mds.yandex.net/get-bunker/135516/f2f0e33d8def90c56c189cfb57a8e6403b5a441c/orig", "version": "2c27fe1", "geoRegion": { "delta": { "lat": 0.168291, "lon": 0.219727 }, "center": { "lat": 56.326635, "lon": 43.992153 } }, "countryCode": "RU", "defaultAlias": "nizhny-novgorod" }
Dengan id skema, kami menemukan folder dengan JSON terkait dengan Moskow.
File data.json berisi informasi dasar tentang grafik metro, termasuk nama-nama node dari grafik, ID node, koordinat geografis dari node, informasi tentang transisi dari satu stasiun ke stasiun lain (id, waktu transisi, jenis transisi - apakah mengemudi atau berjalan, di jalan atau tidak, waktu Kami tertarik pada detik) dan juga banyak informasi tambahan tentang pintu masuk dan keluar dari stasiun. Ini cukup mudah untuk diketahui. Mari kita mulai menulis kode untuk membangun sirkuit kita.
Kami mengimpor perpustakaan yang diperlukan:
import numpy as np import json import codecs import networkx as nx import matplotlib.pyplot as plt import pandas as pd import itertools import keras import keras.backend as K from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.mplot3d.proj3d import proj_transform from matplotlib.text import Annotation import pickle
Struktur kamus dan daftar python sepenuhnya konsisten dengan struktur format json, jadi kami membaca informasi metro dan membuat objek yang sesuai dengan objek json.
names = json.loads(codecs.open( "l10n.json", "r", "utf_8_sig" ).read() ) graph = json.loads(codecs.open( "data.json", "r", "utf_8_sig" ).read() )
Kami membuat kamus yang memetakan simpul grafik dan stasiun (ini diperlukan karena stasiun ditugaskan untuk nama, bukan simpul grafik)
Juga, untuk berjaga-jaga, kami akan menyimpan koordinat node untuk kemungkinan membangun peta geografis (dinormalisasi ke kisaran 0-1)
nodeStdict={} for stop in graph['stops']['items']: nodeStdict[stop['nodeId']]=stop['stationId'] coordDict={} for node in graph['nodes']['items']: coordDict[node['id']]=(node['attributes']['geoPoint']['lon'],node['attributes']['geoPoint']['lat']) lats=[] longs=[] for value in coordDict.values(): lats.append(value[1]) longs.append(value[0]) for k,v in coordDict.items(): coordDict[k]=((v[0]-np.min(longs))/(np.max(longs)-np.min(longs)),(v[1]-np.min(lats))/(np.max(lats)-np.min(lats)))
Buat grafik metro dengan koneksi. Kami mengatur bobot setiap koneksi. Berat sesuai dengan waktu tempuh. Kami akan menghapus node yang bukan stasiun (menurut saya, ini keluar dari metro dan koneksi ke mereka diperlukan untuk kartu Yandex saat menghitung waktu, tetapi tidak memahaminya dengan tepat), membuat simpul id kamus - nama asli dalam bahasa Rusia
G=nx.Graph() for node in graph['nodes']['items']: G.add_node(node['id'])
Kami mendefinisikan cabang mana (id cabang mana) yang dimiliki masing-masing simpul (ini akan dibutuhkan nanti untuk mewarnai jalur metro dalam diagram)
def getlines(graph, G): nodetoline={} id_from={} id_to={} for lk in graph['tracks']['items']: id_from[lk['id']]=lk['fromNodeId'] id_to[lk['id']]=lk['toNodeId'] for line in graph['linesToTracks']['items']: if line['trackId'] in id_from.keys(): nodetoline[id_from[line['trackId']]]=line['lineId'] nodetoline[id_to[line['trackId']]]=line['lineId'] return nodetoline lines=getlines(graph,G)
Pustaka networkx memungkinkan Anda menemukan panjang jalur terpendek dari satu node ke node lainnya menggunakan fungsi nx.shortest_path_length (G, id1, id2, weight = 'length'), sehingga kami dapat mengasumsikan bahwa kami telah menyelesaikan persiapan data. Hal selanjutnya yang harus dilakukan adalah menyiapkan model yang akan mengoptimalkan koordinat stasiun.
Untuk melakukan ini, kita akan mencari tahu apa yang akan diberikan pada input, ke output, dan bagaimana kita akan mengoptimalkan matriks koordinat stasiun.
Misalkan kita memiliki matriks semua koordinat (3x268). Mengalikan vektor satu-panas (vektor di mana 0 ada di mana-mana kecuali satu unit koordinat di tempat n) dimensi 268 oleh matriks koordinat ini akan memberikan 3 koordinat yang sesuai dengan stasiun n. Jika kita mengambil sepasang vektor satu-panas dan mengalikannya dengan matriks yang diperlukan, kita mendapatkan dua kali lipat koordinat. Dari sepasang koordinat Anda dapat menghitung jarak Euclidean antar stasiun. Dengan demikian, kita dapat menentukan arsitektur model kita:
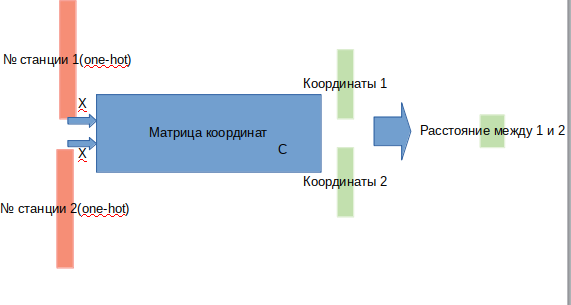
di pintu masuk kami memberikan beberapa stasiun, pada output kami mendapatkan jarak di antara mereka.
Setelah kami memutuskan format data untuk pelatihan model, kami akan menyiapkan data menggunakan pencarian jarak jauh pada grafik:
myIDs=list(G.nodes()) listofinputs1=[] listofinputs2=[] listofoutputs=[] for pair in itertools.product(G.nodes(), repeat=2): vec1=np.zeros((len(myIDs))) vec2=np.zeros((len(myIDs))) vec1[myIDs.index(pair[0])]=1 vec2[myIDs.index(pair[1])]=1 listofinputs1.append(vec1) listofinputs2.append(vec2)
Kami mengoptimalkan matriks koordinat stasiun menggunakan metode gradient descent.
Jika kita menggunakan kerangka keras untuk pembelajaran mesin, kita mendapatkan yang berikut:
np.random.seed(0) initweightmatrix=np.zeros((len(myIDs),3)) for i in range(len(myIDs)): initweightmatrix[i,:2]=coordDict[myIDs[i]] initweightmatrix[i,2]=np.random.randn()*0.001 def euclidean_distance(vects): x, y = vects sum_square = K.sum(K.square(x - y), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon())) def eucl_dist_output_shape(shapes): shape1, shape2 = shapes return (shape1[0], 1) inp1=keras.layers.Input((len(myIDs),)) inp2=keras.layers.Input((len(myIDs),)) layer1=keras.layers.Dense(3,use_bias=None, activation=None) x1=layer1(inp1) x2=layer1(inp2) x=keras.layers.Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([x1, x2]) out=keras.layers.Dense(1,use_bias=None,activation=None)(x) model=keras.Model(inputs=[inp1,inp2],outputs=out) model.layers[2].set_weights([initweightmatrix]) model.layers[2].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
perhatikan bahwa kita menggunakan koordinat geografis nyata sebagai koordinat awal pada layer1 - ini diperlukan agar tidak jatuh ke minimum lokal dari fungsi standar deviasi. Kami menginisialisasi koordinat ketiga ke non-nol untuk mendapatkan gradien non-nol (jika pada awalnya peta benar-benar datar, pergeseran dari setiap stasiun ke atas atau ke bawah akan sama, oleh karena itu gradiennya adalah 0 dan z tidak akan dioptimalkan). Elemen terakhir dari model kami (Dense (1)) memengaruhi penskalaan skema agar sesuai dengan timeline.
Kami akan mengukur jarak dalam hitungan jam, bukan detik, karena urutan jarak sekitar 1 jam, dan untuk pelatihan model yang lebih efektif, penting bahwa semua nilai (input data, bobot, target) kira-kira sama dengan urutan besarnya. Jika nilai-nilai ini dekat dengan 1, maka Anda dapat menggunakan nilai langkah standar untuk optimasi (0.001-0.01).
Line model.layers [2] .trainable = False membekukan koordinat stasiun dan pada tahap pertama satu parameter bervariasi - skala. Setelah memilih skala skema kami, kami mencairkan koordinat dan sudah mengoptimalkannya:
hist=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200) model.layers[2].trainable=True model.layers[-1].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse') hist2=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
kita melihat bahwa kita memberi makan semua pasangan stasiun sekaligus, di pintu keluar semua jarak dan optimisasi kami adalah turunan gradien batch penuh (satu langkah pada semua data). Fungsi kerugian dalam kasus ini adalah deviasi standar, dan Anda dapat melihat bahwa itu adalah 0,015 pada akhir pelatihan, yang berarti deviasi standar kurang dari 1 menit untuk setiap pasangan stasiun. Dengan kata lain, skema yang dihasilkan memungkinkan Anda untuk mengetahui secara akurat jarak yang diperlukan untuk pergi dari satu stasiun ke stasiun lain dengan jarak dalam garis lurus antara stasiun dengan akurasi + -1 menit!
Tapi mari kita lihat seperti apa sirkuit kita!
dapatkan koordinat stasiun, ambil kode warna garis dan buat gambar 3d dengan tanda tangan (kode untuk tampilan tanda tangan yang indah diambil
dari sini ):
class Annotation3D(Annotation): '''Annotate the point xyz with text s''' def __init__(self, s, xyz, *args, **kwargs): Annotation.__init__(self,s, xy=(0,0), *args, **kwargs) self._verts3d = xyz def draw(self, renderer): xs3d, ys3d, zs3d = self._verts3d xs, ys, zs = proj_transform(xs3d, ys3d, zs3d, renderer.M) self.xy=(xs,ys) Annotation.draw(self, renderer) def annotate3D(ax, s, *args, **kwargs): '''add anotation text s to to Axes3d ax''' tag = Annotation3D(s, *args, **kwargs) ax.add_artist(tag) fincoords=model.layers[2].get_weights() ccode={} for obj in graph['services']['items']: ccode[obj['id']]=('\#'+obj['attributes']['color'])[1:] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') for j, xyz_ in enumerate(xyzn): annotate3D(ax, s=labels[myIDs[j]], xyz=xyz_, fontsize=9, xytext=(-3,3), textcoords='offset points', ha='right',va='bottom') plt.show()
Karena ada kesulitan dengan konversi ke format 3d interaktif untuk browser, saya memposting gif:
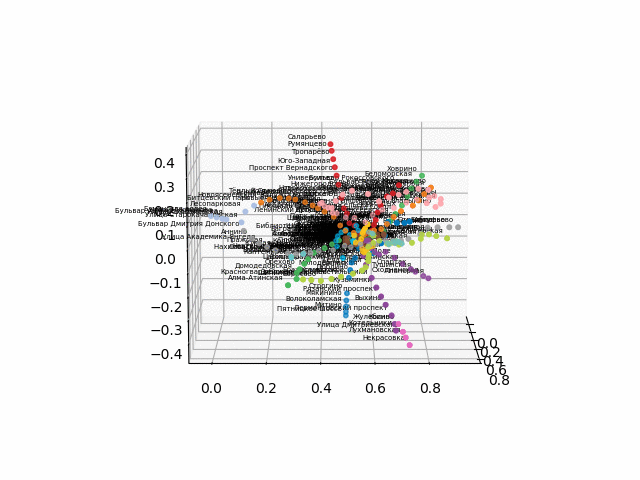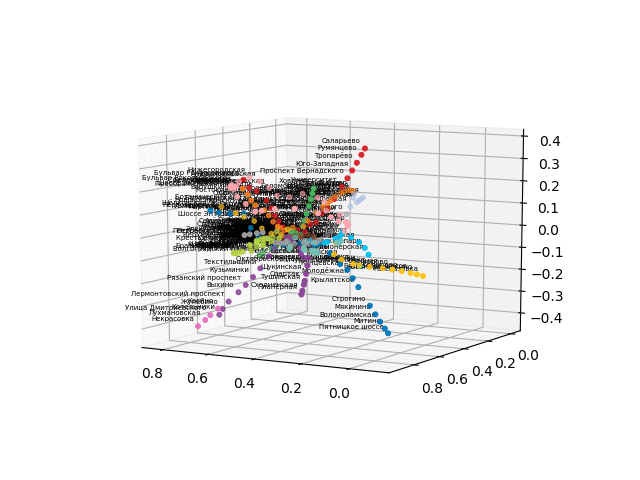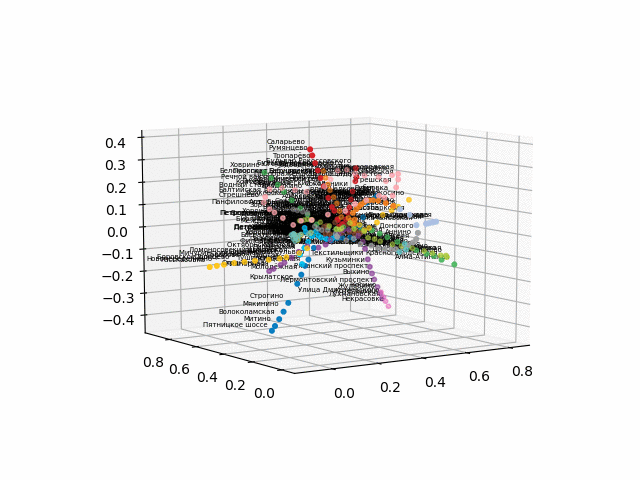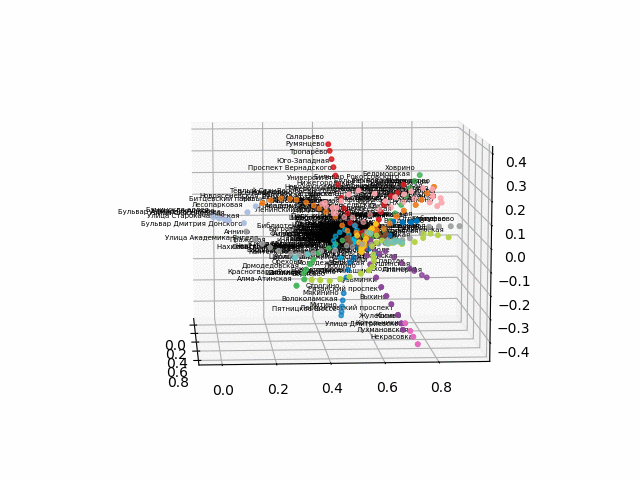
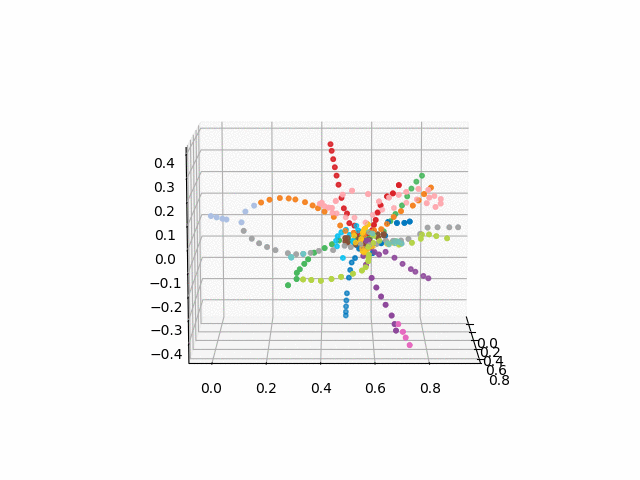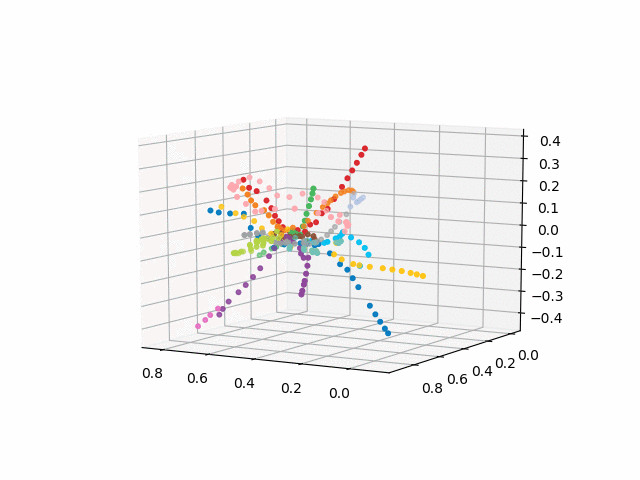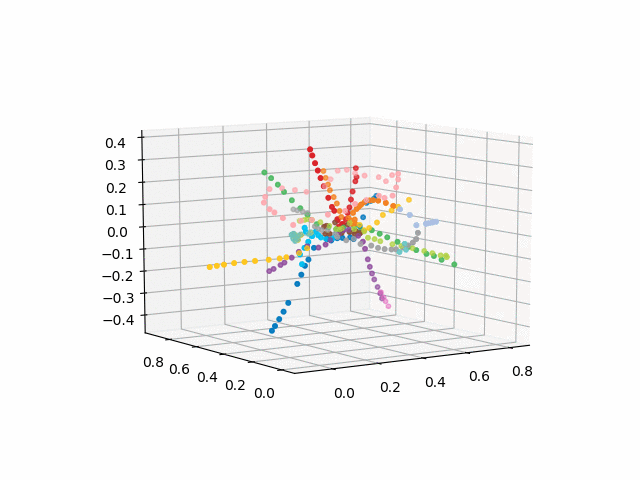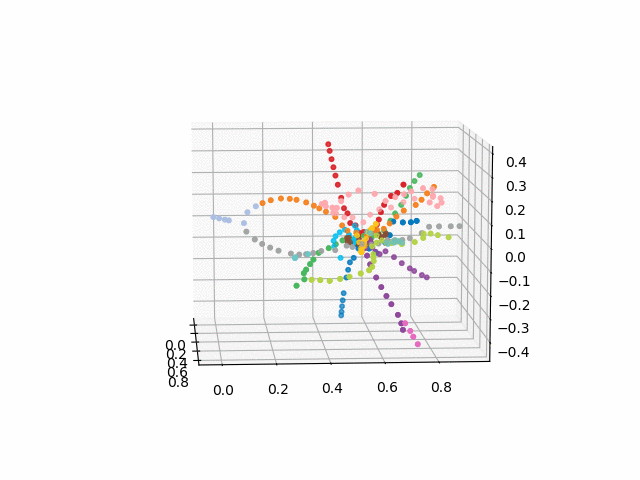
versi tanpa teks terlihat lebih indah dan mudah dikenali:
xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') plt.show()
UPD: Tambahkan jalur metro dengan warna yang diinginkan dan buat gif. Garis hitam - transisi antar stasiun:
myedges=[(myIDs.index(edge[0]),myIDs.index(edge[1]))for edge in G.edges] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] c=[ccode[lines[idi]] for idi in myIDs] fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(x,y,z, c=c, marker='o',s=25) for edge in myedges: col='black' if c[edge[0]]==c[edge[1]]: col=c[edge[0]] ax.plot3D([x[edge[0]], x[edge[1]]], [y[edge[0]], y[edge[1]]], [z[edge[0]], z[edge[1]]], col) ims = [] def rotate(angle): ax.view_init(azim=angle) rot_animation = animation.FuncAnimation(fig, rotate, frames=np.arange(0, 362, 3), interval=70) rot_animation.save('rotation2.gif', dpi=80, writer=matplotlib.animation.PillowWriter(80))
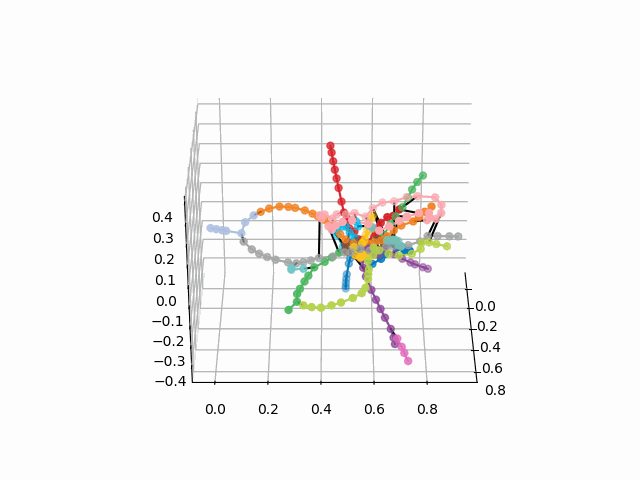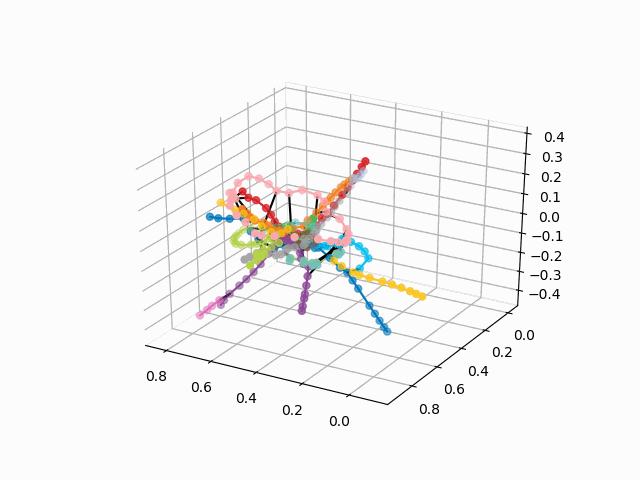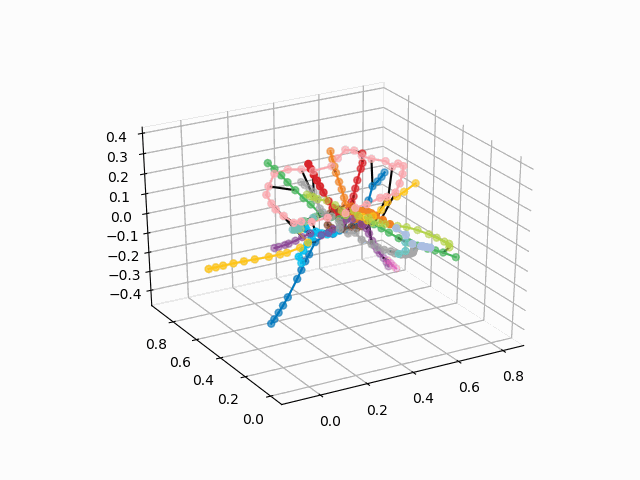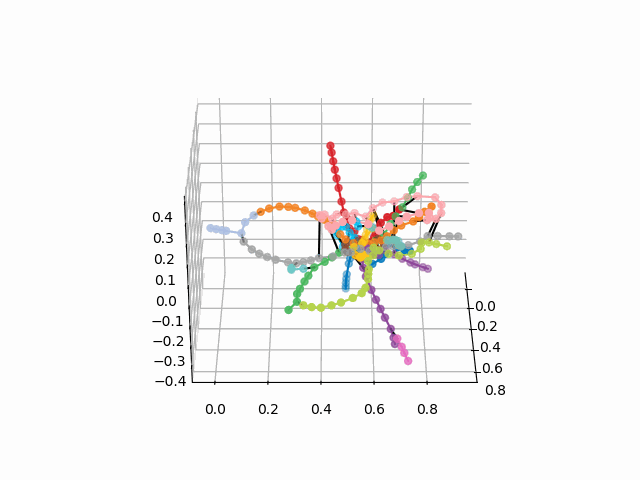
Dari skema ini, beberapa kesimpulan menarik dapat ditarik yang tidak begitu jelas dari skema lain. Untuk beberapa cabang, misalnya, hijau, biru atau ungu, PKS (cincin merah muda) hampir tidak berguna karena transplantasi yang tidak nyaman, yang dapat dilihat pada jarak cincin dari cabang-cabang ini. Rute terpanjang - dari apartemen komunal ke jalan raya gertakan atau Jumat (kuda merah dan merah muda / biru), rute panjang juga merupakan penuturan kisah Alma-Ata dan Bunin Alley-Nekrasovka. Dilihat oleh rencana itu, di utara Moskow ada duplikasi parsial cabang abu-abu dan hijau muda - mereka ada di dekatnya dalam diagram. Akan menarik untuk melihat bagaimana jalur baru (WDC, BKL) dan siapa yang akan lebih sering menggunakannya. Bagaimanapun, saya berharap skema tersebut dapat menjadi alat yang menarik untuk analisis, inspirasi dan perencanaan perjalanan.
PS 3D tidak diperlukan, untuk versi 2D cukup untuk sedikit memperbaiki kode. Tetapi dalam kasus skema 2d, tidak mungkin untuk mencapai keakuratan jarak seperti itu.