🎨 🐯 💞 Metode kuasi-Newtonian, atau ketika ada terlalu banyak turunan kedua untuk Athos ⛏️ 🚸 🦂

Pada kenalan pertama dengan metode kuasi-Newtonian orang mungkin terkejut dua kali. Pertama, setelah melihat sekilas formula, muncul keraguan bahwa ini bisa bekerja sama sekali. Namun, mereka berhasil. Lebih lanjut, tampaknya diragukan bahwa mereka akan bekerja dengan baik. Dan itu jauh lebih mengejutkan untuk melihat seberapa cepat mereka daripada berbagai variasi gradient descent, bukan pada tugas yang dibangun secara khusus, tetapi pada tugas nyata yang diambil dari latihan. Dan jika setelah ini masih ada keraguan dicampur dengan bunga, maka Anda perlu memahami mengapa ini bekerja sama sekali.

Asal dan ide dasar yang menggerakkan metode gradien, termasuk metode Newton, telah dipertimbangkan . Yaitu, kami mengandalkan informasi tentang perilaku fungsi di sekitar posisi saat ini, yang memberi kami analisis matematika sederhana. Minimal, diasumsikan bahwa informasi tentang turunan pertama tersedia untuk kami. Bagaimana jika ini semua yang tersedia bagi kita? Apakah gradient descent kalimat kita? Tentu saja, ya, kecuali jika Anda tiba-tiba ingat bahwa kita sedang berhadapan dengan suatu proses di mana fungsi objektif diproses dengan benar. Dan jika demikian, mengapa kita tidak menggunakan informasi yang terakumulasi tentang perilaku fungsi untuk membuat jalan kita di permukaannya sedikit kurang buta?

Gagasan untuk menggunakan informasi tentang jalan yang dicakup terletak di jantung sebagian besar cara untuk mempercepat metode keturunan. Artikel ini membahas salah satu cara akuntansi yang paling efektif, meskipun bukan yang termurah, untuk informasi semacam ini, yang mengarah ke ide metode kuasi-Newtonian.

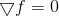
Untuk memahami di mana kaki metode kuasi-Newtonian tumbuh dan dari mana nama itu berasal, kita kembali harus kembali ke metode minimalisasi berdasarkan solusi langsung dari persamaan titik stasioner $"\ bigtriangledown f = 0"$ . Sama seperti pertimbangan metode Newton yang diterapkan pada solusi persamaan ini membawa kita ke metode optimisasi dengan nama yang sama (yang, tidak seperti nenek moyangnya, memiliki wilayah konvergensi global), kita dapat berharap bahwa pertimbangan metode lain untuk menyelesaikan sistem persamaan nonlinear akan bermanfaat dalam rencanakan ide untuk membangun metode optimasi lainnya.

Metode garis potong

Biarkan saya mengingatkan Anda bahwa metode Newton untuk memecahkan sistem persamaan "F (x) = 0"

, didasarkan pada penggantian di lingkungan beberapa titik dekat dengan solusi

fungsi

pendekatan liniernya "L (p) = F (x) + J (x) p"

dimana

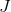
Adalah operator linier, yang, kapan

adalah vektor dan "F"

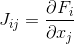
memiliki turunan parsial sehubungan dengan masing-masing variabel, bertepatan dengan matriks Jacobi $"J_ {ij} = \ dfrac {\ partial F_ {i}} {\ partial x_ {j}}"$ . Selanjutnya, persamaan diselesaikan "L (p) = 0"

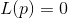
dan titik

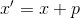
diambil sebagai pendekatan baru ke solusi yang diinginkan. Sederhana dan berhasil.

Tetapi bagaimana jika kita karena suatu alasan tidak dapat menghitung matriks Jacobi? Hal pertama yang terlintas dalam pikiran dalam kasus ini adalah bahwa jika kita tidak dapat menghitung turunan parsial secara analitis, maka kita bisa mendapatkan perkiraan numerik untuknya. 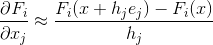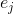Opsi paling sederhana (meskipun bukan satu-satunya) untuk perkiraan seperti itu bisa menjadi rumus perbedaan terbatas yang tepat: $"\ dfrac {\ partial F_ {i}} {\ partial x_ {j}} \ approx \ dfrac {F_ {i} (x + h_ {j} e_ {j}) - F_ {i} (x)} { h_ {j}} "$ dimana $"e_ {j}"$ Apakah vektor basis jth. Matriks yang terdiri dari perkiraan tersebut akan dilambangkan dengan $"\ bar {J}"$ . Analisis berapa banyak penggantian "J"

pada $"\ bar {J}"$ dalam metode Newton, konvergensinya memengaruhi, sejumlah besar karya dikhususkan, tetapi dalam hal ini kami tertarik pada aspek lain. Yaitu, perkiraan seperti itu membutuhkan perhitungan fungsi pada N poin tambahan, dan, di samping itu, fungsi $"\ bar {L} (p) = F (x) + \ bar {J} p"$ pada titik-titik ini interpolasi fungsi "F"

, yaitu

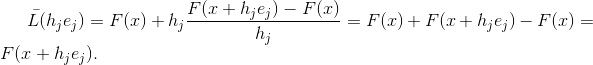
$"\ bar {L (} h_ {j} e_ {j}) = F (x) + h_ {j} \ dfrac {F (x + h_ {j} e_ {j}) - F (x)} {h_ {j}} = F (x) + F (x + h_ {j} e_ {j}) - F (x) = F (x + h_ {j} e_ {j}). "$

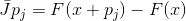
Tidak setiap perkiraan dari matriks Jacobi memiliki properti ini, tetapi setiap matriks dari fungsi affine yang memiliki properti ini adalah perkiraan dari matriks Jacobi. Memang kalau $"F (x + p_ {j}) = F (x) + J (x) p_ {j} + o \ kiri (\ kiri \ Vert p_ {j} \ kanan \ Vert ^ {2} \ kanan)"$ dan $"\ bar {J} p_ {j} = F (x + p_ {j}) - F (x)"$ lalu pada $"\ left \ Vert p_ {j} \ kanan \ Vert \ rightarrow0 \ quad \ bar {J} (x) p_ {j} \ rightarrow J (x) p_ {j}"$ . Properti ini, yaitu, properti interpolasi, memberi kita cara konstruktif untuk menggeneralisasi metode Newton.

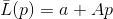
Biarkan $"\ bar {L} (p) = a + Ap"$ - fungsi memenuhi persyaratan $"\ bar {L} (p_ {i}) = F (x + p_ {i})"$ untuk beberapa sistem vektor bebas linear $"p_ {i}"$ . Kemudian fungsi seperti itu disebut fungsi garis potong "F"

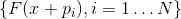
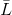
, dan persamaan yang mendefinisikannya adalah persamaan garis potong . Jika sistem vektor $"p_ {i}"$ selesai (yaitu, ada persis N dari mereka dan mereka masih bebas linear), dan, di samping itu, sistem vektor $"\ left \ {F (x + p_ {i}), i = 1 \ dots N \ right \}"$ kemudian bebas linear $"\ bar {L}"$ didefinisikan secara unik.

Metode apa pun berdasarkan perubahan persamaan lokal "F (x) = 0"

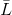
persamaan bentuk $"\ bar {L} (p) = 0"$ dimana $"\ bar {L}"$ memenuhi persamaan garis potong , yang disebut metode garis potong .

Sebuah pertanyaan yang wajar muncul tentang bagaimana membangun garis potong untuk fungsi dengan cara yang paling rasional. "F"

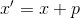
. Garis penalaran berikut nampak jelas: biarkan model affine dibangun pada titik x yang menginterpolasi fungsi yang diberikan pada titik $"x-x_ {1}, x-x_ {2}, \ dots, x-x_ {N}"$ . Solusi persamaan $"\ bar {L} (p) = 0"$ memberi kami poin baru & quot; x '= x + p & quot;

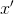
. Kemudian untuk membangun model affine pada suatu titik & quot; x '& quot;

paling masuk akal untuk memilih titik interpolasi sehingga nilainya "F"

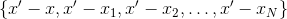
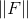
sudah diketahui - yaitu, ambil dari set $& quot; \ kiri \ {x'-x, x'-x_ {1}, x'-x_ {2}, \ dots, x'-x_ {N} \ kanan \} & quot;$ . Ada beberapa opsi untuk memilih poin dari yang sebelumnya banyak digunakan. Misalnya, Anda dapat mengambil titik interpolasi yang ada di dalamnya $"\ kiri \ Vert F \ kanan \ Vert"$ paling tidak penting atau hanya yang pertama "N"

poin. Dalam hal apapun, tampak jelas itu & quot; p = x'-x & quot;

harus dimasukkan dalam banyak titik interpolasi untuk model affine baru. Begitu seterusnya "n"

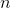
langkah-langkah proses iteratif di set kami bisa sampai "n"

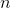
perpindahan dibangun di atas titik-titik yang sebelumnya dilewati. Jika proses dibangun sedemikian rupa sehingga model affine baru tidak lagi digunakan "p"

dari nilai sebelumnya, maka proses seperti itu disebut metode garis potong p-point.

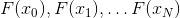
Sekilas, mungkin tampak bahwa metode garis potong N-point adalah kandidat terbaik untuk peran menggantikan metode Newton, karena metode ini memanfaatkan secara maksimal informasi yang kami peroleh dalam proses penyelesaian, sambil meminimalkan jumlah perhitungan tambahan - kami menggunakan fungsi tersebut N poin terlewati. Sayangnya, ini tidak benar. Masalahnya adalah bahwa sistem vektor $"F (x_ {0}), F (x_ {1}), \ dots F (x_ {N})"$ keras kepala menolak untuk mandiri secara linear dengan N. cukup besar. Selain itu, bahkan jika kondisi ini ternyata terpenuhi dan model affine yang sesuai masih ada, maka ada kemungkinan bahwa arah $"p_ {j} = x_ {j} -x_ {0}"$ juga terbukti independen secara linear, ternyata lebih sedikit. Dan ini mensyaratkan fakta bahwa model affine, meskipun ada, merosot dan praktis tidak cocok.

Secara umum, yang paling stabil adalah metode garis potong 2-point. Yaitu, metode di mana pada setiap iterasi kita harus menghitung nilai N-1 fungsi tambahan. Ini jelas tidak cocok untuk tujuan praktis kita.

Lalu pertanyaannya adalah - apa semua ini?

Metode kuasi-Newtonian untuk memecahkan persamaan

Jalan keluarnya sederhana, meski tidak jelas. Jika kita tidak memiliki kemampuan teknis, berdasarkan nilai yang sudah dihitung, untuk secara unik menentukan model affine yang memenuhi persamaan garis potong, maka itu tidak perlu. Kami mengambil persamaan garis potong sebagai dasar, tetapi kami akan mengharuskan persamaan hanya terpenuhi untuk beberapa sistem vektor yang tidak lengkap $"\ kiri \ {p_ {1}, p_ {2}, \ dots, p_ {m} \ kanan \}, m & lt; N"$ . Dengan kata lain, kami akan mensyaratkan bahwa kondisi interpolasi dipenuhi hanya untuk sejumlah kecil nilai yang diketahui. Tentu saja, dalam hal ini kita tidak dapat lagi menjamin bahwa matriks yang digunakan dalam model seperti itu akan cenderung ke matriks Jacobi, tetapi kita tidak akan membutuhkan ini. Menambah ini, model affine harus menginterpolasi fungsi pada titik saat ini, yaitu $"\ bar {L} (0) = F (x)"$ , kami mendapatkan formulasi berikut dari metode garis potong:

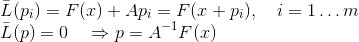
$"\\ \ bar {L} (p_ {i}) = F (x) + Ap_ {i} = F (x + p_ {i}), \ quad i = 1 \ titik m \\ \ bar {L} (p) = 0 \ quad \ Rightarrow p = A ^ {- 1} F (x) "$

Bruiden adalah orang pertama yang mempertimbangkan metode semacam ini untuk m = 1, menyebutnya kuasi-Newtonian. Jelas bahwa kondisi garis potong dalam kasus ini memungkinkan kita untuk mengidentifikasi matriks secara unik "A"

hanya jika kondisi tambahan dikenakan padanya, dan masing-masing kondisi tambahan tersebut menimbulkan metode terpisah. Bruyden sendiri beralasan sebagai berikut:

sebagai gerakan ke arah dari titik $"x_ {0}"$ to the point $"x_ {1}"$ tidak memberi kami informasi tambahan tentang bagaimana fungsi berubah selain arah, maka efek dari fungsi affine baru pada vektor harus berbeda dari efek fungsi lama pada vektor yang sama semakin sedikit semakin berbeda dari . Sebagai pilihan terakhir, kapan ortogonal , perilaku fungsi baru tidak boleh berbeda dari perilaku yang lama.

Ide Breiden brilian dalam kesederhanaannya. Memang, jika kita tidak memiliki informasi baru tentang perilaku fungsi, maka yang terbaik yang bisa kita lakukan adalah berusaha untuk tidak melanggar yang lama. Kemudian syarat tambahan

$"\ bar {L} _ {1} q = \ bar {L} _ {0} q"$ untuk semua

sedemikian rupa $"q ^ {T} p = 0"$

memungkinkan Anda untuk secara unik menentukan matriks dari transformasi baru - ini diperoleh dengan menambahkan koreksi peringkat 1 ke matriks lama.

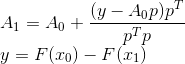
$"\\ A_ {1} = A_ {0} + \ dfrac {(y-A_ {0} p) p ^ {T}} {p ^ {T} p} \\ y = F (x_ {0}) -F (x_ {1}) "$

Namun, terlepas dari kesederhanaan dan konsistensi kesimpulan yang dibuat oleh Bruiden, mereka tidak memberikan titik tumpu yang dapat berfungsi sebagai dasar untuk membangun metode serupa lainnya. Untungnya, ada ungkapan yang lebih formal dari idenya. Yaitu, matriks dibangun dengan cara ini $"A_ {1}"$ Ternyata menjadi solusi untuk masalah berikut:

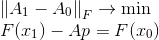
$"\\ \ left \ Vert A_ {1} -A_ {0} \ right \ Vert _ {F} \ rightarrow \ min \\ F (x_ {1}) - Ap = F (x_ {0})"$

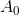
Kendala tugas tidak lain adalah persamaan garis potong, dan kondisi minimalisasi mencerminkan keinginan kami untuk menyimpan informasi sebanyak mungkin dalam matriks $"A_ {0}"$ . Ukuran perbedaan antara matriks dalam kasus ini adalah norma Frobenius, di mana masalah yang ditimbulkan memiliki solusi yang tidak ambigu. Formulasi ini dapat berfungsi sebagai titik awal untuk membangun metode lain. Yaitu, kita dapat mengubah ukuran yang digunakan untuk mengevaluasi perubahan yang diperkenalkan dan memperketat kondisi yang dikenakan pada matriks. Secara umum, seseorang sudah dapat bekerja dengan rumusan metode seperti itu.

Metode Optimasi Kuasi-Newton

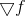
Setelah memahami ide utama, kami akhirnya dapat kembali ke masalah optimisasi dan memperhatikan bahwa menerapkan rumus Bruyden untuk menghitung ulang model affine tidak sesuai dengan tugas kami dengan baik. Bahkan, turunan pertama dari fungsi gradien $"\ bigtriangledown f"$ tidak ada yang lain selain matriks Hessian, yang dengan konstruksi simetris. 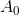Pada saat yang sama, memperbarui menurut aturan Bruyden mengarah ke matriks asimetris $"A_ {1}"$ bahkan jika $"A_ {0}"$ simetris. Ini tidak berarti bahwa metode Bruden tidak dapat diterapkan untuk menyelesaikan persamaan titik stasioner, tetapi berdasarkan pada aturan pembaruan seperti itu, kita tidak mungkin dapat membangun metode optimasi yang baik. Secara umum, cukup jelas bahwa metode quasi-Newton harus bekerja lebih baik, lebih akurat sistem kondisi masalah menggambarkan spesifikasi matriks Jacobi tertentu.

Untuk memperbaiki kekurangan ini, kami menambahkan kendala tambahan untuk masalah minimisasi Bruden, secara eksplisit mensyaratkan bahwa matriks baru simetris bersama dengan yang lama:

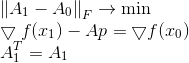
$"\\ \ left \ Vert A_ {1} -A_ {0} \ right \ Vert _ {F} \ rightarrow \ min \\ \ bigtriangledown f (x_ {1}) - Ap = \ bigtriangledown f (x_ {0}} ) \\ A_ {1} ^ {T} = A_ {1} "$

Solusi untuk masalah ini adalah

$"A_ {1} = A_ {0} + \ dfrac {(y-A_ {0} p) p ^ {T} + p (y-A_ {0} p) ^ {T}} {p ^ {T} p} - \ dfrac {(y-A_ {0} p) ^ {T} p} {\ kiri (p ^ {T} p \ kanan) ^ {2}} pp ^ {T} "$

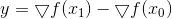
Di sini $y = \ bigtriangledown f (x_ {1}) - \ bigtriangledown f (x_ {0})$ , dan rumus perhitungan ulang matriks dinamai penciptanya - Powell, Shanno dan Bruyden (PSB). Matriks yang dihasilkan simetris, tetapi jelas tidak positif pasti, jika hanya tiba-tiba "y"

tidak akan menjadi linier "p"

. Dan kami melihat bahwa kepastian positif sangat diinginkan dalam metode optimasi.

Sekali lagi, kita akan memperbaiki kondisi masalah, menggunakan kali ini norma Frobenius yang diskalakan sebagai ukuran divergensi matriks.

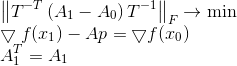
$"\\ \ kiri \ Vert T ^ {- T} \ kiri (A_ {1} -A_ {0} \ kanan) T ^ {- 1} \ right \ Vert _ {F} \ rightarrow \ min \\ \ bigtriangledown f (x_ {1}) - Ap = \ bigtriangledown f (x_ {0}) \\ A_ {1} ^ {T} = A_ {1} "$

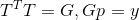
Asal usul pernyataan pertanyaan semacam itu adalah topik besar yang terpisah, tetapi menarik bahwa jika matriks T adalah seperti itu $T ^ {T} T = G, Gp = y$ (yaitu, G juga merupakan matriks transformasi affine yang memenuhi persamaan garis potong untuk arah p), maka solusi untuk masalah ini ternyata tidak tergantung pada pilihan T dan mengarah ke rumus pembaruan

$"A_ {1} = A_ {0} + \ dfrac {(y-A_ {0} p) y ^ {T} + y (y-A_ {0} p) ^ {T}} {y ^ {T} p} - \ dfrac {\ kiri (y-A_ {0} p \ kanan) ^ {T} p} {\ kiri (y ^ {T} p \ kanan) ^ {2}} yy ^ {T} "$

dikenal sebagai rumus Davidon-Fletcher-Powell. Metode pembaruan ini telah terbukti dalam praktiknya, karena memiliki properti berikut:

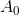jika $"y ^ {T} p & gt; 0"$ dan $"A_ {0}"$ pasti positif $"A_ {1}"$ juga diidentifikasi secara positif.

Saya perhatikan setelah itu jika kondisi pertama tidak terpenuhi, maka tidak ada fungsi affine dengan matriks pasti positif yang memenuhi persamaan garis potong.

Jika dalam masalah yang mengarah ke metode DFP, kami mengambil, sebagai ukuran dari perbedaan model affine, jarak bukan antara matriks itu sendiri, tetapi antara matriks yang terbalik dengan mereka, kami mendapatkan masalah

$"\\ \ kiri \ Vert T ^ {- T} \ kiri (A_ {1} ^ {- 1} -A_ {0} ^ {- 1} \ kanan) T ^ {- 1} \ kanan \ Vert _ { F} \ rightarrow \ min \\ \ bigtriangledown f (x_ {1}) - Ap = \ bigtriangledown f (x_ {0}) \\ A_ {1} ^ {T} = A_ {1} ""$

Solusinya adalah formula terkenal, ditemukan hampir bersamaan oleh Breiden, Fletcher, Goldfarb dan Shanno (BFGS).

$"A_ {1} = A_ {0} + \ dfrac {yy ^ {T}} {y ^ {T} p} - \ dfrac {A_ {0} pp ^ {T} A_ {0}} {p ^ { T} A_ {0} p} "$

Sampai saat ini, diyakini bahwa perhitungan ulang menurut rumus ini adalah yang paling efisien dari sudut pandang komputasi dan pada saat yang sama kurang rentan terhadap degenerasi matriks dengan sejumlah besar iterasi. Di bawah kondisi yang sama seperti DFP, rumus ini menjaga properti definiteness positif.

Semua metode yang dijelaskan untuk memperbarui matriks memerlukan koreksi peringkat 2. Ini membuatnya mudah dan mudah untuk membalikkan matriks $"A_ {1}"$ menggunakan rumus Sherman-Morrison dan nilainya $"A_ {0} ^ {- 1}"$ .

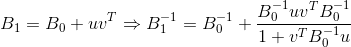
$"B_ {1} = B_ {0} + uv ^ {T} \ Rightarrow B_ {1} ^ {- 1} = B_ {0} ^ {- 1} + \ dfrac {B_ {0} ^ {- 1} uv ^ {T} B_ {0} ^ {- 1}} {1 + v ^ {T} B_ {0} ^ {- 1} u} "$

asalkan penyebut formula tidak nol. Saya tidak akan memberikan formula khusus untuk memperbarui matriks terbalik dari metode yang terdaftar, karena mudah ditemukan atau diturunkan secara independen. Satu-satunya hal yang harus dicatat dalam kasus ini adalah bahwa varian metode dengan memperbarui matriks terbalik biasanya jauh lebih tidak stabil (yaitu, mereka menderita lebih dari kesalahan pembulatan) daripada yang menyarankan memperbarui matriks asli. Paling efektif untuk memperbarui bukan matriks itu sendiri, tetapi dekomposisi Cholesky (kecuali, tentu saja, dekomposisi seperti itu terjadi), karena opsi implementasi seperti itu lebih stabil secara numerik dan, di samping itu, meminimalkan biaya penyelesaian persamaan yang menentukan arah gerak.

Masih mempertimbangkan pertanyaan tentang bagaimana matriks pertama harus terlihat dalam proses kuasi-Newtonian. Semuanya jelas di sini - semakin dekat ke matriks Hessian atau ke versi yang dikoreksi, jika Hessian tiba-tiba tidak berubah menjadi positif pasti, semakin baik dari sudut pandang konvergensi. Namun, pada prinsipnya, setiap matriks pasti positif dapat cocok untuk kita. Versi paling sederhana dari matriks semacam itu adalah satu, dan kemudian iterasi pertama bertepatan dengan iterasi penurunan gradien. Fletcher dan Powell menunjukkan (secara alami, untuk metode DFP) bahwa jika fungsi kuadrat diminimalkan, terlepas dari matriks mana (positif pasti) yang digunakan sebagai iterasi DFP awal, mereka akan mengarah ke solusi dalam iterasi N persis, di mana N adalah dimensi masalah, dan matriks kuasi-Newtonian bertepatan dengan matriks Hessian pada titik minimum. Dalam kasus kebahagiaan seperti itu, kita tentu saja tidak akan menunggu, tetapi ini setidaknya memberi alasan untuk tidak terlalu khawatir tentang pilihan yang buruk dari matriks awal.

Kesimpulan

Pendekatan yang dijelaskan untuk pembangunan metode kuasi-Newtonian bukan satu-satunya yang mungkin. Paling tidak, para penemu dari metode kuasi-Newtonian yang dijelaskan dan banyak peneliti berikutnya sampai pada formula yang sama berdasarkan pertimbangan yang sangat berbeda. Namun, menarik bahwa segera setelah metode kuasi-Newtonian tertentu muncul, maka terlepas dari metode memperolehnya, setelah waktu yang agak singkat menjadi jelas bahwa itu adalah solusi untuk beberapa masalah optimasi yang sangat mudah ditafsirkan. , , , . , , , , , — .

, , , , , , . , , — , - . , , . , . , — .

, . , ( , , N , , ). ( , , ), . , , — . — .

Metode kuasi-Newtonian, atau ketika ada terlalu banyak turunan kedua untuk Athos

Metode garis potong

Metode kuasi-Newtonian untuk memecahkan persamaan

Metode Optimasi Kuasi-Newton

Kesimpulan

More articles: