Di dalam JeMalloc. Struktur Data Inti: Pairing Heap & Bitmap Tree

Tema Allocator sering muncul di Internet: memang, Allocator adalah semacam batu penjuru, jantung dari aplikasi apa pun. Dalam seri posting ini saya ingin berbicara secara rinci tentang satu pengalokasi yang sangat menghibur dan terkemuka - JeMalloc , didukung dan dikembangkan oleh Facebook dan digunakan, misalnya, dalam bionik [Android] lib C.

Di jaringan, saya tidak dapat menemukan detail yang sepenuhnya mengungkapkan jiwa pengalokasi ini, yang pada akhirnya memengaruhi ketidakmungkinan membuat kesimpulan tentang penerapan JeMalloc dalam memecahkan masalah tertentu. Banyak materi keluar dan, agar bisa membacanya tidak melelahkan, saya mengusulkan untuk memulai dengan dasar-dasar: Struktur Data Dasar yang digunakan di JeMalloc.

Di bawah kucing, saya berbicara tentang Pairing Heap dan Bitmap Tree , yang membentuk fondasi JeMalloc. Pada tahap ini, saya tidak menyentuh pada topik multithreading dan Fine Grained Locking , namun, melanjutkan serangkaian posting, saya pasti akan memberi tahu Anda tentang hal-hal ini, untuk itu, pada kenyataannya, berbagai jenis Eksotik dibuat, khususnya yang dijelaskan di bawah ini.

Bitmap_s adalah struktur data mirip pohon yang memungkinkan Anda untuk:

• Cepat menemukan set / unset bit pertama dalam urutan bit yang diberikan.
• Ubah dan dapatkan nilai bit dengan indeks i dalam urutan bit yang diberikan.
• Pohon dibangun berdasarkan urutan n bit dan memiliki properti berikut:
• Unit dasar dari pohon adalah simpul, dan unit dasar dari simpul adalah bit. Setiap node terdiri dari bit k yang tepat. Bitness suatu node dipilih sehingga operasi logis pada rentang bit yang dipilih dihitung secepat dan seefisien mungkin pada komputer yang diberikan. Di JeMalloc, sebuah node diwakili oleh tipe panjang yang tidak ditandai .
• Tinggi pohon diukur dalam level dan untuk urutan n bit adalah H = $$$\ log_ {k} {n} log k (n)$level.
• Setiap tingkat pohon diwakili oleh urutan $$$countOfNodesOnLevel = integerCeil (\ frac {n} {{k} ^ {H - currentLevel + 1}})$node, yang setara dengan urutan $$$countOfBitsOnLevel = countOfNodesOnLevel * k$sedikit.
• Level tertinggi (root) dari pohon terdiri dari k bit, dan terendah - dari n bit.
• Setiap bit dari simpul level L menentukan keadaan semua bit dari simpul anak level L - 1: jika bit diatur ke sibuk, maka semua bit dari simpul anak juga diatur ke sibuk, jika tidak, bit dari simpul anak mungkin memiliki Status 'sibuk' dan 'bebas'.

Adalah masuk akal untuk mewakili bitmap_t dalam dua array: yang pertama, dari dimensi yang sama dengan jumlah semua simpul pohon - untuk menyimpan simpul pohon, dan yang kedua, dari dimensi tinggi pohon - untuk menyimpan offset awal setiap level dalam array node pohon. Dengan metode ini menentukan pohon, elemen root dapat pergi pertama, dan kemudian, secara berurutan, node dari masing-masing level. Namun, penulis JeMalloc menyimpan elemen root terakhir dalam array, dan di depannya adalah node dari level pohon yang mendasarinya.

Sebagai contoh ilustrasi, ambil urutan 92 bit dan K = 32 pikiran. Kami berasumsi bahwa negara bagian 'bebas' - dilambangkan dengan sedikit pun, dan negara 'sibuk' - nol. Asumsikan juga bahwa dalam urutan bit asli, bit dengan indeks 1 (menghitung dari nol, dari kanan ke kiri pada gambar) diatur ke keadaan sibuk. Maka bitmap_t untuk urutan bit seperti itu akan terlihat seperti gambar di bawah ini:



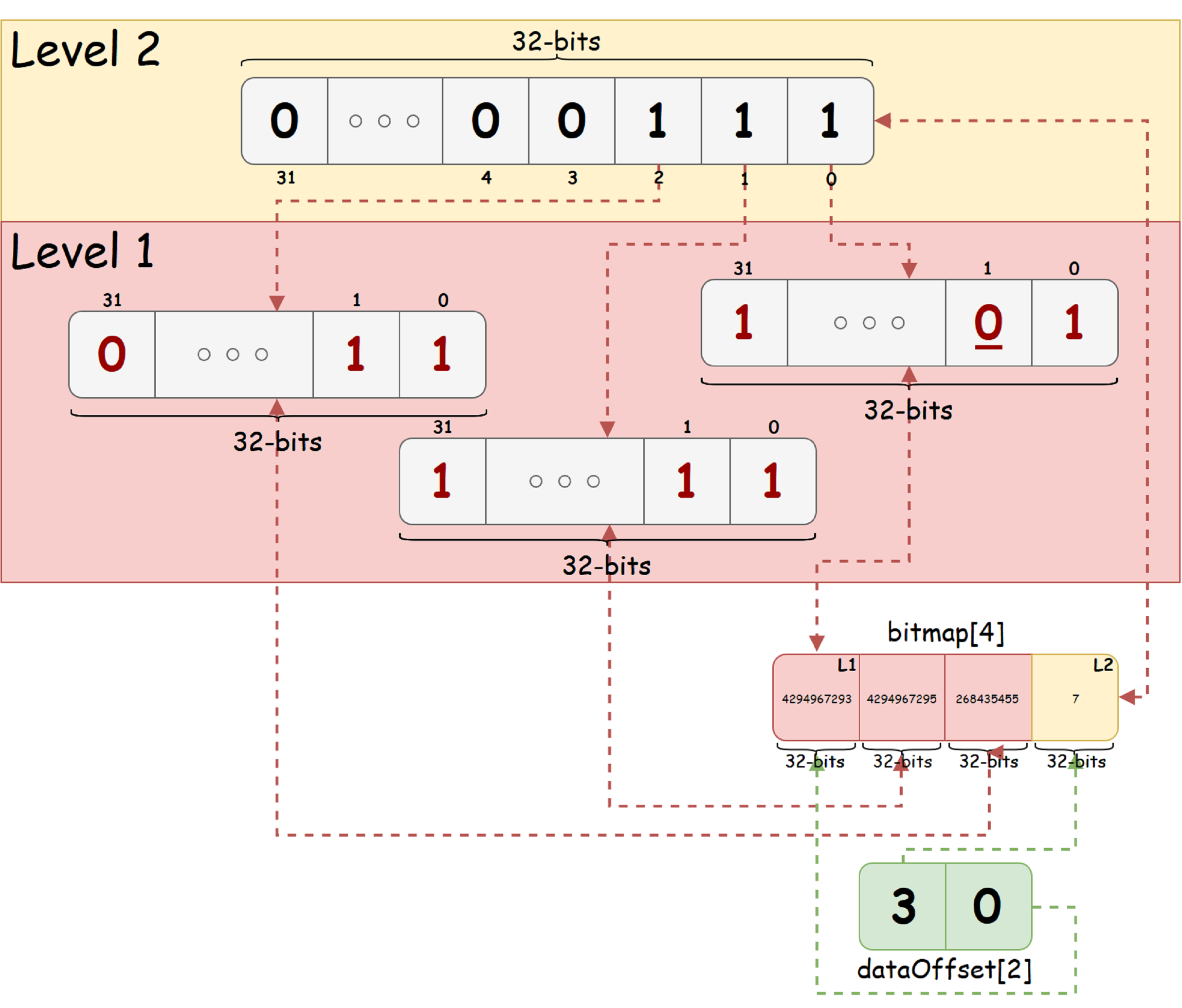Dari gambar tersebut kita melihat bahwa pohon yang dihasilkan hanya memiliki dua tingkat. Level root berisi 3 unit bit, yang menunjukkan keberadaan bit bebas dan yang ditempati di setiap node anak dari bit yang sesuai. Di sudut kanan bawah, Anda dapat melihat tampilan Pohon dalam dua array: semua simpul pohon dan offset dari setiap tingkat dalam array node.

Dengan asumsi bahwa bitmap_t diwakili oleh dua array (array data dan array offset level pohon dalam array data), kami menggambarkan operasi pencarian bit paling signifikan pertama dalam bitmap_t yang diberikan:

• Mulai dari node root, kami melakukan operasi pencarian untuk bit paling signifikan pertama dari node: untuk menyelesaikan masalah ini, prosesor modern memberikan instruksi khusus yang dapat secara signifikan mengurangi waktu pencarian. Kami akan menyimpan hasil yang ditemukan dalam variabel FirstSetedBit .
• Pada setiap iterasi algoritma, kami akan mempertahankan jumlah posisi bit yang ditemukan: countOfSettedBits + = FirstSetedBit
• Dengan menggunakan hasil dari langkah sebelumnya, kita pergi ke simpul anak dari bit satuan paling signifikan pertama dari simpul dan ulangi langkah sebelumnya. Transisi dilakukan sesuai dengan rumus sederhana berikut: $$$currentNode = bitmapData [levelOffsetArray [currentLevel] + sumOfBits]$
• Proses berlanjut hingga tingkat terendah pohon tercapai. countOfSettedBits - jumlah bit yang diinginkan dalam urutan bit input.

Pairing Heap adalah struktur data pohon mirip tumpukan yang memungkinkan Anda untuk:

• Masukkan elemen dengan kompleksitas waktu konstan O (1) dan biaya diamortisasi O (log N) atau O (1) , tergantung pada implementasinya.
• Cari setidaknya untuk waktu konstan - O (1)
• Gabungkan dua Pairing Heap dengan kompleksitas waktu konstan - O (1) dan biaya diamortisasi O (log N) atau O (1) - tergantung pada implementasinya
• Hapus elemen arbitrer (khususnya, minimal) dengan estimasi kompleksitas sementara di O (N) dan estimasi kompleksitas diamortisasi di O (log N)

Secara lebih formal, Pairing Heap adalah pohon arbitrer dengan root khusus yang memenuhi properti heap (kunci dari setiap simpul tidak kurang / tidak lebih dari kunci induknya).
Heap Pairing Heap di mana nilai simpul anak kurang dari nilai simpul orangtua (alias Min Pairing Heap) terlihat seperti ini:



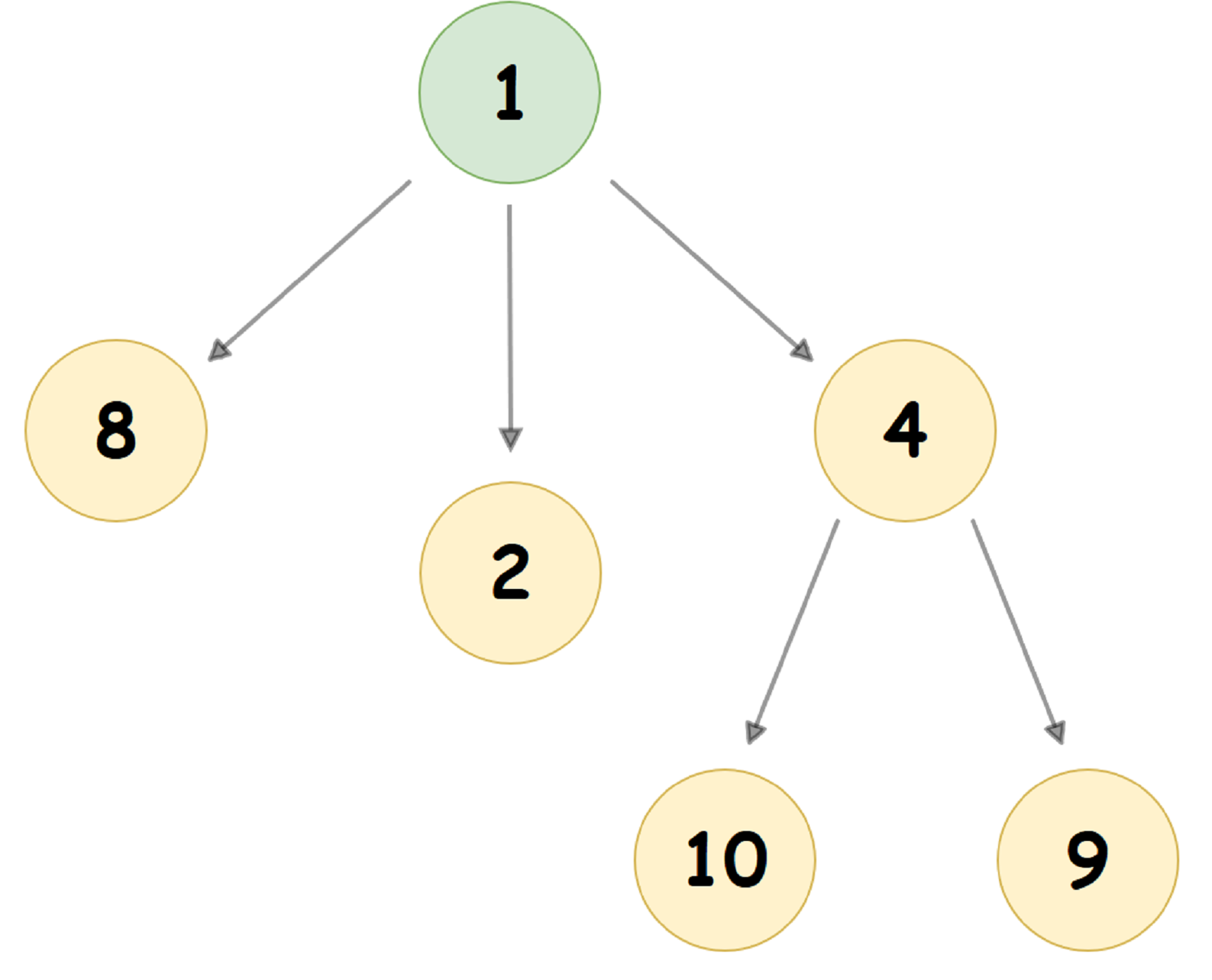
Dalam memori komputer, Pairing-Heap, disajikan sebagai cara yang sangat berbeda: setiap node Tree menyimpan 3 pointer:

• Pointer ke simpul anak paling kiri dari simpul saat ini
• Pointer ke saudara kiri dari simpul
• Pointer ke saudara kanan saudara kandung

Jika salah satu dari simpul yang diindikasikan hilang, penunjuk simpul yang terkait dibatalkan.
Untuk tumpukan yang disajikan pada gambar di atas, kita mendapatkan representasi berikut:



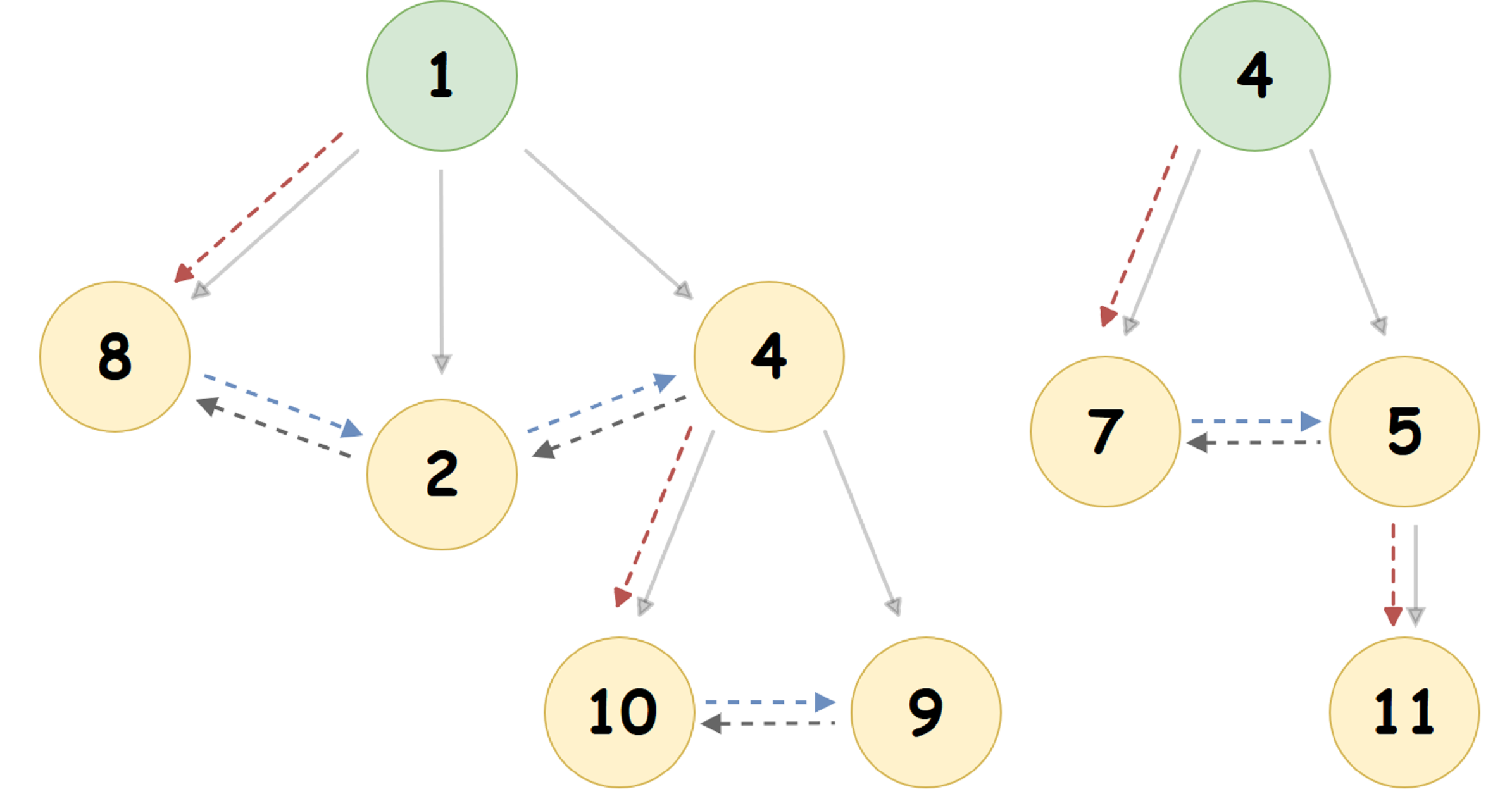Di sini, penunjuk ke simpul anak paling kiri ditunjukkan oleh panah bertitik merah, penunjuk ke saudara simpul yang kanan berwarna biru, dan penunjuk ke saudara kiri berwarna abu-abu. Panah padat menunjukkan representasi Pairing Heap dalam bentuk seperti pohon yang umum untuk seseorang.

Harap perhatikan dua fakta berikut:

• Di akar tumpukan selalu ada saudara kanan dan kiri.
• Jika ada simpul U yang memiliki pointer non-nol ke simpul anak paling kiri, maka simpul ini akan menjadi 'Kepala' dari daftar yang dihubungkan dua kali lipat dari semua simpul anak dari U. Daftar ini disebut siblingList.

Berikutnya, kami mencantumkan algoritma operasi utama di Min Pairing-Heap :

• Masukkan node ke Pairing Heap:
  
  Biarkan di sana diberi Pairing Heap dengan root dan nilai di dalamnya {R, V_1} , serta simpul {U, V_2} . Kemudian, saat memasukkan simpul U ke dalam Pairing Heap yang diberikan:
  
  • Jika kondisi V_2 <V_1 terpenuhi: U menjadi simpul root baru dari heap, 'crowding out' root R ke posisi simpul anak kirinya. Pada saat yang sama, saudara kanan simpul R menjadi simpul paling kiri paling tua, dan penunjuk ke simpul paling kiri dari simpul R menjadi nol.
  • Jika tidak: U menjadi simpul anak paling kiri dari akar R, dan saudara lelakinya yang tertua adalah simpul paling kiri dari akar R.
• Menggabungkan Dua Pasangan Tumpukan:
  
  Biarkan dua Tumpukan Pasangan dengan akar dan nilai di dalamnya {R_1, V_1} , {R_2, V_2}, masing-masing, diberikan. Kami menjelaskan salah satu algoritma untuk menggabungkan tumpukan tersebut ke dalam Pairing Heap yang dihasilkan:
  
  • Pilih tumpukan dengan nilai terendah di root. Biarlah sekelompok {R_1, V_1}.
  • 'Lepaskan' root R_1 dari heap yang dipilih: untuk ini, kita cukup null pointernya ke simpul anak paling kiri.
  • Dengan pointer baru ke simpul anak paling kiri dari root R_1, buat root R_2. Perhatikan bahwa mulai sekarang, R_2 kehilangan status root dan merupakan simpul normal di tumpukan yang dihasilkan.
  • Kami menetapkan saudara yang tepat dari simpul R_2: dengan nilai baru kami membuat penunjuk lama (sebelum penekanan) ke simpul anak paling kiri dari akar R_1, dan untuk R_1, masing-masing, perbarui penunjuk ke saudara kiri.

Pertimbangkan algoritme penggabungan menggunakan contoh spesifik:



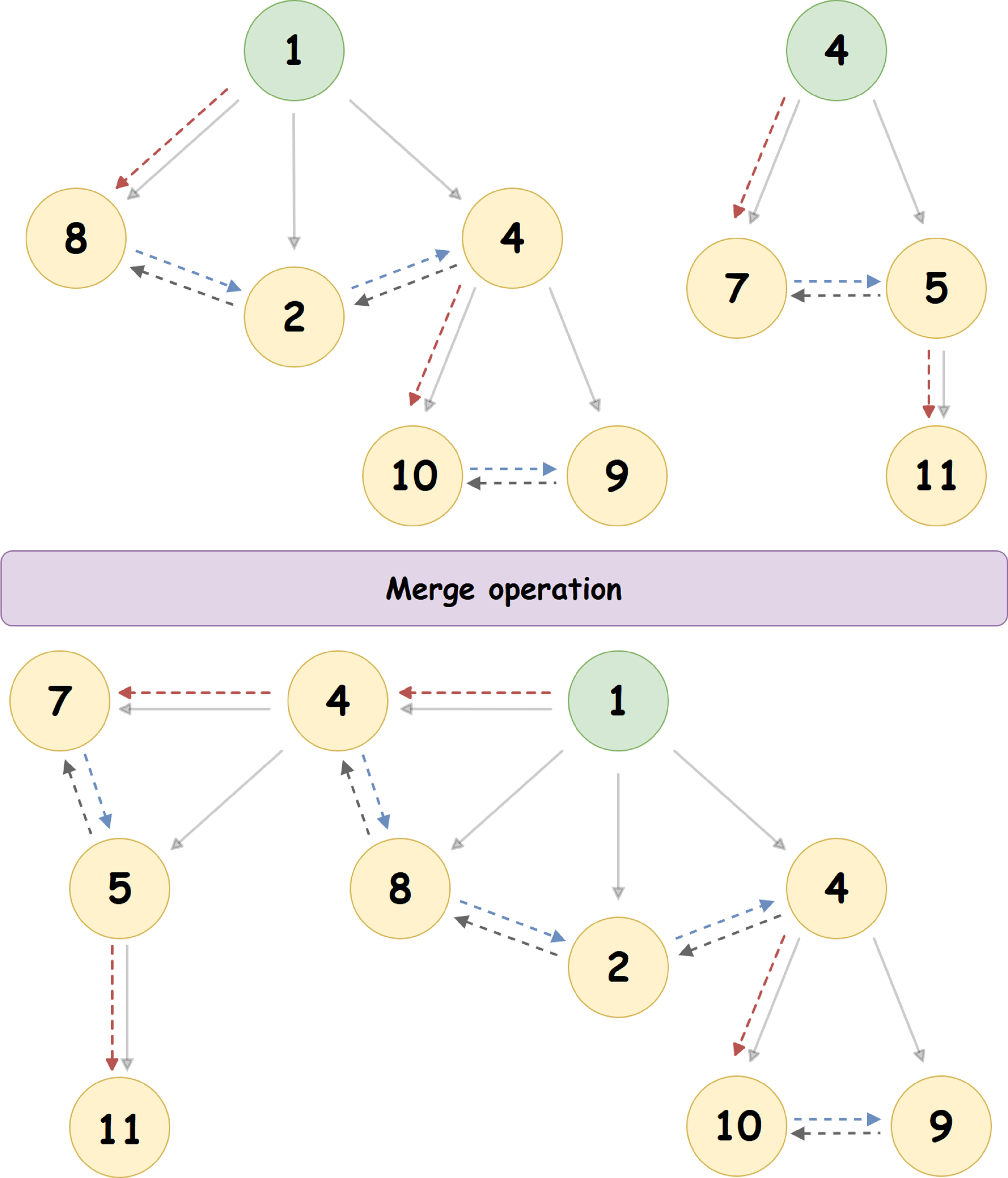Di sini, heap dengan root '4' bergabung dengan heap dengan root '1' (1 <4), menjadi simpul anak paling kiri. Pointer ke saudara kanan simpul '4' - diperbarui, serta pointer ke saudara kiri simpul '8'.

• Menghapus root (simpul dengan nilai minimum) Pairing Heap:
  
  Ada beberapa algoritma untuk menghapus node dari Pairing Heap, dijamin untuk memberikan perkiraan kompleksitas yang diamortisasi dalam O (log N). Kami menggambarkan salah satunya, yang disebut algoritma multipass dan digunakan di JeMalloc:
  
  
  • Kami menghapus root dari heap yang diberikan, hanya menyisakan simpul anak paling kiri.
  • Node anak paling kiri membentuk daftar yang ditautkan ganda dari semua simpul anak dari simpul induk, dan dalam kasus kami, root yang sebelumnya dihapus. Kami akan secara berurutan menelusuri daftar ini sampai akhir dan, dengan mempertimbangkan simpul sebagai akar Pairing Heap yang independen, melakukan operasi penggabungan elemen daftar saat ini dengan yang berikutnya, menempatkan hasilnya dalam antrian FIFO yang telah disiapkan sebelumnya.
  • Sekarang setelah antrian FIFO diinisialisasi, kami akan mengulanginya, melakukan operasi penggabungan elemen antrian saat ini dengan yang berikutnya. Hasil merger ditempatkan di akhir antrian.
  • Kami ulangi langkah sebelumnya sampai satu elemen tetap dalam antrian: Heap Pairing yang dihasilkan.

Contoh proses yang dijelaskan di atas:

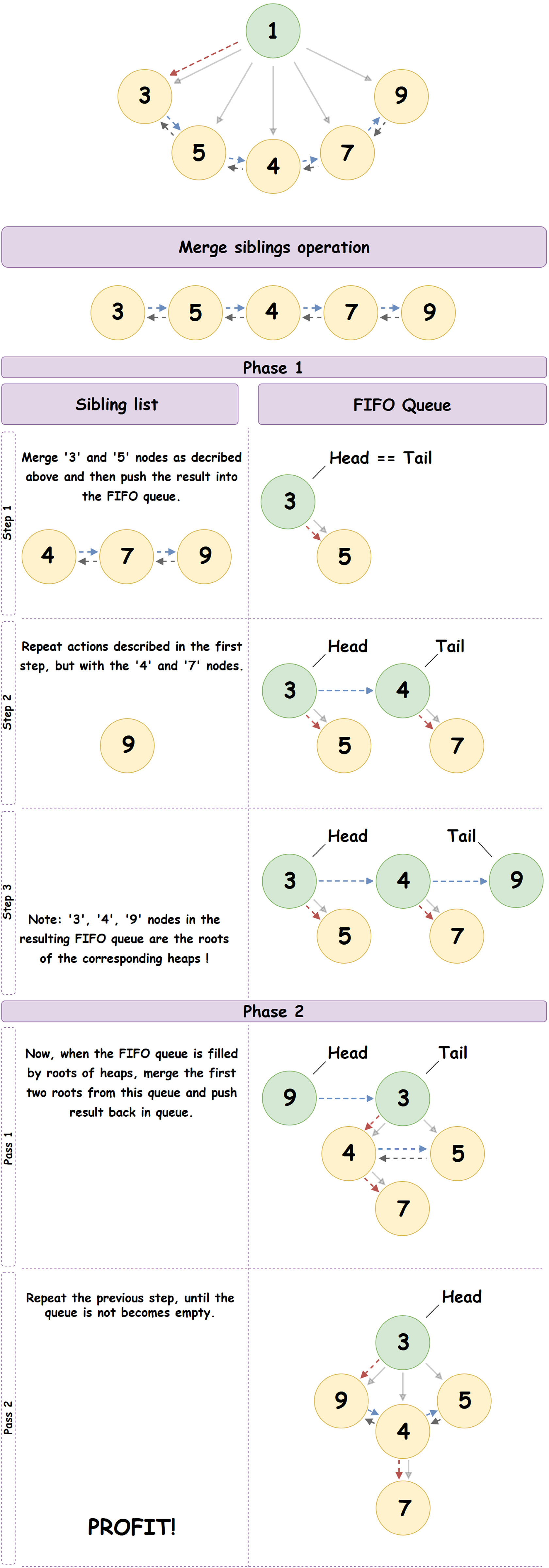
• Menghapus sembarang simpul non-root Pairing Heap:
  
  Pertimbangkan simpul yang dihapus sebagai root dari beberapa subtree dari Heap asli. Pertama, kami menghapus root subtree ini, mengikuti algoritma yang dijelaskan sebelumnya untuk menghapus root Pairing Heap, dan kemudian, melakukan prosedur menggabungkan pohon yang dihasilkan dengan yang asli.
• Mendapatkan elemen Pairing Heap minimum:
  
  Cukup kembalikan nilai root heap.

Namun, kenalan kami dengan Pairing Heap tidak berakhir di sana: Pairing Heap memungkinkan Anda untuk melakukan beberapa operasi tidak segera, tetapi hanya ketika ada kebutuhan untuk itu. Dengan kata lain, Pairing Heap memungkinkan Anda untuk melakukan operasi 'Lazily' , sehingga menurunkan biaya diamortisasi dari beberapa dari mereka.
Misalkan kita membuat insersi K dan menghapus K di Pairing Heap. Jelas, hasil dari operasi ini menjadi perlu hanya ketika kami meminta elemen minimum dari heap.
Mari kita pertimbangkan bagaimana algoritma tindakan dari operasi yang dijelaskan sebelumnya akan berubah selama implementasi Malas mereka:

Mengambil keuntungan dari fakta bahwa root Kuchi memiliki setidaknya dua pointer nol, kita akan menggunakan salah satunya untuk mewakili kepala dari daftar yang ditautkan ganda (selanjutnya disebut auxList ) dari elemen yang dimasukkan ke heap, yang masing-masing akan dianggap sebagai akar Pairing Heap yang independen. Lalu:

• Penyisipan simpul malas di Pairing Heap:
  
  Saat menyisipkan simpul U yang ditentukan ke dalam Pairing Heap { R_1 , V_1 }, kami memasukkannya ke auxList - setelah kepala daftar:

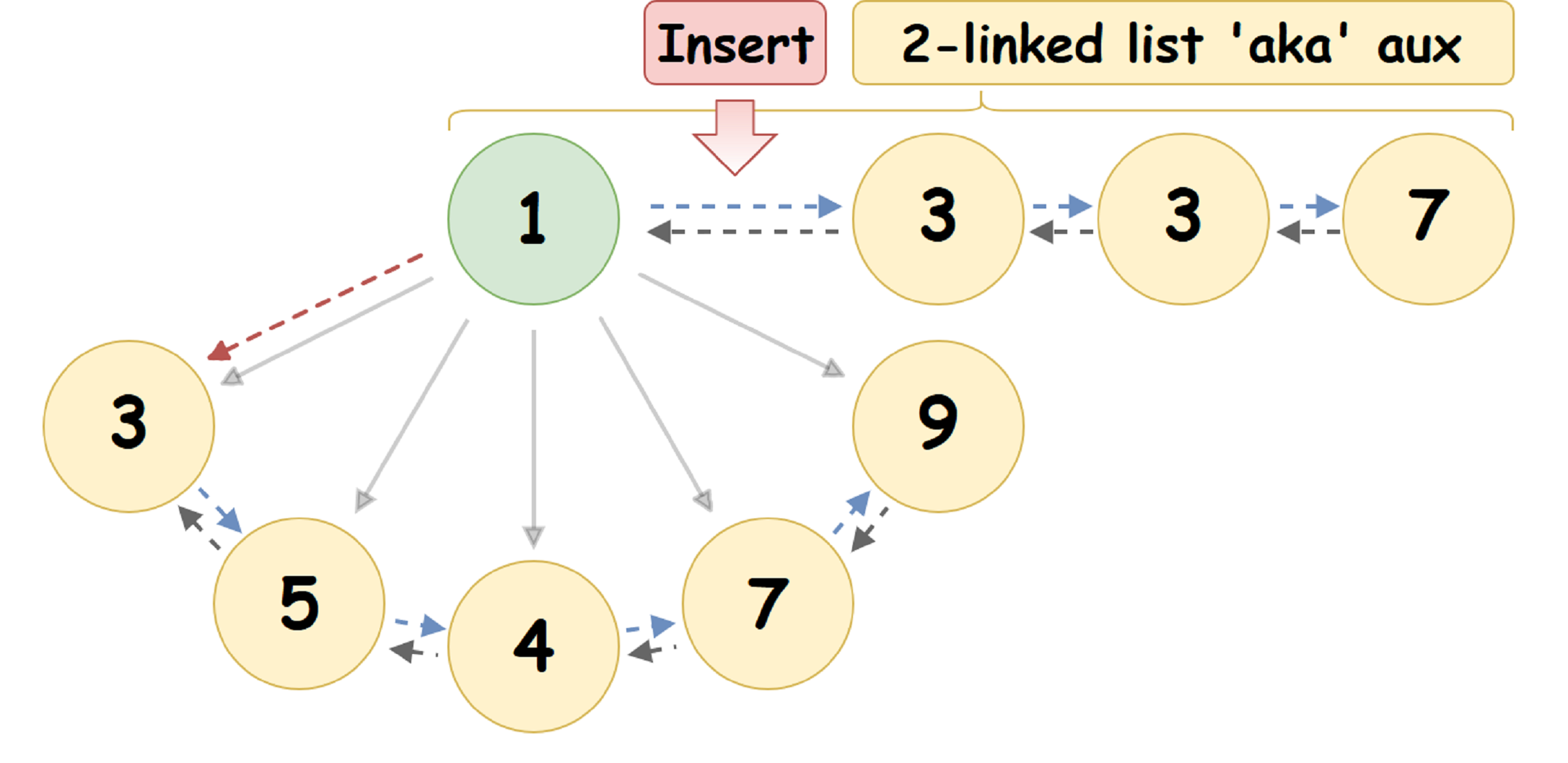
• Penggabungan malas dari Pairing Heap:
  
  Lazy Menggabungkan dua Pairing Heap, mirip dengan penyisipan simpul Lazy, di mana simpul yang dimasukkan adalah root (kepala auxList yang terhubung dua kali lipat) dari salah satu tumpukan.
• Malas mendapatkan elemen Pairing Heap minimum:
  
  Ketika meminta minimum, kita pergi melalui auxList ke daftar akar Pairing Heap independen, berpasangan menggabungkan elemen daftar ini dengan operasi penggabungan, dan mengembalikan nilai root yang mengandung elemen minimum ke salah satu Heather Pairing yang dihasilkan.
• Penghapusan Malas elemen Penumpukan minimum:
  
  Ketika meminta penghapusan elemen minimum yang ditentukan oleh Pairing Heap, pertama-tama kita menemukan node yang mengandung elemen minimum, dan kemudian menghapusnya dari pohon di mana itu adalah root, memasukkan subtree-nya ke dalam auxList heap utama.
• Penghapusan malas dari node Pairing Heap yang sewenang-wenang:
  
  Ketika menghapus node Pairing Heap yang sewenang-wenang, node dihapus dari heap, dan node anaknya dimasukkan ke dalam auxList Heap utama.

Sebenarnya, penggunaan implementasi Lazy Pairing Heap mengurangi biaya pemasangan dan penghapusan node yang sewenang-wenang dalam Pairing Heap: dari O (log N) ke O (1).

Itu saja, dan di bawah ini Anda akan menemukan daftar tautan dan sumber daya yang berguna:

[0] Halaman JeMalloc Github
[1] Artikel asli tentang Pairing Heaps
[2] Artikel asli tentang Laing Implementasi Pairing Heaps
[3] Saluran Telegram tentang optimisasi kode, C ++, Asm, 'level rendah' ​​dan tidak lebih dari itu!

Dilanjutkan ...