Persamaan Navier-Stokes dan simulasi fluida pada CUDA

Hai, Habr. Pada artikel ini, kita akan membahas persamaan Navier-Stokes untuk fluida yang tidak dapat dimampatkan, menyelesaikannya secara numerik, dan membuat simulasi yang indah yang bekerja dengan komputasi paralel pada CUDA. Tujuan utamanya adalah untuk menunjukkan bagaimana Anda dapat menerapkan matematika yang mendasari persamaan dalam praktik saat memecahkan masalah pemodelan cairan dan gas.




Catatan: jika Anda membaca Habr dari perangkat seluler, dan Anda tidak melihat formula, gunakan versi lengkap dari situs

Persamaan Navier-Stokes untuk fluida yang tidak dapat dimampatkan

$$

$${\ partial {\ bf \ vec {u}} \ over {\ partial t}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

Saya pikir setiap orang setidaknya pernah mendengar tentang persamaan ini, beberapa, bahkan mungkin secara analitis menyelesaikan kasus-kasus khusus, tetapi secara umum masalah ini tetap belum terselesaikan sampai sekarang. Tentu saja, kami tidak menetapkan tujuan untuk menyelesaikan masalah milenium dalam artikel ini, namun kami masih dapat menerapkan metode iteratif untuk itu. Tetapi sebagai permulaan, mari kita lihat notasi dalam rumus ini.

Secara konvensional, persamaan Navier-Stokes dapat dibagi menjadi lima bagian:

• $$$\ partial {\ bf \ vec {u}} \ over \ partial t$ - menunjukkan laju perubahan kecepatan fluida pada suatu titik (kami akan mempertimbangkannya untuk setiap partikel dalam simulasi kami).
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - Pergerakan fluida di ruang angkasa.
• $$$- {1 \ lebih dari \ rho} \ nabla {\ bf p}$ Apakah tekanan diberikan pada partikel (di sini $$$\ rho$ - koefisien densitas fluida).
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - viskositas medium (semakin besar itu, semakin kuat cairan menahan gaya yang diterapkan pada bagiannya), $$$\ nu$ - koefisien viskositas).
• $$$\ bf \ vec {F}$ - kekuatan eksternal yang kami terapkan ke fluida (dalam kasus kami, gaya akan memainkan peran yang sangat spesifik - itu akan mencerminkan tindakan yang dilakukan oleh pengguna.

Juga, karena kami akan mempertimbangkan kasus fluida yang tidak dapat dimampatkan dan homogen, kami memiliki persamaan lain: $$${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . Energi di lingkungan itu konstan, tidak ke mana-mana, tidak datang dari mana pun.

Akan salah untuk menghilangkan semua pembaca yang tidak terbiasa dengan analisis vektor , jadi pada saat yang sama dan secara singkat memeriksa semua operator yang ada dalam persamaan (namun, saya sangat menyarankan mengingat apa turunan, diferensial dan vektor, karena mereka mendasari semua itu. apa yang akan dibahas di bawah).

Kita mulai dengan operator nabla, yang merupakan vektor seperti itu (dalam kasus kami, itu akan menjadi dua komponen, karena kami akan memodelkan fluida dalam ruang dua dimensi):

$$

$$\ nabla = {\ begin {pmatrix} {\ partial \ over \ partial x}, {\ partial \ over \ partial y} \ end {pmatrix}}$$

Operator nabla adalah operator diferensial vektor dan dapat diterapkan baik pada fungsi skalar maupun ke vektor. Dalam kasus skalar, kita mendapatkan gradien fungsi (vektor turunan parsialnya), dan dalam kasus vektor, jumlah turunan parsial sepanjang sumbu. Fitur utama dari operator ini adalah bahwa melalui itu Anda dapat mengekspresikan operasi utama analisis vektor - grad ( gradien ), div ( divergence ), rot ( rotor ) dan $$$\ nabla ^ 2$ ( Operator Laplace ). Perlu dicatat segera bahwa ungkapan $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ tidak sama dengan $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - operator nabla tidak memiliki komutatif.

Seperti yang akan kita lihat nanti, ungkapan-ungkapan ini terasa disederhanakan ketika beralih ke ruang diskrit di mana kita akan melakukan semua perhitungan, jadi jangan khawatir jika saat ini Anda tidak begitu jelas tentang apa yang harus dilakukan dengan semua ini. Setelah membagi tugas menjadi beberapa bagian, kami akan menyelesaikannya secara berurutan dan mempresentasikan semua ini dalam bentuk aplikasi berurutan dari beberapa fungsi untuk lingkungan kita.

Solusi numerik dari persamaan Navier-Stokes

Untuk mewakili fluida kita dalam program, kita perlu mendapatkan representasi matematis dari keadaan setiap partikel fluida pada titik waktu yang berubah-ubah. Metode yang paling mudah untuk ini adalah membuat bidang vektor partikel yang menyimpan keadaannya dalam bentuk bidang koordinat:



Di setiap sel array dua dimensi kami, kami akan menyimpan kecepatan partikel pada suatu waktu $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ begin {pmatrix} x, y \ end {pmatrix}$ , dan jarak antara partikel dilambangkan dengan $$$\ delta x$ dan $$$\ delta y$ sesuai. Dalam kode tersebut, cukup bagi kita untuk mengubah nilai kecepatan setiap iterasi, menyelesaikan serangkaian persamaan.

Sekarang kami menyatakan gradien, divergensi, dan operator Laplace dengan mempertimbangkan kordinat kami ( $$$i, j$ - indeks dalam array, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y)}$ - mengambil komponen yang sesuai dari vektor):

Kami selanjutnya dapat menyederhanakan formula diskrit dari operator vektor jika kami menganggap itu $$$\ delta x = \ delta y = 1$ . Asumsi ini tidak akan banyak mempengaruhi keakuratan algoritma, namun, itu mengurangi jumlah operasi per iterasi, dan umumnya membuat ekspresi lebih menyenangkan bagi mata.

Gerakan partikel

Pernyataan ini hanya berfungsi jika kita dapat menemukan partikel terdekat relatif terhadap yang sedang dipertimbangkan saat ini. Untuk meniadakan semua kemungkinan biaya yang terkait dengan menemukannya, kami tidak akan melacak pergerakannya, tetapi dari mana partikel berasal pada awal iterasi dengan memproyeksikan lintasan pergerakan mundur dalam waktu (dengan kata lain, kurangi vektor kecepatan kali perubahan waktu dari posisi saat ini). Dengan menggunakan teknik ini untuk setiap elemen array, kami akan yakin bahwa setiap partikel akan memiliki "tetangga":



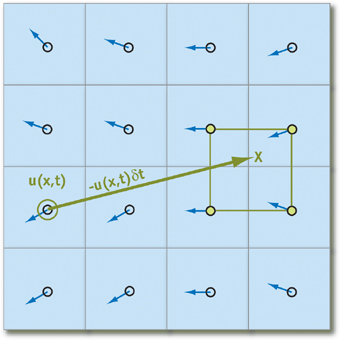
Puting itu $$$q$ - elemen array yang menyimpan status partikel, kami mendapatkan rumus berikut untuk menghitung kondisinya dari waktu ke waktu $$$\ delta t$ (kami percaya bahwa semua parameter yang diperlukan dalam bentuk akselerasi dan tekanan telah dihitung):

$$

$$q ({{\ \ vec {\ bf x}}, t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}, t)$$

Kami segera mencatat bahwa untuk yang cukup kecil $$$\ delta t$ dan kita tidak pernah bisa melampaui batas sel, oleh karena itu sangat penting untuk memilih momentum yang tepat yang akan diberikan pengguna kepada partikel.

Untuk menghindari hilangnya keakuratan dalam hal proyeksi mengenai batas sel atau dalam kasus koordinat non-integer, kami akan melakukan interpolasi bilinear dari keadaan empat partikel terdekat dan menganggapnya sebagai nilai sebenarnya pada titik tersebut. Pada prinsipnya, metode seperti itu praktis tidak akan mengurangi keakuratan simulasi, dan pada saat yang sama itu cukup sederhana untuk diimplementasikan, jadi kami akan menggunakannya.

Viskositas

Setiap cairan memiliki viskositas tertentu, kemampuan untuk mencegah pengaruh kekuatan eksternal pada bagian-bagiannya (madu dan air akan menjadi contoh yang baik, dalam beberapa kasus koefisien viskositasnya berbeda dengan urutan besarnya). Viskositas secara langsung mempengaruhi percepatan yang diperoleh oleh cairan, dan dapat dinyatakan dengan rumus di bawah ini, jika untuk singkatnya kita menghilangkan istilah lain untuk sementara waktu:

$$

$${\ partial \ vec {\ bf u} \ over \ partial t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

. Dalam kasus ini, persamaan iteratif untuk kecepatan mengambil bentuk berikut:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$$

Kami akan sedikit mengubah kesetaraan ini, membawanya ke formulir $$$\ bf A \ vec {x} = \ vec {b}$ (bentuk standar dari sistem persamaan linear):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + \ delta t) = {u ({\ bf \ vec {x}}, t )}$$

dimana $$$\ bf SAYA$ Apakah matriks identitas. Kita perlu transformasi semacam itu untuk kemudian menerapkan metode Jacobi untuk menyelesaikan beberapa sistem persamaan yang serupa. Kami juga akan membahasnya nanti.

Kekuatan eksternal

Langkah paling sederhana dari algoritma adalah penerapan kekuatan eksternal ke medium. Untuk pengguna, ini akan tercermin dalam bentuk klik di layar dengan mouse atau gerakannya. Kekuatan eksternal dapat dijelaskan dengan rumus berikut, yang kami terapkan untuk setiap elemen matriks ( $$$\ vec {\ bf G}$ - vektor momentum $$$x_p, y_p$ - posisi mouse $$$x, y$ - Koordinat sel saat ini, $$$r$ - radius aksi, parameter penskalaan):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ kiri (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ over r} \ benar)$$

Vektor impuls dapat dengan mudah dihitung sebagai perbedaan antara posisi mouse sebelumnya dan yang sekarang (jika ada), dan di sini Anda masih bisa berkreasi. Di bagian algoritme inilah kita bisa memperkenalkan penambahan warna pada cairan, iluminasi, dll. Kekuatan eksternal juga dapat mencakup gravitasi dan suhu, dan meskipun tidak sulit untuk menerapkan parameter tersebut, kami tidak akan mempertimbangkannya dalam artikel ini.

Tekanan

Tekanan dalam persamaan Navier-Stokes adalah gaya yang mencegah partikel mengisi semua ruang yang tersedia bagi mereka setelah menerapkan gaya eksternal apa pun kepada mereka. Segera, perhitungannya sangat sulit, tetapi masalah kita dapat sangat disederhanakan dengan menerapkan teorema dekomposisi Helmholtz .

Panggil $$$\ bf \ vec {W}$ bidang vektor diperoleh setelah menghitung perpindahan, kekuatan eksternal dan viskositas. Ini akan memiliki divergensi bukan-nol, yang bertentangan dengan kondisi ketidakmampatan cairan ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ), dan untuk memperbaikinya, perlu untuk menghitung tekanan. Menurut teorema dekomposisi Helmholtz, $$$\ bf \ vec {W}$ dapat direpresentasikan sebagai jumlah dari dua bidang:

$$

$$\ bf \ vec {W} = \ vec {u} + \ nabla p$$

dimana $$$\ bf u$ - ini adalah bidang vektor yang kita cari dengan nol divergensi. Tidak ada bukti kesetaraan ini akan diberikan dalam artikel ini, tetapi pada akhirnya Anda dapat menemukan tautan dengan penjelasan terperinci. Kita dapat menerapkan operator nabla di kedua sisi ekspresi untuk mendapatkan rumus berikut untuk menghitung bidang tekanan skalar:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$$

Ungkapan yang ditulis di atas adalah persamaan Poisson untuk tekanan. Kita juga bisa menyelesaikannya dengan metode Jacobi yang disebutkan di atas, dan dengan demikian menemukan variabel terakhir yang tidak diketahui dalam persamaan Navier-Stokes. Pada prinsipnya, sistem persamaan linear dapat diselesaikan dalam berbagai cara yang berbeda dan canggih, tetapi kita masih akan memikirkan yang paling sederhana dari mereka, agar tidak semakin membebani artikel ini.

Batas dan kondisi awal

Setiap persamaan diferensial yang dimodelkan pada domain terbatas memerlukan kondisi awal atau batas yang ditentukan dengan benar, jika tidak, kita sangat mungkin mendapatkan hasil yang secara fisik salah. Kondisi batas ditetapkan untuk mengontrol perilaku fluida di dekat tepi kisi koordinat, dan kondisi awal menentukan parameter yang dimiliki partikel pada saat program dimulai.

Kondisi awal akan sangat sederhana - awalnya fluida stasioner (kecepatan partikel nol), dan tekanannya juga nol. Kondisi batas akan ditetapkan untuk kecepatan dan tekanan oleh rumus yang diberikan:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ lebih dari 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ lebih dari 2 \ delta x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ over \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ over \ delta y} = 0$$

Dengan demikian, kecepatan partikel di tepi akan berlawanan dengan kecepatan di tepi (dengan demikian mereka akan mengusir dari tepi), dan tekanannya sama dengan nilai tepat di sebelah batas. Operasi ini harus diterapkan ke semua elemen pembatas dari array (misalnya, ada ukuran kisi $$$N \ kali M$ , lalu kami menerapkan algoritme untuk sel yang ditandai dengan warna biru pada gambar):

Pewarna

Dengan apa yang kita miliki sekarang, Anda sudah dapat menemukan banyak hal menarik. Misalnya, sadari penyebaran pewarna dalam cairan. Untuk melakukan ini, kita hanya perlu memelihara bidang skalar lain, yang akan bertanggung jawab untuk jumlah cat pada setiap titik simulasi. Formula untuk memperbarui pewarna sangat mirip dengan kecepatan, dan dinyatakan sebagai:

$$

$${\ partial d \ over \ partial t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$$

Dalam formula $$$S$ bertanggung jawab untuk mengisi kembali area tersebut dengan pewarna (mungkin tergantung di mana pengguna mengklik), $$$d$ langsung adalah jumlah pewarna pada titik tersebut, dan $$$\ gamma$ - koefisien difusi. Memecahkannya tidak sulit, karena semua pekerjaan dasar tentang derivasi formula telah dilakukan, dan cukup untuk membuat beberapa pergantian. Cat dapat diimplementasikan dalam kode sebagai warna dalam format RGB, dan dalam hal ini tugas dikurangi menjadi operasi dengan beberapa nilai nyata.

Vortisitas

Persamaan vortisitas bukan bagian langsung dari persamaan Navier-Stokes, tetapi merupakan parameter penting untuk simulasi yang masuk akal dari gerakan pewarna dalam cairan. Karena fakta bahwa kami memproduksi algoritme pada bidang diskrit, serta karena kerugian dalam akurasi nilai floating-point, efek ini hilang, dan oleh karena itu kami perlu mengembalikannya dengan menerapkan gaya tambahan ke setiap titik dalam ruang. Vektor gaya ini ditetapkan sebagai $$$\ bf \ vec {T}$ dan ditentukan oleh rumus berikut:

$$

$$\ bf \ omega = \ nabla \ times \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$$

$$$\ omega$ ada hasil penerapan rotor ke vektor kecepatan (definisinya diberikan di awal artikel), $$$\ vec \ eta$ - gradien bidang skalar dari nilai absolut $$$\ omega$ . $$$\ vec \ psi$ mewakili vektor yang dinormalisasi $$$\ vec \ eta$ , dan $$$\ epsilon$ Merupakan konstanta yang mengontrol seberapa besar vortisitas dalam cairan kita nantinya.

Metode Jacobi untuk memecahkan sistem persamaan linear

Dalam menganalisis persamaan Navier-Stokes, kami menemukan dua sistem persamaan - satu untuk viskositas dan yang lainnya untuk tekanan. Mereka dapat diselesaikan dengan algoritma iteratif, yang dapat dijelaskan dengan rumus iteratif berikut:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ alpha b_ {i, j}} \ lebih dari \ beta}$$

Untuk kita $$$x$ - elemen array yang mewakili bidang skalar atau vektor. $$$k$ - nomor iterasi, kita dapat menyesuaikannya untuk meningkatkan akurasi perhitungan atau sebaliknya untuk menguranginya dan meningkatkan produktivitas.

Untuk menghitung viskositas, kami mengganti: $$$x = b = \ bf \ vec {u}$ , $$$\ alpha = {1 \ over \ nu \ delta t}$ , $$$\ beta = 4+ \ alpha$ , di sini adalah parameternya $$$\ beta$ - jumlah bobot. Jadi, kita perlu menyimpan setidaknya dua bidang kecepatan vektor untuk membaca nilai-nilai satu bidang secara independen dan menulisnya ke bidang lain. Rata-rata, untuk menghitung bidang kecepatan dengan metode Jacobi, perlu dilakukan 20-50 iterasi, yang cukup banyak jika kita melakukan perhitungan pada CPU.

Untuk persamaan tekanan, kami membuat substitusi berikut: $$$x = p$ , $$$b = \ nabla \ bf \ cdot \ vec {W}$ , $$$\ alpha = -1$ , $$$\ beta = 4$ . Hasilnya, kami mendapat nilai $$$p_ {i, j} \ delta t$ pada intinya. Tetapi karena ini hanya digunakan untuk menghitung gradien yang dikurangi dari bidang kecepatan, transformasi tambahan dapat dihilangkan. Untuk bidang tekanan, yang terbaik adalah melakukan iterasi 40-80, karena dengan jumlah yang lebih kecil perbedaannya menjadi terlihat.

Implementasi algoritma

Kami akan mengimplementasikan algoritme di C ++, kami juga membutuhkan Cuda Toolkit (Anda dapat membaca cara menginstalnya di situs web Nvidia), serta SFML . Kami membutuhkan CUDA untuk memparalelkan algoritme, dan SFML hanya akan digunakan untuk membuat jendela dan menampilkan gambar di layar (Pada prinsipnya, ini dapat ditulis dalam OpenGL, tetapi perbedaan dalam kinerjanya tidak signifikan, tetapi kode akan bertambah 200 baris lainnya).

Toolkit Cuda

Pertama, kita akan berbicara sedikit tentang cara menggunakan Cuda Toolkit untuk memparalelkan tugas. Panduan yang lebih rinci disediakan oleh Nvidia sendiri, jadi di sini kami membatasi diri hanya untuk yang paling diperlukan. Diasumsikan bahwa Anda dapat menginstal kompilator, dan Anda dapat membangun proyek pengujian tanpa kesalahan.

Untuk membuat fungsi yang berjalan pada GPU, pertama-tama Anda harus mendeklarasikan berapa banyak kernel yang ingin kita gunakan, dan berapa blok kernel yang perlu kita alokasikan. Untuk ini, Cuda Toolkit memberi kita struktur khusus - dim3 , dengan menetapkan semua nilai x, y, z secara default ke 1. Dengan menetapkannya sebagai argumen saat memanggil fungsi, kita dapat mengontrol jumlah kernel yang dialokasikan. Karena kita bekerja dengan array dua dimensi, kita hanya perlu mengatur dua bidang dalam konstruktor: x dan y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

di mana size_x dan size_y adalah ukuran array yang sedang diproses. Tanda tangan dan panggilan fungsi adalah sebagai berikut (tanda kurung tiga sudut diproses oleh kompiler Cuda):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

Dalam fungsi itu sendiri, Anda dapat mengembalikan indeks array dua dimensi melalui nomor blok dan nomor kernel di blok ini menggunakan rumus berikut:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

Perlu dicatat bahwa fungsi yang dieksekusi pada kartu video harus ditandai dengan tag __global__ , dan juga mengembalikan batal , sehingga paling sering hasil perhitungan ditulis ke array yang dilewatkan sebagai argumen dan pra-dialokasikan dalam memori kartu video.

Fungsi CudaMalloc dan CudaFree bertanggung jawab untuk membebaskan dan mengalokasikan memori pada kartu video. Kami dapat beroperasi pada pointer ke area memori yang mereka kembalikan, tetapi kami tidak dapat mengakses data dari kode utama. Cara termudah untuk mengembalikan hasil perhitungan adalah dengan menggunakan cudaMemcpy , mirip dengan memcpy standar, tetapi dapat menyalin data dari kartu video ke memori utama dan sebaliknya.

SFML dan render jendela

Berbekal semua pengetahuan ini, kita akhirnya bisa beralih ke menulis kode secara langsung. Untuk memulai, mari buat file main.cpp dan letakkan semua kode tambahan untuk render jendela di sana:


baris di awal fungsi utama

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

menciptakan gambar RGBA dalam bentuk array satu dimensi dengan panjang konstan. Kami akan meneruskannya bersama dengan parameter lain (posisi mouse, perbedaan antara frame) ke fungsi computeField . Yang terakhir, serta beberapa fungsi lainnya, dideklarasikan di kernel.cu dan memanggil kode yang dieksekusi pada GPU. Anda dapat menemukan dokumentasi tentang salah satu fungsi di situs web SFML, tidak ada yang super menarik terjadi dalam kode file, jadi kami tidak akan berhenti di situ lama.

Komputasi GPU

Untuk mulai menulis kode di bawah GPU, pertama buat file kernel.cu dan tentukan beberapa kelas tambahan di dalamnya: Color3f, Vec2, Config, SystemConfig :


Atribut __host__ di depan nama metode berarti bahwa kode dapat dieksekusi pada CPU, __device__ , sebaliknya, mewajibkan kompiler untuk mengumpulkan kode di bawah GPU. Kode menyatakan primitif untuk bekerja dengan vektor dua komponen, warna, konfigurasi dengan parameter yang dapat diubah dalam runtime, serta beberapa pointer statis ke array, yang akan kita gunakan sebagai buffer untuk perhitungan.

cudaInit dan cudaExit juga didefinisikan dengan sangat sepele:


Dalam fungsi inisialisasi, kami mengalokasikan memori untuk array dua dimensi, menentukan array warna yang akan kami gunakan untuk mengecat cairan, dan juga menetapkan nilai default dalam konfigurasi. Di cudaExit, kami hanya membebaskan semua buffer. Kedengarannya paradoks, untuk menyimpan array dua dimensi, paling menguntungkan untuk menggunakan array satu dimensi, akses yang akan dilakukan dengan ekspresi berikut:

 array[y * size_x + x]; // equals to array[y][x] 

Kami memulai implementasi algoritma langsung dengan fungsi pergerakan partikel. Bidang oldField dan newField (bidang tempat data berasal dan dari mana mereka dituliskan), ukuran array, serta waktu delta dan koefisien densitas (digunakan untuk mempercepat pembubaran pewarna dalam cairan dan membuat media tidak terlalu sensitif untuk memajukan, ditransfer untuk maju tindakan pengguna). Fungsi interpolasi bilinear diimplementasikan dengan cara klasik melalui perhitungan nilai-nilai antara:


Diputuskan untuk membagi fungsi difusi viskositas menjadi beberapa bagian: computeDiffusion dipanggil dari kode utama, yang memanggil diffuse dan computeColor beberapa kali yang telah ditentukan, dan kemudian menukar array dari tempat kami mengambil data dan yang mana kami menulisnya. Ini adalah cara termudah untuk mengimplementasikan pemrosesan data paralel, tetapi kami menghabiskan memori dua kali lebih banyak.

Kedua fungsi menyebabkan variasi metode Jacobi. Tubuh jacobiColor dan jacobiVelocity segera memeriksa bahwa elemen saat ini tidak di perbatasan - dalam hal ini, kita harus mengaturnya sesuai dengan rumus yang dijelaskan di bagian Batas dan kondisi awal .


Penggunaan kekuatan eksternal diimplementasikan melalui fungsi tunggal - applyForce , yang mengambil sebagai argumen posisi mouse, warna pewarna, serta radius aksi. Dengan bantuannya, kita dapat memberi kecepatan pada partikel-partikel tersebut, serta mengecatnya. Eksponen persaudaraan memungkinkan Anda untuk membuat area tidak terlalu tajam, dan pada saat yang sama cukup jelas dalam radius yang ditentukan.


Perhitungan vortisitas sudah merupakan proses yang lebih rumit, oleh karena itu kami mengimplementasikannya dalam computeVorticity dan applyVorticity , kami juga mencatat bahwa bagi mereka perlu mendefinisikan dua operator vektor seperti curl (rotor) dan absGradient (gradien dari nilai medan absolut). Untuk menentukan efek vortex tambahan, kami mengalikan $$$y$ komponen vektor gradien aktif $$$-1$ , dan kemudian menormalkannya dengan membaginya dengan panjang (tanpa lupa untuk memeriksa bahwa vektor itu bukan nol):


Langkah selanjutnya dalam algoritma akan menjadi perhitungan medan tekanan skalar dan proyeksi pada bidang kecepatan. Untuk melakukan ini, kita perlu mengimplementasikan 4 fungsi: divergensi , yang akan mempertimbangkan divergensi kecepatan, jacobiPressure , yang mengimplementasikan metode Jacobi untuk tekanan, dan computePressure dengan computePressureImpl , yang mengulangi perhitungan lapangan:


Proyeksi ini cocok dalam dua fungsi kecil - proyek dan gradien yang membutuhkan tekanan. Ini bisa dikatakan tahap terakhir dari algoritma simulasi kami:


Setelah proyeksi, kita dapat dengan aman melanjutkan render gambar ke buffer dan berbagai efek pasca. Fungsi cat menyalin warna dari bidang partikel ke array RGBA. Fungsi applyBloom juga diterapkan, yang menyoroti cairan ketika kursor diletakkan di atasnya dan tombol mouse ditekan. Dari pengalaman, teknik ini membuat gambar lebih menyenangkan dan menarik bagi mata pengguna, tetapi tidak perlu sama sekali.

Dalam post-processing, Anda juga dapat menyorot tempat-tempat di mana fluida memiliki kecepatan tertinggi, mengubah warna tergantung pada vektor gerakan, menambahkan berbagai efek, dll., Tetapi dalam kasus kami, kami akan membatasi diri pada jenis minimum, karena bahkan dengan itu gambarnya sangat menarik (terutama dalam dinamika) :


Dan pada akhirnya, kita masih memiliki satu fungsi utama yang kita panggil dari main.cpp - computeField . Ini menghubungkan semua potongan algoritma, memanggil kode pada kartu video, dan juga menyalin data dari gpu ke cpu. Ini juga berisi perhitungan vektor momentum dan pilihan warna pewarna, yang kami sampaikan untuk menerapkan Force :

Kesimpulan

Pada artikel ini, kami menganalisis algoritma numerik untuk menyelesaikan persamaan Navier-Stokes dan menulis sebuah program simulasi kecil untuk fluida yang tidak dapat dimampatkan. Mungkin kami tidak memahami semua seluk-beluknya, tetapi saya berharap bahwa materi tersebut ternyata menarik dan bermanfaat bagi Anda, dan setidaknya berfungsi sebagai pengantar yang baik untuk bidang pemodelan cairan.

Sebagai penulis artikel ini, saya akan dengan tulus menghargai komentar dan tambahan, dan akan mencoba menjawab semua pertanyaan Anda di bawah posting ini.

Materi tambahan

Anda dapat menemukan semua kode sumber dalam artikel ini di repositori Github saya. Setiap saran untuk perbaikan dipersilahkan.

Bahan asli yang dijadikan dasar untuk artikel ini dapat ditemukan di situs web resmi Nvidia. Ini juga menyajikan contoh-contoh implementasi bagian-bagian algoritma dalam bahasa shader:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

Bukti teorema dekomposisi Helmholtz dan sejumlah besar bahan tambahan tentang mekanika fluida dapat ditemukan dalam buku ini (Bahasa Inggris, lihat bagian 1.2):
Chorin, AJ, dan JE Marsden. 1993. Pengantar Matematika untuk Mekanika Fluida. Edisi ke-3. Springer

Saluran satu YouTube berbahasa Inggris, membuat konten berkualitas yang berkaitan dengan matematika, dan menyelesaikan persamaan diferensial khususnya (Bahasa Inggris). Video yang sangat visual yang membantu memahami esensi banyak hal dalam matematika dan fisika:
3Blue1Brown -
Persamaan Diferensial YouTube (3Blue1Brown)

Saya juga berterima kasih kepada WhiteBlackGoose atas bantuannya dalam menyiapkan materi untuk artikel.

---

Dan pada akhirnya, bonus kecil - beberapa tangkapan layar yang indah diambil dalam program:


Streaming langsung (pengaturan default)


Whirlpool (radius besar dalam berlaku Force)


Gelombang (vortisitas tinggi + difusi)

Juga, dengan permintaan populer, saya menambahkan video dengan simulasi: