Hai, habrozhiteli! Kami baru-baru ini menyerahkan
buku Quantum Computing for Real IT kepada Chris Bernhard. Di sini mereka memutuskan untuk membagikan kutipan dari buku "Algoritma dan Pencarian Data Grover"
Kami memasuki era big data. Mencari dataset raksasa secara efisien saat ini menjadi perhatian besar bagi banyak perusahaan besar. Algoritma Grover secara teoritis mampu mempercepat pengambilan data.
Love Grover menemukan algoritma-nya pada tahun 1996. Seperti algoritma Deutsch dan Simon, ia memiliki kecepatan eksekusi yang lebih tinggi dibandingkan dengan algoritma klasik dalam hal kompleksitas kueri. Namun, kami tidak akan dapat mengimplementasikan algoritma pencarian data saat ini tanpa nubuat yang dapat mengajukan pertanyaan mereka. Kita harus membangun sebuah algoritma yang melakukan pekerjaan oracle. Tetapi sebelum kita mulai berbicara tentang implementasi algoritma Grover, mari kita lihat apa yang dilakukannya dan bagaimana caranya.
Algoritma Grover
Bayangkan Anda memiliki empat kartu remi. Mereka terbalik. Anda tahu bahwa salah satunya adalah as cacing dan Anda harus menemukannya. Berapa banyak kartu yang harus Anda balikkan sampai Anda tahu di mana letak cacing?
Jika Anda beruntung, Anda akan menemukan kartu yang diinginkan pada percobaan pertama, jika Anda tidak beruntung, Anda dapat membalik tiga kartu, dan tidak satu pun dari mereka akan menjadi kartu as cacing. Dalam kasus terburuk, membalik tiga kartu, Anda akan tahu pasti bahwa kartu terakhir adalah kartu as yang Anda cari. Jadi, kita bisa mencari tahu di mana ace berada dengan membalik dari satu ke tiga kartu. Rata-rata, Anda perlu membalik 2,25 kartu.
Ini adalah salah satu tugas yang diselesaikan algoritma Grover. Sebelum memulai deskripsi algoritma, kami merumuskan kembali masalah. Kami memiliki empat sekuens biner: 00, 01, 10 dan 11. Kami memiliki fungsi f yang mengembalikan 0 untuk tiga sekuens ini dan 1 untuk sekuens keempat. Kita perlu menemukan urutan biner yang sesuai dengan nilai output 1. Misalnya, kita bisa mendapatkan hasil berikut: f (00) = 0, f (01) = 0, f (10) = 1 dan f (11) = 0. Sekarang masalahnya adalah adalah untuk mengetahui berapa kali fungsi harus dihitung untuk mendapatkan hasil f (10) = 1. Di sini kita hanya merumuskan kembali masalah dengan mengganti kartu bermain dengan fungsi, sehingga jawaban untuk pertanyaan ini sudah diketahui: seperti sebelumnya, rata-rata akan diperlukan untuk menghitung fungsi 2,25 kali.
Seperti semua algoritme kueri kompleksitas, kami membuat oracle - gerbang yang merangkum suatu fungsi. Oracle untuk contoh kita, di mana hanya ada empat urutan biner, ditunjukkan pada Gambar. 9.1.
Rantai untuk algoritma Grover ditunjukkan pada Gambar. 9.2.
Algoritma melakukan dua langkah. Pada yang pertama, tanda amplitudo probabilitas dibalik, terkait dengan tempat yang kami coba temukan. Yang kedua memperkuat amplitudo probabilitas ini. Mari kita lihat bagaimana rantai melakukan ini.
Setelah transmisi melalui katup Hadamard, dua qubit atas mendapatkan status
dan qubit yang lebih rendah memiliki status
Negara gabungan dapat ditulis sebagai
Qubit kemudian melewati gerbang F. Ini membalikkan 0 dan 1 di qubit ketiga ke lokasi yang kami coba temukan. Untuk kasus kami f (10) = 1 kami dapatkan
Ini dapat ditulis ulang sebagai
Hasilnya, kita mendapatkan dua qubit atas, tidak bingung dengan yang lebih rendah, tetapi amplitudo probabilitas
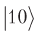
akan mengubah tanda, menunjukkan lokasi yang diinginkan.
Jika kita mengukur dua qubit atas pada langkah ini, kita mendapatkan satu dari empat lokasi, dan keempat kemungkinan jawaban sama-sama memungkinkan. Kita perlu mengambil langkah lain - untuk meningkatkan amplitudo probabilitas. Amplifikasi dilakukan dengan membalik urutan angka relatif terhadap rata-rata mereka. Jika angkanya di atas rata-rata, ia membalik dan menjadi di bawah rata-rata. Jika jumlahnya di bawah rata-rata, itu membalik dan menjadi di atas rata-rata. Dalam setiap kasus, keterpencilan dari rata-rata dipertahankan. Sebagai ilustrasi, kami menggunakan empat angka: 1, 1, 1, dan –1. Jumlah mereka 2, dan rata-rata 2/4, atau 1/2. Kemudian kita mulai memilah-milah angka dalam urutan. Angka pertama adalah 1. Angka ini 1/2 di atas rata-rata. Setelah kudeta, itu seharusnya 1/2 lebih rendah dari rata-rata. Dalam hal ini, itu akan berubah menjadi 0. Angka –1 berada di bawah rata-rata 3/2. Setelah kudeta, itu harus menjadi 3/2 di atas rata-rata, yaitu berubah menjadi 2.
Dua qubit atas saat ini memiliki status
Mengubah amplitudo relatif terhadap rata-rata, kami dapatkan

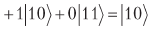
.
Setelah menyelesaikan pengukuran, kita pasti akan mendapatkan 10, yaitu, revolusi relatif terhadap rata-rata memberi kita apa yang kita butuhkan. Yang harus kita lakukan adalah memastikan ada gerbang atau, apa pula, matriks ortogonal yang menggambarkan revolusi relatif terhadap rata-rata. Matriks seperti itu ada:
Sebagai hasil dari aksi katup pada dua qubit atas, kita dapatkan
Dalam contoh ini, di mana kita hanya memiliki dua qubit, kita harus menggunakan oracle hanya sekali. Cukuplah bagi kita untuk mengajukan satu-satunya pertanyaan. Untuk kasus n = 2, algoritma Grover memberikan jawaban yang tepat setelah satu pertanyaan, sedangkan dalam kasus klasik, rata-rata, 2,25 pertanyaan perlu ditanyakan.
Gagasan ini meluas ke kasus jumlah n qubit yang sewenang-wenang. Kita mulai dengan memutar tanda amplitudo probabilitas, yang sesuai dengan lokasi yang diinginkan. Kemudian kami melakukan revolusi relatif terhadap rata-rata. Namun, dalam kasus ini, amplifikasi amplitudo tidak terjadi secara signifikan seperti pada situasi dengan dua qubit. Ambil contoh delapan angka, tujuh di antaranya adalah 1 dan satu adalah -1. Jumlah mereka 6, dan rata-rata 6/8. Setelah flip, rata-rata 1 akan berubah 1/2, dan –1 akan berubah 10/4. Akibatnya, di hadapan tiga qubit, mengukur satu qubit setelah amplifikasi amplitudo, kami akan mendapatkan lokasi yang diinginkan dengan probabilitas lebih tinggi daripada yang lain. Masalahnya adalah bahwa ada peluang yang signifikan untuk mendapatkan jawaban yang salah. Kami membutuhkan probabilitas yang lebih tinggi untuk mendapatkan jawaban yang benar - kami perlu memperbesar amplitude sebelum mengukur. Solusinya adalah mentransfer semua qubit kembali melalui rantai. Kami kembali membalik tanda amplitudo probabilitas yang terkait dengan lokasi yang diinginkan dan membalik lagi relatif terhadap rata-rata.
Pertimbangkan kasus umum. Kita perlu menemukan sesuatu di salah satu lokasi yang mungkin. Untuk menemukannya dengan cara klasik, dalam kasus terburuk kita harus mengajukan pertanyaan m - 1. Jumlah pertanyaan tumbuh sebanding dengan m. Grover menghitung formula yang menentukan berapa kali rantai perlu digunakan untuk mendapatkan probabilitas maksimum dari jawaban yang benar. Angka yang diberikan formula ini tumbuh secara proporsional
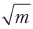
. Ini adalah akselerasi kuadratik.
Aplikasi Algoritma Grover
Ada beberapa masalah dengan implementasi algoritma. Pertama, akselerasi kuadratik dievaluasi relatif terhadap permintaan kompleksitas. Untuk menggunakan oracle, Anda harus membuatnya, dan jika Anda tidak melakukan tugas ini dengan hati-hati, jumlah langkah yang dilakukan oleh oracle akan melebihi jumlah langkah yang disimpan algoritma, dan sebagai hasilnya, algoritma akan menjadi lebih lambat daripada lebih cepat daripada yang klasik. Masalah lain adalah bahwa, dengan menentukan akselerasi, kita mengasumsikan bahwa kumpulan data tidak teratur. Jika kumpulan data memiliki struktur tertentu, Anda sering dapat menemukan algoritma klasik yang menggunakan struktur ini dan mencari solusi lebih cepat. Masalah terakhir terkait dengan akselerasi. Akselerasi kuadrat tidak lebih dari akselerasi eksponensial, yang kami amati dalam algoritma lain. Apakah mungkin meraih lebih banyak? Mari kita lihat masalah ini.
Kedua masalah yang terkait dengan implementasi oracle dan keberadaan struktur dalam set data dibenarkan dan menunjukkan bahwa dalam kebanyakan kasus algoritma Grover tidak memiliki aplikasi praktis untuk mencari database. Tetapi dalam beberapa situasi, memiliki struktur dalam data memungkinkan untuk membuat oracle yang bertindak dengan efisiensi tinggi. Dalam situasi seperti itu, algoritma dapat menyalip algoritma klasik. Jawaban atas pertanyaan tentang kemungkinan mencapai kesuksesan yang lebih besar telah diberikan. Terbukti bahwa algoritma Grover optimal. Tidak ada algoritma kuantum yang mampu memecahkan masalah dengan lebih dari percepatan kuadratik. Akselerasi kuadratik, meskipun tidak mengesankan seperti eksponensial, masih memberikan beberapa manfaat. Saat bekerja dengan kumpulan data besar, percepatan apa pun bisa berharga.
Kemungkinan algoritma Grover akan menemukan aplikasi utama bukan untuk pencarian, seperti yang disajikan di atas, tetapi untuk variasinya. Secara khusus, gagasan memperkuat amplitudo mungkin berguna.
Kami memeriksa hanya beberapa algoritma, tetapi algoritma Shore dan Grover dianggap yang paling penting. Ada banyak algoritma lain yang didasarkan pada ide-ide yang melekat dalam dua ini. Sekarang mari kita mengalihkan perhatian kita dari algoritma kuantum ke bidang lain penerapan komputasi kuantum.