Halo semuanya! Nama saya Dmitry Rudnev, saya adalah pengembang frontend di BCS. Saya memulai perjalanan saya dengan tata letak antarmuka dengan berbagai kompleksitas dan selalu memberikan perhatian khusus pada antarmuka: betapa nyamannya bagi pengguna untuk berinteraksi dengannya, jika saya bisa menyampaikan kepada pengguna antarmuka yang tepat seperti yang diinginkan oleh perancang.
Dalam seri artikel ini saya ingin berbagi pengalaman saya menerapkan praktik fungsional dalam pengembangan frontend, saya akan berbicara tentang pro dan kontra yang akan Anda terima sebagai pengembang menggunakan praktik ini. Jika Anda suka temanya, maka kita akan terjun ke sudut yang “lebih kering” dan lebih kompleks dari dunia fungsional. Saya segera mencatat bahwa kita akan beralih dari yang lebih besar ke yang lebih kecil, yaitu, kita akan melihat aplikasi klasik dari pandangan mata burung, dan ketika kita membaca artikel-artikelnya, kita akan turun ke tempat praktik tertentu akan membawa kita manfaat yang nyata.
Jadi, mari kita mulai dengan menangani status. Pada saat yang sama saya akan memberi tahu Anda, apalagi, monad dan functors pada umumnya.
Intro
Ketika mengungkap antarmuka berikutnya dan menemukan titik temu antara UI dan analitik, saya mulai memperhatikan bahwa setiap kali seorang pengembang berurusan dengan jaringan, ia hanya perlu memproses semua keadaan UI dan menggambarkan reaksi terhadap keadaan tertentu. Dan karena masing-masing dari kita berjuang untuk keunggulan, ada keinginan untuk cara pemrosesan ini untuk mengeluarkan pola yang menggambarkan setransparan mungkin apa yang terjadi dan apa yang merupakan pemrakarsa dari reaksi tertentu, dan sebagai hasilnya, hasil dari pekerjaan. Untungnya, dalam dunia pemrograman, hampir semua yang Anda pikirkan diterapkan oleh seseorang sebelum Anda.
Baik di dunia pengembangan dan di dunia desain, tidak hanya pola yang terbentuk yang memungkinkan Anda untuk memecahkan masalah Anda secara efektif, tetapi juga antipatters, yang harus dihindari dengan segala cara agar praktik buruk tidak berkembang, dan pengembang atau perancang selalu memiliki pijakan dalam situasi, ketika tidak ada solusi konkret.
Dalam kasus kami, situasi yang dimiliki sebagian besar pengembang adalah pemrosesan semua keadaan elemen UI dan reaksi mereka. Masalahnya di sini adalah bahwa elemen UI dapat berinteraksi dengan keadaan lokal (tanpa menjalankan permintaan asinkron) dan dengan sumber daya atau repositori jarak jauh. Pengembang terkadang lupa untuk menangani semua kasus tepi, yang mengarah pada perilaku sistem yang tidak konsisten secara keseluruhan.
Semua contoh akan berisi contoh kode menggunakan perpustakaan Bereaksi dan superset JavaScript - TypeScript, serta perpustakaan untuk pemrograman fungsional fp-ts.
Pertimbangkan contoh paling sederhana, di mana kami memiliki daftar elemen yang kami minta dari server, dan kami harus menampilkan UI dengan benar sesuai dengan hasil permintaan. Kami tertarik pada fungsi
render , karena di dalamnya kita perlu menampilkan status yang benar selama eksekusi permintaan. Kode contoh lengkap dapat dilihat di:
aplikasi sederhana . Di masa depan, akan tersedia proyek yang lengkap, berfokus pada serangkaian artikel, di mana dalam kursus kita akan membongkar bagian-bagiannya masing-masing.
const renderInitial = (...) => ...; const renderPending = (...) => ...; const renderError = (...) => ... ; const renderSuccess = (...) => ... ; return ( {state.subcribers.foldL( renderInitial, renderPending, renderError, renderSuccess, )} );
Contoh tersebut dengan jelas menunjukkan bahwa setiap keadaan model data memiliki fungsi sendiri, dan setiap fungsi mengembalikan sebagian UI yang ditentukan untuknya (pesan, tombol, dll.).
RemoteData monad depan, saya akan mengatakan bahwa contoh menggunakan
RemoteData monad .
Itu sangat elegan, dan yang paling penting aman, kita dapat bekerja dengan data dan meresponsnya. Ini adalah pengantar, di mana saya mencoba menunjukkan manfaat dari pendekatan fungsional dalam contoh yang tampaknya sederhana.
Functor dan Monad
Sekarang, mari kita mulai secara bertahap menyelami teori kategori terapan dan menganalisis konsep-konsep seperti
Functor dan
Monad , dan juga mempertimbangkan praktik untuk bekerja dengan data secara aman menggunakan praktik fungsional.
“Pada dasarnya, functor tidak lebih dari struktur data yang memungkinkan Anda untuk menerapkan fungsi transformasi untuk mengekstrak nilai dari shell, memodifikasinya, dan kemudian memasukkannya kembali ke shell.
Menutup nilai dalam shell atau wadah adalah pola desain dasar dalam pemrograman fungsional, karena melindungi terhadap akses langsung ke nilai-nilai, yang memungkinkan mereka untuk dimanipulasi dengan aman dan tidak berubah dalam program aplikasi. "Saya mengambil kutipan ini dari
buku yang bagus
tentang ulasan teknik pemrograman fungsional dalam JavaScript . Mari kita mulai dengan komponen teoretis dan menganalisis apa sebenarnya functor itu. Untuk mulai dengan, kita perlu berkenalan dengan bagian yang menarik dari matematika yang disebut teori kategori di tingkat paling dasar.
Teori kategori adalah cabang matematika yang mempelajari sifat-sifat hubungan antara objek matematika, terlepas dari struktur internal objek. Teori kategori menempati tempat sentral dalam matematika modern, tetapi juga menemukan aplikasi dalam ilmu komputer, logika, dan fisika teoretis.Kategori terdiri dari objek dan panah yang diarahkan di antara mereka. Cara termudah untuk memvisualisasikan kategori adalah:
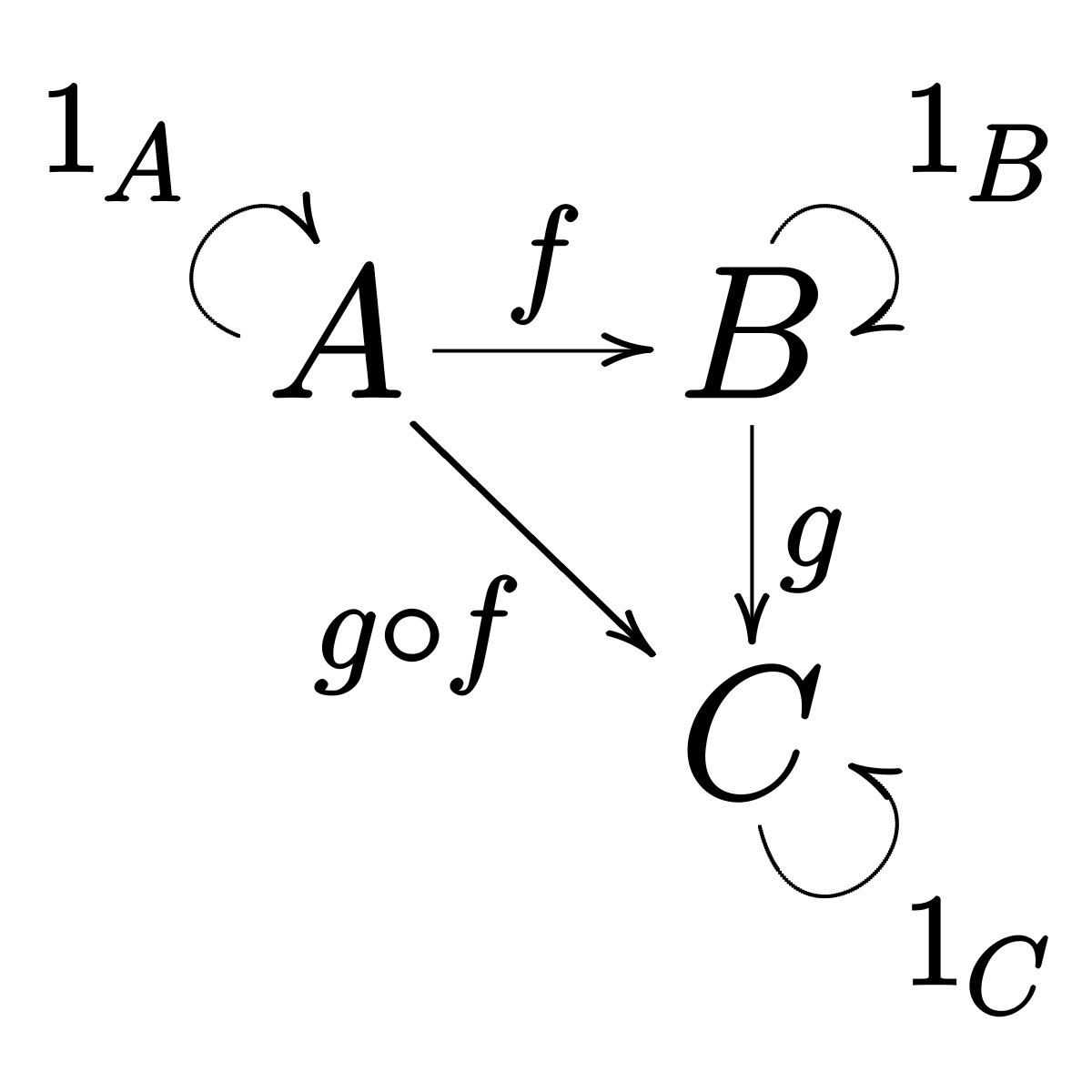
Panah diatur sehingga jika Anda memiliki panah dari objek
A ke objek
B dan panah dari objek
B ke
C , maka harus ada panah - komposisinya adalah dari
A ke
C. Pikirkan panah sebagai fungsi; mereka juga disebut morfisme. Anda memiliki fungsi
f yang mengambil A sebagai argumen dan mengembalikan B. Ada fungsi lain
g yang mengambil B sebagai argumen dan mengembalikan C. Anda dapat menggabungkannya dengan meneruskan hasil dari
f ke
g . Kami baru saja menggambarkan fungsi baru yang mengambil A dan mengembalikan C. Dalam matematika, komposisi seperti itu dilambangkan oleh lingkaran kecil antara notasi fungsi: g ◦ f. Perhatikan urutan komposisi - dari kanan ke kiri.
Dalam matematika, komposisi diarahkan dari kanan ke kiri. Dalam hal ini, akan membantu jika Anda membaca g ◦ f sebagai “g setelah f”.
-— A B f :: A -> B -— B g :: B -> C -— A C g . f
Ada dua sifat yang sangat penting yang harus dipenuhi komposisi dalam kategori apa pun.
- Komposisi bersifat asosiatif (asosiatif adalah properti operasi yang memungkinkan Anda untuk mengembalikan urutan eksekusi tanpa adanya indikasi eksplisit tentang suksesi dengan prioritas yang sama; ini membedakan antara asosiatif kiri, di mana ekspresi dievaluasi dari kiri ke kanan, dan asosiatifitas kanan dari kanan ke kiri. Operator yang sesuai disebut asosiatif kiri dan asosiatif kanan Jika Anda memiliki tiga morfisme (panah), f, g dan h, yang dapat diatur (yaitu, tipenya konsisten satu sama lain), Anda perlu tanda kurung untuk kelompok mereka. Secara matematis, ini ditulis sebagai
h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f (h ◦ g) ◦ f = h ◦ g ◦ f - Untuk setiap objek A ada panah, yang akan menjadi unit komposisi. Panah ini dari objek ke dirinya sendiri. Menjadi unit komposisi berarti ketika menyusun unit dengan panah apa pun yang dimulai pada A atau berakhir pada A, masing-masing, komposisi mengembalikan panah yang sama. Panah satuan dari objek A disebut IDa (unit pada A). Dalam notasi matematika, jika f beralih dari A ke B, maka
f ◦ idA = f
Untuk bekerja dengan fungsi, panah tunggal diimplementasikan sebagai fungsi yang identik, yang hanya mengembalikan argumennya.
Sekarang kita dapat mempertimbangkan apa fungsi dalam teori kategori.
Functor adalah jenis pemetaan khusus antar kategori. Ini dapat dipahami sebagai tampilan yang mempertahankan struktur. Fungsi antara kategori kecil adalah morfisme dalam kategori kategori kecil. Totalitas semua kategori bukan kategori dalam arti biasa, karena totalitas objeknya bukan kelas. -
Wikipedia .
Pertimbangkan contoh penerapan functor untuk wadah Maybe, yang merupakan gagasan "nilai yang mungkin tidak ada".
const compose = <A, B, C>( f: (a: A) => B, g: (b: B) => C, ): (a: A) => C => (a: A) => g(f(a)); // Maybe: type Nothing = Readonly<{ tag: 'Nothing' }>; type Just<A> = Readonly<{ tag: 'Just'; value: A }>; export type Maybe<A> = Nothing | Just<A>; const nothing: Nothing = { tag: 'Nothing' }; const just = <A>(value: A): Just<A> => ({ tag: 'Just', value }); // Maybe: const fmap = <A, B>(f: (a: A) => B) => (fa: Maybe<A>): Maybe<B> => { switch (fa.tag) { case 'Nothing': return nothing; case 'Just': return just(f(fa.value)); } }; // 1: fmap id === id namespace Laws { console.log( fmap(id)(just(42)), id(just(42)), ); // => { tag: 'Just', value: 42 } // 2: fmap f ◦ fmap g === fmap (f ◦ g) const f = (a: number): string => `Got ${a}!`; const g = (s: string): number => s.length; console.log( compose(fmap(f), fmap(g))(just(42)), fmap(compose(f, g))(just(42)), ); // => { tag: 'Just', value: 7 } }
Metode
fmap dapat dilihat dari dua sisi:
- Sebagai cara untuk menerapkan fungsi murni ke nilai "kemas";
- Sebagai cara untuk "meningkatkan konteks wadah" fungsi murni.
Memang, jika tanda kurung di antarmuka sedikit berbeda, kita bisa mendapatkan tanda tangan dari fungsi
fmap :
const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>);
Setelah mendefinisikan antarmuka:
type Function1<Domain, Codomain> = (a: Domain) => Codomain;
kami mendapatkan definisi
fmap :
const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>;
Trik sederhana ini memungkinkan kita untuk memikirkan functor sebagai cara untuk "meningkatkan fungsi murni ke dalam konteks wadah". Berkat ini, dimungkinkan untuk bekerja dengan berbagai jenis data dengan cara yang aman: misalnya, berhasil memproses rantai nilai tersarang opsional; Konversi daftar data menangani pengecualian dan banyak lagi.
Seperti dijelaskan sebelumnya, menggunakan functors, Anda dapat menerapkan fungsi ke nilai dengan aman dan tidak berubah. Monads mirip dengan functors, kecuali bahwa mereka dapat mendelegasikan logika khusus dalam kasus khusus. Functor sendiri hanya tahu cara menerapkan fungsi ini dan membungkus hasilnya kembali dalam sebuah shell, dan ia tidak memiliki logika tambahan.
Monad muncul saat membuat seluruh tipe data dengan prinsip mengekstraksi data dengan prinsip mengekstraksi nilai dari shell dan menentukan aturan dari nesting. Seperti halnya functors, monad adalah template desain yang digunakan untuk menggambarkan perhitungan dalam bentuk urutan tahapan di mana nilai yang diproses tidak diketahui sama sekali, tetapi monad yang memungkinkan untuk secara aman dan tanpa efek samping mengontrol aliran data saat digunakan dalam komposisi. Monads dapat ditujukan untuk memecahkan berbagai masalah. Secara teoritis, monad bergantung pada sistem tipe dalam bahasa tertentu. Bahkan, banyak orang berpikir bahwa mereka hanya dapat dipahami jika ada tipe data eksplisit.
Untuk lebih memahami monad, konsep penting berikut harus dipelajari.
Monad Menyediakan antarmuka abstrak untuk operasi monadik
Jenis monadik. Implementasi spesifik dari antarmuka ini
Tetapi contoh-contoh praktis dari penerapan sifat-sifat ini dari functor dan konstruksi kategoris lainnya akan saya tunjukkan dalam artikel mendatang.