Tentang koordinat barycentric di jari

Hai

Tentunya semua orang telah menyaksikan penilaian lubang intip tingkat kesamaan anak dengan orang tua: sesuatu seperti "ayah dicurahkan, tetapi dia tampak seperti ibu juga !!!"


( diambil dari sini )

Seperti pada contoh di gambar, Anda dapat mengevaluasi tingkat kesamaan dalam persen. Anda juga dapat menggunakan kerabat untuk lebih akurat menggambarkan wajah bayi dalam bentuk jumlah tertimbang kerabat kerabat ...

Dan itu akan terlihat dan dirasakan secara alami untuk orang "biasa" yang tidak terkait dengan antropologi, atau, misalnya, ilmu forensik. Untuk seorang profesional di bidang analisis dan pengenalan wajah, wajah manusia lebih cenderung seperangkat parameter. Yaitu, titik (seperangkat koordinat) di beberapa ruang dengan basis (sumbu yang sesuai dengan parameter). Dan jika kita menggambarkan wajah anak itu dibandingkan dengan saudara-saudaranya, maka kemungkinan besar titik yang sesuai dengan wajah anak itu akan muncul dalam ruang parameter di dalam lambung cembung dari awan titik yang sesuai dengan wajah saudara terdekat (tetapi ini tidak akurat).

Sebenarnya, apa yang saya semua tentang ... Kedua pendekatan untuk deskripsi wajah sesuai dengan dua sistem koordinat:

1. barycentric, deskripsi titik dalam ruang (dalam contoh kami: wajah) melalui campuran tertimbang dari titik-titik lain;
2. affine, deskripsi titik dalam ruang melalui koordinat dalam beberapa basis.

Jadi, apa itu koordinat barycentric?

Biarkan masuk -Dimensi ruang yang diberikan titik dengan vektor radius , . Selain itu, tidak ada titik yang terletak pada cangkang linier dari vektor radius titik yang tersisa ... Sederhananya, itu cukup sederhana: biarkan titik-titik ini membentuk sosok yang tidak dapat sepenuhnya direpresentasikan dalam ruang dengan dimensi kurang dari .

Dalam kasus ruang satu dimensi (garis), kita membutuhkan 2 titik non-kebetulan, dalam kasus ruang dua dimensi - segitiga non-degenerasi, dalam kasus tiga dimensi - tetrahedron.

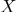
Lalu ada titik di luar angkasa dapat diwakili oleh vektor radius :



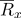
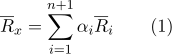
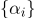
Setel dan ada koordinat barycentric.

Bagaimana koordinat barycentric lebih baik / lebih buruk dari affine?

Mari kita mulai dengan kerugian relatif:

1. dalam representasi barycentric, kita membutuhkan satu koordinat lebih dari yang affine;
2. jarak antara titik yang ditentukan secara barycentrically tidak dapat secara langsung dihitung dalam koordinat ini.

Sebagian, kelemahan pertama diimbangi oleh fakta bahwa meskipun perlu digunakan koordinat barycentric saat menggambarkan suatu titik di -Dimensi ruang, jumlah derajat tidak bertambah. Koordinat barycentric yang didefinisikan dalam rumus (1) terkait dengan relasi:



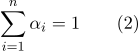
Adapun kelemahan kedua, jika ada kebutuhan untuk menghitung jarak antara titik-titik yang diwakili barycentrically, maka masuk akal untuk menghitung produk skalar dan gunakan analog dari jarak Mahalanobis.

Apa bonus dari menggunakan koordinat barycentric?

1. Koordinat barycentric invarian dengan transformasi affine ruang. Properti ini digunakan, misalnya, untuk interpolasi linier dalam grafik komputer. Biarkan koordinat tekstur didefinisikan pada simpul elemen permukaan segitiga 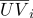dan normals ( 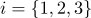), maka setiap titik dari bagian permukaan ini akan memiliki koordinat barycentric 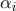koordinat teksturnya 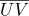dan normal 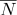dapat dihitung sebagai:
   
   
   
   
   
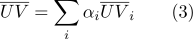
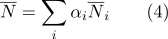
2. Dengan koordinat barycentric, mudah untuk menentukan apakah suatu titik termasuk 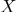bagian-bagian ruang yang dibatasi oleh polyhedron dengan simpul : ini hanya dilakukan jika . Kesetaraan koordinat barycentric ke-1 berarti bahwa intinya bertepatan dengan . Jika beberapa koordinat barycentric sama dengan 0, maka ini berarti bahwa titik tersebut milik subruang yang direntang oleh vektor radius titik-titik yang tersisa yang koordinatnya lebih besar dari 0.

Mungkin mereka sangat sulit untuk dihitung?

Tidak lebih rumit daripada transformasi linear dari sistem koordinat. Karena, pada dasarnya, perhitungan koordinat barycentric adalah suatu transformasi.

Kami menulis ulang vektor jari-jari titik dalam bentuk berikut:

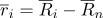
dimana - vektor radial dalam sistem koordinat yang berpusat pada suatu titik .

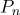
Maka rumus (1) dapat ditulis ulang dalam bentuk berikut:



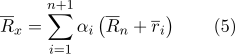
Kami akan mengungkapkan tanda kurung dalam jumlah:



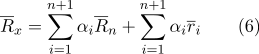
Menurut properti (2):



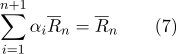
Oleh karena itu:

,

dimana

Mengingat (2), kami membatasi diri untuk menghitung koordinat n barycentric pertama. Bayangkan transisi ke koordinat barycentric sebagai transformasi linear:

,

dimana - vektor n dari koordinat barycentric (kecuali yang terakhir), - matriks transformasi.

Mengingat sifat-sifat representasi barycentric, jika sebagai ganti salah satu vektor ( ), maka kita mendapatkan vektor dengan nol komponen, kecuali satu ke-satu, yang akan sama dengan 1.

Jika matriks kalikan dengan matriks terdiri dari kolom dari , maka kita harus mendapatkan matriks identitas (matriks dengan yang ada di diagonal utama dan nol di elemen yang tersisa):

,

dimana , Apakah matriks identitas ( - Simbol Kronecker: 1 jika jika tidak 0).

Dari (10) kami temukan :



Dengan demikian, memiliki satu set titik dengan jari-jari vektor , kita dapat menghitung matriks untuk dikonversi ke koordinat barycentric:



Dengan menggunakan matriks ini, kita bisa mendapatkan yang pertama titik koordinat barycentric dengan radius vektor :



Menggunakan relasi (2) lagi, kita mendapatkan koordinat barycentric terakhir:

Kesimpulan

Mungkin sekilas, barycentric juga tampak canggung dan kompleks. Tetapi pada kenyataannya, ini adalah alat yang sangat nyaman dan sangat diperlukan dalam banyak tugas, yang Anda terbiasa dengan cukup cepat. Karena tidak ada sihir di sini, itu adalah aljabar linier dalam bentuknya yang paling murni!