Regresi Linier dan Keturunan Gradien

Biarkan indikator X dan Y, yang memiliki ekspresi kuantitatif, dipelajari dalam bidang subjek tertentu.

Selain itu, ada setiap alasan untuk percaya bahwa indikator Y tergantung pada indikator X. Posisi ini dapat menjadi hipotesis ilmiah dan didasarkan pada akal sehat dasar. Misalnya, ambil toko bahan makanan.

Ditunjukkan oleh:

X - area penjualan (sq. M.)

Y - omset tahunan (juta p.)

Jelas, semakin tinggi area perdagangan, semakin tinggi omset tahunan (kami mengasumsikan hubungan linier).

Bayangkan kita memiliki data pada beberapa n store (ruang ritel dan omset tahunan) - dataset dan ruang ritel k (X), yang ingin kita prediksi omset tahunan (Y) adalah tugas kita.

Kami berhipotesis bahwa nilai Y kami bergantung pada X dalam bentuk: Y = a + b * X

Untuk menyelesaikan masalah kita, kita harus memilih koefisien a dan b.

Pertama, mari kita menetapkan nilai acak a dan b. Setelah itu, kita perlu menentukan fungsi kerugian dan algoritma optimasi.

Untuk melakukan ini, kita dapat menggunakan fungsi root mean square loss ( MSELoss ). Itu dihitung dengan rumus:



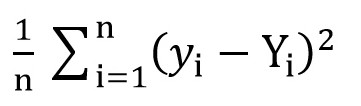
Di mana y [i] = a + b * x [i] setelah a = rand () dan b = rand (), dan Y [i] adalah nilai yang benar untuk x [i].
Pada tahap ini, kita memiliki standar deviasi (fungsi tertentu a dan b). Dan jelas bahwa, semakin kecil nilai fungsi ini, semakin tepat parameter a dan b dipilih sehubungan dengan parameter yang menggambarkan hubungan yang tepat antara area ruang ritel dan omset di ruangan ini.

Sekarang kita dapat mulai menggunakan gradient descent (hanya untuk meminimalkan fungsi kerugian).

Keturunan gradien

Esensinya sangat sederhana. Misalnya, kami memiliki fungsi:

y = x*x + 4 * x + 3 

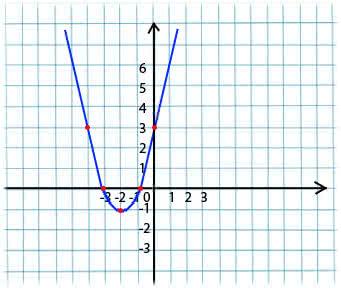
Kami mengambil nilai x sewenang-wenang dari domain definisi fungsi. Bayangkan ini adalah poin x1 = -4.

Selanjutnya, kita mengambil turunan sehubungan dengan x fungsi ini pada titik x1 (jika fungsi tergantung pada beberapa variabel (misalnya, a dan b), maka kita perlu mengambil turunan parsial untuk masing-masing variabel). y '(x1) = -4 <0

Sekarang kita mendapatkan nilai baru untuk x: x2 = x1 - lr * y '(x1). Parameter lr (learning rate) memungkinkan Anda untuk mengatur ukuran langkah. Jadi kita mendapatkan:

Jika turunan parsial pada titik tertentu x1 <0 (fungsi menurun), maka kita pindah ke titik minimum lokal. (x2 akan lebih besar dari x1)

Jika turunan parsial pada titik tertentu x1> 0 (fungsi meningkat), maka kita masih bergerak ke titik minimum lokal. (x2 akan kurang dari x1)

Dengan melakukan algoritma ini secara berulang, kami akan mendekati minimum (tetapi tidak akan mencapainya).

Dalam praktiknya, ini semua terlihat jauh lebih sederhana (namun, saya tidak berani mengatakan koefisien a dan b mana yang paling cocok dengan case di atas dengan toko, jadi kami mengambil ketergantungan pada bentuk y = 1 + 2 * x untuk menghasilkan dataset, dan kemudian melatih model kami pada dataset ini):
(Kode ditulis di sini )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

Setelah mengkompilasi kode, Anda dapat melihat bahwa nilai awal a dan b masing-masing jauh dari yang diminta 1 dan 2, dan nilai akhir sangat dekat.

Saya akan menjelaskan sedikit mengapa a_grad dan b_grad dianggap demikian.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . Turunan parsial dari F berkenaan dengan akan -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . Turunan parsial dari F sehubungan dengan b adalah -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . Kami mengambil nilai rata-rata (mean()) karena error dan x_train dan y_train adalah array nilai, a dan b adalah skalar.

Bahan yang digunakan dalam artikel:

menujudatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html