Geekly articles weekly

Angka yang mendasari musik modern


Mengapa dua belas?


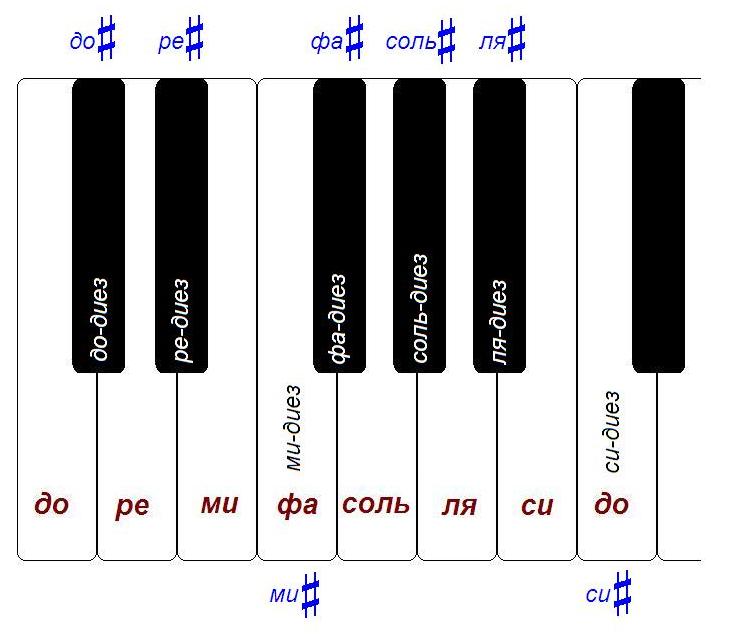
Jika Anda melihat keyboard, Anda akan melihat bahwa setiap oktaf berisi 12 semitone.
Dalam hal piano, ini hanya berarti bahwa antara, misalnya, "ke" oktaf pertama dan "ke" oktaf kedua, ada 11 kunci. Bersama dengan salah satu "lakukan" (misalnya, ke oktaf kedua) kita mendapatkan 12 kunci: lakukan #, kembali, kembali #, mi, fa, fa #, garam, garam #, la, la #, si, lakukan.


Tapi mengapa 12?


Mungkin ini hanya kecelakaan? Nenek moyang kita menyukai angka 12, mereka memiliki 12 di mana-mana: 12 bulan, 12 tanda zodiak, 12 suku Israel, 12 rasul, ... dan di sini mereka memutuskan, biarlah 12, dan demikianlah diperintahkan. Atau apakah masih ada hukum yang obyektif, dan angka ini tidak disengaja?


Pada artikel ini saya akan mencoba menunjukkan bahwa ini bukan kecelakaan. Persyaratan yang cukup umum, cukup alami untuk musik modern (barat), dengan kebutuhan matematika, membawa kita ke nomor 12. Sangat menarik bahwa alasan mengapa kita memiliki nilai ini adalah milik nomor lain (lihat bagian akhir artikel). Anda bahkan dapat mengatakan bahwa itu terletak di jantung suara modern.


Pernyataan masalah


Pertama, mari kita coba memformalkan tugas.


Kami memiliki frekuensi referensi $ \ omega_0 $ . Kami akan menyebutnya tonik. Kami juga memiliki satu oktaf dengan frekuensi $ 2 \ omega_0 $ . Sekarang kita perlu memahami opsi apa untuk frekuensi menengah $ \ omega_0 $ sebelumnya $ 2 \ omega_0 $ , sedemikian sehingga melodi yang dibangun di atas nada-nada ini akan terdengar harmonis untuk telinga kita?


Saya takut formulasi ini, meskipun mencerminkan esensi dari pertanyaan, masih, dari sudut pandang matematika, agak kabur, dan pertanyaan seperti itu tidak dapat dijawab dengan tegas, jika hanya karena pendengaran manusia memiliki resolusi frekuensi yang agak terbatas. Dan ini dikonfirmasi oleh fakta bahwa pada waktu yang berbeda digunakan nada yang berbeda, misalnya, Pythagoras , lagu yang bersih , mudah marah , dan mudah marah . Dan mereka semua terdengar dan terdengar, setidaknya untuk pekerjaan tertentu, cukup dapat diterima.


Apa itu harmoni?


Kami harus memberlakukan beberapa ketentuan tambahan. Tetapi pertama-tama, kita harus menjawab satu pertanyaan penting: apa yang kita anggap sebagai suara yang harmonis?


Mari kita lihat dua suara - dengan frekuensi $ \ omega_1 $ dan $ \ omega_2 $ .


Ambil perbandingan frekuensi ini. Hubungan ini dapat direpresentasikan sebagai produk angka $ a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l} $ dimana $ a_1, a_2, ..., a_l $ Apakah bilangan prima, dan $ k_1, k_2, ..., k_l $ - bilangan bulat, misalnya, rasio ini mungkin sama $ 2 ^ {- 3} \ cdot3 \ cdot5 $ . Dan dari bilangan prima ini ( $ a_1, a_2, ..., a_l $ ) kurang, semakin harmonis untuk telinga kita interval ini akan berbunyi (saya menemukan pernyataan ini di sini (lihat paragraf kedua) )


Jadi, misalnya, suara yang paling harmonis sesuai dengan pernyataan ini adalah satu oktaf (frekuensi berganti 2 kali). Dan interval harmonik berikutnya akan menjadi yang kelima (perubahan frekuensi dalam $ 3/2 $ kali) dan satu liter (perubahan frekuensi dalam $ 4/3 $ kali).


Namun tidak sesederhana itu dengan pernyataan ini. Jadi, misalnya, tidak terlalu jelas bagaimana derajatnya mempengaruhi. Misalnya, perkalian yang lebih harmonis dengan $ 3 ^ 2 $ atau 7? Saya tidak tahu apakah pertanyaan ini telah dipelajari atau belum, dan apakah mungkin, secara prinsip, memberikan jawaban untuk pertanyaan itu. Juga, persepsi harmoni adalah hal yang agak subyektif. Jadi, musik modern penuh dengan suara yang akan dianggap sebagai hiruk-pikuk yang mengerikan selama 100-200 tahun.


Kondisi pertama. Tonik, Quart, Quint, Oktaf


Ketidakpastian ini bukan masalah bagi penelitian kecil kami. Faktanya adalah bahwa satu-satunya kesimpulan yang ingin saya tarik dari pernyataan ini adalah bahwa dalam kasus kami, dalam hal apa pun, setidaknya harus ada interval "paling harmonis", yaitu, satu oktaf, satu liter dan seperlima. Artinya, bersama dengan tonik dengan frekuensi $ \ omega_0 $ dan oktaf dengan frekuensi $ 2 \ omega_0 $ kita juga harus memiliki yang kelima dan keempat, dengan frekuensi masing-masing $ {3 \ lebih dari 2} \ omega_0 $ , $ {4 \ lebih dari 3} \ omega_0 $ atau sesuatu yang sangat dekat yang kita tidak bisa membedakan dari yang kelima murni dan keempat.


Catatan: pada kenyataannya, hanya tonik, perlima dan oktaf cukup. Kehadiran seperlima segera memberi kita satu liter, sebagai tambahan satu oktaf, dan berdasarkan kondisi kedua (invarian), yang dijelaskan di bawah ini, kita juga harus memiliki satu liter dan tonik. Artinya, kebutuhan untuk satu liter adalah konsekuensi dari kehadiran yang kelima dan persyaratan invarian.


Dan ini adalah persyaratan pertama kami.


Kondisi kedua. Invarian


Persyaratan kedua kami adalah invarian. Dan ini merupakan persyaratan penting dari musik modern. Persyaratan ini terdiri dari kenyataan bahwa semua harmoni pada tombol apa pun harus terdengar sama. Jika kita berbicara tentang sistem modern, yang digunakan untuk menyetel piano, maka ini berarti bahwa nada kelima, yang terdiri dari tujuh setengah nada, harus terdengar sama, terlepas dari apa suaranya. Artinya, rasio frekuensi antara do dan salt harus sama dengan do # - salt #, re-la, re #-la #, ... dan sama $ 3/2 $ . Dan invarian ini harus berlaku, tentu saja, tidak hanya untuk yang kelima, tetapi juga untuk setiap interval. Keuntungan penting dari sistem ini adalah kemampuan untuk mentransposisikan permainan pada interval apa pun. Ini adalah esensi dari temperamen yang seragam.


Saya harus mengatakan bahwa persyaratan invarian ini tidak begitu jelas, dan pendekatan ini baru-baru ini diterapkan, hanya pada abad ke-18. Sistem yang digunakan sebelumnya (misalnya, Pythagoras dan murni) tidak memiliki properti seperti itu. Misalnya, dengarkan Sonata untuk Microtonal Piano (Ben Johnston) , yang ditulis dalam sistem yang bersih (batas utama = 5). Rasanya seperti piano tidak disetel. Semua kekayaan harmoni modern didasarkan tepat pada invarian ini. Misalnya, Bach "Well-Tempered Clavier" muncul dengan tepat berkat pendekatan baru untuk menyetel keyboard. Keanehan inilah yang memungkinkan Bach untuk menciptakan urutan harmonis yang sebelumnya tidak mungkin.


Jadi, sekarang kita memiliki semua data yang diperlukan untuk perhitungan.


Perhitungan


Mari kita membangun skala dari tonik hingga oktaf yang memenuhi kedua persyaratan.
Misalkan dalam kasus ini kita dapatkan $ N $ suara (termasuk satu oktaf). Itu $ N $ dan merupakan nomor yang diinginkan. Kami ingin menunjukkan itu $ N $ dalam kondisi kami harus 12.


Konsekuensi dari persyaratan kedua adalah bahwa interval antara frekuensi suara tetangga harus sama dan sama $ 2 ^ {1 \ lebih dari N} $ .


Sekarang persyaratan pertama mengatakan bahwa di baris kita harus ada dua suara yang sesuai dengan (dengan perkiraan yang baik) frekuensi $ {3 \ lebih dari 2} \ omega_0 $ dan $ {4 \ over3} \ omega_0 $ . Ini yang kelima dan keempat. Misalkan satu liter adalah $ n_1 $ terdengar di baris kami, dan yang kelima - $ n_2 $ oh Kami menunjukkan $ n = n_2 - n_1 $ .


Sangat mudah untuk melihat bahwa perubahan frekuensi antara yang keempat dan kelima (rasio frekuensi) adalah $ 9/8 $ .


Tetapi, menurut kondisi kedua kami, ini juga harus sama $ 2 ^ {n \ lebih dari N} $ .


Jadi kami mendapat formula:


$ 2 ^ {n \ lebih dari N} \ sekitar 9/8 $


Setelah transformasi sederhana, kami mendapatkan rumus dasar:


$ n \ approx N (2 \ log_2 {3} - 3) = N \ cdot 0,170 $


Sangat mudah untuk melihat bahwa solusinya (tentu saja, perkiraan) $ N = 6i $ dimana $ i $ - angka berapa pun secara alami (cukup kecil, karena bagaimanapun 0,170 berbeda dari 1/6).


Mari kita lihat sebuah kasing $ i = 1 $ . Dalam hal ini $ N = 6 $ , $ n = 1 $ . Artinya, ini adalah varian dari sistem modern, hanya tanpa setengah nada, hanya dengan nada (do, re, mi, fa #, salt #, la #, do). Tetapi, seperti yang Anda lihat, dalam hal ini quart (f) dan quint (salt) tidak termasuk dalam skala ini.


Yaitu, satu-satunya pilihan bagi kita


$ N = 12 i $ dimana $ i $ - setiap nomor alami ( $ i $ cukup kecil). Kasing $ i = 1 $ hanya sesuai dengan sistem modern kita, yang disebut sistem temperamental yang seragam.


Tetapi mengapa tidak 24 atau lebih? Alasannya sederhana - saya dapat berasumsi bahwa kelulusan seperti itu sudah berlebihan untuk persepsi kita. Karena itu, hanya satu nomor yang tersisa: 12.


Jika Anda tidak puas dengan pemikiran yang diberikan, maka di sini Anda dapat menemukannya


bukti matematika yang ketat

Tantangan:


Temukan bilangan bulat positif minimum N di mana ada bilangan bulat positif $ n <N $ sedemikian rupa $ 2 ^ {n \ lebih dari N} $ berbeda dari $ 3 \ lebih dari $ 2 tidak lebih dari $ \ delta $ sen .


Solusi:


Ditunjukkan oleh $ Z_n = N \ cdot (log_2 {3} -1) $ . Lalu, dengan $ \ delta <{1200 \ over N} $ (Yang berlaku untuk kisaran itu $ \ delta $ dan $ N $ yang akan kami pertimbangkan) tugas kami adalah menemukan minimum $ N $ dimana


$ {1200 \ over N} \ cdot | Z_n - round (Z_n) | <\ delta $ ,


dimana $ putaran $ - fungsi pembulatan ke bilangan bulat terdekat.


Kami akan menyelesaikan masalah ini secara numerik.


gambar


Sekarang saatnya memutuskan $ \ delta $ .


Berapa jumlah (dalam sen) dari perbedaan antara kelima murni dan "kelima kami" yang kami anggap dapat diterima? Banyak orang mendengar, misalnya, bahwa sepertiga besar / kecil dalam sistem yang dikontrol secara merata "palsu". Tetapi ini hanya sekitar 15 sen relatif terhadap interval murni. Karena itu, persyaratan kami harus lebih baik dari 15 sen. Beberapa sumber mengatakan bahwa pada frekuensi tertentu, musisi membedakan hingga 5 - 6 sen. Karena itu bijaksana untuk mengambil $ \ delta = 5 $ .


Kemudian tabel dengan jelas menunjukkan bahwa yang terkecil $ N = 12 $ . Berikut ini memuaskan $ N = 17,24,29,34,36,41, ... $ .


Catatan:
Iterasi berikutnya, untuk masing-masing $ N $ Anda juga perlu memeriksa suara dan interval lainnya. Dalam hal $ N = 17 $ misalnya, pertiga menjadi sepenuhnya "palsu": lebih dari 30 sen (untuk sepertiga besar).


Jadi jawaban kita adalah: $ N = 12 $ . Yang harus dibuktikan.


Dan omong-omong, sudah jelas bahwa jawaban kami tidak akan berubah jika sebaliknya $ \ delta = 5 $ ambil, misalnya, 10 atau bahkan 15.


Kesimpulan Nomor yang mendasari


Yang mengejutkan, ternyata angka yang mendasari sistem musik modern dan musik kontemporer (Eropa) adalah $ \ log_2 {3} $ , yaitu, bahwa dengan akurasi yang baik (0,1%) persamaan berikut berlaku:


$ \ log_2 {3} \ sekitar 19/12 $


Tanggapan terhadap komentar dan kritik dalam komentar

Pertama-tama, terima kasih atas komentarnya yang menarik!
Inilah jawaban saya atas komentar dan kritik paling penting (menurut saya).


Kritik 1. Telur atau ayam


Druu: Lihat, 12 suara dalam satu oktaf sampai dengan temperamen yang seragam secara umum, jadi Anda tidak dapat membenarkan 12 suara dengan bantuan temperamen, ini hanya salah.


sarang: Ini persis logika dering yang saya bicarakan: jika Anda memilih musik yang dibangun pada sistem tertentu, jelas bahwa dalam konteksnya sistem yang berbeda tidak mungkin.


Untuk komentar-komentar ini dan yang sejenis, saya akan mengutip 2 bantahan:


1) jika dengan akurasi yang cukup kesetaraan $ log_2 {3} = 19/12 $ , maka tidak mungkin untuk "menarik" sistem temperamen seragam ke dalam sistem murni yang terdiri dari 12 suara. Semakin kuat $ log_2 {3} $ berbeda dari $ 19/12 $ , semakin keliru suara kelima kita. Jika jumlah ini (sangat) berbeda, maka tidak akan ada pendekatan temperamental seragam untuk interval murni, dan, sebagai hasilnya, tidak akan ada musik modern atau, katakanlah, itu akan berbeda. Oleh karena itu, kesimpulan bahwa sifat-sifat angka tersebut cukup logis $ log_2 {3} $ adalah dasar dari musik modern.


2) bantahan kedua tidak mungkin dibenarkan secara logis, dan hanya sebuah asumsi, tetapi bagi saya tampaknya semua alasan ini patut diperhatikan. Mari kita coba menjawab pertanyaan, mengapa kebutuhan untuk sistem yang diwarnai seragam muncul sama sekali? Komentar sudah dijawab sebagian. Musik pada waktu itu (saat menciptakan sistem temperamental seragam) sudah menggunakan modulasi dan polifoni, yang pada kenyataannya, pada umumnya, sudah membutuhkan temperamen seragam. Masalah suara "palsu" diselesaikan oleh fakta bahwa musisi sedikit "menyesuaikan" suara selama pertunjukan. Itu mudah dilakukan untuk string (setidaknya fretless), angin dan vokal (benar, jika saya salah - saya membuat kesimpulan ini dari komentar Anda). Misalnya, untuk biola - ini hanya sedikit perubahan posisi jari. Tapi begitu Anda kehilangan kesempatan seperti itu (harpsichord), maka segera semuanya mulai terdengar buruk. Jadi, sepertinya 12 not ini muncul tidak hanya seperti itu, tetapi sebagai perkembangan alami dari musik terhadap kemungkinan modulasi gratis dan polifoni yang kaya, dan ini pada gilirannya merupakan konsekuensi dari invarian. Itu adalah perkembangan alami dari musik. Yaitu, saya ingin mengatakan bahwa jika invarian matematis dimungkinkan bukan untuk 12 suara, tetapi, misalnya, untuk 10, maka kita (bahkan sebelum temperamen seragam) dalam skala kita akan memiliki 10 suara (dalam hal ini, saya sedang berbicara tentang cara perkembangan musik Eropa). Dan kemudian 10 suara temperamen seragam akan ditarik ke sistem murni kita.


Kritik 2. Keunikan dua belas


Ada banyak kritik tentang klaim bahwa 12 adalah satu-satunya angka yang masuk akal.


Pertama, memahami agresivitas pernyataan ini dan prinsip ketidakmungkinan pembenaran yang ketat, saya mungkin mengurangi tingkat kategorisasi beberapa tuduhan dalam artikel tersebut. Namun ...


Dalam hal ini, kami memiliki 2 baris kritik.


1) Mengapa saya menganggap 19, 24 atau 29 (dll.) Tidak dapat diterima?


Tidak, kurasa tidak. Untuk instrumen yang berbeda, ada teknik untuk menggunakan suara di luar skala, misalnya, glissando dan vibrato. Teknik-teknik ini menambah keindahan dan kealamian pada suara. Oleh karena itu, bahkan dengan 12 catatan kami masih menggunakan suara tambahan. Jika kita berbicara tentang lingkungan, tentang suara yang tidak biasa, tentang memperkaya suara ... maka ini cukup dibenarkan, tetapi jika kita berbicara tentang nada dasar, maka saya ragu. Musik diciptakan tidak hanya untuk elit, tetapi untuk orang biasa, dan bagi mereka kelulusan seperti itu (IMHO) tidak perlu.


Argumen kedua, dan itu diberikan dalam komentar, memang, memang kompleksitas menciptakan instrumen dan kinerja dalam kasus skala panjang, meskipun kami memiliki contoh yang bagus dari instrumen tersebut - sitar. Tetapi cobalah untuk mengambil satu oktaf (dengan satu tangan) pada piano jika Anda memiliki skala 24 suara.


2) Tetapi bagaimana dengan pentatonik?


Di semua negara timur tempat saya berada, untuk beberapa alasan saya sangat jarang mendengar musik nasional yang dibangun pada skala pentatonik. Dan semua musisi dari timur, yang saya dengarkan (dan saya suka beberapa), juga menampilkan musik Eropa. Berikut ini kutipan yang menarik: "Komposer akademis telah menggunakan pentatonis sebagai cat khusus sejak abad ke-19 untuk memberi musik rasa yang kuno." Aroma kuno ...
Namun dalam persepsi saya, musik ini tidak modern, tetapi saya tidak ingin mempertahankan posisi ini, jadi di beberapa tempat dalam artikel saya menggunakan istilah "musik Eropa modern". Jelas bahwa musik ini (dibangun pada skala pentatonik) dikembangkan sesuai dengan undang-undang lain, dan tidak mencapai permintaan polifoni yang kaya dan modulasi yang sering dan mudah, yang muncul dalam musik Eropa. Karena itu, artikel ini jelas bukan tentang pentatonik.


Kritik 3. Musik kontemporer


Apa yang saya sebut musik modern?


Walaupun ini terdengar seperti tautologi, oleh musik modern yang saya maksud adalah musik yang memerlukan invarian, yang dalam kasus instrumen dengan sistem tetap (misalnya, harpsichord, piano) mengarah pada kebutuhan untuk sistem beriklim seragam (atau sesuatu yang dekat). Dalam kasus instrumen lain, misalnya, senar fretless, semuanya terlihat sedikit lebih rumit, karena, pada kenyataannya, dimungkinkan untuk menggunakan seperangkat suara yang lebih besar (dari 12). Tapi tetap saja, ketika kita berbicara tentang persyaratan invarian, kita berarti bahwa suara-suara ini harus sangat dekat (dalam frekuensi) dengan 12 kita.


Definisi ini mencakup hampir semua musik piano, klasik Eropa, jazz, musik rock, pop, dan semua turunannya. Saya yakin ada pengecualian, tapi IMHO ini pengecualian. Saya tidak melihat alasan untuk berdebat tentang ini, karena setiap orang dapat menginvestasikan sesuatu dalam konsep ini.


Kritik 4. Perhitungan


Kesalahan dalam perhitungan.


Saya pikir pertanyaan ini dihapus. Namun, saya harus mengakui bahwa dalam pembahasan saya membuat beberapa pernyataan yang salah tentang hal-hal sekunder yang tidak mempengaruhi kesimpulan utama artikel.


PS Jangan memperlakukan artikel ini (dan menyajikan persyaratan yang relevan) sebagai karya akademis. :) Ini bukan artikel tentang teori musik. Apalagi ini bukan artikel tentang sejarah musik. Dalam bidang-bidang ini, saya sama sekali tidak menganggap pengetahuan saya paling tidak penting dan mengakui bahwa mungkin ada ketidakakuratan, meskipun saya mencoba menghindarinya. Di sini masalah matematika sederhana dirumuskan (dari tingkat kompleksitas sekolah), solusinya, menurut saya, memiliki interpretasi yang menarik. Dengan yang saya bagikan.

Source: https://habr.com/ru/post/id471600/

More articles:


All Articles