Cinta matematika

Berdasarkan sebuah artikel oleh Julien Clinton Sprott. Model cinta yang dinamis. Psikologi dan Ilmu Hayati Dinamika Nonlinier, Agustus 2004.

Saya percaya harmoni dalam aljabar ...
Teori teman saya kering, tetapi pohon kehidupan selalu hijau ...

Siapa yang tidak mempermasalahkan "masalah" ini .... Itu dibongkar dalam tragedi Yunani kuno, Shakespeare yang hebat menceritakan kepada kita kisah Romeo dan Juliet, Andrzej Wajda membongkarnya dari kedua sisi dalam Anatomi Cinta. Tetapi orang-orang tidak pernah sampai pada dasar kebenaran sampai para ilmuwan mengambil keputusan. Benar, tidak semuanya tampak cukup meyakinkan bagi psikolog. Mereka sendiri kadang-kadang bahkan setelah perceraian mereka sendiri mulai menganalisis sejarah cinta mereka yang sudah pergi. Ya, tulis buku yang terkadang seperti kue panas. Mereka ditulis oleh para ahli! Apa yang bisa saya katakan? Hampir bukan masalah pribadi - hanya bisnis ...

Dan akhirnya, bukan penyair dengan penulis dan psikolog yang suka bercinta. Matematika adalah ratu ilmu. Apakah dia mampu mengatasi masalah kekal? Buku-buku diterbitkan, misalnya, oleh John Gotman, "The Mathematics of Marriage," dan penulis lainnya. Matematikawan menganggap pengembangan hubungan romantis sebagai proses dinamis ...

Dan semuanya dimulai, seperti yang diharapkan, dengan definisi. Bagaimana cara mengidentifikasi cinta secara kualitatif dan kuantitatif? Peneliti mengklasifikasikan masalah berdasarkan jenis: hubungan cinta, gairah, kesetiaan. Selain itu, setiap spesies memiliki serangkaian perasaan yang kompleks. Tapi selain cinta untuk orang lain, ada cinta untuk diri sendiri, untuk hidup, untuk kemanusiaan ...

Pada saat yang sama, kebalikan dari cinta - dalam model matematika - tidak dapat dibenci, karena kedua perasaan ini dapat hidup berdampingan pada saat yang sama. Misalnya, seseorang mungkin menyukai beberapa manifestasi dari pasangan, tetapi yang lain mungkin jahat. Oleh karena itu, tidak realistis untuk mengasumsikan bahwa cinta seorang individu hanya dipengaruhi oleh perasaannya sendiri, dan perasaan pasangan lain tidak tergantung pada pengaruh lain, dan bahwa parameter yang menandai interaksi dua orang tetap tidak berubah dan dengan demikian mengecualikan kemungkinan belajar dan adaptasi.

Kompleksitas bahkan dalam model terbatas minimal meningkat secara dramatis ketika tiga atau lebih variabel dimasukkan ke dalam persamaan nonlinier dan / atau.

* Catatan: penerjemah. Menurut pendapat saya, studi tersebut juga dapat menghidupkan kembali matematika itu sendiri, menarik perhatian publik, biasanya terasing dari ilmu abstrak ini.

Model linier sederhana

Kisah cinta Romeo dan Juliet dalam waktu (t) dapat direpresentasikan menggunakan fungsi * R (t) - Cinta Romeo untuk Juliet dan J (t) - Cinta Juliet untuk Romeo.

Kemudian model linier sederhana dari hubungan mereka diungkapkan oleh persamaan (1)



a dan b - parameter gaya romantis Romeo
Pilihan gaya c dan d - Juliet
a - mencirikan bagaimana Romeo diselimuti perasaannya sendiri
b - seberapa besar Romeo dirangkul oleh perasaan Juliet

Salah satu artikel (Gottman et al., 2002) menggunakan istilah "inersia perilaku" untuk yang pertama dan "fungsi pengaruh" untuk parameter kedua. Meskipun pada a = 0, inersia menjadi terbesar. Model dinamis dalam kondisi seperti itu adalah dua dimensi dan dapat dikendalikan oleh kondisi awal dan empat parameter, yang bisa positif atau negatif.

Model linier sederhana diusulkan oleh Rinaldi, 1998a. Pada saat yang sama, istilah bebas ditambahkan ke masing-masing turunan untuk memperhitungkan daya tarik (atau antipati dengan nilai negatif), yang ditunjukkan masing-masing mitra kepada yang lain tanpa adanya perasaan lain. Model seperti itu lebih realistis karena memungkinkan perasaan tumbuh dari keadaan acuh tak acuh dan memberikan keseimbangan yang tidak ditandai dengan apatis penuh. Semua ini dijelaskan dengan cara ini hanya dengan memasukkan dua parameter tambahan. Sementara keadaan keseimbangan non-apatis dapat menjadi sangat penting bagi individu yang bersangkutan, ini tidak mengubah dinamika selain dari dengan memindahkan ruang keadaan RJ.

Gaya romantis

Romeo dapat menunjukkan salah satu dari empat gaya romantis tergantung pada tanda a dan b, dengan notasi yang diberikan oleh penulis karya (Strogatz, 1994) dan murid-muridnya:

1. Keinginan besar: a> 0, b> 0 (Romeo diselimuti perasaan dan perasaan Juliet sendiri.)
2. Tipe narsis: a> 0, b <0 (Romeo lebih diselimuti perasaannya sendiri, ia terlepas dari perasaan Juliet.)
3. Cautious (atau kekasih yang dapat diandalkan): a <0, b> 0 (Romeo menjauh dari perasaannya sendiri, tetapi ia dikalahkan oleh perasaan Juliet.)
4. Hermit: a <0, b <0 (Romeo terlepas dari perasaan dan perasaan Juliet sendiri.)

Karena empat gaya perilaku juga dimungkinkan untuk Juliet, ada 16 kemungkinan kombinasi pasangan, masing-masing dengan dinamikanya sendiri, meskipun setengahnya sesuai dengan permutasi R dan J.

Persamaan (1) menentukan titik ekuilibrium tunggal untuk R = J = 0, yang sesuai dengan hubungan yang saling acuh tak acuh, atau yang disebut "dataran tinggi cinta" (dalam model Rinaldi, 1988), dengan deskripsi perilaku melalui nilai eigen (2)




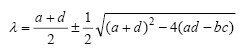
Fokus Forking Saddle
Fig. 1. Situasi dinamis dekat titik kesetimbangan dalam ruang dua dimensi, menurut persamaan 1.

Segitiga cinta

Model yang lebih kaya secara matematis diperoleh ketika orang ketiga ditambahkan ke model sederhana, khususnya karena ada kemungkinan bahwa aliansi dapat terbentuk di mana dua individu dapat bersatu melawan yang ketiga. Misalkan Romeo memiliki kekasih lain, Genevieve, meskipun orang ketiga yang dimaksud mungkin seorang anak atau kerabat lainnya. Dalam hal ini, ruang keadaan menjadi lebih mungkin enam dimensi daripada dua dimensi, karena masing-masing dari tiga memiliki perasaan untuk dua lainnya, dan dua belas parameter muncul jika masing-masing dapat mengambil gaya yang berbeda dalam kaitannya dengan yang lain, bahkan jika daya tarik alam diabaikan, ( diulas oleh Rinaldi, 1998a).

Dalam kasus yang paling sederhana, Juliet dan Genevieve mungkin tidak tahu tentang keberadaan satu sama lain, dan Romeo mungkin menunjukkan gaya romantis yang sama dalam hubungannya dengan keduanya. Sistem empat dimensi yang dihasilkan kemudian diubah menjadi dua sistem dua dimensi yang terbagi, sampai perasaan Romeo untuk Juliet entah bagaimana dipengaruhi oleh perasaan Genevieve untuknya, dan hal yang sama berlaku untuk Genevieve.

Efek nonlinear

Ada banyak cara untuk memasukkan efek non-linear. Bayangkan Romeo merespons positif cinta Juliet, tetapi dengan manifestasi cintanya yang berlebihan, ia merasa seolah dicekik dan menunjukkan reaksi yang merugikan. Sebaliknya, jika Juliet menunjukkan ketidaksukaan yang cukup, Romeo dapat mencoba menjadi menyenangkan baginya.

Dalam kasus ini, dimungkinkan untuk mengganti bJ dalam persamaan 1 dengan fungsi logistik bJ (1 - | J |) yang sesuai dengan pengukuran J dalam satuan dari kondisi bahwa J = 1 sesuai dengan nilai di mana cintanya menjadi kontraproduktif. Hasil kualitatif yang serupa mengikuti dari fungsi bJ (1 - J2), yang merupakan kasus yang dipertimbangkan oleh Rinaldi (1998b) untuk model cinta penyair Italia Platonis abad ke-14 untuk Laura yang cantik, terikat oleh perkawinan. Dengan asumsi yang sama untuk Juliet, kita mendapatkan:
(4)



Ada 4 keadaan keseimbangan, termasuk satu di titik asal. Gambar 3 menunjukkan fokus yang stabil di mana Juliet. sebagai "hasrat yang penuh hasrat" (c = d = 1) mengarahkan "pertapa" Romeo (a = b = –2) ke keadaan saling mencintai di R = J = 2. Model serupa untuk pecinta yang berhati-hati (dapat diandalkan) dengan nonlinearitas sigmoidal juga mengarah pada keseimbangan stabil (Rinaldi dan Gragnani 1998). Persamaan 4 jelas tidak memungkinkan siklus batas, dan kekacauan tidak terjadi ketika sistem dua dimensi.


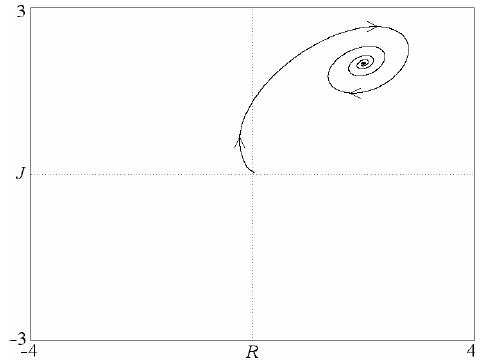Fig. 3. Salah satu solusi untuk model nonlinear menurut persamaan 4.

Mungkin penerapan efek nonlinear pada segitiga cinta.

Kata penutup

Beberapa model cinta linear yang dinamis menunjukkan dinamika yang sangat kompleks, sementara banyak dari mereka tampaknya mirip dengan pengalaman yang diketahui dalam hubungan. Jika ada tiga atau lebih variabel dan bahkan efek nonlinier paling sederhana diperkenalkan, kekacauan dapat terjadi. Perluasan model yang menarik dapat dibayangkan ketika mempertimbangkan sekelompok kepribadian yang berinteraksi, misalnya, untuk kasus keluarga besar atau komune. Model seperti itu, tentu saja, sangat disederhanakan, karena cinta diperhitungkan sebagai variabel skalar sederhana, dan reaksi individu sehubungan dengan cinta mereka sendiri dan cinta kepribadian lain bagi mereka konsisten dan mekanistik, tanpa memperhitungkan faktor pengaruh eksternal.

Cinta PS dapat hidup tanpa matematika, tetapi matematika membangkitkan cinta diri untuk orang yang menghargai harmoni sejati.

Referensi:
Julien Clinton Sprott. Model cinta yang dinamis. Psikologi dan Ilmu Hayati Dinamika Nonlinier • Agustus 2004

Rinaldi, S. (1998a). Cinta dinamika: kasus pasangan linier. Matematika dan Komputasi Terapan, 95, 181-192.
Rinaldi, S. & Gragnani, A. (1998). Cinta dinamika antara individu yang aman: Pendekatan pemodelan. Dinamika Nonlinier, Psikologi, dan Ilmu Hayati, 2, 283-301.
Rinaldi, S. (1998b). Laura dan Petrarch: Kasus yang menarik dari dinamika cinta siklus. Jurnal SIAM tentang Matematika Terapan, 58, 1205-1221