Inferensi Variasi - apa itu dan apa yang dimakannya?

Halo, Habr!

Baru-baru ini saya berbicara dengan para kolega tentang sebuah auto-encoder variasional dan ternyata banyak dari mereka yang bekerja di Deep Learning mengetahui tentang inferensi variasional (Variational Inference) dan, khususnya, batas variasional bawah hanya dengan desas-desus dan tidak sepenuhnya memahami apa itu.
Pada artikel ini saya ingin menganalisis masalah ini secara rinci. Siapa peduli, saya minta dipotong - itu akan sangat menarik.

Apa inferensi variasional?

Keluarga metode variasional pembelajaran mesin mendapat namanya dari bagian analisis matematika "kalkulus variasional". Pada bagian ini, kami mempelajari masalah mencari ekstrema fungsional (fungsional adalah fungsi fungsi - yaitu, kami tidak mencari nilai variabel di mana fungsi mencapai maksimum (minimum), tetapi fungsi di mana fungsional mencapai maksimum (minimum).

Tetapi muncul pertanyaan - dalam pembelajaran mesin, kami selalu mencari titik dalam ruang parameter (variabel) di mana fungsi kerugian memiliki nilai minimum. Artinya, itu adalah tugas analisis matematika klasik, dan di sini adalah kalkulus variasi? Kalkulus variasi muncul pada saat kita mengubah fungsi kerugian menjadi fungsi kerugian lain (seringkali ini adalah batas variasional yang lebih rendah) menggunakan metode kalkulus variasi.

Mengapa kita membutuhkan ini? Apakah tidak mungkin untuk langsung mengoptimalkan fungsi kerugian? Kita memerlukan metode ini ketika tidak mungkin untuk secara langsung mendapatkan estimasi gradien yang tidak bias (atau estimasi ini memiliki dispersi yang sangat tinggi). Sebagai contoh, set model kami $$$p (z)$dan $$$p (x / z)$, dan kita perlu menghitung $$$p (x) = \ int (p (z) p (x / z) dz)$. Inilah yang dirancang khusus untuk pembuat enkode variasional.

Apa yang dimaksud dengan Batas Bawah Variasional?

Bayangkan kita memiliki fungsi $$$f (x)$. Batas bawah pada fungsi ini adalah fungsi apa saja $$$g (x)$memenuhi persamaan:

$$

$$g (x) <= f (x)$$

Artinya, untuk fungsi apa pun ada batas bawah yang tak terhitung banyaknya. Apakah semua batas bawah ini sama? Tentu saja tidak. Kami memperkenalkan konsep lain - perbedaan (saya tidak menemukan istilah yang mapan dalam literatur berbahasa Rusia, nilai ini disebut sesak dalam artikel berbahasa Inggris):

$$

$$\ delta = maks {f (x)} - maks {g (x)}$$

Cukup jelas, residu selalu positif. Semakin kecil residual, semakin baik.

Berikut adalah contoh batas bawah dengan nol residual:

Dan ini adalah contoh dengan residu kecil tapi positif:

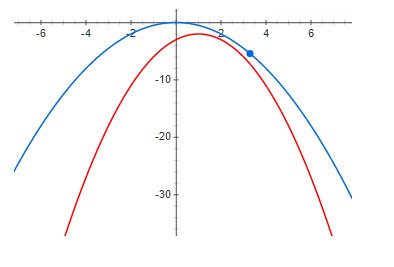
Dan akhirnya, perbedaan yang cukup besar:


Dapat dilihat dengan jelas dari grafik di atas bahwa, pada nol residual, maksimum fungsi dan maksimum batas bawah berada pada titik yang sama. Artinya, jika kita ingin menemukan maksimum beberapa fungsi, kita dapat mencari maksimum batas bawah. Jika perbedaannya tidak nol, maka ini tidak benar. Dan maksimum dari batas bawah bisa sangat jauh (sepanjang sumbu x) dari maksimum yang diinginkan. Grafik menunjukkan bahwa semakin besar residu, semakin jauh tinggi dari satu sama lain. Ini umumnya tidak benar, tetapi dalam kebanyakan kasus, intuisi ini bekerja dengan sangat baik.

Encoder Otomatis Variabel

Sekarang kita akan menganalisis contoh batas variasional rendah yang sangat baik dengan potensi nol residual (di bawahnya akan menjadi jelas mengapa) - ini adalah Autoencoder Variasional.

Tugas kita adalah membangun model generatif dan melatihnya menggunakan metode kemungkinan maksimum. Model akan memiliki bentuk berikut:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

dimana $$$q (x)$Apakah kepadatan probabilitas sampel yang dihasilkan, $$$z$- variabel laten, $$$q (z)$- kepadatan probabilitas dari variabel laten (seringkali yang sederhana - misalnya, distribusi Gaussian multidimensi dengan nol harapan dan dispersi satuan - secara umum, sesuatu yang dapat dengan mudah diambil dari sampel), $$$q_ \ theta (x | z)$- Kepadatan sampel bersyarat untuk nilai tertentu dari variabel laten, dalam autoencoder variasional, yang Gaussian dengan harapan dan dispersi mat tergantung pada z yang dipilih.

Mengapa kita perlu merepresentasikan kepadatan data sedemikian rumitnya? Jawabannya sederhana - data memiliki fungsi kerapatan yang sangat kompleks dan kami tidak bisa secara teknis membangun model kerapatan tersebut secara langsung. Kami berharap bahwa kerapatan kompleks ini dapat diperkirakan dengan baik menggunakan dua kerapatan yang lebih sederhana. $$$q (z)$dan $$$q_ \ theta (x | z)$.

Kami ingin memaksimalkan fungsi berikut:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

dimana $$$p (x)$- kepadatan probabilitas data. Masalah utama adalah kepadatannya $$$q (x)$(dengan model yang cukup fleksibel) tidak mungkin untuk disajikan secara analitis, dan sesuai dengan itu untuk melatih model.

Kami menggunakan rumus Bayes dan menulis ulang fungsi kami sebagai berikut:

$$

$$I = \ int {p (x) log (\ frac {q (z) q (x | z)} {q (z | x)}) dx}$$

Sayangnya $$$q (z / x)$semuanya juga sulit untuk dihitung (tidak mungkin untuk mengambil integral secara analitis). Tetapi pertama-tama, kita perhatikan bahwa ekspresi di bawah logaritma tidak bergantung pada z, jadi kita dapat mengambil ekspektasi matematis dari logaritma dalam z dari distribusi apa pun dan ini tidak akan mengubah nilai fungsi dan mengalikan dan membaginya dengan logaritma menjadi distribusi yang sama (secara formal kita hanya memiliki satu syarat) - distribusi ini seharusnya tidak hilang di mana saja). Sebagai hasilnya, kita mendapatkan:

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + Log \ int {p (x) dx \ int {\ phi (z | x) (\ frac {\ phi (z | x)} {q (z | x)})}}$$

perhatikan bahwa, pertama, istilah kedua adalah KL divergence (yang berarti selalu positif):

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) KL [\ phi (z | x) || q (z | x))] dx}$$

dan kedua $$$I$tidak bergantung pada $$$q (z | x)$bukan dari $$$\ phi (z | x)$. Oleh karena itu,

$$

$$I> = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} = VLB$$

dimana $$$Vlb$- Batas variasional yang lebih rendah (Variational Lower Bound) dan mencapai maksimum ketika $$$KL [\ phi (z | x) || q (z | x))] = 0$- yaitu distribusinya sama.

Positivitas dan kesetaraan menjadi nol jika dan hanya jika distribusi bertepatan KL-divergensi dibuktikan secara tepat dengan metode variasional - maka nama batas variasional.

Saya ingin mencatat bahwa penggunaan batas bawah variasional memberikan beberapa keuntungan. Pertama, ini memberi kita kesempatan untuk mengoptimalkan fungsi kerugian dengan metode gradien (coba lakukan ini ketika integral tidak diambil secara analitik) dan kedua, ia mendekati distribusi terbalik $$$q (z | x)$distribusi $$$\ phi (z | x)$- yaitu, kita tidak bisa hanya sampel data, tetapi juga sampel variabel laten. Sayangnya, kelemahan utama adalah ketika model distribusi terbalik tidak fleksibel, yaitu ketika keluarga $$$\ phi (z | x)$tidak mengandung $$$q (z | x)$- residunya akan positif dan sama:

$$

$$\ delta = \ int {p (x) \ underset {\ phi (z | x)} {min} (KL [\ phi (z | x) || q (z | x)]) dx}$$

yang berarti bahwa maksimum batas bawah dan fungsi kerugian kemungkinan besar tidak bersamaan. Omong-omong, variational auto encoder yang digunakan untuk menghasilkan gambar menghasilkan gambar yang terlalu buram, saya pikir ini hanya karena memilih keluarga yang terlalu miskin $$$\ phi (z | x)$.

Contoh garis bawah yang tidak begitu baik

Sekarang kita akan mempertimbangkan contoh di mana, di satu sisi, batas bawah memiliki semua sifat yang baik (dengan model yang cukup fleksibel, residual akan menjadi nol), tetapi pada gilirannya tidak memberikan keuntungan apa pun jika menggunakan fungsi kerugian semula. Saya percaya bahwa contoh ini sangat terbuka dan jika Anda tidak melakukan analisis teoretis, Anda dapat menghabiskan banyak waktu untuk melatih model yang tidak masuk akal. Sebaliknya, model masuk akal, tetapi jika kita dapat melatih model seperti itu, maka lebih mudah untuk memilih $$$q (x)$dari keluarga yang sama dan gunakan prinsip kemungkinan maksimum secara langsung.

Jadi, kami akan mempertimbangkan model generatif yang sama persis seperti pada kasus encoder otomatis variasional:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

kami akan berlatih dengan metode kemungkinan maksimum yang sama:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

Kami masih berharap itu $$$q (x | z)$Ini akan jauh lebih "mudah" daripada $$$q (x)$.
Hanya sekarang kita akan menulis $$$I$sedikit berbeda:

$$

$$I = \ int {p (x) log (\ int {q (z) q_ \ theta (x | z) dz}) dx}$$

menggunakan rumus Jensen, kita mendapatkan:

$$

$$I> = \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz} = VLB$$

Justru pada saat inilah kebanyakan orang merespons tanpa berpikir bahwa ini benar-benar garis bawah dan Anda dapat melatih model. Ini benar, tetapi mari kita lihat perbedaannya:

$$

$$\ delta = \ int {p (x) log (q (x)) dx} - \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz}$$

dimana (dengan menerapkan formula Bayes dua kali):

$$

$$$ delta = \ int {p (x) q (z) log (\ frac {q (x)} {q (x | z)}) dxdz} = \ int {p (x) q (z) log ( \ frac {q (z)} {q (z | x)}) dxdz}$$

mudah untuk melihat bahwa:

$$

$$\ delta = \ int {p (x) KL [q (z) || q (z | x)] dx}$$

Mari kita lihat apa yang terjadi jika kita menambah batas bawah - residunya akan berkurang. Dengan model yang cukup fleksibel:

$$

$$KL [q (z) || q (z | x)] \ rightarrow0$$

semuanya tampak baik-baik saja - batas bawah memiliki potensi nol residual dan dengan model yang cukup fleksibel $$$q (x | z)$semuanya harus bekerja. Ya, ini benar, hanya pembaca yang penuh perhatian yang dapat melihat bahwa nol residual tercapai saat $$$x$dan $$$z$adalah variabel acak independen !!! dan untuk hasil yang baik, “kompleksitas” distribusi $$$q (x | z)$seharusnya tidak kurang dari $$$q (x)$. Artinya, batas bawah tidak memberi kita keuntungan.

Kesimpulan

Batas variasional yang lebih rendah adalah alat matematika yang sangat baik yang memungkinkan Anda untuk sekitar mengoptimalkan fungsi "tidak nyaman" untuk belajar. Tetapi seperti alat lainnya, Anda harus sangat memahami kelebihan dan kekurangannya dan juga menggunakannya dengan sangat hati-hati. Kami menganggap contoh yang sangat baik - auto-encoder variasional, serta contoh batas bawah yang tidak terlalu baik, sementara masalah batas bawah ini sulit dilihat tanpa analisis matematis terperinci.

Saya harap itu setidaknya sedikit bermanfaat dan menarik.