🚽 🛬 👠 Formula untuk menghitung bilangan prima dan mengoptimalkan pembagi brute force 💟 🛶 🔟

Salam! Saya memutuskan pada waktu luang saya untuk meneliti masalah menemukan bilangan prima. Topiknya luas dan menarik. Saya ingin berbagi beberapa pemikiran tentang hal itu yang terlintas di benak saya. Pencarian di Internet tidak mengungkapkan hal itu, menunjukkan keasliannya.

Pertama, saya belum pernah menemukan rumus matematika untuk menghitung bilangan prima secara berurutan. Tetapi bagaimanapun juga, jika ada algoritma, maka dimungkinkan untuk membuat formula menggunakan fungsi logis atau operator. Saya berikan di bawah ini rumus paling ringkas yang ternyata.

Untuk beberapa urutan angka

(x_{m}) = x_{1}, x_{2}, x_{3}, . . . x_{m a x}

$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ kami memperkenalkan operator deteksi nomor pertama sama dengan:

\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {jika} \ \ ada \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {dan} \ x_ {m} = a \\ 0 \ \ mathbf {jika tidak} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ benar.

$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {jika} \ \ ada \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {dan} \ x_ {m} = a \\ 0 \ \ mathbf {jika tidak} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ benar.$

Semua bilangan prima, dimulai dengan 5, dapat dihitung dengan rumus:

P_{n} = P_{n - 1} + 2 m a t h b f D t_{0}^{i} (m a t h b f D t_{0}^{j} ((P_{n - 1} + 2 i) m o d P_{j + 1})), f o r a l l n g e q s l a n t 3 f o r a l l i_{m a x} g e q s l a n t m a x f r a c P_{a l p h a} - P_{a l p h a - 1} 2 + 10,, 2 l e q s l a n t a l p h a l e q s l a n t n - 1; j_{m a x} = p i (s q r t P_{n - 1} + 2 i) - 1

$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$

Operator

m a t h b f D t_{0}^{j}

$\ mathbf {Dt_ {0} ^ {j}}$ beralih lagi

j

$j$ sisanya membagi masing-masing nomor kandidat dengan kesederhanaan dengan

i

$i$ angka

(P_{n - 1} + 2 i)

$(P_ {n-1} + 2i)$ untuk bilangan prima sudah ditemukan dalam kisaran hingga

P_{j_{m a x} + 1}

$P_ {j_ {max} +1}$ . Nomor kandidat dipilih secara berurutan dari himpunan bilangan ganjil yang lebih besar dari bilangan prima sebelumnya

P_{n - 1}

$P_ {n-1}$ .

p i (s q r t P_{n - 1} + 2 i)

$\ pi (\ sqrt {P_ {n-1} + 2i})$ Merupakan fungsi pi yang menunjukkan jumlah bilangan prima

l e q s l a n t s q r t P_{n - 1} + 2 i

$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
Operator

m a t h b f D t_{0}^{i}

$\ mathbf {Dt_ {0} ^ {i}}$ beralih lagi

i

$i$ nilai output operator

m a t h b f D t_{0}^{j}

$\ mathbf {Dt_ {0} ^ {j}}$ sampai ditemukan 0. Karena rangkaian bilangan prima tak terbatas, ini akan terjadi cepat atau lambat. Di pintu keluar operator

m a t h b f D t_{0}^{i}

$\ mathbf {Dt_ {0} ^ {i}}$ jadi akan selalu ada beberapa nomor

i

$i$ . Batas bawah

i_{m a k s}

$i_ {maks}$ ditentukan oleh perbedaan maksimum bilangan prima yang berdekatan lebih kecil dari yang diinginkan. Peningkatan perbedaan ini terjadi secara logaritmik. Grafik di bawah ini menunjukkan ketergantungan pertumbuhan maksimum dan rata-rata

D e l t a P_{a l p h a}

$\ Delta P _ {\ alpha}$ dari n untuk 100.000 bilangan prima pertama. Nilai maksimum disampel dan dirata-rata untuk setiap seribu angka. gambar

Peningkatan maksimum dalam perbedaan bilangan prima

d e l t a_{m a x} (D e l t a P_{a l p h a})

$\ delta _ {max} (\ Delta P _ {\ alpha})$ ke nilai maksimum sebelumnya

m a x (D e l t a P_{a l p h a})

$max (\ Delta P _ {\ alpha})$ sama dengan 20 (untuk perbedaan bilangan prima 31397-31469 = 72 sehubungan dengan perbedaan 25523-25471 = 52). Itu adalah di wilayah di mana turunan dari logaritma amplop

D e l t a P_{a l p h a}

$\ Delta P _ {\ alpha}$ masih cukup besar, dan bilangan prima tidak lagi terlalu kecil. Berdasarkan nilai ini, kondisi untuk

i_{m a k s}

$i_ {maks}$ . Grafik

d e l t a_{m a x} (D e l t a P_{a l p h a})

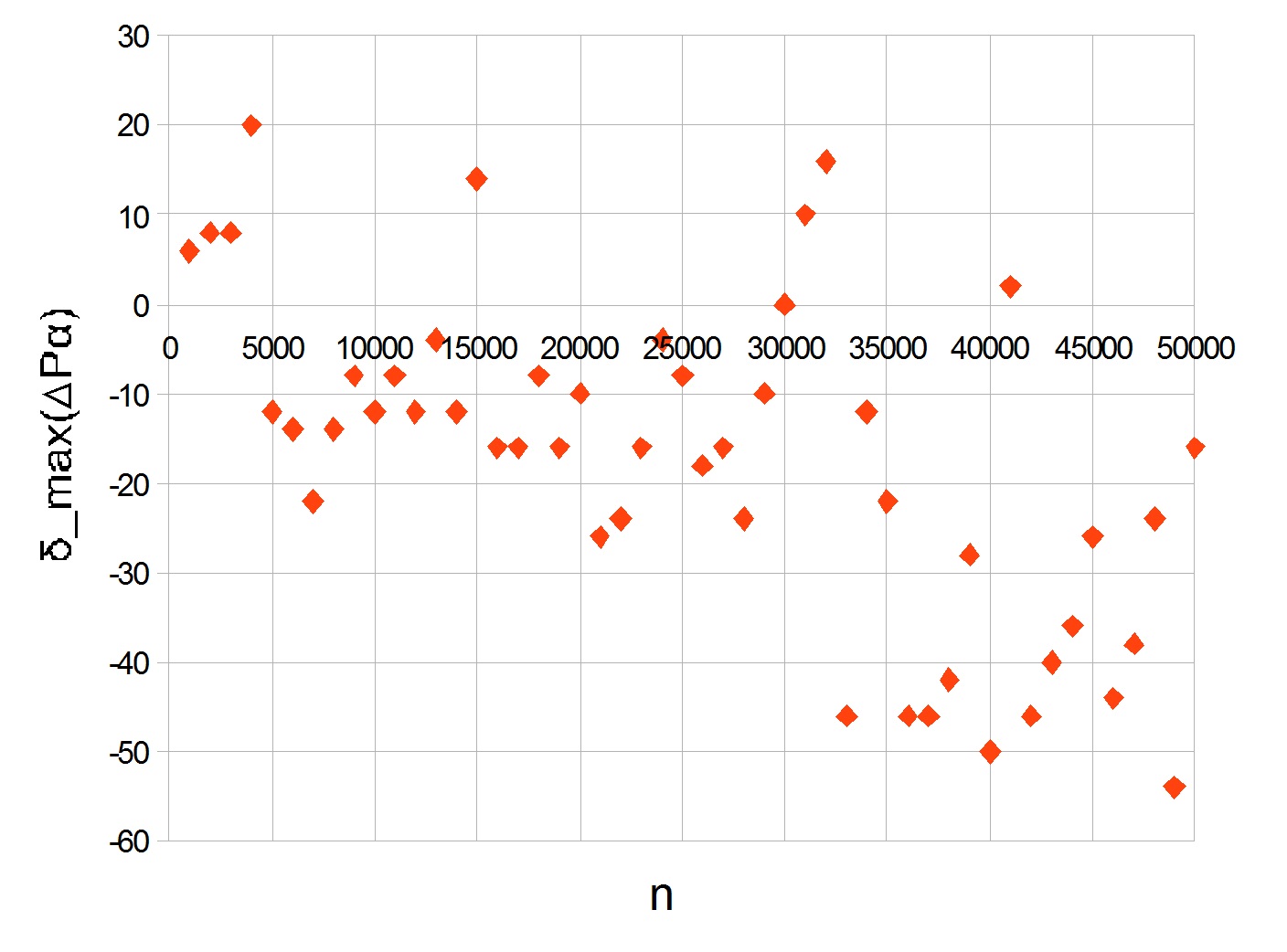
$\ delta _ {max} (\ Delta P _ {\ alpha})$ untuk 50.000 bilangan prima pertama yang diberikan di bawah ini. Nilai dihitung untuk setiap seribu. gambar

Puncaknya terlihat pada 20. Dengan meningkatnya n, grafik menjadi minus, menunjukkan penurunan tingkat pertumbuhan bilangan prima besar.

Pertimbangan kedua adalah mengoptimalkan perhitungan urutan bilangan prima.
Algoritma yang ditetapkan dalam rumus di atas adalah metode yang ditingkatkan untuk menghitung pembagi. Perbaikan adalah untuk mengecualikan angka genap dari pertimbangan dan memeriksa pembagian hanya bilangan prima lebih kecil dari sq. akar nomor kandidat. Bagian tersulit dari algoritma adalah perhitungan dari himpunan fungsi mod yang tersisa. Kompleksitas dapat dikurangi dengan mengoptimalkan fungsi ini. Namun, ada cara yang bahkan lebih efektif. Biarkan

(r_{j + 1}^{n - 1}) = r_{2}, r_{3}, . . . r_{p i (s q r t P_{n - 1})}

$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ Adalah urutan residu dari membagi bilangan prima yang ditemukan terakhir menjadi bilangan prima dari 3 ke akar. Kami akan membuat urutan formulir

(r_{i, j + 1}^{n}) = (r_{2} + 2 i) m o d P_{2}, (r_{3} + 2 i) m o d P_{3}, . . . (r_{p i (s q r t P_{n - 1})} + 2 i) m o d P_{p i (s q r t P_{n - 1})}, (P_{n - 1} + 2 i) m o d P_{p i (s q r t P_{n - 1} + 2 i)}

$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$

dalam urutan mulai dari

i = 1

$i = 1$ . Istilah terakhir dihitung jika

p i (s q r t P_{n - 1} + 2 i) n e q p i (s q r t P_{n - 1})

$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . Ketika pada beberapa langkah perhitungan sisanya

r_{i, j + 1}^{n}

$r_ {i, j + 1} ^ {n}$ menjadi sama dengan 0, pergi ke urutan berikutnya. Ini dilakukan sampai saya ditemukan, di mana semua residu bukan nol. Ini berarti menemukan bilangan prima berikutnya. Urutan

(r_{j + 1}^{n})

$(r_ {j + 1} ^ {n})$ itu harus disimpan sampai bilangan prima berikutnya ditemukan. Rumus berulang untuk menghitung bilangan prima dengan cara ini dikonversi menjadi:

P_{n} = P_{n - 1} + 2 m a t h b f D t_{0}^{i} (m a t h b f D t_{0}^{j} (r_{i, j + 1}^{n})), f o r a l l n g e q s l a n t 3

$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1} ^ { n})), \ \ \ \ forall \, n \ geqslant 3$

Dalam algoritma yang disajikan, mod operasi difasilitasi: habis dibagi oleh

(r_{j + 1} + 2 i) / P_{j + 1}

$(r_ {j + 1} + 2i) / P_ {j + 1}$ kali lebih banyak pembagi. Satu-satunya pengecualian adalah terjadinya pembagi sederhana yang baru. Dalam memori komputer, ketika mengimplementasikan algoritma, perlu untuk menyimpan array bilangan prima ke root yang dicari, serta array variabel residual. Kompleksitas algoritma dalam pengertian umum (jumlah pekerjaan) mungkin kurang dari metode yang dikenal lainnya. Operasi paling kompleks di dalamnya adalah ekstraksi akar kuadrat, perhitungan residu dan penggandaan. Root dapat diekstraksi ke integer terdekat. Untuk mendapatkan residu, Anda dapat menggunakan algoritme yang efektif berdasarkan aturan umum pembagian. Perkalian hanya digunakan oleh 2 angka yang relatif kecil i . Kompleksitas waktu dari algoritma dapat dikurangi dengan mendistribusikan pekerjaan sesuai dengan nilai-nilai i . Saringan tersegmentasi yang diperoleh dengan cara ini harus bekerja lebih cepat pada komputer multi-utas. Namun, pekerjaan yang dilakukan akan lebih besar karena peningkatan dividen. Anda juga dapat "mengacaukan" faktorisasi roda ke algoritme. Dengan ukuran roda yang optimal, ini dapat mengurangi kerumitan dalam kisaran n - hingga perangkat keras "liar" memperlambatnya.

Mungkin seseorang akan berguna pikiran saya.

Formula untuk menghitung bilangan prima dan mengoptimalkan pembagi brute force

More articles: