Stochastic gradient descent (SGD) untuk fungsi kehilangan logaritmik (LogLoss) dalam masalah klasifikasi biner

Bagian sebelumnya (tentang regresi linier, gradient descent, dan cara kerjanya) - habr.com/en/post/471458

Pada artikel ini, saya akan menunjukkan solusi untuk masalah klasifikasi pertama, seperti yang mereka katakan, "pena", tanpa perpustakaan pihak ketiga untuk SGD, LogLoss dan menghitung gradien, dan kemudian menggunakan perpustakaan PyTorch.

Tujuan: untuk dua fitur kategorikal yang menggambarkan kekuningan dan simetri, tentukan kelas mana (apel atau pir) yang dimiliki objek (ajarkan model untuk mengklasifikasikan objek).

Untuk memulai, unggah dataset kami:

import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10) 

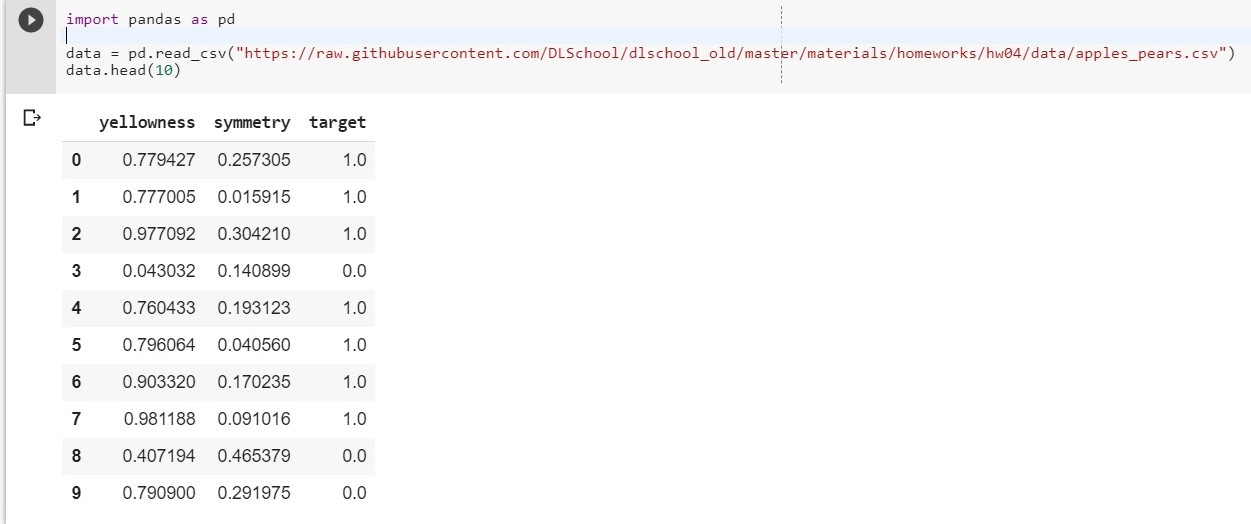
Biarkan: x1 - kekuningan, x2 - simetri, y = lebih besar

Kami menyusun fungsi y = w1 * x1 + w2 * x2 + w0
(w0 akan dianggap bias (eng. - bias))

Sekarang tugas kita direduksi menjadi menemukan bobot w1, w2, dan w0, yang paling akurat menggambarkan ketergantungan y pada x1 dan x2.

Kami menggunakan fungsi kehilangan logaritmik:



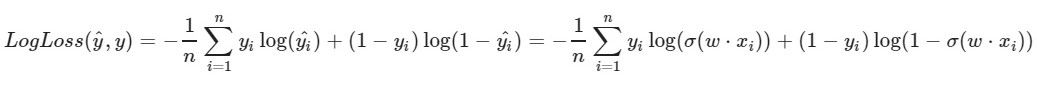
Parameter kiri dari fungsi adalah prediksi dengan bobot saat ini w1, w2, w0

Parameter yang benar dari fungsi adalah nilai yang benar (kelas adalah 0 atau 1)

σ (x) adalah fungsi aktivasi sigmoid dari x

log (x) - logaritma natural x

Jelas bahwa semakin kecil nilai fungsi kerugian, semakin baik kita memilih bobot w1, w2, w0. Untuk melakukan ini, pilih keturunan gradien stokastik .

Saya perhatikan bahwa rumus untuk LogLoss akan mengambil pandangan yang berbeda mengingat fakta bahwa dalam SGD kita memilih satu elemen dan bukan seluruh pilihan (atau subsampel, seperti dalam kasus penurunan gradien mini-batch):


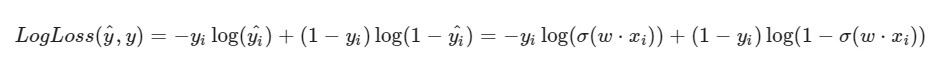Kemajuan solusi:

Bobot awal w1, w2, w0 diberi nilai acak

Kami mengambil objek ke-i tertentu dari dataset kami (misalnya, acak), menghitung LogLoss untuknya (dengan w1, w2, dan w0, yang awalnya kami berikan nilai acaknya), kemudian kami menghitung turunan parsial untuk masing-masing bobot w1, w2 dan w0, kemudian perbarui masing-masing bobot.

Sedikit persiapan:

 import pandas as pd import numpy as np X = data.iloc[:,:2].values #  - y = data['target'].values.reshape((-1, 1)) #  (    ) x1 = X[:, 0] x2 = X[:, 1] def sigmoid(x): return 1 / (1 + np.exp(-x)) 

Implementasi:

 import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0) # form range 0..999 idx = np.arange(1000) # random shuffling np.random.shuffle(idx) x1, x2, y = x1[idx], x2[idx], y[idx] # learning rate lr = 0.001 # number of epochs n_epochs = 10000 for epoch in range(n_epochs): i = random.randint(0, 999) yhat = w1 * x1[i] + w2 * x2[i] + w0 w1_grad = -((y[i] - sigmoid(yhat)) * x1[i]) w2_grad = -((y[i] - sigmoid(yhat)) * x2[i]) w0_grad = -(y[i] - sigmoid(yhat)) w1 -= lr * w1_grad w2 -= lr * w2_grad w0 -= lr * w0_grad print(w1, w2, w0) 

[0.49671415] [-0.1382643] [0.64768854]
[0.87991625] [-1.14098372] [0.22355905]

* _grad adalah turunan dari bobot yang sesuai. Saya akan menulis formula umum:



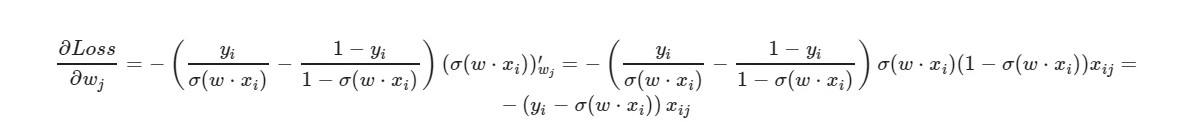
Untuk istilah bebas w0 - faktor x dihilangkan (diambil sama dengan satu).

Dengan menggunakan rumus akhir derivatif, kita dapat melihat bahwa kita tidak perlu menghitung fungsi kerugian secara eksplisit (kita hanya perlu derivatif parsial).

Mari kita periksa berapa banyak objek dari set pelatihan model kita memberikan jawaban yang benar, dan berapa banyak - yang salah.

 i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect) 

925 75

np.around (x) - membulatkan nilai x. Bagi kami: jika x> 0,5, maka nilainya adalah 1. Jika x ≤ 0,5, maka nilainya adalah 0.

Dan apa yang akan kita lakukan jika jumlah fitur objek adalah 5? 10? 100? Dan kita akan memiliki jumlah bobot yang sesuai (ditambah satu untuk bias). Jelas bahwa secara manual bekerja dengan setiap bobot, menghitung gradien untuk itu tidak nyaman.

Kami akan menggunakan pustaka PyTorch yang populer.

PyTorch = NumPy + CUDA + Autograd (perhitungan gradien otomatis)

Implementasi PyTorch:

 import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss) 

OrderedDict ([('0,weight', tensor ([[- 0,4148, -0,5838]]))), ('0.bias', tensor ([0,5448])]]))
OrderedDict ([('0.weight', tensor ([[5.4915, -8.2156]]))), ('0.bias', tensor ([- 1.1130])]]))
0,03930133953690529

Kerugian yang cukup baik pada sampel uji.

Di sini, MSELoss dipilih sebagai fungsi kerugian.

Lebih lanjut tentang Linear

Singkatnya: kita memberikan 2 parameter ke input (x1 dan x2 kita seperti dalam contoh sebelumnya) dan kita mendapatkan satu parameter (y) untuk output, yang, pada gilirannya, diumpankan ke input fungsi aktivasi. Dan kemudian mereka sudah dihitung: nilai fungsi kesalahan, gradien. Pada akhirnya - bobot diperbarui.

Bahan yang digunakan dalam artikel