Segala Sesuatu yang Ingin Anda Ketahui tentang Pendulum Mundur

Artikel ini berfungsi sebagai lembar contekan bagi mereka yang ingin membuat bandul terbalik. Berikut adalah masalah-masalah yang saya ulang beberapa kali, tinjauan singkat teori diperlukan untuk memahami bagaimana menstabilkan sistem.

Mengapa saya membutuhkan ini?

Singkatnya: Saya ingin memperluas mesin CNC saya, tetapi ada yang tidak beres ...

Usaha yang gagal

Proyek ini memakan waktu hampir dua tahun trial and error, mendesain ulang, menunggu detail dan hari libur yang tidak lengkap, sehingga mereka yang ingin mengulangi menghemat waktu dan kegelisahan mereka, saya menganggap perlu untuk berbicara tentang keputusan yang gagal.

• sebuah giroskop (MPU6050) bukan encoder - pada dasarnya tidak ada yang menentangnya, tetapi sensor harus ditempatkan pada batang yang berputar, ini memperkenalkan efek yang tidak terduga dan ketidakmampuan untuk menggulir batang beberapa kali di sekitar sumbu.
  
• encoder absolut - jika ini merupakan potensiometer, bahkan pergerakan kabel (terutama karena kontak di Arduino) memasukkan noise ke dalam pengukuran, ADC 10-bit masih belum cukup; jika ini merupakan sensor yang lebih mahal, maka pembacaan dilakukan melalui antarmuka serial, dan ini menyebabkan penundaan pada sistem, terutama dalam kombinasi dengan motor stepper.
  
• kekakuan sistem - pada titik tertentu saya mengambil tabung aluminium dengan beban di ujungnya, ketika kereta bergetar, getaran kuat dimulai di dalamnya, dan tidak segera jelas sistem mana yang kami stabilkan. Kita harus berusaha untuk memastikan bahwa sistem fisik sedekat mungkin dengan apa yang dimodelkan.
  
• gesekan - fenomena ini sering diabaikan, saya mencoba menguranginya menggunakan roda kereta besar dan profil V-slot, berbeda dengan rel dengan slider dengan bola kecil, karena gesekan bergulir berbanding terbalik dengan jari-jari.
  
• penggunaan motor stepper - Saya menghabiskan banyak waktu untuk mencoba rute ini, itu menyesatkan untuk menyederhanakan formula (pada kenyataannya, kami segera mengontrol percepatan pangkal pendulum) dan kesederhanaan desain (kita bisa melupakan gesekan pada rel, motor encoder, jika kita mengasumsikan bahwa motor tidak melewati langkah) , tapi ... Untuk mengontrol kecepatan secara akurat, waktu antara langkah-langkah harus puluhan mikrodetik, yang berarti Anda bisa melupakan output negara ke konsol. Tanpa umpan balik, Anda tidak dapat memastikan bahwa motor tidak ketinggalan langkah dan kecepatannya benar-benar seperti yang dipikirkan sistem. Saya tidak mengklaim bahwa ini adalah solusi buntu, jika seseorang berhasil menstabilkan pendulum dengan motor stepper, saya akan senang melihatnya.
  

Pendulum gratis

Untuk melengkapi gambar, kami mensimulasikan pendulum pada kereta gratis tanpa gesekan.

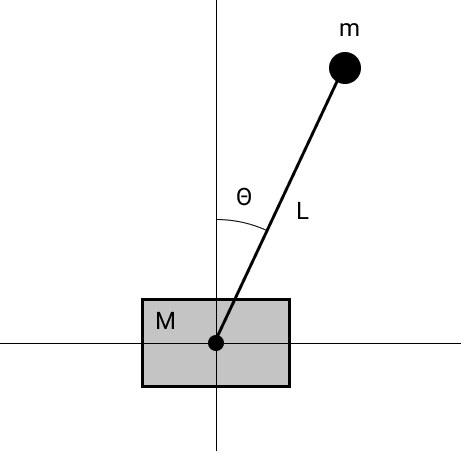
Persamaan gerak dapat diperoleh dengan membedakan Lagrangian sehubungan dengan koordinat umum. Kami memperoleh persamaan berikut:

$$

$$\ begin {cases} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta )} = 0 \ end {cases}$$

dari mana Anda dapat menemukan bagaimana perubahan vektor negara:

$$

$$\ begin {cases} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin (\ theta)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos (\ theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ titik {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin (\ theta)} - g \ cdot {sin (\ theta)} \ cdot {cos (\ theta)}} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {cases}, b = \ frac {m} {M + m}$$

dan mensimulasikan sistem. Kodenya ada di sini .

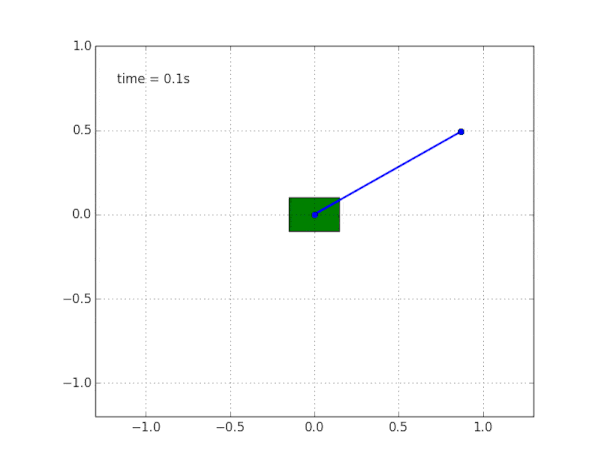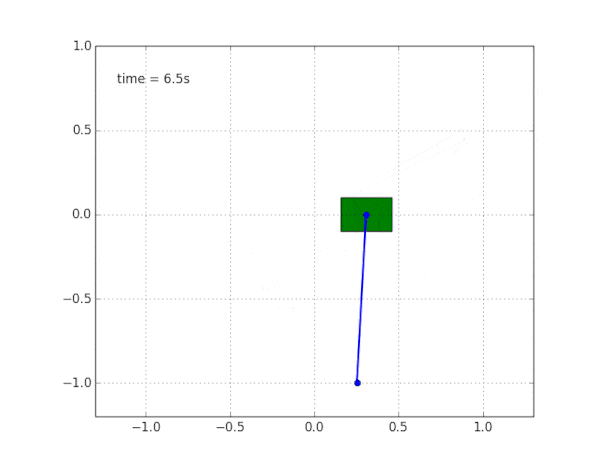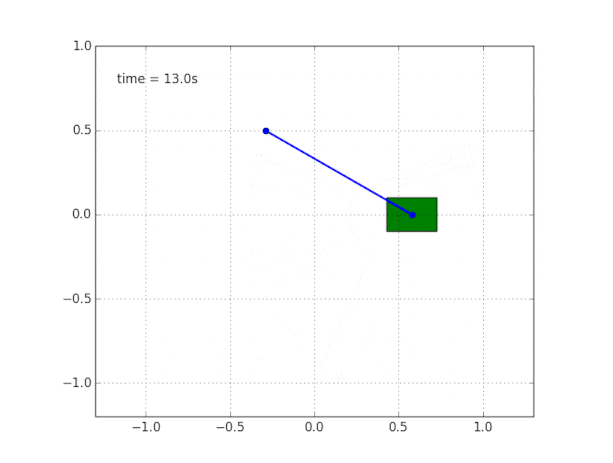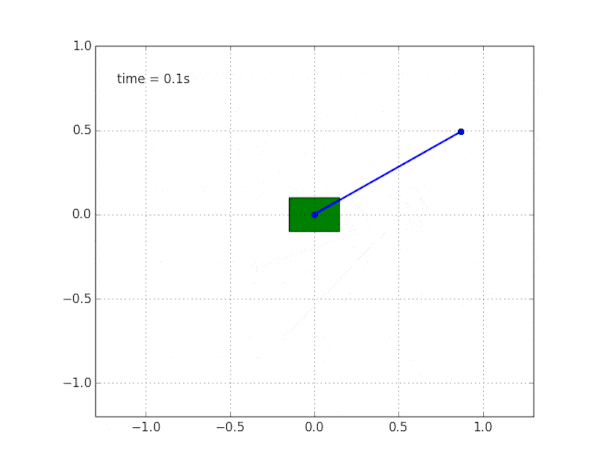
Mengapa sistem tidak stabil?

Akal sehat dan visualisasi memberi tahu kita bahwa bandul itu sendiri tidak akan berdiri. Tetapi bagaimana cara memverifikasi ini secara matematis?
Secara umum, sistem dan solusi linierisasi adalah sebagai berikut:

$$

$$\ dot {\ mathbf {x}} = A \ mathbf {x}, \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$$

Eksponen dalam kekuatan matriks terlihat lebih jelas, jika kita pergi ke sistem koordinat dari vektor eigen, maka matriks $$$A$ akan menjadi diagonal ( $$$D$ ), dan peserta pameran akan terlihat seperti:

$$

$$e ^ {Dt} = \ begin {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$$

Sekarang terlihat, di hadapan nilai eigen ( $$$\ lambda_i$ ) dengan bagian nyata positif, komponen yang sesuai dari vektor keadaan akan cenderung tak hingga, dan sistem akan berantakan. Hal di atas berlaku untuk sistem berkelanjutan, lebih lanjut tentang keberlanjutan dijelaskan dalam ceramah video ini .
Periksa apakah ini kasus untuk pendulum terbalik. Kami membuat linierisasi sistem kami di dekat posisi keseimbangan untuk $$$\ theta = 0, sin (\ theta) \ approx \ theta, cos (\ theta) \ approx 1, w ^ 2 \ approx 0$ :

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$$

Nilai eigen bukan nol memiliki formulir $$$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$ , jadi kami menjadi yakin akan ketidakstabilan.

Tambahkan umpan balik

Sekarang gaya akan bertindak pada carriage $$$f$ , salah satu persamaan dapat ditulis ulang dalam bentuk: $$$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta)} = f$ , dan sistem yang dilinearisasi akan berbentuk:

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ begin {bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}$$

Sekarang sistem ( $$$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$ ) menjadi terkendali , ini dapat diverifikasi dengan memeriksa pangkat matriks $$$\ begin {bmatrix} B&& AB&& A ^ 2B && A ^ 3B \ end {bmatrix}$ sama dengan dimensi vektor keadaan, mis. 4. Untuk menjaga pendulum dalam posisi tegak, saya menggunakan pengontrol keadaan linear-kuadratik, yaitu control (u atau f) adalah produk dari vektor keadaan $$$[\ theta, \ dot {\ theta}, x, \ dot {x}]$ oleh vektor parameter yang ditemukan sekali dengan meminimalkan fungsional kuadratik . Kode simulasi ada di sini .

Kontrol mesin

Sekarang Anda perlu mengendalikan motor DC, itu berisi banyak parameter yang saya tidak tahu, jadi saya mengambilnya untuk "kotak hitam", dijelaskan oleh persamaan berikut, dengan mempertimbangkan gesekan akun:

$$

$$\ begin {cases} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {tanda (v)} \ end {cases}$$

Anda dapat membaca tentang derivasi persamaan dan estimasi parameter di sini . Di bawah ini saya memberikan grafik percepatan motor dengan carriage tergantung pada tegangan (pada kenyataannya, sinyal PWM adalah output dari controller) dan kurva dipasang.

Saya juga menemukan koefisien model dengan brute force, kode .
Jadi, controller memberi kita akselerasi yang diperlukan, dan dari persamaan ke-2, mengetahui semua konstanta, kita menemukan voltase.

Menyatukan perangkat nyata

Sekarang kita memiliki semua pengetahuan untuk mengumpulkan dan menstabilkan pendulum. Saya menggunakan besi berikut:

• Arduino Mega 2560 bukan UNO, karena dua encoders memerlukan 4 pin untuk interupsi
• Encoder untuk pendulum - OMRON E6B2-CWZ6C 2500 pulsa per revolusi - memberi kita sudut, kita menghitung kecepatan sudut, resolusinya cukup tinggi, sehingga ada perbedaan hingga yang cukup tanpa perataan dan rata-rata
• Encoder untuk motor - LPD3806-600BM-G5-24C 600 pulsa per revolusi - memberikan posisi carriage, menghitung kecepatan
• Motor 12V DC dengan gearbox 5: 1
• Driver Motor 10Amp 5V-30V

Jadi, kami secara eksplisit mengukur sudut pendulum, posisi carriage, menghitung kecepatan sudut pendulum dan kecepatan carriage - kami mendapatkan status penuh, saya menemukan parameter pengontrol dengan skrip ini . Anehnya, semuanya berjalan dengan cepat. Saya puas dengan hasilnya, ia berdiri dan bahkan memegang gelas!


Kode untuk Arduino ada di sini
Apa yang bisa ditingkatkan dibandingkan dengan banyak opsi yang dapat ditemukan di youtube - bandul ini sepi karena PWM disetel di luar rentang pendengaran dan roda plastik digunakan.
Sekarang tugas ini terlihat seperti pekerjaan laboratorium: mengukur parameter motor dan menemukan koefisien regulator, sekaligus memahami apa yang terjadi.

Apa selanjutnya

Saya berencana untuk menghasilkan pendulum: membuat ayunan, menyingkirkan gulungan kabel, membuat perisai dengan konektor yang nyaman sehingga tidak memalukan untuk menyumbang ke beberapa sekolah atau museum. Jika seseorang ingin bergabung, saya akan senang ada banyak ide yang lebih ambisius.

Referensi

• Penjelasan rinci tentang masalah pendulum terbalik
• Kami mengunyah regulator linier-kuadratik untuk mengontrol pendulum terbalik - artikel ini menyelamatkan saya banyak waktu ketika membangun pendulum saya
• Kuliah video TAU yang luar biasa

Terima kasih atas perhatian anda!