Panduan matematika singkat untuk orang asing

Tentang apa ini?

Dan bagaimana seseorang bisa membuat bahan yang diperlukan dari program pertama universitas di sepuluh keempat dan dengan keengganan aljabar?

Untuk kegilaan pemberani kami menyanyikan lagu!

Target audiensi dari Buku Panduan ini adalah mereka yang tiba-tiba tertarik pada matematika atau merasa perlu untuk meningkatkan efektivitas profesional mereka, tetapi untuk beberapa alasan mereka tidak dapat mengabdikan beberapa tahun hidupnya untuk pendidikan akademik. Jika Anda memiliki kebutuhan untuk memahami, tetapi pengetahuan mendasar sangat kurang, dan Anda merasa seperti orang asing di negara matematika, di mana mereka berbicara bahasa yang tidak dapat dipahami, cobalah untuk pergi dengan cara ini sebagai turis. Seluruh rute adalah tur wisata dan dirancang selama beberapa hari, maksimal dua minggu. Sebagai perbandingan: kursus akademik penuh adalah sekitar lima tahun. Tujuan akhir dari rute yang diusulkan adalah untuk menjadi akrab dengan prinsip-prinsip satu bagian yang sangat khusus - kriptografi elips. Namun, tidak perlu sampai akhir jika bagian ini berada di luar lingkup minat Anda atau jika Anda dihadapkan dengan kesulitan atau bahaya serius. Tetapi, sejak Anda mengambil Panduan, masih mencoba untuk mencapai setidaknya bagian "Bahasa Formula".

Seperti kamus, panduan ini juga dapat digunakan untuk terjemahan terbalik. Mungkin akan bermanfaat bagi matematikawan yang dipaksa untuk menghubungi dan bekerja sama dengan non-matematikawan, terus-menerus mengatasi kesenjangan kesalahpahaman. Kasus ini tampaknya sangat sulit sehingga garis Maxim Gorky dalam prasasti adalah jawaban universal bagi kedua belah pihak. Bagaimanapun, saya berharap umpan balik dan mencoba untuk menambah pengetahuan kita tentang mengapa mereka tidak mengerti kita, dan bagaimana ini bisa diperbaiki.

Dan sekarang, mengetahui bahwa tidak ada jalan kerajaan di sini, kami akan mencoba membuka setidaknya satu jalur wisata.

Bahasa Formula

Saya diberi tahu bahwa setiap formula yang termasuk dalam buku akan membagi dua jumlah pelanggan. Kemudian saya memutuskan untuk melakukannya tanpa formula sama sekali. Benar, pada akhirnya saya masih menulis satu persamaan - persamaan Einstein yang terkenal E = mc ^ 2. Saya harap itu tidak menakuti setengah dari pembaca potensial saya.
Stephen Hawking - Sejarah Singkat Waktu

Jika penerbit Hawking benar, maka menambahkan hanya 33 formula sudah cukup untuk membuat jumlah pembaca potensial mendekati nol. Akankah kita mencoba?

Pertama-tama, perlu untuk mencapai tingkat pemahaman yang memadai tentang notasi. Ingat, matematika adalah bahasa.

Dalam pendekatan pertama, beberapa lapisan pemahaman teks matematika dapat dibedakan. Lapisan pertama adalah pemilihan leksem, yang disebut analisis leksikal. Yang kedua adalah konstruksi ekspresi dan konstruksi semantik lainnya. Pemrogram menyebut ini kata parsing, yaitu parsing, dan matematikawan umum biasanya tidak menyebutnya sama sekali, karena mereka menggunakan mekanisme ini secara tidak sadar. Berikutnya adalah lapisan yang bertanggung jawab untuk memahami area subjek, makna fisik dan semua itu.

Beberapa ahli matematika melihat programmer sebagai non-ahli matematika. Ini tidak adil. Pertama, programmer harus berurusan dengan mesin yang tidak memaafkan kelalaian dalam teks program. Bandingkan dengan artikel ilmiah tipikal, di mana ungkapan "jelas", "mudah ditampilkan", "tidak punya otak", dll. Sering digunakan, tetapi dalam kenyataannya transisinya tidak terlalu jelas. Oleh karena itu, berkat pemrograman, seluruh cabang matematika lahir dikhususkan untuk bahasa formal dan analisis mereka. Kedua, dalam kondisi yang sulit, bahasa pemrograman itu sendiri dan alat terkait telah berkembang. Lihat bagaimana bahasa modern yang elegan menyelesaikan masalah pencocokan variabel dengan objek. Ngomong-ngomong, masalah serius adalah untuk tidak menjadi bingung dalam notasi ketika mereka terlalu banyak, dan mereka datang dari sumber yang berbeda. Dan jika Anda meluangkan sedikit waktu untuk tinjauan singkat tentang bahasa tertentu seperti Coq, Agda, Idris, Anda akan melihat hubungan terdekat antara matematika dan pemrograman itu sendiri.

Analisis leksikal

Saya dulu tahu bagaimana surat ditulis, saya percaya pada kekuatan kata-kata.
Krematorium - Kesempatan Terakhir

Pertama, tanyakan programmer teman apa lexer dan parser itu. Anda tidak perlu masuk terlalu dalam, cukup pahami dengan contoh apa token itu. Jika Anda mendengar kata-kata aneh seperti "el-er-parser" atau "sintaksis pohon", diam-diam tinggalkan ruangan. Kemungkinan besar, Anda sudah memiliki cukup, programmer tidak lagi dibutuhkan. Cerna pengetahuan Anda. Maka Anda perlu belajar bagaimana membedakan token dalam teks matematika nyata. Berlatihlah pada artikel yang diunduh secara acak. Hindari dokumen dalam format selain pdf, dan juga teks yang diletakkan langsung di halaman web. Namun, ada beberapa situs yang diketahui dapat dipercaya bahwa mereka dapat menampilkan teks matematika dengan benar (Wikipedia dan Habr termasuk dalam daftar putih). Buku kertas juga umumnya cocok. Jangan mencoba mengekstrak makna dari teks yang ditemukan, cukup latihlah untuk mem-parsing rumus.

Surat

• Huruf dua huruf biasanya digunakan - Latin dan Yunani, tetapi huruf Sirilik dan Ibrani kadang-kadang ditemukan. Kebetulan huruf-huruf dari huruf yang berbeda bertepatan dalam gaya. Pada surat itu, ini tidak menyebabkan masalah, karena dua huruf berbeda dengan tipe yang sama tidak digunakan dalam teks yang sama. Namun, Anda mungkin menghadapi ejekan matematikawan jika, misalnya, Anda membaca B dengan keras sebagai "menjadi" ketika Anda berarti "beta". Bersiaplah secara psikologis untuk ini, Anda harus bertahan.
• Huruf besar dan kecil mewakili objek yang berbeda. (Bagi sebagian orang, ini kelihatannya terlalu jelas, tetapi saya menganggap perlu untuk mengucapkannya secara eksplisit. Suatu kali saya perlu menyampaikan esensi pekerjaan saya kepada kolega-kolega saya dari departemen paten. Ketika saya hampir mencapai karakter anekdot "ayah, di mana laut?", Saya tiba-tiba menyadari bahwa gadis-gadis menganggap penunjukan saya m dan M untuk merujuk ke objek yang sama. Begitu kesalahpahaman dihapus, seluruh proses, berkat profesionalisme mereka dalam pekerjaan mereka, dengan cepat dan pasti berakhir dengan kesuksesan penuh.)
• Huruf yang sama, ditulis dalam font yang berbeda, berarti objek yang berbeda.

Sebagai aturan (dalam aljabar), satu huruf adalah token independen. Jika beberapa huruf dituliskan berturut-turut, maka multiplikasi tersirat. Sebagai contoh, abc berarti produk a, b, dan c. Namun, ada pengecualian. Pertama-tama, ini adalah nama dari banyak fungsi standar dan notasi lainnya, yang merupakan token multi-huruf: $$$\ sin, \ cos, \ min, \ max, \ sup, \ lim$ dll. Mereka biasanya digambarkan dalam gaya lurus (roman), tidak seperti token huruf lain yang ditulis miring. Selain itu, dalam ilmu komputer dan di beberapa bidang lain, mereka menyimpang dari aturan ini, di mana urutan huruf menunjukkan satu kata token. Jika dalam kasus tertentu bahkan ada keraguan sedikitpun, berkonsultasilah dengan spesialis.

Kurung

Peran paling penting dalam hal parsing dimainkan oleh tanda kurung. Anda mungkin sudah tahu atau menebak bahwa tanda kurung digunakan untuk mengelompokkan token. Namun ada beberapa pengecualian. Jika formula tampak aneh bagi Anda dan mengandung pasangan kurung tambahan, atau bahkan keseimbangan kurung rusak, kemungkinan besar Anda menemukan contoh dengan penggunaan kurung alternatif. Pergi ke spesialis untuk klarifikasi.

Indeks

Perhatikan indeks atas dan bawah. Ini adalah tipografi yang terlihat seperti superskrip dan subskrip. Superskripnya lebih sederhana: sebagai aturan, itu singkatan dari eksponensial. Dengan bagian bawah sedikit lebih keras. Ini dapat dipahami dengan dua cara:

• Seperti operasi pemetaan. Sebagai contoh $$$x_i$ Apakah fungsi seperti itu $$$x$ yang diambil sebagai argumen $$$i$ . Jika sekarang titik ini tidak jelas, tidak apa-apa, tempat ini dapat dilewati untuk saat ini.
• Sebagai cara untuk membentuk token baru ketika surat yang nyaman sudah berakhir. Sering dapat diasumsikan demikian $$$a_1, a_2, a_i$ - ini hanya tiga objek yang berbeda.

Pada titik tertentu, tampaknya bagi Anda bahwa kedua poin ini pada dasarnya adalah hal yang sama. Jangan khawatir, ini normal, Anda telah menjadi sedikit lebih dekat dengan pencerahan. Jadwalkan pertemuan dengan spesialis.

Karakter lainnya

Matematikawan adalah aesthetes. Mereka suka ketika tidak hanya konten tetapi juga bentuk yang indah. Mereka senang ketika formula diketik dalam tipografi yang baik dan cocok. Knut membuat roti jahe lezat yang disebut $$$\ TeX$ . Ikuti tutorial tentang pengetikan dan pengaturan huruf dan temukan tabel simbol di sana. Sekarang penting bagi Anda bagaimana simbol-simbol ini diklasifikasikan: huruf, operator, tanda hubungan, panah ... Tanpa mempelajari makna matematika simbol, cobalah untuk memahami bagaimana simbol dari setiap kelas digunakan secara sintaksis. Sebagai contoh, ada kelas operasi biner yang sama-sama kanan dan kiri dari simbol operasi harus semacam subekspresi.

Tokoh

Non-matematikawan percaya bahwa matematikawan percaya. Bahkan, ahli matematika jarang dipertimbangkan, dan angka digunakan terutama untuk penomoran objek. Tampaknya, oleh karena itu, bagian "Angka" ditambahkan dengan terburu-buru dan secara tidak logis mengikuti bagian "Simbol Lain". Anda sendiri dapat memberi tahu para ahli bagaimana token digital terbentuk dan apa artinya.

Konvensi Notasi

Biarkan a, b, c, d, e, f menjadi bilangan real, di mana e tidak harus sama dengan basis logaritma natural, meskipun mungkin bertepatan dengan itu.

Dalam matematika, ada konvensi tentang karakter mana yang akan digunakan dalam kasus apa. Namun, di berbagai bagian perjanjian ini dapat bervariasi. Itu seperti dialek bahasa. Ada notasi standar di semua matematika. Lihatlah konvensi yang diterima di area subjek Anda. Selain itu, beberapa sarjana lalai dan terkadang melanggar perjanjian yang berlaku umum. Sayangnya, dalam kebanyakan kasus tidak ada set aturan tentang hal ini, Anda dapat mendiskusikan hal ini dengan dokter spesialis Anda sesekali.

Meskipun matematika umumnya supranasional, ada perbedaan budaya. Anda mungkin menemukan mereka jika Anda menyimpang terlalu jauh dari rute yang disarankan oleh Panduan. Misalnya, penunjukan fungsi tangen, cotangent, hiperbolik dalam bahasa Inggris dan Rusia dibedakan. Juga, huruf yang sama dapat diucapkan secara berbeda tergantung pada tradisi budaya. Untuk menghemat upaya, pelajari nama-nama bahasa Inggris dari semua huruf, termasuk Yunani. Jika Anda belum bolos sekolah, maka setidaknya tidak akan ada masalah dengan alfabet Latin. Jika Anda menggunakannya dalam bahasa Rusia, lawan bicara Anda mungkin mengerutkan kening, tetapi kali ini mereka harus bertahan. Jika Anda ingin membuat mereka bahagia, pelajari nama-nama huruf Latin dan Yunani yang diterima dalam budaya matematika berbahasa Rusia.

Parsing

Ekspresi

Anda kemungkinan besar pernah mendengar istilah "pohon" tidak dalam bahasa botani, tetapi dalam pengertian matematika. Ini adalah hal yang cukup sederhana, jika perlu, menyegarkan pengetahuan Anda. Jadi, ekspresi matematis memiliki struktur pohon. Ini berarti bahwa ekspresi terdiri dari subekspresi yang terdiri dari subekspresi ... Tetapi proses ini bukan tanpa akhir, tetapi berakhir dengan beberapa subekspresi yang terdiri dari token.

Beberapa token sendiri adalah ekspresi dasar. Misalnya, angka (lebih tepatnya, literal angka) dan variabel. Dan beberapa mengharuskan argumen ditambahkan ke mereka di posisi tertentu, yaitu, semacam subekspresi. Kemudian mereka membentuk ekspresi yang lebih besar. Misalnya, simbol operasi penjumlahan memerlukan ekspresi di sebelah kanan dan kiri. Kita dapat mengatakan bahwa leksem memiliki arity atau, jika Anda lebih suka chemistry, valency, adalah berapa banyak dan di tempat apa Anda perlu menambahkan leksem dari subekspresi untuk membentuk sebuah ekspresi. Untuk operasi + arity dapat dijelaskan sebagai berikut: $$$\ cdot + \ cdot$

Entri ini persis berarti bahwa + token memerlukan argumen di sebelah kiri dan kanannya. Token yang berbeda memerlukan jumlah argumen yang berbeda, di samping itu, lokasi argumen tidak terbatas pada "kanan" dan "kiri", tetapi dapat, misalnya, "atas", "bawah", "kanan-bawah". Ada juga token majemuk yang sudah ada sejak zaman kuno , tetapi mixfix mendapat nama khusus sebagai bahasa pemrograman yang dikembangkan. Misalnya, produk skalar vektor dinotasikan sebagai berikut: $$$\ langle \ cdot, \ cdot \ rangle$ .

Terkadang token konflik karena mereka tidak dapat memutuskan untuk siapa argumen yang ditulis di antara mereka. Maka Anda harus menambahkan tanda kurung.

Variabel

Beberapa token memiliki makna yang dikaitkan dengan mereka dari atas - baik di suatu tempat yang lebih tinggi dalam teks, atau oleh tautan di teks lain. Atau maknanya tersirat sebagaimana diterima secara umum dalam disiplin ilmu tertentu atau dalam semua matematika. Misalnya, simbol plus menunjukkan operasi penambahan. Plus - dia di Afrika plus. Namun, mungkin di suatu tempat yang lebih dekat ke ujung rute Anda, Anda akan menemukan simbol plus dengan beberapa makna yang tidak biasa. Masih ada token (biasanya alfabet) yang tidak ditunjukkan secara eksplisit oleh apa pun, mereka disebut variabel, yang ada beberapa jenis.

• Parameter Ini adalah variabel yang dikatakan ditandai oleh sesuatu, tetapi tidak dikatakan apa sebenarnya. Jika itu terasa aneh bagi Anda, Anda dapat melewatkannya untuk saat ini, dan ketika Anda memenuhi parameter, Anda akan segera memahami semuanya dengan contoh.
• Variabel gratis. Jika variabel ditemukan dalam ekspresi tentang yang tidak ada yang dikatakan, maka variabel seperti itu disebut gratis. Sebenarnya, sama sekali tidak ada yang bisa dikatakan. Anda memiliki hak untuk bertanya kepada pembuat rumus yang darinya variabel bebas diambil. Jangan ragu untuk bertanya, ini berguna: bahkan jika penjelasannya ternyata tidak bisa dimengerti, mereka akan menganggap Anda sedikit lebih serius.
• Variabel terikat. Jika Anda tidak menyukai libertine variabel bebas, ada beberapa cara untuk membatasi kebebasannya. Anda bisa menambahkan sesuatu ke ekspresi, sehingga Anda mendapatkan ekspresi baru di mana variabel yang sebelumnya bebas dikunci. Dan ekspresi baru, tidak seperti yang lama, tidak lagi bergantung pada variabel ini. Jika Anda ingin tahu apa "sesuatu" ini, lihatlah bilangannya atau pada integral tertentu. Cobalah untuk melihat hanya pada sintaks, tidak menggali maknanya, tetapi, Anda tahu, membuat ketagihan.

Konteks

Kebetulan, melihat formula, tidak mungkin membedakan variabel bebas dari parameter. Ini berarti bahwa informasi tambahan perlu diambil dari konteks, yang biasanya diungkapkan oleh formula atau teks lain dalam bahasa manusia. Tergantung pada konteksnya, rumus tersebut mungkin memiliki arti yang berbeda. Jika Anda perlu memahami rumusnya, selalu pelajari konteksnya dan cari pengertian.

Namun, rumus dapat ada tanpa konteks, hanya sebagai objek sintaksis di mana transformasi dapat dibuat. Matematikawan sering kali dapat menggeneralisasi - “melupakan” konteksnya, kemudian membuat perhitungan, kemudian “mengingat” konteksnya dan memahami kembali makna formula yang diperoleh.

Simbol sama dengan

Tanda sama sangat penting. Ini digunakan dengan cara yang berbeda, dan Anda harus dapat membedakannya.

• Penilaian suatu variabel berdasarkan nilai. Ini adalah ketika variabel di sebelah kiri dan ekspresi di sebelah kanan. Dalam beberapa disiplin ilmu, dalam kasus seperti itu, alih-alih = mereka menulis: = atau bahkan :: =.
• Identitas. Di sebelah kiri dan di sebelah kanan ada beberapa ekspresi, dan orang yang menulis ini mengklaim bahwa kedua ekspresi itu sama. Simbol juga digunakan di sini. $$$\ equiv$ . Sudahkah Anda memikirkan apa artinya "sederajat"? Layak untuk didiskusikan, tetapi mungkin membawa Anda jauh dari rute.
• Persamaan. Ini adalah cara untuk menggambarkan entitas baru yang fundamental. Matematikawan melakukannya dengan cara ini: mereka mengambil beberapa variabel bebas, membangun ekspresi di atasnya dan mengarahkan mereka ke dalam persamaan atau bahkan ke dalam sistem beberapa persamaan, sehingga mereka bahkan lebih dekat. Dan kemudian mereka menyaksikan bagaimana variabel-variabel malang ini bergegas dalam kendala, membentuk set yang aneh. Dan kemudian mereka mempelajari perangkat ini dengan penuh minat. (Omong-omong, rute Anda melewati wilayah teori himpunan, Anda harus mengenal mereka lebih baik.) Untuk menggambarkan himpunan yang diperoleh adalah menyelesaikan persamaan. Anak-anak di sekolah biasanya diberi persamaan yang memunculkan set elemen yang sangat sederhana, kadang-kadang dua atau tidak sama sekali. Tetapi ilmuwan dewasa dalam hal ini adalah penghibur besar. Dan beberapa fisikawan mampu menghasilkan seluruh alam semesta dengan satu persamaan.

Mengekstrak makna dari formula

Ada yang ditulis, tetapi dalam kurung OH. Mereka mencoba - dan sungguh, OH.

. . ?

, . , . , , ́, ́, ́ ́. : , . , , . , - , , , — , , , .

, , . .

- , - , . . , «- », : « », «», « », « » ..

, , , …
—

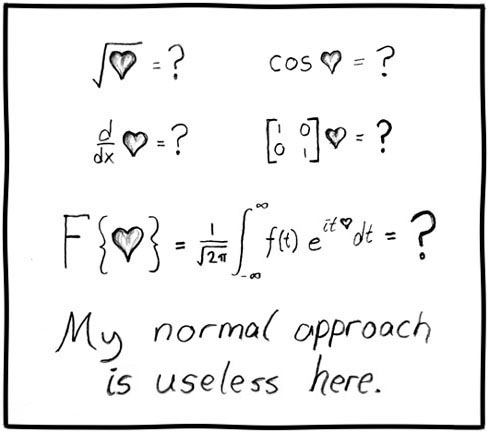
XOR , ?

, . .

, , , . , . , , , , , , .

- , from. , , , , , . , .

, . — ( ), , . , , , . , .

, . , , . , , , .

, , - - . - (, computer science) . , .

— . — .
, -

, . , , . . .

, . . , . , . , , - , . « ». , . , . « ?».

, . $$$a^b$ . : a — , b — , , , . : , .

, .

. «», « » « », . , , . , . , , . , , . , . . : $$$\infty$ . , — . . : ! ! - , , . — , .

• . . .
• . . , ? -.
• . , . -, , , .
• . . , - - .
• , « ». , . , . , .
• , . , . , , .

Kembali ke kotak pasir set terbatas, periksa sekali lagi seberapa baik Anda mengingat notasi. Bermain dengan set terbatas ukuran kecil. Cobalah untuk menerapkan operasi dasar pada mereka. Bangun banyak himpunan bagian. Jika Anda lupa apa itu bijih , segarkan pengetahuan Anda dalam buku pelajaran untuk anak-anak prasekolah. Lagi pula, Anda tahu konsep ini dari periode pra-pidato, saat itu tidak dipanggil dengan cara apa pun, bukan? Pastikan intuisi Anda selaras dengan definisi dan pernyataan dasar. Jika ini bukan masalahnya, hubungi spesialis.

Sebelum pergi, lihat sekeliling lagi. Di tepi kotak pasir Anda dapat melihat sudut ultrafinitif. Semuanya sederhana dengan mereka. Katakan halo kepada mereka, jangan katakan bahwa Anda pergi ke luar kotak pasir.

Sekali lagi tentang notasi

betapa sulitnya hidup di antara orang-orang yang membosankan
kata Michael yang berusia tiga tahun
di antara membosankan
dikoreksi Igor, tiga puluh dan memakai kacamata

Grup Abelian -> ruang linear -> operator -> fungsional dalam ruang linear. Tetapi setelah mengunduh cabang ini, Anda dapat memicu kata "fungsional" dalam deskripsi fungsi perangkat lunak.

Anda sudah tahu beberapa istilah matematika dan akan terus belajar lebih banyak. Cobalah untuk tidak menggunakannya dengan sia-sia ketika berkomunikasi dengan spesialis tentang topik yang relevan. Misalnya, alih-alih ungkapan "grup metode", untuk berjaga-jaga, lebih baik untuk mengatakan "set metode" atau "set metode" sehingga tidak ada yang akan berpikir bahwa Anda telah membangun operasi pada serangkaian metode yang memenuhi aksioma grup. Jika selama komunikasi informal pada topik matematika Anda kehilangan kata-kata umum karena fakta bahwa mereka sibuk dengan istilah, lebih baik menggunakan variabel metasyntactic yang disebut: "sampah", "omong kosong", "shnyaga", dll., Mereka juga dapat secara emosional cat dengan kata sifat: "canggung", "halus", "sakit-sakitan." Kedengarannya tidak terlalu cerdas, tetapi Anda lebih cenderung mengerti. Setelah beberapa waktu, Anda akan menyingkirkan kata-kata pengganti yang jelek, dan ucapan Anda tidak akan menyusahkan para ahli filologi atau ahli matematika.

Jangan gunakan quantifier universal dengan sia-sia. Kuantitas universalitas yang diekspresikan dalam bahasa biasa diwakili oleh kata-kata "selalu," "semua," "semua," "semua orang," "apa saja," dll. Kata-kata "tidak pernah", "tidak ada tempat", dll. mereka juga mewakili pengukur ini, tetapi dengan negasi, yaitu, "tidak pernah" berarti "selalu tidak." Matematikawan sering menafsirkan pernyataan dengan kuantifikasi universalitas secara harfiah, setelah itu, setelah menyajikan contoh tandingan, mereka membuktikan kesalahan formal Anda. Anda tidak perlu stres ekstra? Tentu saja, ada kasus-kasus ketika quantifier universal dapat dan harus digunakan.

Dalam matematika, sering ada homonim. Ini adalah ketika satu kata atau simbol menunjuk beberapa konsep yang sama sekali berbeda. Pertama, ini karena kurangnya kata-kata dan karakter yang baik. Kedua, tidak seperti bahasa alami, konsep yang sangat sering berbeda setelah beberapa generalisasi ternyata praktis sama. Matematikawan yang memperhatikan bahwa ini sama dengan ini sering dapat mengalami orgasme otak dari kesadaran ini. Terutama sensasi kuat muncul jika peneliti telah melakukan bagian penting dari jalan menuju kesadaran sendiri. Mungkin saja Anda juga akan mengalami sensasi kuat yang sama. Tetapi jika tidak, tidak apa-apa, itu juga baik-baik saja. Silakan berbagi perasaan Anda dengan para ahli.

Biasanya homonimi tidak membuatnya sulit untuk dipahami, karena ahli matematika dengan hati-hati memastikan bahwa semua definisi adalah ketat dan benar.

Logika

Anda harus bekerja hampir secara eksklusif dengan objek akhir. Ini berarti bahwa ide-ide intuitif Anda tentang logika kemungkinan besar sudah cukup dan, yang paling penting, tidak akan mengarah pada kontradiksi. Untuk jaga-jaga, baca tentang mode ponens, bahkan jika namanya tidak Anda kenal, Anda pasti tahu intinya.

Secara umum, logika adalah tentang bagaimana membuat pernyataan baru berdasarkan yang sudah ada. Lihatlah sekeliling. Di mana-mana di sekitar Anda ucapan: besar, kecil, jelas, tidak bisa dipahami. Anda dapat mengasumsikan bahwa pernyataan dibagi menjadi dua jenis: benar dan salah. Dan inilah patung-patungnya! Bagaimana kamu suka itu?

$$

$$\ int e ^ x = f (u_n)$$

Pernyataan ini tidak benar atau salah, tidak ada artinya (setidaknya dari sudut pandang matematika), karena apa yang ditulis di sebelah kiri tanda sama dengan itu bukanlah ekspresi. Anda dapat menambahkan dx ke integral, tetapi kemudian beberapa variabel bebas tetap, karena itu ekspresi bukan pernyataan. Mereka harus berarti sesuatu atau membuat mereka terhubung, sehingga kita dapat berbicara tentang kebenaran.

Yah, mari kita pertimbangkan hanya pernyataan yang bermakna. Haruskah mereka benar atau salah? Ternyata tidak. Beberapa pernyataan tidak dapat dibuktikan atau disangkal, mereka disebut tidak dapat diselesaikan. Komentar yang tidak dapat dipecahkan tidak mungkin ditemui di jalan Anda. Namun, mereka pasti akan menemukan kebenaran yang sejauh ini tidak ada yang tahu.

Jika Anda tidak mematuhi yang terakhir kali dan melihat ke jurang dasar-dasar matematika, Anda mungkin dapat memperhatikan bahwa ada lebih dari satu logika, dan ada banyak yang berbeda. Untungnya, dalam perjalanan pengetahuan Anda, menghasilkan banyak kesedihan, tidak akan dibutuhkan. Jika Anda merasa nyaman meyakini bahwa kebenaran selalu sama, teruslah berpikir demikian.

Teori kategori

"Deoksiribonukleat," kataku. - Ini asam. Deoksiribonukleat.
Dia tersenyum sedih, menyesuaikan pince-nez-nya.
"Asam," dia mengulangi dengan suara yang dicegat. "Kenapa dia seperti itu?"
"Anda tidak bisa memanggilnya sebaliknya," kataku dengan simpatik. "Kecuali disingkat DNA." Ya, Anda melewatkannya, Fedya, baca terus.
"Ya, ya," katanya. "Aku lebih baik melewatkannya."
Arkady dan Boris Strugatsky - The Tale of the Three

Meskipun teori kategori itu sendiri hampir sama berbahayanya dengan teori himpunan, kita perlu mengekstraksi beberapa konsep yang secara resmi berhubungan dengan bagian ini.

• Kelas adjuster. Ini adalah salah satu cara untuk membangun struktur baru dari yang sudah ada. Baca definisi, lihat beberapa contoh. Jika tidak jelas, Anda bisa melewati. Tetapi jika Anda masih melakukan penetrasi, Anda akan mendapatkan bonus untuk memahami hal-hal lain. Misalnya tentang cincin $$$\ mathbb {Z} _n$ (hal ini akan dibutuhkan sedikit kemudian) lebih mudah untuk berpikir sebagai kelas deduksi, dan bukan sebagai hasil dari operasi mengambil sisa divisi. Juga, definisi sekolah tentang vektor sebagai segmen dengan panah akan tampak konyol dan bahkan salah bagi Anda. Anda dapat mengajari teman-teman Anda bahwa vektor bukan segmen, tetapi kelas segmen.
• Morfisme. Morfisme adalah beberapa hubungan antara sepasang benda. Anda tahu satu jenis morfisme semacam itu dari sekitar usia tiga - ini adalah penipisan antara set terbatas. Baca definisi isomorfisme dan sadari bahwa ini adalah kasus penistaan ​​yang lebih umum. Dapatkan pemahaman yang baik, ini penting. Jika perlu, konsultasikan dengan spesialis. Lebih jauh Anda dapat membaca tentang homomorfisme (jangan dikacaukan dengan homeomorfisme!). Jika ada homomorfismofobia atau kesulitan lain, Anda dapat melewati.

Secara umum, seluruh teori kategori adalah bagian matematika yang paling abstrak, tidak ada apa pun di sana kecuali hal-hal kecil dan panah. Meskipun ada beberapa bahaya pada jiwa, teori kategori dapat direkomendasikan untuk terapi substitusi jenis kecanduan lainnya. Namun, jangan mengobati sendiri, di kota Anda, kemungkinan besar, ada spesialis yang tersedia.

Aljabar

Jujur, saya tidak curiga bahwa selama lebih dari empat puluh tahun saya telah berbicara dalam prosa.
Jean-Baptiste Moliere - Pedagang di kaum bangsawan

Nama disiplin harus akrab dengan Anda dari sekolah. Bahkan, aljabar bekerja dengan struktur aljabar, dan di sekolah hanya bilangan bulat dan bilangan rasional yang lulus dari struktur, serta (dalam bentuk yang sangat terpotong) yang nyata. Berita baiknya adalah sekarang Anda tidak perlu menyelesaikan persamaan aljabar yang menyiksa Anda di sekolah. Jika ada yang muncul di jalan Anda, maka itu sudah diputuskan. Jika ada, komputer akan menghitung untuk Anda, itu besi. Anda harus berkenalan hanya dengan beberapa struktur aljabar tertentu.

Pertama-tama, penting untuk memahami dengan jelas konsep struktur aljabar . Baca definisi, dapatkan pemahaman yang baik. Tinjau definisi grup . Dalam memuatnya adalah definisi dari semua subkelompok, seperti monoids, semigroups, groupoids. Baca juga, tapi jangan repot-repot mengingat. Anda hanya perlu grup. Selanjutnya, pelajari definisi cincin dan bidang .

Perhatian! Hindari tempat-tempat di mana struktur dengan pembawa yang tak terbatas dinyatakan secara eksplisit. Kami masih membutuhkan beberapa objek tak berujung seperti itu, tetapi Anda akrab dengannya. Yaitu: cincin bilangan bulat $$$\ mathbb {Z}$ , bidang bilangan rasional $$$\ mathbb {Q}$ dan bidang bilangan real $$$\ mathbb {R}$ . Bermainlah dengan mereka, ingat peraturan sekolah seperti “jumlahnya tidak berubah dari mengubah ketentuan persyaratan” dan membenarkan fakta bahwa struktur ini benar-benar cincin / bidang. Jelaskan mengapa bilangan bulat tidak membentuk bidang.

Karena tujuan akhir panduan ini adalah kriptografi elips, Anda harus membiasakan diri dengan konsep polinomial di atas bidang . Agar tidak mempelajari definisi umum, hubungi spesialis sehingga ia hanya memberi tahu apa yang relevan dengan tujuan perjalanan Anda.

Jika Anda lebih suka geometri daripada aljabar, Anda bisa melihat kurva eliptik di atas bidang $$$\ mathbb {R}$ . Namun perlu diingat bahwa, terlepas dari namanya, objek-objek visual ini sepenuhnya jauh dari jalan Anda.

Untuk kepentingan, Anda juga dapat merenungkan definisi struktur aljabar lainnya: aljabar (ya, aljabar adalah struktur aljabar seperti itu; jangan khawatir, ini bukan rekursi, tetapi hanya homonim), ruang vektor (linier) ...

Kembali ke rute. Anda sedang menunggu kolom terakhir . Baca artikel tentang mereka. Sebenarnya tidak semua yang dibutuhkan. Ini adalah kasus lain ketika, untuk menghemat usaha, lebih baik segera mencari saran dari spesialis. Menyadari klasifikasi bidang terbatas, ini sederhana. Ngomong-ngomong, akan menarik untuk mengetahui mengapa ladang yang terbatas juga disebut ladang Galois. Ingat apa yang Anda lakukan dalam 20 tahun, dan malu.

Jika Anda suka trolling, dan Anda menghargai kemampuan Anda, cobalah mengenali bourbacists dan anti-bourbacists di forum tematik dan kumpulkan bersama.

Teori informasi

Jika Anda dilahirkan setelah tahun 1970, kemungkinan besar Anda diberi tahu di sekolah menengah tentang bit dan byte. Bytes dalam ilmu dasar tidak terlalu dibutuhkan, tetapi konsep sedikit perlu diketahui dengan jelas. Lihatlah buku teks jika perlu.

Hitung atau cari tahu di buku teks berapa banyak urutan bit total dari panjang yang diberikan. Bermain dengan alfabet dengan menyandikan huruf dalam urutan bit. Pikirkan atau baca di buku teks cara membuat kode bilangan bulat. Pertimbangkan apa yang berguna dalam teori informasi adalah logaritma basis dua.

Teori probabilitas

Siapa pun yang memiliki kelemahan dalam metode aritmatika untuk mendapatkan angka acak adalah berdosa tanpa keraguan.
John von Neumann

Kesalahpahaman teori probabilitas dan penerapannya pada isu-isu praktis adalah sumber kesalahan manusia yang paling penting. Ini adalah topik yang sangat penting, coba curahkan waktu untuk membiasakan diri dengan dasar-dasarnya. Belum tentu saat ini, karena untuk tujuan akhir rute kami, hanya satu dari sub-bagian yang diterapkan yang cukup - pembuatan angka acak.

Sekarang cukup bagi Anda untuk menyadari bahwa masalah menghasilkan bilangan acak sangat rumit, seluruh lembaga telah menanganinya selama beberapa dekade. Bahkan menentukan peluang itu sangat rumit. Anda tidak bisa hanya mengambil dan mengambil nomor acak. Sayangnya, ada jebakan bahasa yang membuatnya sulit untuk memahami topik. Kata acak, serta yang setara dengan Rusia, "acak", meskipun pada tingkat lebih rendah, pada dasarnya berarti "mengerikan", sedangkan untuk banyak aplikasi, terutama untuk kriptografi, Anda harus memilih jauh dari acak.

Jika Anda memahami teori probabilitas dengan baik, temui spesialis. Jika waktu mengizinkan, pergilah untuk melihat interpretasi multi-dunia (Everett) dari mekanika kuantum. Jangan terbawa suasana, Anda sedang menunggu di rumah.

Teori komputabilitas

Apakah mungkin membuat kompiler ini selalu memperingatkan bahwa program dapat berjalan dalam siklus?

Anda tidak akan memerlukan bagian ini sekarang. Sangat berguna untuk menyadari bahwa tidak untuk fungsi yang didefinisikan secara matematis, ada algoritma yang menghitungnya. Jika Anda merasakan kekuatan dalam diri Anda, bertamasya melalui sejarah masalah, cobalah untuk memahami definisi dan hasil dasar. Jangan terlalu banyak bekerja, topik ini opsional.

Hanya untuk mengurangi stres Anda dari realisasi ketidaktahuan Anda sendiri, saya akan memberi tahu Anda bahwa pertanyaan yang diajukan dalam epigraf itu diajukan kepada saya oleh seorang profesor fisika dan matematika yang disegani, yang bidang minatnya agak jauh dari ilmu komputer. Jika Anda memahami situasi anekdotal, perjalanan Anda bermanfaat. Dorong diri Anda.

Teori kompleksitas

Sayangnya, sains klasik telah berevolusi sehingga teori kompleksitas, secara tegas, didasarkan pada teori batas dari analisis matematika. Ini semua karena matematikawan yang egois belum merawatmu. Mereka mendekati kompleksitas, sudah berdiri di atas bahu para raksasa, dan menggunakan alat yang mereka sendiri miliki dengan sempurna. Untuk tujuan-tujuan sederhana kita, adalah mungkin untuk membangun teori kompleksitas kecil kita sendiri yang terpisah, yang bahkan diinginkan oleh para ultrafinitif. Tapi, misalnya, saya tidak memiliki kekuatan maupun motivasi untuk menyelesaikan membangun sepotong lanskap yang adil. Karena itu, Anda masih harus beralih ke apa yang disebut kata matan.

Analisis matematis

Saya bukan botan, saya hanya suka matan.

Baca definisi batas urutan (Anda tidak perlu batas fungsi). Ganti semua ekspresi seperti "ruang ini-dan-itu" dengan "seperangkat bilangan real", matematikawan suka menggeneralisasi, tetapi Anda tidak membutuhkannya. Pastikan Anda dapat menguraikan ekspresi yang memiliki kata $$$\ lim$ . Kemungkinan besar, Anda akan mengalami kesulitan, ini normal. Percayalah, konsep batas sangat intuitif, Anda hanya perlu merangsang bagian yang sesuai dari intuisi Anda. Mintalah spesialis untuk mengomentari teks definisi. Gambarlah, mainkan dengan urutan sederhana. Jika waktu mengizinkan, pergi bertamasya untuk melihat batas luar biasa kedua.

Bahkan jika Anda tidak memiliki pemahaman penuh tentang batas, Anda dapat segera melanjutkan ke notasi-O. Anda hanya perlu "O" besar , tetapi bebannya "O" kecil dan segala macam theta dan omega. Jangan terlalu banyak bekerja, untuk permulaan Anda hanya perlu secara kasar memahami apa itu $$$O (1), O (N), O (\ log N)$ . Cari tahu, tapi coba tebak sendiri mengapa $$$O (\ log N)$ hanya logaritma, bukan logaritma karena alasan tertentu. Kemudian istirahat sedikit dan pegang di tangan Anda $$$O (N ^ 2)$ dan $$$O (2 ^ N)$ . Lihatlah $$$O (N ^ k)$ (ingat konteksnya: di sini N adalah variabel, k adalah parameter). Pikirkan mengapa mereka berbicara tentang pertumbuhan polinomial ketika $$$N ^ k$ - hanya monomial, yaitu, kasus polinomial khusus, tetapi mereka tidak menempatkan banyak polinomial penuh di bawah "O". (Bahkan jika Anda tidak berbicara bahasa Latin, Anda mungkin sudah menebak bahwa polinomial sama dengan polinomial, dan monomial adalah monomial.) Petunjuk: alasannya sangat mirip dengan yang “hanya logaritma” dan bukan “logaritma yang mana ke tanah. " Hubungi spesialis untuk mengklarifikasi masalah ini. Belajarlah untuk membandingkan "O" ini satu sama lain.

Catatan: o-notasi adalah contoh langka ketika notasi matematika tidak konsisten. Dalam catatan $$$f (N) = O (N)$ tanda sama digunakan, sementara itu menyiratkan sesuatu yang lain, yaitu: "fungsi $$$f (N)$ milik kelas $$$O (N)$ ". Artinya, tanda asimetris harus digunakan $$$\ dalam$ tapi itu tradisi. Nah, sekarang Anda melihat bahwa matematikawan tidak berdosa. Mungkin akan menjadi sedikit lebih mudah bagi Anda untuk menyadari fakta ini.

Teori kompleksitas komputasi - lanjutan

Logaritma - fungsi, pada prinsipnya, terbatas.

Setelah sedikit memasukkan matan, Anda dapat dengan mudah menguasai skala untuk mengukur kompleksitas asimptotik. Kompleksitas algoritma biasanya diukur dalam hal waktu pelaksanaannya: kadang-kadang mereka berbicara tentang waktu yang biasa diukur menggunakan jam (well, kapan tab browser ini memuat?), Kadang-kadang tentang jumlah siklus prosesor atau langkah-langkah komputer abstrak. Mereka yang lebih condong ke fisika lebih suka mengukur kompleksitas dalam satuan energi, misalnya, dalam jumlah bahan bakar diesel yang dikonsumsi untuk mesin Turing. Semua metode pengukuran ini kira-kira setara. Penting untuk mengetahui bagaimana waktu yang dihabiskan (atau energi) tergantung pada ukuran data input dari algoritma. Ini adalah N di bawah "O" besar dalam perkiraan asimptotik dan merupakan ukuran dari data input, dinyatakan dalam bit. Spesialis sepakat untuk mempertimbangkan bahwa jika kompleksitas algoritma tumbuh tidak lebih cepat daripada polinomial, maka itu "mudah", atau "sulit". Sangat tepat di sini untuk kembali sedikit dan ingat bagaimana membandingkan fungsi satu sama lain dalam hal kesejukan, yaitu, dalam hal kecepatan pertumbuhan asimptotik.

Jika Anda memperhatikan bahwa pernyataan yang dibuat dalam prasasti itu salah, dorong diri Anda. Dia dikirim oleh seorang guru universitas dalam metode komputasi. Mengetahui konteks ini, pikirkan secara spesifik apa yang ada dalam pikirannya.

Fungsi satu arah. Baca definisi. . , , , .

, , . , . , . ?

«». « », — « ». <…> . <...> . , , .
—

, . ! , , (, , ). , . - . , . ? . , ?

Ucapan Terima Kasih

, . Shapelez .