Pembenaran matematis dari ketidakcocokan menjalankan eskalator di kereta bawah tanah

Bertentangan dengan aturan penggunaan kereta bawah tanah, untuk menghemat waktu, kita masing-masing berlari setidaknya sekali dalam hidup kita di eskalator. Sekilas, sepertinya ini benar-benar logis dan benar: jika Anda ingin pergi lebih cepat - cobalah untuk berada di platform sedini mungkin. Namun, segera skenario berikut muncul dalam pikiran: Anda menaiki eskalator, turun ke peron, dan pintu mobil menutup tepat di depan hidung Anda. Saat Anda sedang menunggu kereta berikutnya - orang-orang yang naik eskalator pada saat yang sama dengan waktu Anda berdiri diam-diam turun dan naik kereta berikutnya. Dalam hal ini, tidak ada keuntungan. Jadi seberapa rasionalkah menjalankan eskalator dan layakkah melakukannya? Saya cepat-cepat menyenangkan Anda - jawabannya ditemukan! Di bawah ini adalah pembenaran matematis untuk inexpediency (ya, itu TIDAK) untuk menjalankan eskalator di kereta bawah tanah.

Pernyataan tugas

Sebelum beralih ke penalaran matematis, perlu disebutkan bahwa, tentu saja, saya bukan yang pertama berpikir tentang masalah ini sama sekali. Di Internet, Anda dapat menemukan cukup banyak artikel dan bahkan berita tentang saluran federal tentang topik ini. Namun, setiap kali esensi dari eksperimen semacam itu terletak pada lari eskalator yang biasa dengan perbandingan waktu yang diperoleh dengan waktu orang yang berdiri di eskalator. Sedikit lebih baik jika penulis mencoba menilai efektivitas lereng. Lebih baik lagi jika mereka masih menyediakan statistik. Untuk statistik, omong-omong, saya akan mengucapkan terima kasih khusus sedikit lebih rendah. Sehubungan dengan kurangnya kejelasan eksperimen ini dan kurangnya kesimpulan praktis, saya dikandung, dan kemudian dilakukan, analisis proses yang sedang berlangsung.

Maka, kami merumuskan kondisi masalah dan menunjukkan batasan:

1. Eksperimen (mental) melibatkan dua orang yang mendekati eskalator pada saat yang bersamaan pada waktu yang acak dan tidak tahu di mana kereta itu berada.
2. Salah satu dari orang-orang ini berdiri di eskalator dan menghabiskan waktu dengan turun. $$ sama dengan waktu pergerakan eskalator.
3. Yang kedua mempercepat eskalator, meningkatkan kecepatannya masuk $$ kali, dengan demikian mengurangi waktu keturunan dengan jumlah kali yang sama: $$ .
4. Efektif dianggap sebagai penurunan yang dipercepat, yang menyebabkan fakta bahwa orang yang berdiri di eskalator tidak punya waktu untuk naik kereta, di mana orang yang berlari di eskalator memiliki waktu untuk naik.
5. Ditunjukkan oleh $$ - probabilitas keturunan yang efektif. Kemudian, menurut kesetimbangan Nash, seseorang siap untuk mengambil kesempatan dan berlari menuruni eskalator hanya jika probabilitas keturunan efektif lebih besar atau sama dengan probabilitas keturunan yang tidak efektif atau berhenti di tempat, yaitu 0,5. Jika probabilitas keturunan efektif lebih besar dari atau sama dengan 0,5, keputusan untuk menjalankan eskalator akan disebut tepat . Jika kurang dari 0,5 - tidak praktis .
6. Kami mengabaikan fakta bahwa dalam kehidupan nyata, sebagai suatu keharusan, perlu untuk pergi lebih jauh ke mobil setelah meninggalkan eskalator atau menunggu orang untuk meninggalkan mobil, kereta pergi pada interval yang bervariasi dan berdiri tanpa bergerak sebelum membuka dan setelah menutup pintu, yaitu, kita akan berasumsi bahwa jika kereta berdiri di stasiun pada saat meninggalkan eskalator, maka pintunya terbuka dan peserta dalam eksperimen langsung berakhir di mobil, kereta itu sendiri membuka (menutup) pintu dan tiba (pergi) ke stasiun (dari stasiun) secara instan dan dnomomentno.

Kemajuan keputusan

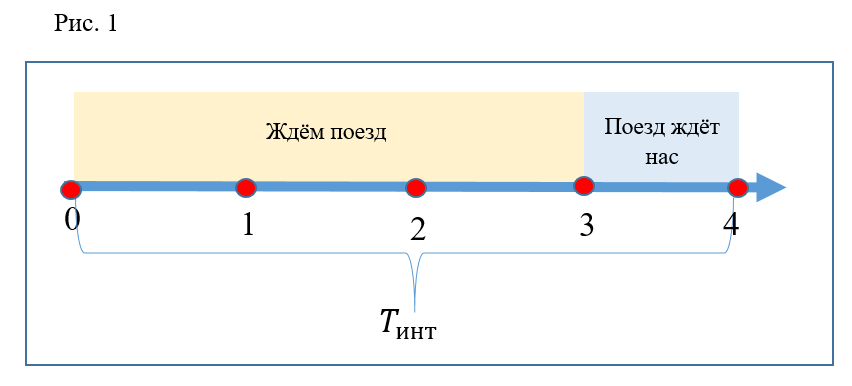
Mari kita menggambar sumbu waktu (Gbr. 1). Seluruh sumbu akan menjadi interval berurutan antara kereta. Selanjutnya, hanya satu interval yang akan dipertimbangkan. Bagilah interval yang ditampilkan menjadi 4 segmen yang sama. Titik 0 pada sumbu ini sesuai dengan saat kereta meninggalkan stasiun. Poin 3 sesuai dengan kedatangan kereta dan pembukaan pintu. Poin 4 - menutup pintu dan keberangkatan kereta. Dengan demikian, untuk kenyamanan representasi grafis dan perhitungan, interval antara kereta dihitung antara saat-saat keberangkatan kereta dari stasiun. 3 segmen pertama adalah waktu penumpang dipaksa untuk menunggu kereta yang tiba. Segmen keempat adalah waktu pemberhentian kereta, ketika penumpang bisa menaikinya. Masukkan juga waktu itu $$ (waktu turun pada eskalator) sama dengan dua segmen. Koefisien $$ sama dengan 2, yaitu, waktu keturunan berjalan 2 kali lebih sedikit dan sama dengan satu segmen.



Sekarang, untuk menentukan probabilitas $$ , cari tahu dalam jangka waktu berapa keputusan untuk pergi jogging akan mengarah pada kenyataan bahwa keturunan akan efektif. Misalnya, jika peserta kami mendekati eskalator pada waktu 0, maka yang pertama akan berada di platform pada waktu itu $$ (Gbr. 2), dan yang kedua sebelumnya, saat ini $$ . Tetapi, seperti yang dapat dilihat dari gambar, pada saat-saat seperti ini tidak ada kereta di stasiun, yang berarti berlari tidak efisien.



Pertimbangkan kasus lain (Gbr. 3): peserta dalam eksperimen mendekati eskalator pada waktu 2. Seperti pada kasus sebelumnya, yang pertama akan berada di platform pada waktu $$ , dan yang kedua sebelumnya, saat ini $$ . Tetapi jelas bahwa di kedua waktu kereta ada di stasiun. Jadi, keduanya akan memiliki waktu untuk naik kereta yang sama, oleh karena itu, berlari sama tidak efisiennya.



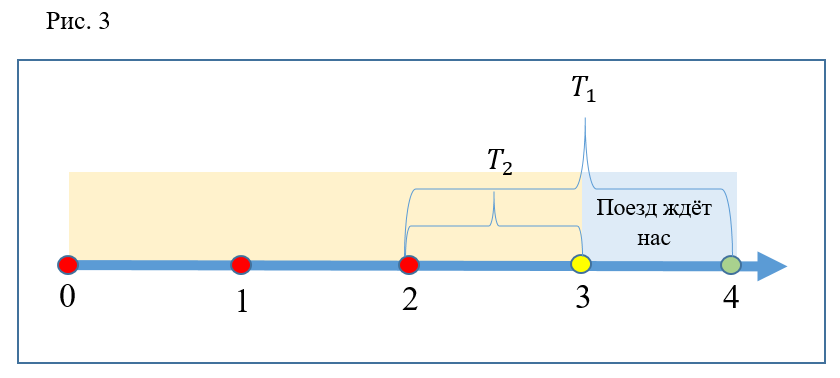
Lebih lanjut, mudah dipahami bahwa setiap saat dalam interval dari 2 hingga 3, efektif untuk berlari turun, karena orang yang melarikan diri selalu berhasil naik kereta, dan bukan yang melarikan diri. Jika Anda memilih titik waktu antara 3 dan 4, maka kedua peserta terlambat untuk kereta dan dipaksa untuk menunggu yang berikutnya bersama-sama, yaitu, berlari lagi tidak efektif.

Ternyata dari 4 periode waktu konvensional, efektif untuk turun hanya jika peserta mendekati eskalator antara 2 dan 3 kali (Gbr. 4). Probabilitas untuk masuk ke dalamnya adalah 1/4. Akibatnya, di bawah kondisi tugas yang diberikan, keputusan untuk lari tidak praktis, karena peserta kedua lebih mungkin (dengan probabilitas 3/4) untuk berjalan sia-sia dan akan dipaksa untuk menunggu kereta bersama dengan yang pertama, yang turun kemudian.



Pernyataan berikut akan sepenuhnya adil:

1. Interval antara kereta bisa menurun dan meningkat. Waktu parkir dapat meningkat, dan waktu tunggu dapat menurun (dengan interval yang sama) dan sebaliknya.
2. Kecepatan eskalator turun adalah konstan, tetapi waktu penurunan dapat bervariasi, karena stasiun bisa lebih atau kurang dalam.
3. Peserta kedua mungkin berjalan dengan baik bukan 2, tetapi 3 atau bahkan 4 kali lebih cepat dari eskalator.

Untuk menilai dampak dari perubahan faktor-faktor di atas, perlu untuk mendapatkan hubungan antara nilai-nilai ini dan probabilitas untuk mendapatkan eskalator pada saat itu efektif untuk dijalankan.

Untuk melakukan ini, kami akan menggambarkan kasus lain (Gbr. 5). Kami membiarkan semua data asli tidak berubah dengan pengecualian satu: koefisien $$ naik menjadi 4. Artinya, peserta kedua akan berada di bawah 4 kali lebih cepat dari yang pertama. Untuk kenyamanan gambar, kami membagi interval kami menjadi 8 bagian yang sama. Jadi, waktu turun di eskalator sekarang sama dengan 4 segmen, kereta berhenti di dua, waktu tunggu 6, dan waktu turun untuk berjalan sendiri. Tidak sulit untuk mengetahui bahwa sekarang panjang interval waktu "efektif" (dari 4 hingga 7 poin dalam waktu) adalah 3. Artinya, probabilitas $$ sama dengan 3/8. Ini sudah lebih dari pada kasus pertama, tetapi kami tidak melakukan perubahan ini sama sekali untuk menilai probabilitas.



Berdasarkan Gambar 4 dan Gambar 5, jelas bahwa panjang segmen "efektif" adalah $$ . Membaginya dengan panjang interval dan dapatkan probabilitasnya $$ dimana $$ .
Kami melakukan serangkaian transformasi: $$$$ .
Rumus terakhir: $$ .

Berdasarkan rumus ini, beberapa kesimpulan mendasar dapat diambil sekaligus:

1. Nilai probabilitas tidak terpengaruh oleh perubahan waktu parkir dan latih waktu tunggu jika total interval tidak berubah (Gbr. 6).
   
   
   
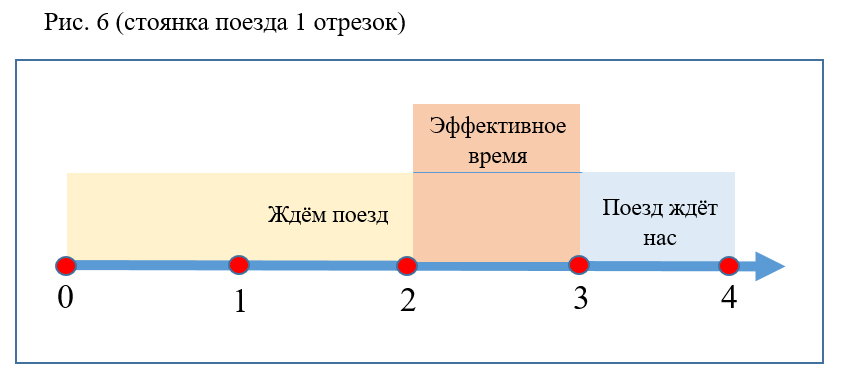
2. Semakin besar interval antara kereta, semakin rendah probabilitas P (Gbr. 7).
   
   
   
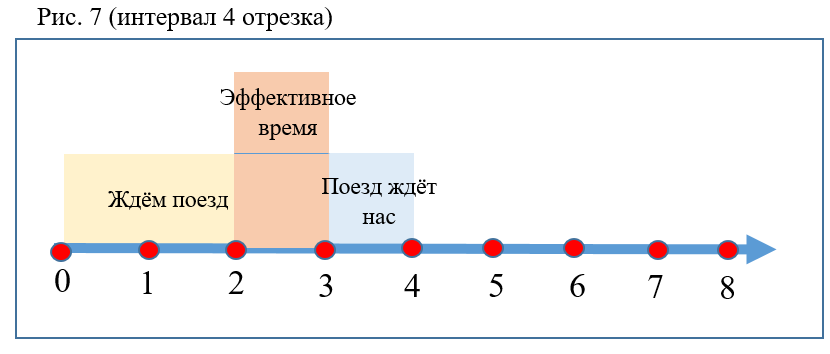
3. Probabilitas meningkat jika rasio waktu turun pada eskalator terhadap interval dan / atau koefisien K meningkat.
   

Pemeriksaan kesetiaan

Sekarang mari kita lihat seberapa benar formula turunannya?

Untuk memverifikasi kebenaran formula, kita beralih ke statistik, yang sangat berguna pada tahun 2014 oleh koresponden The Village. Saya menyatakan pengakuan saya dan, tentu saja, di akhir artikel saya akan meninggalkan tautan ke artikel asli. Juga bagus bahwa statistik disajikan sebagai infografis visual.

Eksperimen 1. Stasiun metro Chekhovskaya



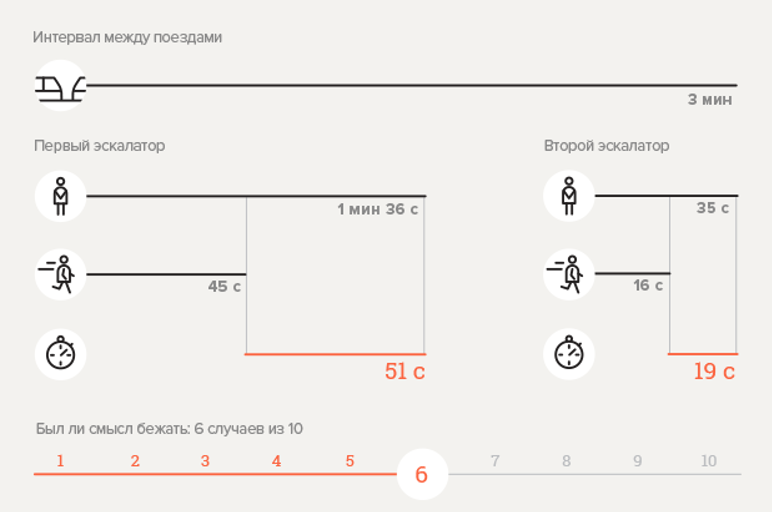
Hitung probabilitasnya $$ .
Di sini $$ ; $$ ; $$ ; $$ ; $$ .

Hasilnya diperoleh, ternyata, menyimpang dari data eksperimen. Apakah formula itu salah? Tidak! Dapat dilihat dari infografik bahwa turun ke stasiun melibatkan perjalanan dengan dua eskalator, namun, waktu transisi di antara mereka tidak diperhitungkan. Jika, untuk keandalan, kami menganggap bahwa transisi membutuhkan setidaknya 30 detik, kemudian, menggantikan nilai baru $$ kami mendapatkan: $$ ; $$ , yang jauh lebih dekat dengan hasil eksperimen. Perlu juga dicatat bahwa percobaan hanya menyediakan 10 pengulangan. Dengan meningkatkan jumlah pengulangan, dimungkinkan untuk mencapai kebetulan yang hampir lengkap dari data yang dihitung dengan hasil yang diperoleh selama percobaan.

Eksperimen 2. Stasiun Metro "Victory Park"



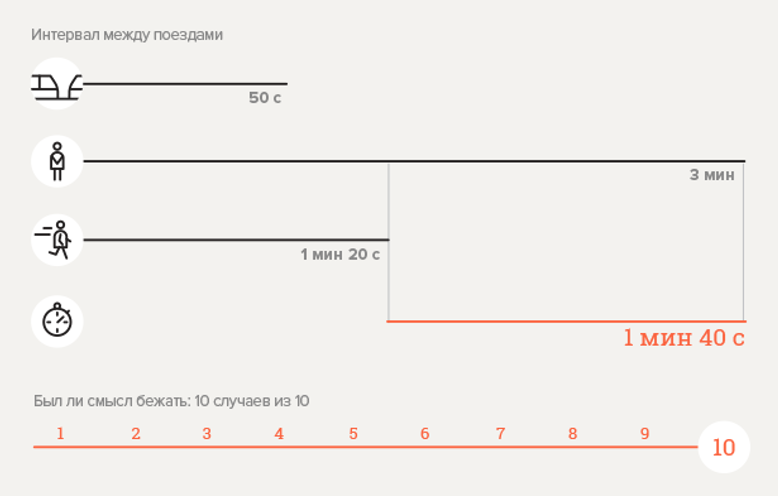
Hitung probabilitasnya $$ .
Di sini $$ ; $$ ; $$ ; $$ ; $$ .
Dapat dilihat bahwa kami mendapat probabilitas lebih besar dari satu. Tetapi tidak ada kontradiksi di sini. Jika Anda melihat bentuk umum rumus, menjadi jelas bahwa dalam kasus ketika waktu turun di eskalator sama dengan interval antar kereta, maka peningkatan kecepatan setidaknya 2 kali akan membuat probabilitas bahwa percepatan penurunan efektif sama dengan 0,5. Jika waktu perjalanan eskalator lebih besar daripada interval, maka dengan koefisien yang sama $$ kemungkinan naik kereta lebih awal hanya akan meningkat. Akhirnya, jika waktu turun di eskalator adalah 2 kali atau lebih dari interval, orang yang berlari dalam 100% kasus akan berada dalam waktu untuk kereta yang tersisa di eskalator tidak akan punya waktu untuk. Efek inilah yang kami amati dalam percobaan ini: koresponden menyimpulkan bahwa ia hanyut dalam 10 dari 10 kasus.

Eksperimen 3. Stasiun metro Park Kultury



Hitung probabilitasnya $$ .
Di sini $$ ; $$ ; $$ ; $$ ; $$ .

Lagi-lagi kesalahan? Tidak semuanya. Dapat dilihat bahwa, sebagaimana disebutkan di atas, waktu penurunan pada eskalator adalah 2 kali interval antar kereta. Waktu berlari 2 kali lebih sedikit. Ternyata setiap keturunan harus efektif. Tapi jangan lupa bahwa sebelum memulai diskusi, kami membuat asumsi tentang penutupan pintu sesaat dan setidaknya keberangkatan kereta langsung dari stasiun. Jika Anda membayangkan pilihan seperti pada Gambar 8, menjadi jelas bahwa dalam kehidupan nyata orang yang melarikan diri mungkin tidak punya waktu untuk duduk di titik 1 (misalnya, kereta akan berangkat sedikit lebih awal) dan pada titik 2 kereta, sebaliknya, akan menunda sedikit, dan kemudian orang yang tidak berlari akan duduk di dalamnya bersama orang yang terlambat berlari di kereta sebelumnya.



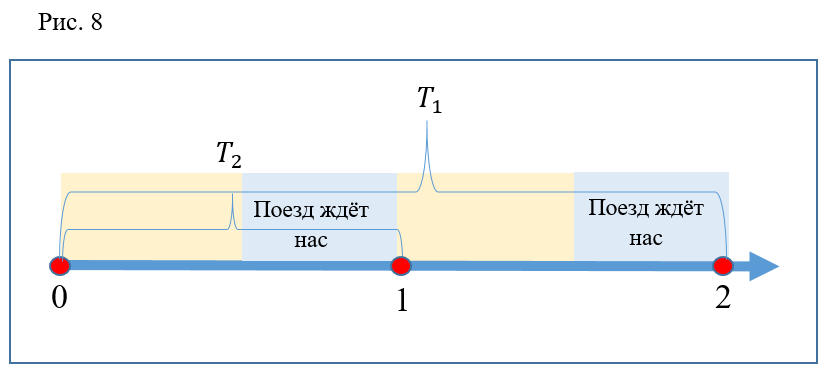
Saya kira itu di kedua kali "tidak efektif" itu terjadi. Ada setiap alasan untuk menyatakan bahwa dengan peningkatan jumlah pengulangan percobaan, persentase proses "efektif" akan cenderung 100%.

Kesimpulan

Sekarang, berdasarkan data eksperimental yang tersedia, dimungkinkan untuk mengkonfirmasi kebenaran formula, kami akan menganalisisnya dan menarik kesimpulan. Karena sejak awal kami sepakat bahwa kami akan mempertimbangkan keputusan untuk menjalankan kebijaksanaan jika probabilitas penurunan yang efektif lebih besar dari atau sama dengan 0,5. Artinya, secara harfiah, jika kita dapat memastikan bahwa setidaknya dalam setengah kasus kita akan berlari karena alasan yang baik, maka itu benar-benar layak untuk mengambil risiko dan berjalan, karena jika kita terlambat, kita praktis tidak akan kehilangan apa pun. Berdasarkan hal tersebut di atas, kami menulis ulang rumus probabilitas sebagai berikut: $$ .

Sangat menarik bahwa, seperti yang telah kita ketahui, masuk akal untuk selalu berlari ketika $$ . Pada saat yang sama, juga benar bahwa jika $$ , tidak peduli seberapa cepat Anda berlari, kemungkinan naik kereta lebih awal adalah kurang dari 0,5, karena sudah jelas itu $$ tidak akan pernah lebih besar dari atau sama dengan 1.

Sekarang mari kita lihat kecepatan koresponden. Rata-rata, ini sekitar 2 kali kecepatan eskalator (waktu penurunan 2 kali lebih sedikit). Secara umum, data ini bertepatan dengan hasil eksperimen saya sendiri (saya tidak melihat titik membawanya). Sebagai aturan, sudah sulit untuk mengembangkan kecepatan dengan koefisien K minimal 3: ada banyak orang yang ingin berlari turun di eskalator nyata dan, apalagi, orang yang berdiri di sebelah kiri mereka atau barang-barang mereka (tas, koper) dapat mengganggu. Berarti $$ , dan $$ . Artinya, keputusan untuk mempercepat hanya akan sesuai jika rasio $$ tidak kurang dari 1. Dan ini hanya mungkin terjadi ketika waktu turun di eskalator turun tidak kurang dari interval antara kereta. Di metro nyata, di mana interval rata-rata antara kereta api adalah 2 menit, tidak semua stasiun bisa membanggakan keturunan yang panjang. Sebagai aturan, bahkan di metro St. Petersburg, waktu perjalanan eskalator adalah sekitar 1 menit 30 detik, yaitu 0,75 kali lebih sedikit dari interval. Dari sini mengikuti kesimpulan mendasar yang sangat jelas dan paling penting: jika Anda tahu pasti bahwa eskalator di stasiun ini bergerak kurang dari interval antar kereta, maka tidak praktis untuk berjalan di sepanjang itu.

PS Harap perhatikan fakta bahwa tugas ini tidak memperhitungkan kebutuhan untuk masuk ke gerbong tertentu. Ini secara eksklusif tentang naik ke platform dan kemudian naik kereta.

Sumber data eksperimental: Desa . Terima kasih lagi!