Terjemahan artikel ini disiapkan khusus untuk siswa dalam kursus dasar dan lanjutan "Matematika untuk Ilmu Data".
Teorema Bayes adalah salah satu teorema statistik dan probabilitas yang paling terkenal. Bahkan jika Anda tidak bekerja dengan menghitung indikator kuantitatif, Anda mungkin harus berkenalan dengan teorema ini di beberapa titik dalam persiapan ujian.
P (A | B) = P (B | A) * P (A) / P (B)Begitulah tampilannya, tetapi apa artinya dan bagaimana cara kerjanya? Hari ini kita akan mencari tahu dan masuk jauh ke dalam teorema Bayes.
Alasan untuk mengkonfirmasi penilaian kami
Apa inti dari teori probabilitas dan statistik? Salah satu kegunaan paling penting terkait dengan pengambilan keputusan di bawah ketidakpastian. Ketika Anda memutuskan untuk melakukan tindakan apa pun (kecuali, tentu saja, Anda adalah orang yang masuk akal), Anda bertaruh bahwa setelah menyelesaikan tindakan ini akan menghasilkan hasil yang lebih baik daripada jika tindakan ini tidak terjadi ... Tetapi bertaruh adalah sesuatu tidak dapat diandalkan, bagaimana Anda akhirnya memutuskan apakah akan mengambil langkah ini atau itu atau tidak?
Dengan satu atau lain cara, Anda mengevaluasi probabilitas hasil yang sukses, dan jika probabilitas ini di atas nilai ambang tertentu, Anda mengambil langkah.
Dengan demikian, kemampuan untuk secara akurat menilai kemungkinan sukses sangat penting untuk membuat keputusan yang tepat. Terlepas dari kenyataan bahwa keacakan akan selalu berperan dalam hasil akhir, Anda harus belajar untuk menggunakan keacakan ini dengan benar dan mengubahnya menjadi keuntungan Anda seiring waktu.
Di sinilah teorema Bayes mulai berlaku - teorema ini memberi kita dasar kuantitatif untuk mempertahankan keyakinan kita pada hasil suatu tindakan ketika faktor lingkungan berubah, yang, pada gilirannya, memungkinkan kita untuk meningkatkan proses pengambilan keputusan dari waktu ke waktu.
Mari kita menganalisis rumusnya
Mari kita lihat rumusnya lagi:
P (A | B) = P (B | A) * P (A) / P (B)Di sini:
- P (A | B) - probabilitas terjadinya peristiwa A, asalkan peristiwa B telah terjadi;
- P (B | A) - probabilitas terjadinya peristiwa B, asalkan peristiwa A telah terjadi. Sekarang sepertinya semacam lingkaran setan, tetapi kita akan segera mengerti mengapa formula ini bekerja;
- P (A) - probabilitas apriori (tanpa syarat) untuk terjadinya peristiwa A;
- P (B) - probabilitas apriori (tanpa syarat) dari kejadian B.
P (A | B) adalah contoh probabilitas posteriori (bersyarat), yaitu, yang mengukur probabilitas keadaan tertentu dari dunia sekitarnya (yaitu, keadaan di mana peristiwa B terjadi). Sedangkan P (A) adalah contoh probabilitas apriori, yang dapat diukur di setiap negara di dunia sekitarnya.
Mari kita lihat teorema Bayes yang sedang beraksi sebagai contoh. Misalkan Anda baru saja menyelesaikan kursus analisis data dari bootcamp. Anda belum menerima tanggapan dari beberapa perusahaan tempat Anda diwawancarai, dan mulai khawatir. Jadi, Anda ingin menghitung kemungkinan bahwa perusahaan tertentu akan membuat Anda menawarkan pekerjaan, asalkan tiga hari telah berlalu dan mereka belum menghubungi Anda kembali.
Kami menulis ulang rumus dalam contoh kami. Dalam hal ini, hasil A (
Penawaran ) menerima tawaran pekerjaan, dan hasil B (
NoCall ) adalah "tidak ada panggilan telepon selama tiga hari." Berdasarkan ini, rumus kami dapat ditulis ulang sebagai berikut:
P ( Penawaran | NoCall ) = P ( NoCall | Penawaran ) * P ( Penawaran ) / P ( NoCall )Nilai
P ( Penawaran | NoCall ) adalah probabilitas untuk menerima penawaran, asalkan tidak ada panggilan dalam waktu tiga hari. Probabilitas ini sangat sulit untuk dinilai.
Namun, probabilitas kebalikannya,
P ( NoCall | Offer ) , yaitu, tidak adanya panggilan telepon selama tiga hari, mengingat bahwa pada akhirnya Anda menerima tawaran pekerjaan dari perusahaan, sangat mungkin untuk melampirkan beberapa nilai. Dari percakapan dengan teman, perekrut dan konsultan, Anda akan menemukan bahwa probabilitas ini kecil, tetapi kadang-kadang perusahaan masih bisa tetap diam selama tiga hari jika masih berencana untuk mengundang Anda untuk bekerja. Jadi Anda mengevaluasi:
P ( NoCall | Penawaran ) = 40%40% tidak buruk dan sepertinya masih ada harapan! Tapi kita belum selesai. Sekarang kita perlu mengevaluasi
P ( Penawaran ) , kemungkinan pergi bekerja. Semua orang tahu bahwa mencari pekerjaan adalah proses yang panjang dan sulit, dan Anda mungkin harus melalui wawancara beberapa kali sebelum Anda menerima tawaran ini, jadi Anda mengevaluasi:
P ( Penawaran ) = 20%Sekarang kita hanya perlu mengevaluasi
P ( NoCall ) , kemungkinan Anda tidak akan menerima panggilan dari perusahaan dalam waktu tiga hari. Ada banyak alasan mengapa Anda mungkin tidak dipanggil kembali dalam tiga hari - mereka mungkin menolak pencalonan Anda atau masih melakukan wawancara dengan kandidat lain, atau perekrut sedang sakit dan karena itu tidak menelepon. Nah, ada banyak alasan mengapa Anda mungkin tidak memiliki panggilan, sehingga Anda menilai probabilitas ini sebagai:
P ( NoCall ) = 90%Dan sekarang, dengan menggabungkan semuanya, kita dapat menghitung
P ( Penawaran | NoCall ) :
P ( Penawaran | NoCall ) = 40% * 20% / 90% = 8,9%Ini cukup kecil, jadi, sayangnya, lebih rasional untuk meninggalkan harapan untuk perusahaan ini (dan terus mengirim resume ke orang lain). Jika masih terlihat agak abstrak, jangan khawatir. Saya merasakan hal yang sama ketika pertama kali belajar tentang teorema Bayes. Sekarang mari kita lihat bagaimana kita mencapai 8,9% ini (perlu diingat bahwa skor awal 20% Anda sudah rendah).
Intuisi di balik formula
Ingat, kami mengatakan bahwa teorema Bayesian memberikan dasar untuk konfirmasi penilaian kami? Jadi dari mana asalnya? Mereka diambil dari probabilitas a priori
P (A) , yang dalam contoh kita disebut
P ( Penawaran ) , pada kenyataannya, ini adalah penilaian awal kita tentang seberapa besar kemungkinan seseorang akan menerima tawaran pekerjaan. Dalam contoh kami, Anda dapat mengasumsikan bahwa probabilitas apriori adalah probabilitas bahwa Anda akan menerima tawaran pekerjaan pada saat Anda meninggalkan wawancara.
Informasi baru muncul - 3 hari telah berlalu, dan perusahaan tidak menghubungi Anda kembali. Jadi, kita menggunakan bagian lain dari persamaan untuk menyesuaikan probabilitas a priori kita dari suatu peristiwa baru.
Mari kita lihat probabilitas
P (B | A) , yang dalam contoh kita disebut
P ( NoCall | Offer ) . Ketika pertama kali melihat teorema Bayes, Anda bertanya pada diri sendiri: Bagaimana Anda tahu di mana mendapatkan probabilitas
P (B | A) ? Jika saya tidak tahu berapa probabilitas
P (A | B) , lalu seberapa ajaib saya harus tahu berapa probabilitas
P (B | A) ? Saya ingat ungkapan yang pernah dikatakan
Charles Munger :
"Balik, selalu balik!"
- Charles Munger
Maksudnya ketika Anda mencoba menyelesaikan masalah yang sulit, Anda harus membalikkannya dan melihatnya dari sudut yang berbeda. Inilah yang dilakukan oleh teorema Bayes. Mari kita merumuskan kembali teorema Bayes dalam hal statistik untuk membuatnya lebih dimengerti (saya belajar tentang ini
dari sini ):
Bagi saya, misalnya, catatan seperti itu terlihat lebih jelas. Kami memiliki hipotesis a priori (Hipotesis) - bahwa kami mendapat pekerjaan, dan fakta yang dapat diamati - bukti (Bukti) - tidak ada panggilan telepon selama tiga hari. Sekarang kita ingin mengetahui kemungkinan hipotesis kita benar, dengan mempertimbangkan fakta-fakta yang disajikan. Seperti yang diputuskan di atas, kami memiliki probabilitas
P (A) = 20% .
Saatnya membalikkan segalanya! Kami menggunakan
P ( Bukti | Hipotesis ) untuk melihat masalah dari sisi lain dan bertanya: "Berapa probabilitas kejadian bukti ini terjadi di dunia di mana hipotesis kami benar?" Jadi, jika kita kembali ke contoh kita, kita ingin tahu seberapa besar kemungkinannya jika mereka tidak menghubungi kita dalam tiga hari, kita masih akan dipekerjakan. Pada gambar di atas, saya menandai
P ( Bukti | Hipotesis ) sebagai "scaler" (scaler), karena kata ini mencerminkan esensi dari makna dengan baik. Ketika kita mengalikannya dengan nilai a priori, itu mengurangi atau meningkatkan probabilitas suatu peristiwa, tergantung pada apakah ada peristiwa yang membuktikan hipotesis kita "berbahaya". Dalam kasus kami, semakin banyak hari berlalu tanpa panggilan, semakin kecil kemungkinan kami akan dipanggil untuk bekerja. 3 hari keheningan sudah buruk (mereka mengurangi probabilitas a priori kami sebesar 60%), sementara 20 hari tanpa panggilan akan benar-benar menghancurkan harapan mendapatkan pekerjaan. Dengan demikian, semakin banyak bukti yang terakumulasi (semakin banyak hari berlalu tanpa panggilan telepon), semakin cepat scaler mengurangi kemungkinan. Scaler adalah mekanisme yang digunakan teorema Bayes untuk menyesuaikan penilaian kita.
Ada satu hal yang saya perjuangkan dengan versi asli artikel ini. Ini adalah rumusan mengapa
P ( Bukti | Hipotesis ) lebih mudah untuk dievaluasi daripada P (Hipotesis | Bukti). Alasan untuk ini adalah bahwa
P ( Evidence | Hypothesis ) adalah area penilaian yang jauh lebih terbatas tentang dunia. Mempersempit ruang lingkup, kami menyederhanakan tugas. Kita dapat menggambar analogi dengan api dan asap, di mana api adalah hipotesis kami, dan pengamatan asap adalah peristiwa yang membuktikan keberadaan api.
P (api | asap) lebih sulit dievaluasi, karena banyak hal dapat menyebabkan asap - knalpot mobil, pabrik, orang yang menggoreng hamburger dengan arang. Pada saat yang sama,
P (smoke | fire) lebih mudah untuk dievaluasi, karena di dunia di mana ada api, hampir pasti akan ada asap.
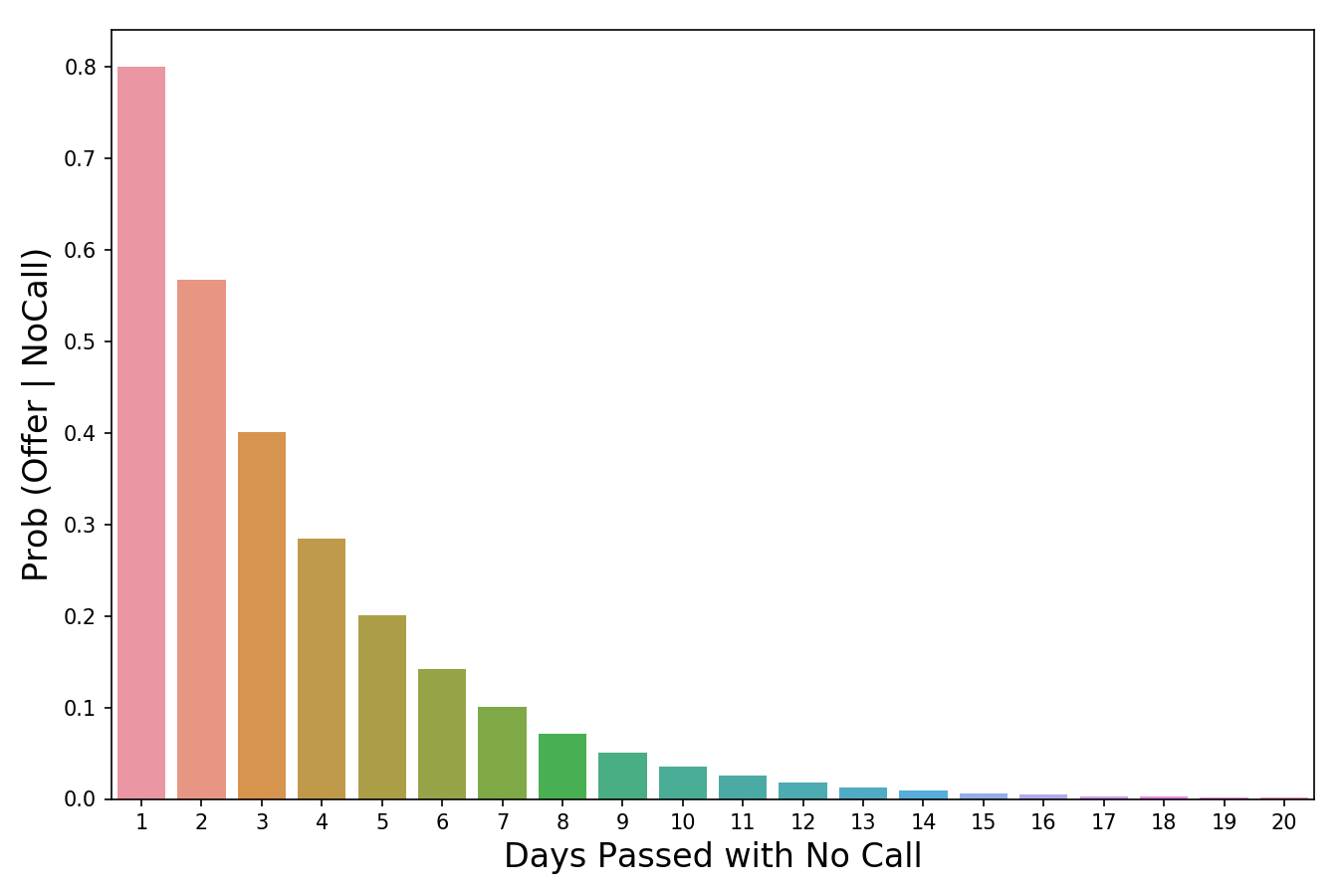Nilai probabilitas berkurang ketika jumlah hari berlalu tanpa panggilan.Bagian terakhir dari rumus,
P (B) atau
P ( Bukti ) , adalah normalizer. Seperti namanya, tujuannya adalah untuk menormalkan produk probabilitas dan scaler priori. Jika tidak ada normalizer, kami akan memiliki ekspresi berikut:
Perhatikan bahwa produk probabilitas apriori dan scaler sama dengan probabilitas gabungan. Dan karena salah satu komponen
P ( Bukti ) di dalamnya , maka probabilitas gabungan akan dipengaruhi oleh frekuensi kejadian yang kecil.
Ini adalah masalah karena probabilitas bersama adalah nilai yang mencakup semua negara di dunia. Tapi kami tidak membutuhkan semua negara bagian, kami hanya membutuhkan negara-negara yang dikonfirmasi oleh peristiwa-bukti. Dengan kata lain, kita hidup di dunia di mana peristiwa - bukti telah terjadi, dan jumlahnya tidak penting lagi (karena itu, kita tidak ingin mereka mempengaruhi perhitungan kita secara prinsip). Membagi produk dari probabilitas apriori dan scaler dengan
P ( Bukti ) mengubahnya dari probabilitas bersama menjadi bersyarat (posterior). Probabilitas kondisional hanya memperhitungkan keadaan dunia di mana peristiwa-bukti terjadi, yang persis apa yang kita capai.
Sudut pandang lain dari mana kita dapat melihat mengapa kita membagi scaler menjadi normalizer adalah bahwa mereka menjawab dua pertanyaan penting - dan sikap mereka menggabungkan informasi ini. Mari kita ambil contoh dari
artikel Bayes saya yang terbaru. Misalkan kita mencoba mencari tahu apakah hewan yang diamati adalah kucing, berdasarkan pada tanda tunggal - ketangkasan. Yang kita tahu adalah hewan yang kita bicarakan itu gesit.
- Scaler memberi tahu kami berapa persen kucing bagus dengan ketangkasan. Nilai ini harus cukup tinggi, katakanlah 0,90.
- Penormalisasi memberi tahu kita berapa persen dari perangkap binatang pada prinsipnya. Nilai ini harus rata-rata, katakanlah 0,50.
- Rasio 0,90 / 0,50 = 1,8 menunjukkan bahwa Anda perlu mengubah probabilitas a priori, karena jika sebelumnya Anda berpikir sebaliknya, inilah saatnya untuk mengubah pikiran, karena kemungkinan besar Anda berurusan dengan kucing. Alasan mengapa hal ini dapat dipikirkan adalah karena kami mengamati beberapa bukti bahwa hewan itu gesit. Kemudian kami menemukan bahwa proporsi kucing tangkas lebih besar daripada proporsi hewan tangkas pada umumnya. Mempertimbangkan bahwa saat ini kita hanya tahu sepotong bukti dan tidak lebih dari itu, akan bijaksana untuk mempertimbangkan kembali kepercayaan kita ke arah pemikiran bahwa kita masih memperhatikan kucing.
Untuk meringkas
Sekarang kita tahu bagaimana menafsirkan setiap bagian dari rumus, kita akhirnya bisa menyatukan semuanya dan melihat apa yang terjadi:
- Segera setelah wawancara, kami menetapkan probabilitas apriori - peluang bahwa kami akan dipekerjakan adalah 20%.
- Semakin banyak hari yang berlalu tanpa panggilan, semakin kecil kemungkinannya kita akan dipekerjakan. Misalnya, setelah tiga hari tanpa panggilan, kami percaya bahwa di dunia di mana kami bisa mendapatkan pekerjaan ini, hanya ada 40% peluang bahwa perusahaan akan menarik begitu lama sebelum ia memanggil Anda. Lipat gandakan scaler dengan probabilitas apriori dan dapatkan 20% * 40% = 8%
- Akhirnya, kami memahami bahwa 8% dihitung untuk semua kondisi di mana dunia berada. Tetapi kami hanya mengkhawatirkan kondisi di mana kami belum dipanggil selama tiga hari. Untuk hanya bekerja dengan kondisi ini, kami mengambil probabilitas a priori sebesar 90% bahwa tidak akan ada panggilan dalam tiga hari dan kami mendapatkan normalizer. Kami membagi 8% yang sebelumnya diterima oleh normalizer 8% / 90% = 8,9% dan mendapatkan jawaban akhir. Total, dalam semua kondisi dunia, jika Anda belum menerima panggilan dari perusahaan dalam waktu tiga hari, kemungkinan mendapatkan pekerjaan hanya 8,9%.
Saya harap artikel ini bermanfaat bagi Anda!