VK memiliki grup dengan uraian berikut:

Foto yang sama disimpan secara manual setiap hari ke komputer dan diunggah lagi, secara bertahap kehilangan kualitas.

Di sebelah kiri adalah gambar asli yang diunggah pada 7 Juni 2012, di sebelah kanan adalah seperti sekarang.

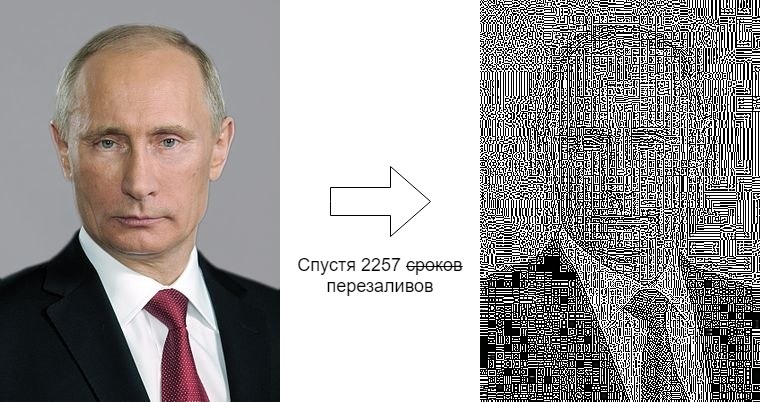
Perbedaan ini sangat mencurigakan. Mari kita coba mencari tahu apa yang terjadi selama 7 tahun ini. Untuk kenalan ada artikel tentang Medusa tentang grup ini, tetapi hanya sisi teknis yang akan menarik perhatian kita.

Mengapa dan pada tahap apa JPEG menekan dengan kerugian

Pertimbangkan skema penyandian dan penguraian JPEG yang sangat disederhanakan. Hanya operasi-operasi itu yang diperlihatkan yang menggambarkan prinsip-prinsip dasar dari algoritma JPEG.

Jadi, 4 operasi:

• DCT adalah transformasi kosinus diskrit.
• Kuantisasi - membulatkan setiap nilai ke kelipatan terdekat dari langkah kuantisasi: y = [x / h] * h, di mana h adalah langkah.
• IDCT adalah transformasi cosinus diskrit terbalik.
• Pembulatan adalah pembulatan normal. Tahap ini tidak dapat ditampilkan dalam diagram, karena jelas. Tetapi kemudian pentingnya akan ditunjukkan.

Warna hijau menunjukkan operasi yang menyimpan semua informasi (tanpa memperhitungkan kerugian saat bekerja dengan angka floating point), yang berwarna merah muda - hilang. Yaitu, kerugian dan artefak muncul bukan karena transformasi cosinus, tetapi karena kuantisasi sederhana. Artikel ini tidak akan mempertimbangkan tahap penting - pengkodean Huffman, karena dilakukan tanpa kerugian.

Pertimbangkan langkah-langkah ini secara lebih rinci.

DCT

Karena ada beberapa variasi DCT, untuk berjaga-jaga, saya akan menjelaskan bahwa JPEG menggunakan tipe kedua DCT dengan normalisasi. Saat menyandikan, setiap gambar dibagi menjadi 8x8 kotak (untuk setiap saluran). Setiap kotak seperti itu dapat direpresentasikan sebagai vektor 64 dimensi. Transformasi kosinus adalah untuk menemukan koordinat vektor ini dalam basis ortonormal lain. Sulit untuk memvisualisasikan ruang 64 dimensi, jadi analogi 2 dimensi akan diberikan di bawah ini. Anda dapat membayangkan bahwa gambar dibagi menjadi 2x1 blok. Dalam grafik yang akan ditampilkan di bawah ini, sumbu x sesuai dengan nilai-nilai piksel pertama dari blok, sumbu y ke yang kedua.

Melanjutkan analogi dengan contoh spesifik, anggaplah bahwa nilai dua piksel dari gambar asli adalah 3 dan 4. Gambarlah vektor (3, 4) dengan dasar aslinya, seperti yang ditunjukkan pada gambar di bawah ini. Dasar aslinya ditandai dengan warna biru. Koordinat vektor dalam beberapa basis baru adalah (4.8, 1.4).

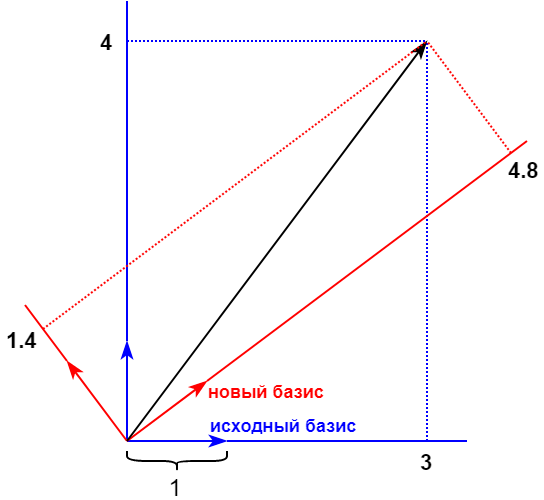
Dalam contoh yang dipertimbangkan, basis baru dipilih secara acak. DCT menawarkan dasar tetap 64-dimensi yang sangat spesifik. Pembenaran mengapa ini digunakan dalam JPEG sangat menarik, dan dijelaskan oleh saya di artikel lain. Kami hanya akan menyentuh intinya. Secara umum, nilai semua piksel adalah setara. Tetapi jika kita mengonversinya menggunakan DCT, maka dari 64 koordinat yang dihasilkan dalam basis baru (disebut koefisien transformasi DCT), kita dapat dengan aman memundurkan atau sekitar beberapa dari mereka, dengan kerugian minimal. Ini dimungkinkan berkat fitur gambar yang dapat dikompres.

Kuantisasi

Nilai pecahan tidak dapat disimpan dalam file. Oleh karena itu, tergantung pada langkah kuantisasi, nilai 4.8, 1.4 akan disimpan sebagai berikut:

• pada langkah 1 (opsi paling lembut): 5 dan 1,
• pada langkah 2: 4 dan 2,
• pada langkah 3: 6 dan 0.

Biasanya langkah yang dipilih berbeda untuk setiap nilai. File JPEG memiliki setidaknya satu larik, yang disebut tabel kuantisasi, yang menyimpan 64 langkah kuantisasi. Tabel ini tergantung pada kualitas kompresi yang diatur dalam editor grafis apa pun.

IDCT

Sama seperti DCT, tetapi dengan basis yang dialihkan. Secara matematis, x = IDCT (DCT (x)), jadi jika tidak ada kuantisasi, maka akan mungkin untuk memulihkan tanpa kehilangan. Tetapi tidak akan ada kompresi. Karena penggunaan kuantisasi, vektor asli tidak selalu dapat dihitung secara akurat. Gambar berikut menunjukkan 2 contoh dengan pemulihan yang akurat dan tidak akurat. Kisi miring sesuai dengan basis baru, garis lurus ke yang asli.

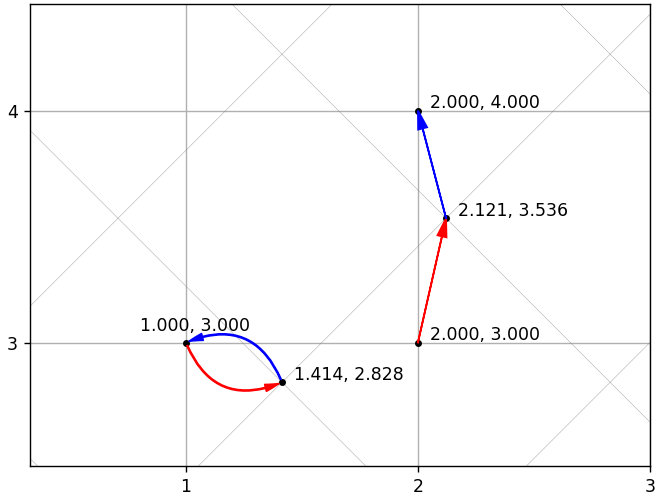
Pertanyaan yang jelas muncul: dapatkah urutan transcoding mengarah ke vektor yang sangat berbeda dari aslinya? Mungkin

Akan menarik untuk memilah-milah semua vektor integer dan melihat apa yang akan menyebabkan transcoding mereka. Untuk mengurangi kebisingan informasi, kami menghapus kisi-kisi dasar awal dan kami akan langsung menghubungkan vektor asli dan yang direkonstruksi (tanpa langkah perantara) dengan segmen. Pertama, pertimbangkan langkah kuantisasi sama dengan 1 untuk semua koordinat. Basis baru pada gambar berikut diputar 45 derajat dan untuk itu kami memiliki 17,1% dari pemulihan yang tidak akurat. Warna segmen tidak berarti apa-apa, tetapi mereka akan berguna untuk mencegah penggabungan visual mereka.

Dasar ini adalah 10,3 derajat dengan pemulihan 7,4% tidak akurat:

Dekat:

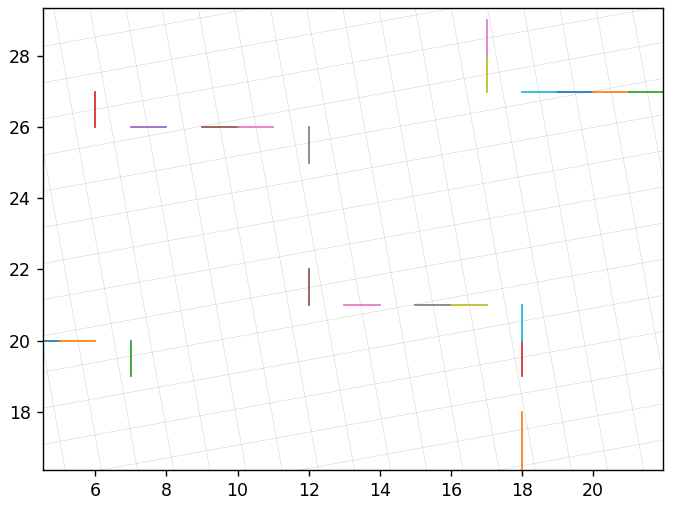
Dan yang ini di 10.4 dari 6.4%:

19 derajat dari 12,5%:

Tetapi jika Anda mengatur langkah kuantisasi lebih besar dari 1, maka vektor yang direkonstruksi mulai dengan jelas berkonsentrasi dekat dengan node grid. Ini adalah langkah 5:

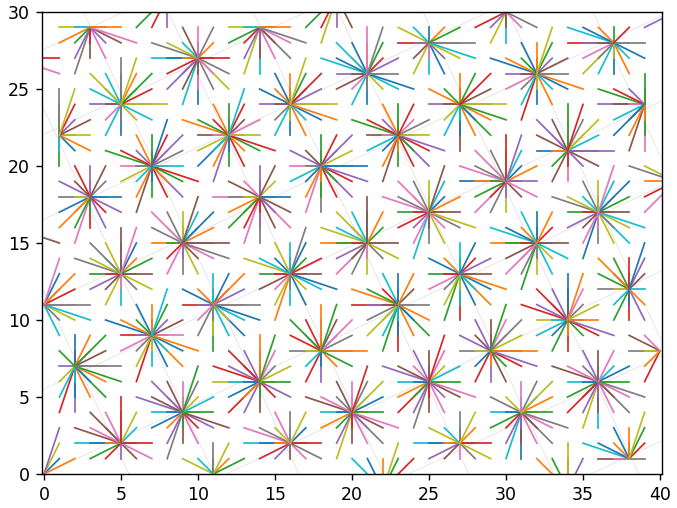
Ini 2:

Jika Anda mengkode ulang gambar beberapa kali, tetapi dengan nada yang sama, maka hampir tidak ada yang terjadi dibandingkan dengan pengodean ulang tunggal. Nilai-nilai tampaknya "terjebak" di node grid dan tidak bisa lagi "melompat" dari sana ke node lain. Jika langkahnya berbeda, maka vektor akan "melompat" dari satu simpul kisi ke yang lain. Ini bisa membawanya ke mana saja. Gambar berikut menunjukkan hasil 4 transkode dengan langkah 1, 2, 3, 4. Anda dapat melihat kisi besar dengan langkah 12. Nilai ini adalah kelipatan umum terkecil dari 1, 2, 3, 4.

Dan pada ini - dengan langkah-langkah dari 1 hingga 7. Visualisasi ditampilkan hanya untuk bagian dari vektor asli untuk meningkatkan visualisasi.

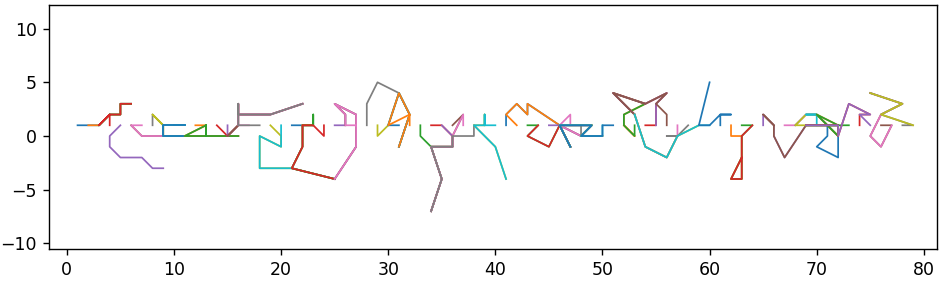
Pembulatan

Mengapa melengkapi nilai setelah IDCT? Lagipula, jika Anda menyingkirkan tahap ini, maka gambar yang dipulihkan akan diwakili oleh nilai fraksional, dan kami tidak akan kehilangan apa pun saat melakukan penyandian ulang. Dari sudut pandang matematika, kita hanya akan berpindah dari satu basis ke basis lainnya tanpa kehilangan. Perlu disebutkan di sini konversi ruang warna. Meskipun JPEG tidak mengatur ruang warna dan memungkinkan Anda untuk menyimpan langsung dalam sumber RGB, tetapi dalam sebagian besar kasus, konversi awal ke YCbCr digunakan. Fitur mata dan semua itu. Dan konversi semacam itu juga menyebabkan kerugian.

Misalkan kita mendapatkan file JPEG yang dikompres dengan kualitas maksimum, yaitu, dengan langkah kuantisasi 1 untuk semua koefisien. Kita tidak tahu codec mana yang digunakan, tetapi biasanya codec melakukan pembulatan setelah konversi RGB -> YCbCr. Karena kualitasnya maksimum, setelah IDCT kami mendapatkan nilai fraksional, tetapi agak mendekati nilai aslinya di ruang YCbCr. Jika kita berputar, maka sebagian besar dari mereka akan dipulihkan dengan tepat.

Tetapi jika tidak bulat, maka karena perbedaan kecil seperti itu, konversi YCbCr -> RGB bahkan dapat semakin menjauhkan mereka dari nilai-nilai asli. Dengan transcoding berikutnya, kesenjangan akan meningkat semakin banyak. Untuk memvisualisasikan proses ini, kami menggunakan metode komponen utama untuk memproyeksikan vektor 64-dimensi ke dalam bidang. Kemudian untuk 1000 transkode, kami mendapatkan kira-kira urutan perubahan berikut:

Nilai absolut dari sumbu di sini tidak masuk akal, tetapi signifikansi relatif dari distorsi dapat digunakan.

Beberapa Contoh Transcoding

Sumber kucing:

Setelah satu pemeliharaan ulang dengan kualitas 50:

Setelah jumlah transkode berikutnya dengan kualitas yang sama, gambar tidak berubah. Sekarang kita akan secara bertahap mengurangi kualitas dari 90 menjadi 50 dalam 1:

Tentang hal yang sama terjadi pada bagan di bawah ini:

Setelah satu pemeliharaan ulang dengan kualitas 20:

Dari 90 hingga 20:

Sekarang 1000 kali dengan kualitas acak dari 80 hingga 90:

10.000 kali:

Analisis Gambar Grup VK

Mari kita mulai analisis lebih dari 2000 gambar dari grup VK. Pertama, periksa rata-rata deviasi absolut dari awal. Sumbu x adalah nomor gambar (atau hari), sumbu y adalah penyimpangan.

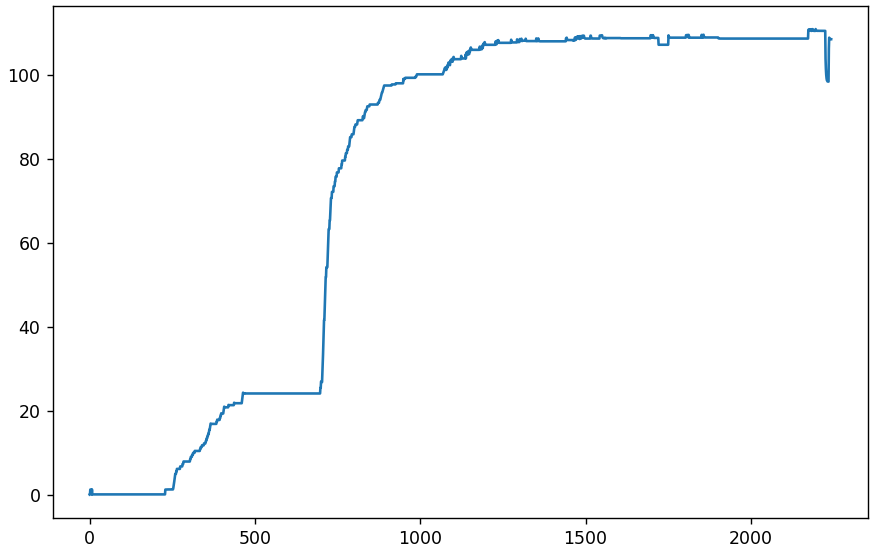
Mari kita beralih ke grafik diferensial yang menunjukkan rata-rata deviasi absolut dari gambar tetangga.

Fluktuasi kecil pada awalnya adalah normal. Sampai tanggal 232, semuanya berjalan dengan baik, gambar-gambarnya benar-benar identik. Dan tanggal 233 tiba-tiba berbeda dengan rata-rata 1,23 untuk setiap piksel (pada skala dari 0 hingga 255). Ini banyak sekali. Mungkin tabel kuantisasi baru saja berubah. Lihat itu. Dan pada saat yang sama, itu sebanding dengan ukuran file yang diterima.

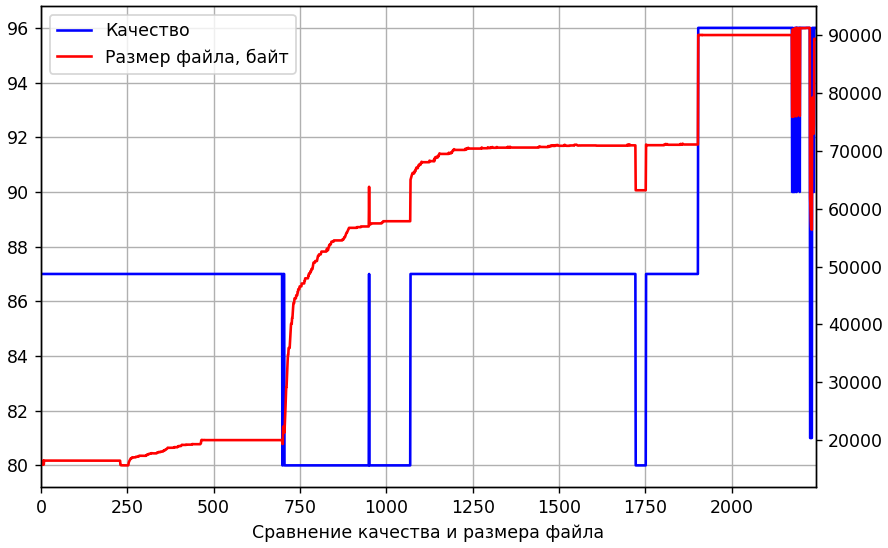
Ya, tabel telah berubah. Tapi tidak lebih awal dari tahun 700-an. Kemudian, mungkin, transcoding tersembunyi antara dengan kualitas rendah terjadi. Mari kita coba untuk menyandikan ulang 232 kali. Untuk pertama kalinya, kita akan melalui tingkat kualitas yang berbeda, dan untuk yang kedua kita menggunakan tabel kuantisasi yang sama untuk semua dari 1 hingga 700-an. Tujuan kami adalah untuk mendapatkan gambar semirip mungkin dengan yang ke-233. Pada gambar berikut, sepanjang sumbu x adalah kualitas transcoding perantara, sepanjang y adalah penyimpangan absolut rata-rata dari 233.

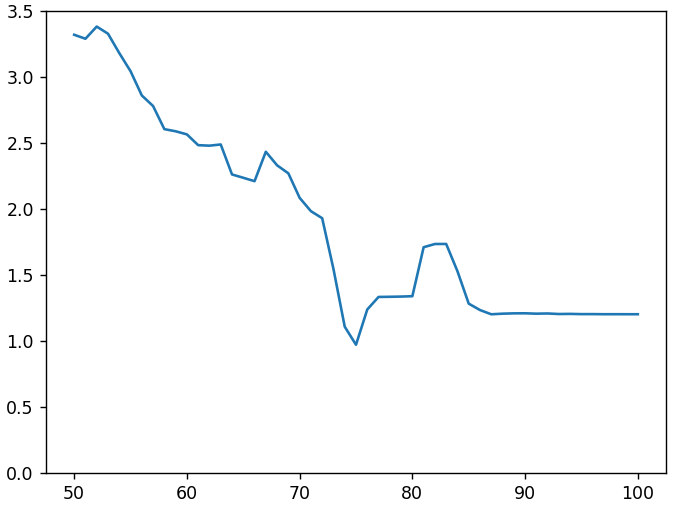
Meskipun ada kegagalan pada grafik dengan kualitas 75%, kira-kira sama dengan 1, tetapi masih jauh dari nol yang diinginkan. Menambahkan tahap menengah ke-2 dan mengubah parameter subsampling tidak memperbaiki situasi.

Dengan sisa gambar, semuanya hampir sama, ditambah perubahan dalam tabel kuantisasi juga ditumpangkan. Artinya, pada titik tertentu, gambar berubah secara dramatis, kemudian stabil dalam beberapa hari, tetapi hanya sampai lonjakan baru terjadi. Mungkin ada perubahan pada gambar itu sendiri di server. Saya tidak dapat sepenuhnya mengecualikan keterlibatan administrator grup.

Sayangnya, saya tidak mengetahui apa yang sebenarnya terjadi dengan gambar tersebut. Setidaknya sekarang saya yakin itu bukan hanya pelestarian kembali. Tetapi, yang paling penting, menjadi lebih baik untuk mewakili proses yang sedang berlangsung selama encoding dan decoding. Semoga kamu juga.

Arsipkan dengan gambar , untuk penelitian independen.