Splines dalam grafik 3d, opsi paling otomatis

Sekitar sebulan yang lalu, saya mulai belajar Python dari buku Dawson dan bangun dalam proses menulis permainan saya di bawah pygame. TK sedemikian rupa sehingga tampak paling menjanjikan untuk membuat game dengan grafis pseudo-tiga dimensi dengan memasukkan permukaan spline 3d yang tersimpan menjadi sprite. Saya akan menulis tentang yang terakhir.

Jadi, ada poligon (paling mudah untuk bekerja dengan segi empat) di mana kami ingin meregangkan permukaan kubik sehingga mereka cocok bersama dengan sangat lancar - permukaan ini adalah splines.



Paling mudah menyajikan spline untuk satu poligon sebagai fungsi

$$

$$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1)$$

Di sini

$$

$$g_1, g_2, g_3, g_4$$

- polinomial kubik yang memenuhi beberapa kondisi batas (pada gambar di bawah ini - kurva hijau dan merah muda, dan kondisi turunan-awal - vektor lilac dan biru); u dan v bervariasi dari 0 hingga 1.



Dalam interpretasi ini, beberapa derajat hilang (produk dari 2 dan 3 derajat parameter), tetapi koefisien polinom dapat ditemukan dengan menetapkan hanya 12 vektor kondisi awal (4 titik poligon dan vektor turunan sehubungan dengan u dan v untuk setiap titik). Pada persimpangan, splines bertepatan jika kondisi awal yang sama ditetapkan untuk poligon tetangga (vektor turunan haruslah collinear, permukaan melewati titik-titik yang sama dari poligon).

Satu masalah - turunan dengan pernyataan masalah seperti itu di seluruh perbatasan mungkin tidak bersamaan - akan ada artefak kecil di persimpangan. Anda dapat memikirkan 4 kondisi lagi untuk memperbaikinya dan dengan hati-hati menambahkan istilah lain ke rumus

$$

$$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$$

yang tidak merusak perbatasan, tetapi ini adalah topik untuk artikel terpisah.

Alternatif adalah permukaan Bezier , tetapi ia mengusulkan untuk menetapkan 16 parameter makna matematika yang tidak dapat dipahami (bagi saya), yaitu diasumsikan bahwa artis akan bekerja dengan tangannya sendiri. Ini tidak cocok untuk saya, jadi sepeda dengan kruk mengikuti.

Koefisien (1) paling mudah dihitung dengan mencari matriks invers ke matriks nilai dan turunannya di sudut-sudut dan mengalikannya dengan kondisi input (tiga kali, untuk setiap koordinat). Matriksnya mungkin seperti ini:


NumPy melakukan tugasnya dengan sangat baik.

Masih ada satu pertanyaan - di mana mendapatkan vektor turunan. Diasumsikan bahwa mereka entah bagaimana harus dipilih berdasarkan posisi titik tetangga (untuk poligon) dan untuk alasan kelancaran.
Bagi saya pribadi, itu masih sepenuhnya berlawanan dengan intuisi bagaimana menangani panjang vektor turunan. Arahnya bisa dimengerti, tapi panjangnya?

Alhasil, algoritma berikut ini lahir:

1. Pada tahap pertama, beberapa klasifikasi poin terjadi. Dalam grafik (titik-titik mana dari poligon dan koneksinya menentukan), siklus dengan panjang 4 dicari dan disimpan, dan di samping itu, tetangga yang paling cocok untuk peran memperpanjang tepi poligon dicatat (ditentukan terlebih dahulu tepi mana yang sesuai dengan perubahan pada parameter u dan yang sesuai dengan v). Berikut adalah sepotong kode yang mencari, mengurutkan, dan mengingat tetangga untuk titik ke-0 dari sebuah siklus:


Selanjutnya, ketika membangun spline, turunan di sepanjang tepi (misalnya, berkenaan dengan parameter u) pada titik poligon dipilih berdasarkan lokasi dua titik tepi dan satu titik yang berdekatan (biarkan itu menjadi titik vec1, vec2 dan vec3; titik di mana turunan dicari adalah yang kedua).



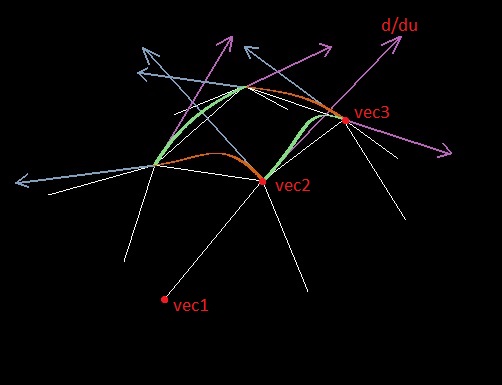
Pada awalnya saya mencoba menggunakan vektor dinormalisasi vec3 - vec1 (seperti saya menerapkan teorema Lagrange) untuk peran ini, tetapi masalah muncul justru dengan panjang vektor turunan - membuatnya konstan adalah ide yang buruk.

Penyimpangan lirik:

Untuk ilustrasi kecil tentang apa vektor turunan dalam versi parametrik, kita beralih ke analogi dua dimensi sederhana - di sini adalah sepotong busur melingkar:

$$

$$g (u) = (Rsin (u \ pi / 2), Rcos (u \ pi / 2))$$

$$

$$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$$

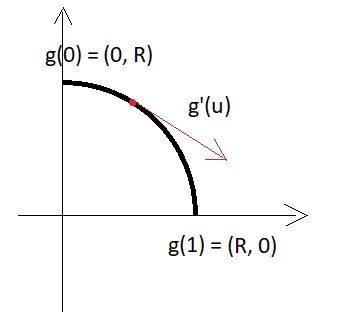
Yaitu modulus turunan = R * pi / 2 dan, secara umum, tergantung pada ukuran potongan busur, yang kami atur melalui parameter.

Apa yang harus dilakukan dengan itu sekarang? Leo Nikolaevich Tolstoy mewariskan kepada kita bahwa semuanya bulat = baik, oleh karena itu, jika kita menetapkan turunan pada suatu titik seolah-olah kita ingin membuat busur di sana, kita akan mendapatkan kurva indah yang halus.

Akhir dari penyimpangan.

Tahap kedua dari pencarian turunan:

2. Melalui tiga titik kami vec1, vec2, vec3 kami membangun sebuah pesawat, di pesawat ini kami mencari lingkaran yang melewati ketiga titik. Derivatif yang diinginkan akan diarahkan sepanjang garis singgung ke lingkaran pada titik vec2, dan modulus vektor turunan harus sama dengan produk jari-jari lingkaran dan sudut sektor, yang membentuk dua titik permukaan poligon (mirip dengan analogi datar kami yang sederhana dari penyimpangan lirik).

$$

$$g '= R \ cdot \ phi$$

Segalanya tampak sederhana, di sini adalah kode fungsi, misalnya (NumPy digunakan lagi):


Nah, secara umum, semuanya entah bagaimana berhasil. Untuk demonstrasi, saya mengambil kubus 5x5x5 dan mengubah posisi poin dengan pengacak: