Mengapa kita membutuhkan rentang dari C ++ 20 dalam penghancur sederhana?

Baru-baru ini, rentang yang harus dimasukkan dalam standar C ++ 20 telah dibahas cukup banyak, termasuk pada Habré ( contoh di mana ada banyak contoh ). Ada cukup banyak kritik tentang interval, kata mereka

• mereka terlalu abstrak dan hanya diperlukan untuk kode yang sangat abstrak
• keterbacaan kode dengan mereka hanya memburuk
• interval memperlambat kode

Mari kita lihat sepenuhnya buruh-tani tugas praktis, untuk memahami apakah kritik ini valid dan apakah benar bahwa Eric Nibler digigit oleh Bartosz Milewski dan menulis range-v3 hanya dengan bulan purnama .

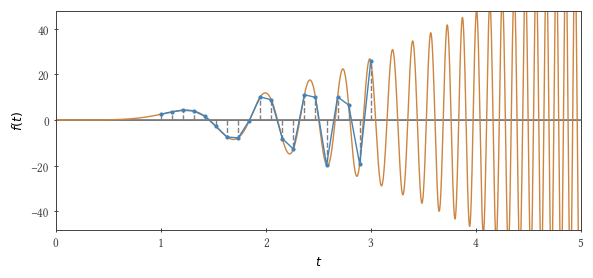
Kami akan mengintegrasikan fungsi berikut menggunakan metode trapesium:$$ $ inline $ f (t) = 3 t ^ 2 \ sin t ^ 3 $ inline $ mulai dari nol hingga$$ $ inline $ \ tau $ inline $ . Jika$$ $ inline $ \ tau ^ 3 / \ pi $ inline $ sama dengan angka ganjil, maka integralnya adalah 2.

Jadi, masalahnya: kita menulis prototipe fungsi yang menghitung integral dengan metode trapesium . Sekilas, tampaknya abstraksi tidak diperlukan di sini, tetapi kecepatan itu penting. Sebenarnya, ini tidak sepenuhnya benar. Untuk pekerjaan, saya sering harus menulis "penghancur angka", pengguna utamanya adalah saya sendiri. Jadi saya juga harus mendukung dan menangani bug mereka (sayangnya kolega saya - tidak selalu hanya saya). Dan itu juga terjadi bahwa beberapa kode tidak digunakan, katakanlah, setahun, dan kemudian ... Secara umum, dokumentasi dan tes juga perlu ditulis.

Argumen apa yang harus dimiliki fungsi integrator? Fungsi dan kisi yang terintegrasi (set point$$ $ sebaris $ t_1, t_2, t_3 ... $ sebaris $ digunakan untuk menghitung integral). Dan jika semuanya jelas dengan fungsi terintegrasi ( std::function akan ada di sini), lalu dalam bentuk apa seharusnya grid ditransmisikan? Ayo lihat.

Opsi

Untuk mulai dengan - untuk memiliki sesuatu untuk membandingkan kinerja - kita akan menulis sederhana for loop dengan langkah waktu yang konstan:

 // trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; } 

Saat menggunakan siklus ini, Anda bisa meneruskan argumen ke fungsi awal dan akhir interval integrasi, serta jumlah titik untuk integrasi ini sendiri. Stop - metode trapesium juga terjadi dengan langkah variabel, dan fungsi integrable kami hanya meminta untuk menggunakan langkah variabel! Jadi, mari kita punya satu parameter lagi ($$ $ inline $ b $ inline $ ) untuk mengontrol "nonlinier" dan biarkan langkah-langkah kami, misalnya, sebagai berikut:$$ $ inline $ \ Delta t (t) = \ Delta t_0 + bt $ inline $ . Pendekatan ini (memperkenalkan satu parameter numerik tambahan) mungkin digunakan di sejuta tempat, meskipun, tampaknya, cacatnya harus jelas bagi semua orang. Dan apakah kita memiliki fungsi yang berbeda? Dan jika kita membutuhkan langkah kecil di suatu tempat di tengah interval numerik kita? Tetapi bagaimana jika fungsi yang dapat diintegrasikan memiliki beberapa fitur? Secara umum, kita harus dapat menyampaikan grid apa pun . (Namun demikian, dalam contoh, hingga akhir, kami akan "lupa" tentang metode trapesium yang sebenarnya dan untuk kesederhanaan kami akan mempertimbangkan versinya dengan langkah konstan, dengan mengingat bahwa grid dapat berubah-ubah).

Karena kisi dapat berupa apa saja, mari berikan nilainya$$ $ inline $ t_1, t_2, ... $ inline $ terbungkus std::vector .

 // trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } 

Ada lebih dari cukup komunitas dalam pendekatan ini, tetapi bagaimana dengan kinerja? Dengan konsumsi memori? Jika sebelumnya semuanya disimpulkan pada prosesor, sekarang kita harus terlebih dahulu mengisi area memori, dan kemudian membacanya. Dan komunikasi dengan memori adalah hal yang agak lambat. Dan memori masih belum karet ( dan silikon )

Mari kita lihat akar masalahnya. Apa yang dibutuhkan seseorang untuk bahagia? Lebih tepatnya, apa yang dibutuhkan siklus kami (berbasis rentang untuk loop)? Kontainer apa pun dengan iterator begin() dan end() , dan ++ , * dan != Operator untuk iterator. Jadi kita akan menulis.

 //   ,    ,      template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... //      class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... //      lazy_container t_nodes; double res = integrate(t_nodes); 

Kami sedang menghitung nilai baru di sini.$$ $ inline $ t_i $ inline $ sesuai permintaan, seperti yang kami lakukan secara sederhana for loop. Tidak ada akses memori, dan diharapkan kompiler modern akan menyederhanakan kode dengan sangat efisien. Pada saat yang sama, kode fungsi integrasi tidak banyak berubah, dan masih dapat mencerna std::vector .

Di mana fleksibilitasnya? Bahkan, kita sekarang dapat menulis fungsi apa saja di operator ++ . Artinya, pendekatan ini memungkinkan, pada kenyataannya, untuk mentransfer fungsi alih-alih parameter numerik tunggal. Kotak yang dihasilkan dengan cepat dapat berupa apa saja, dan kami juga (mungkin) tidak kehilangan kinerja. Namun, untuk menulis lazy_container baru setiap saat hanya untuk entah bagaimana mendistorsi grid dengan cara baru tidak terasa seperti itu sama sekali (ini adalah 27 baris yang sama!). Tentu saja, Anda dapat membuat fungsi yang bertanggung jawab untuk menghasilkan grid sebagai parameter dari fungsi integrasi kami, dan lazy_container juga, yaitu, permisi, enkapsulasi.

Anda bertanya - lalu ada sesuatu yang salah lagi? Ya! Pertama, akan diperlukan untuk secara terpisah mengirimkan jumlah poin untuk integrasi, yang dapat menyebabkan kesalahan. Kedua, sepeda non-standar yang dibuat harus didukung dan mungkin dikembangkan oleh seseorang. Sebagai contoh, dapatkah Anda segera membayangkan bagaimana, dengan pendekatan ini, untuk menyusun kombinator untuk fungsi-fungsi di operator ++ ?

C ++ selama lebih dari 30 tahun. Banyak di usia ini sudah memiliki anak, dan C ++ bahkan tidak memiliki wadah / iterator malas standar. Mimpi buruk! Tetapi semuanya (dalam arti iterator, bukan anak-anak) akan berubah pada awal tahun depan - standar (mungkin sebagian) akan mencakup perpustakaan range-v3 , yang telah dikembangkan oleh Eric Nibler selama beberapa tahun. Kami akan menggunakan karya buahnya. Kode mengatakan semuanya untuk dirinya sendiri:

 #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes); 

Fungsi pengintegrasian tetap sama. Artinya, hanya 3 baris untuk menyelesaikan masalah kita! Di sini iota_view(0, n) menghasilkan interval malas (rentang, objek yang merangkum awal dan akhir yang digeneralisasi; rentang lazy adalah tampilan), yang, ketika mengulangi pada setiap langkah, menghitung angka berikutnya dalam rentang [0, n). Lucu bahwa nama ι (huruf Yunani iota) merujuk 50 tahun yang lalu ke bahasa APL. Tongkat | memungkinkan Anda untuk menulis pipa pengubah interval, dan transform , pada kenyataannya, adalah pengubah sedemikian rupa sehingga, menggunakan fungsi lambda sederhana, mengubah urutan bilangan bulat menjadi satu rangkaian$$ $ inline $ t_1, t_2, ... $ inline $ . Semuanya sederhana, seperti pada dongeng Haskell.

Tapi bagaimana cara membuat langkah variabel? Semuanya sesederhana:

 #include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes); 

Pembaca yang penuh perhatian mencatat bahwa dalam contoh kami, langkah variabel memungkinkan kami untuk mengurangi jumlah titik kisi dengan faktor tiga, sementara di samping itu, ada biaya nyata untuk komputasi$$ $ inline $ t_i $ inline $ . Tetapi jika kita mengambil yang lain$$ $ inline $ f (t) $ inline $ , jumlah poin bisa berubah lebih banyak ... (tapi di sini penulis sudah menjadi malas).

Jadi timing

Kami memiliki opsi berikut:

• v1 - loop sederhana
• v2 -$$ $ inline $ t_i $ inline $ berbaring di std::vector
• v3 - lazy_container darurat dengan iterator darurat
• v4 - interval dari C ++ 20 (rentang)
• v5 - berkisar lagi, tetapi hanya di sini metode trapesium ditulis menggunakan pitch variabel

Inilah hasilnya (dalam detik) untuk$$ $ inline $ \ tau = (10 \, 000 \, 001 \ kali \ pi) ^ {1/3} $ inline $ , untuk g ++ 8.3.0 dan clang ++ 8.0.0 pada Intel® Xeon® CPU® X5550 (jumlah langkah sekitar$$ $ inline $ 1.5 \ kali 10 ^ 8 $ inline $ , kecuali untuk v5, di mana langkah-langkahnya tiga kali lebih sedikit (hasil perhitungan oleh semua metode berbeda dari keduanya dengan tidak lebih dari 0,07):

Secara umum, lalat pergi melintasi lapangan, lalat menemukan koin!

Ringkasan

Bahkan dalam tugas yang sangat sederhana, rentang ternyata sangat berguna: alih-alih kode dengan iterator buatan sendiri pada 20+ baris, kami menulis 3 baris, sementara tidak memiliki masalah dengan keterbacaan kode atau kinerjanya.

Tentu saja, jika kami membutuhkan (untuk) kinerja terbaik dalam tes ini, kami harus mendapatkan hasil maksimal dari prosesor dan dari memori dengan menulis kode paralel (atau menulis versi di bawah OpenCL) ... Juga, saya tidak tahu apa yang akan terjadi jika saya menulis rantai pengubah yang sangat panjang. Apakah mudah untuk men-debug dan membaca pesan kompiler saat menggunakan rentang dalam proyek yang kompleks. Akan mengumpulkan waktu meningkat. Saya harap seseorang pernah menulis tentang artikel ini.

Ketika saya menulis tes ini, saya sendiri tidak tahu apa yang akan terjadi. Sekarang saya tahu - rentang pasti layak untuk diuji dalam proyek nyata, dalam kondisi di mana Anda bermaksud menggunakannya.

Saya pergi ke pasar untuk membeli samovar.

Tautan yang bermanfaat

range-v3 rumah

Dokumentasi dan Studi Kasus v3

kode dari artikel ini di github

daftar di haskell, untuk perbandingan

Ucapan Terima Kasih

Terima kasih fadey untuk membantu menulis ini semua!

PS

Saya harap seseorang mengomentari keanehan tersebut: i) Jika Anda mengambil interval integrasi 10 kali lebih kecil, maka pada Xeon saya contoh v2 adalah 10% lebih cepat dari v1, dan v4 tiga kali lebih cepat dari v1. ii) Kompiler Intel (icc 2019) kadang-kadang dalam contoh ini membuat kode yang dua kali lebih cepat dari kompilasi g ++. Apakah vektorisasi harus disalahkan? Bisakah g ++ dipaksa melakukan hal yang sama?