Pengantar Ketergantungan Fungsional

Pada artikel ini kita akan berbicara tentang dependensi fungsional dalam database - apa itu, di mana ia diterapkan dan algoritma apa yang ada untuk pencarian mereka.

Kami akan mempertimbangkan dependensi fungsional dalam konteks database relasional. Berbicara dengan sangat kasar, dalam database seperti itu informasi disimpan dalam bentuk tabel. Selanjutnya, kita menggunakan konsep perkiraan, yang dalam teori relasional yang ketat tidak dapat dipertukarkan: kita akan menyebut tabel itu sendiri relasi, kolom - atribut (himpunannya adalah diagram hubungan), dan satu set nilai baris pada subset atribut - tupel.



Misalnya, dalam tabel di atas, (Benson, M, M organ ) adalah tupel atribut (Pasien, Jenis Kelamin, Dokter) .
Secara lebih formal, ini ditulis sebagai berikut: $$$t_ {1}$[ Pasien, Paul, Dokter ] = (Benson, M, M organ) .
Sekarang kita dapat memperkenalkan konsep ketergantungan fungsional (FZ):

Definisi 1. Relasi R memenuhi hukum federal X → Y (di mana X, Y ⊆ R) jika dan hanya jika untuk setiap tupel $$$t_ {1}$, $$$t_ {2}$∈ R berlaku: jika $$$t_ {1}$[X] = $$$t_ {2}$[X] lalu $$$t_ {1}$[Y] = $$$t_ {2}$[Y]. Dalam hal ini, dikatakan bahwa X (determinan, atau sekumpulan atribut yang menentukan) secara fungsional mendefinisikan Y (sekumpulan dependen).

Dengan kata lain, kehadiran Undang-Undang Federal X → Y berarti bahwa jika kita memiliki dua tupel dalam R dan keduanya bertepatan dalam atribut X , maka keduanya juga akan bertepatan dalam atribut Y.
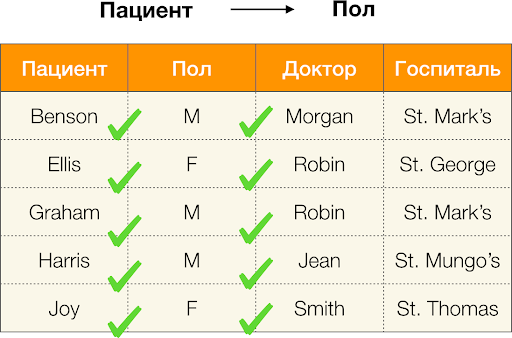
Dan sekarang dalam rangka. Pertimbangkan atribut Pasien dan Jender yang ingin kita cari tahu apakah ada ketergantungan di antara mereka atau tidak. Untuk banyak atribut, dependensi berikut mungkin ada:

1. Pasien → Jenis Kelamin
2. Gender → Pasien

Menurut definisi di atas, untuk mempertahankan ketergantungan pertama, hanya satu nilai kolom Gender yang harus sesuai dengan setiap nilai unik kolom Pasien . Dan untuk tabel sampel, ini benar. Namun, ini tidak bekerja dalam arah yang berlawanan, yaitu, ketergantungan kedua tidak terpenuhi, dan atribut Paul bukan merupakan penentu bagi Pasien . Demikian pula, jika Anda mengambil ketergantungan Dokter → Pasien , Anda dapat melihat bahwa itu dilanggar, karena nilai Robin untuk atribut ini memiliki beberapa nilai yang berbeda - Ellis dan Graham .

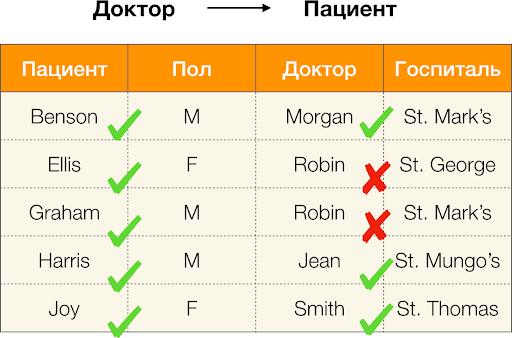
Dengan demikian, dependensi fungsional memungkinkan untuk menentukan hubungan yang ada antara set atribut tabel. Untuk selanjutnya, kami akan mempertimbangkan hubungan yang paling menarik, atau lebih tepatnya X → Y sedemikian rupa sehingga mereka adalah:

• nontrivial, yaitu, sisi kanan ketergantungan bukanlah subset dari kiri (Y ̸⊆ X) ;
• minimal, yaitu, tidak ada ketergantungan Z → Y sedemikian sehingga Z ⊂ X.

Ketergantungan yang dianggap sampai saat ini sangat ketat, yaitu, mereka tidak termasuk pelanggaran di atas meja, tetapi selain itu ada juga yang memungkinkan beberapa ketidakkonsistenan antara nilai-nilai tupel. Ketergantungan tersebut ditempatkan di kelas yang terpisah, yang disebut perkiraan, dan diizinkan untuk dilanggar pada sejumlah tupel. Jumlah ini diatur oleh indikator kesalahan emax maksimum. Misalnya proporsi kesalahan $$$e_ {maks}$= 0,01 dapat berarti bahwa ketergantungan dapat dilanggar oleh 1% dari tupel yang tersedia pada set atribut yang dianggap. Artinya, untuk 1000 catatan, maksimal 10 tupel dapat melanggar Hukum Federal. Kami akan mempertimbangkan metrik yang sedikit berbeda berdasarkan nilai yang berbeda berpasangan dari tupel yang dibandingkan. Untuk ketergantungan X → Y pada relasi r, dianggap sebagai berikut:

$$

$$e (X \ rightarrow Y, r) = \ frac {| \ {(t_1, t_2) \ dalam r ^ 2 \ | \ t_1 [X] = t_2 [X] \ wedge t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | r |}$$

Kami menghitung kesalahan untuk Dokter → Pasien dari contoh di atas. Kami memiliki dua tupel, yang nilainya berbeda pada atribut Pasien , tetapi bertepatan dengan Dokter : $$$t_ {1}$[ Dokter, Pasien ] = ( Robin, Ellis ) dan $$$t_ {2}$[ Dokter, Pasien ] = ( Robin, Graham ). Mengikuti definisi kesalahan, kita harus memperhitungkan semua pasangan yang saling bertentangan, yang berarti akan ada dua pasangan: ( $$$t_ {1}$, $$$t_ {2}$) dan inversinya ( $$$t_ {2}$, $$$t_ {1}$) Pengganti dalam rumus dan dapatkan:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0,1$$

Sekarang mari kita coba menjawab pertanyaan: "Mengapa semuanya?". Faktanya, Hukum Federal berbeda. Tipe pertama adalah dependensi yang ditentukan oleh administrator pada tahap desain database. Biasanya mereka sedikit, mereka ketat, dan aplikasi utamanya adalah normalisasi data dan desain skema hubungan.

Tipe kedua adalah dependensi yang mewakili data "tersembunyi" dan hubungan yang sebelumnya tidak diketahui antara atribut. Artinya, dependensi tersebut tidak dipikirkan pada saat desain dan sudah ditemukan untuk set data yang ada, sehingga, berdasarkan pada set hukum federal yang diidentifikasi, untuk menarik kesimpulan tentang informasi yang disimpan. Dengan ketergantungan itulah kami bekerja. Mereka terlibat dalam seluruh area penambangan data dengan berbagai teknik pencarian dan algoritma yang dibangun atas dasar mereka. Mari kita memahami bagaimana dependensi fungsional yang ditemukan (tepat atau perkiraan) dalam data apa pun dapat berguna.



Saat ini, pembersihan data adalah salah satu bidang utama penggunaan ketergantungan. Ini melibatkan pengembangan proses untuk mengidentifikasi "data kotor" dengan koreksi selanjutnya. Perwakilan terang dari "data kotor" adalah duplikat, kesalahan atau kesalahan ketik data, nilai yang hilang, data yang ketinggalan zaman, ruang ekstra dan sejenisnya.

Contoh data kesalahan:



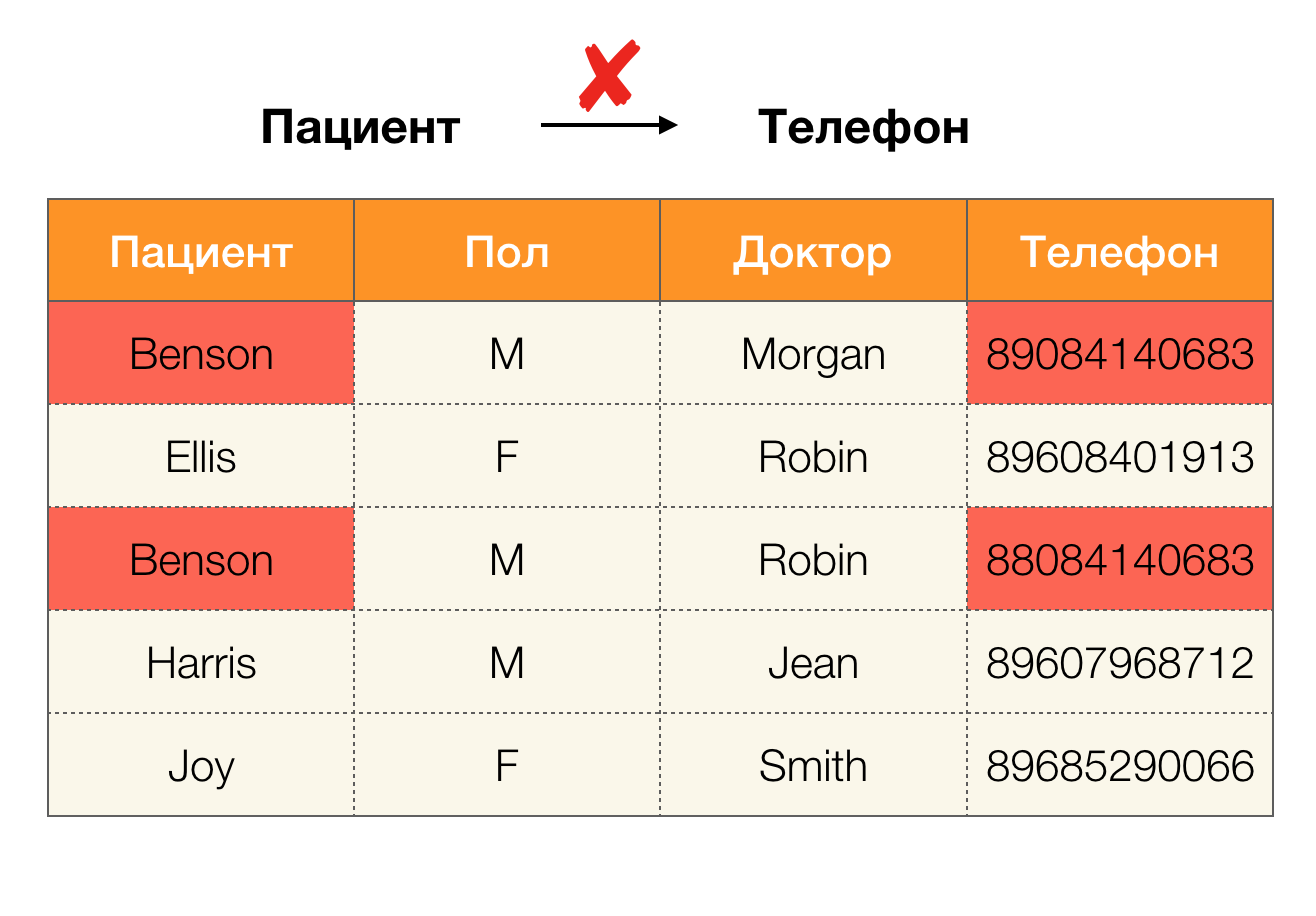
Contoh duplikat dalam data:



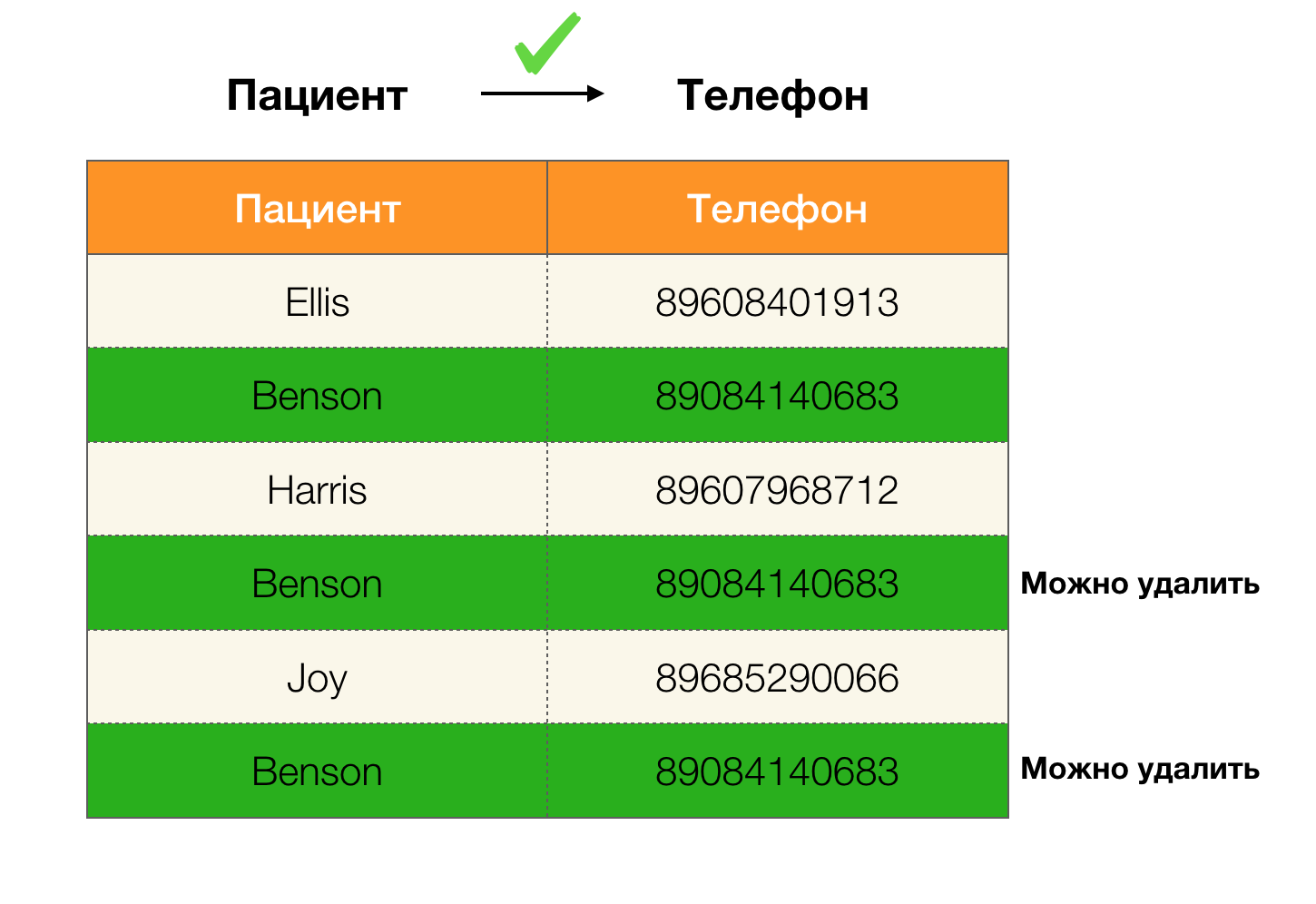
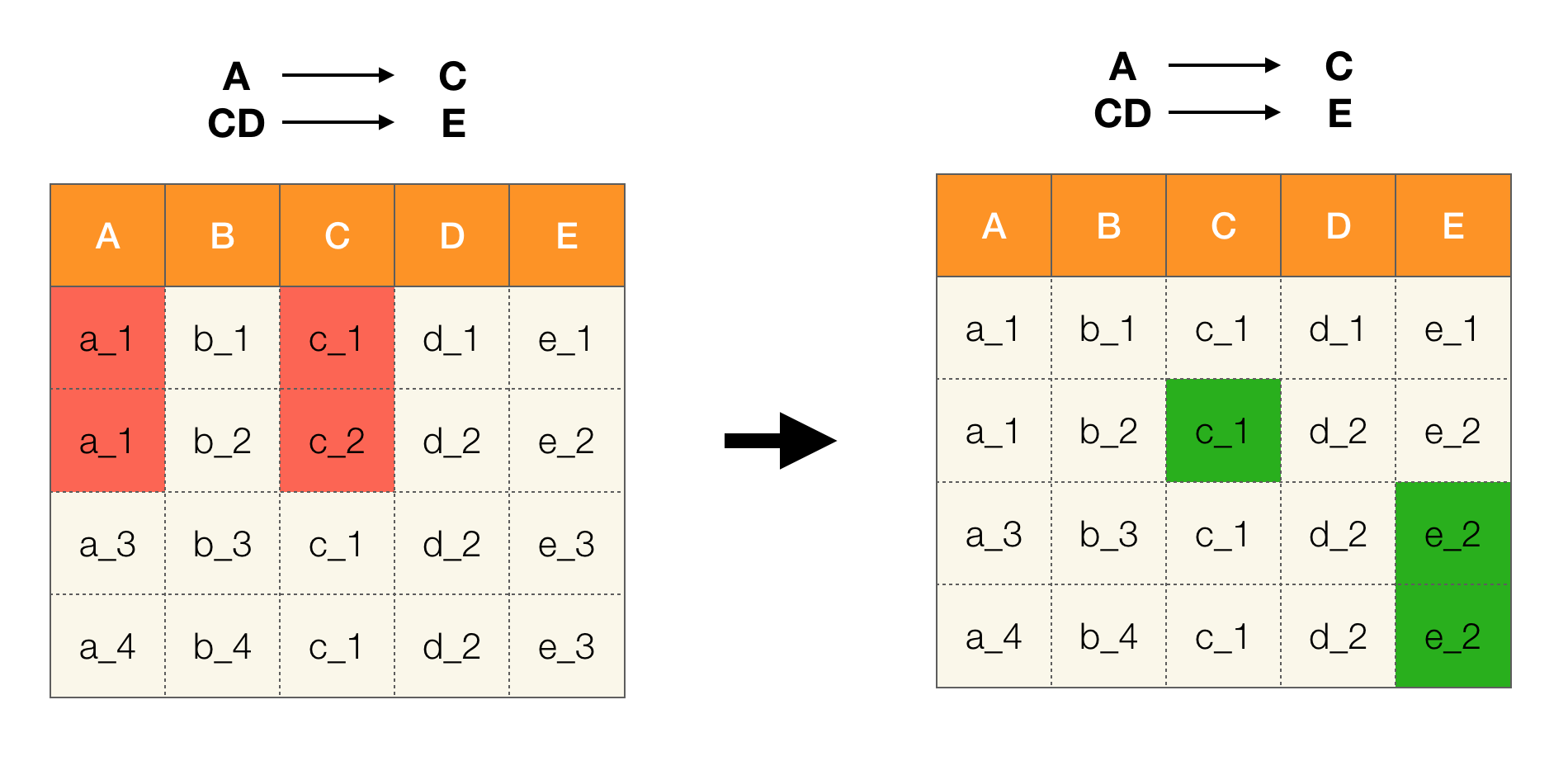
Misalnya, kami memiliki tabel dan seperangkat Hukum Federal yang harus dieksekusi. Pembersihan data dalam hal ini melibatkan pengubahan data sehingga Undang-Undang Federal benar. Pada saat yang sama, jumlah modifikasi harus minimal (untuk prosedur ini, ada algoritma yang tidak akan kami fokuskan dalam artikel ini). Berikut ini adalah contoh konversi data tersebut. Di sebelah kiri adalah hubungan awal, di mana, jelas, hukum federal yang diperlukan tidak dipenuhi (contoh pelanggaran salah satu hukum federal disorot dengan warna merah). Di sebelah kanan adalah hubungan yang diperbarui di mana sel hijau menunjukkan nilai yang berubah. Setelah prosedur seperti itu, ketergantungan yang diperlukan mulai terasa.



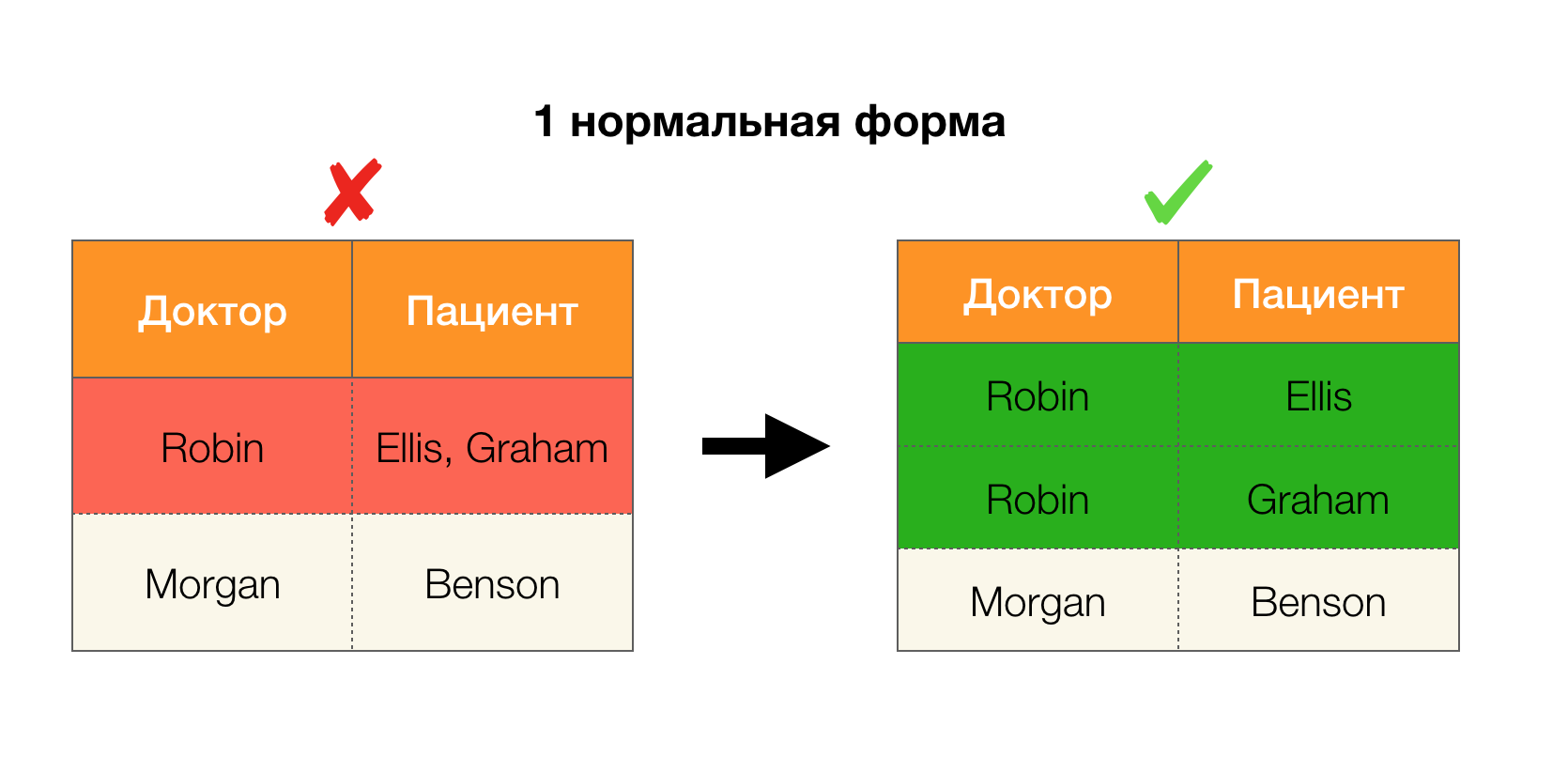
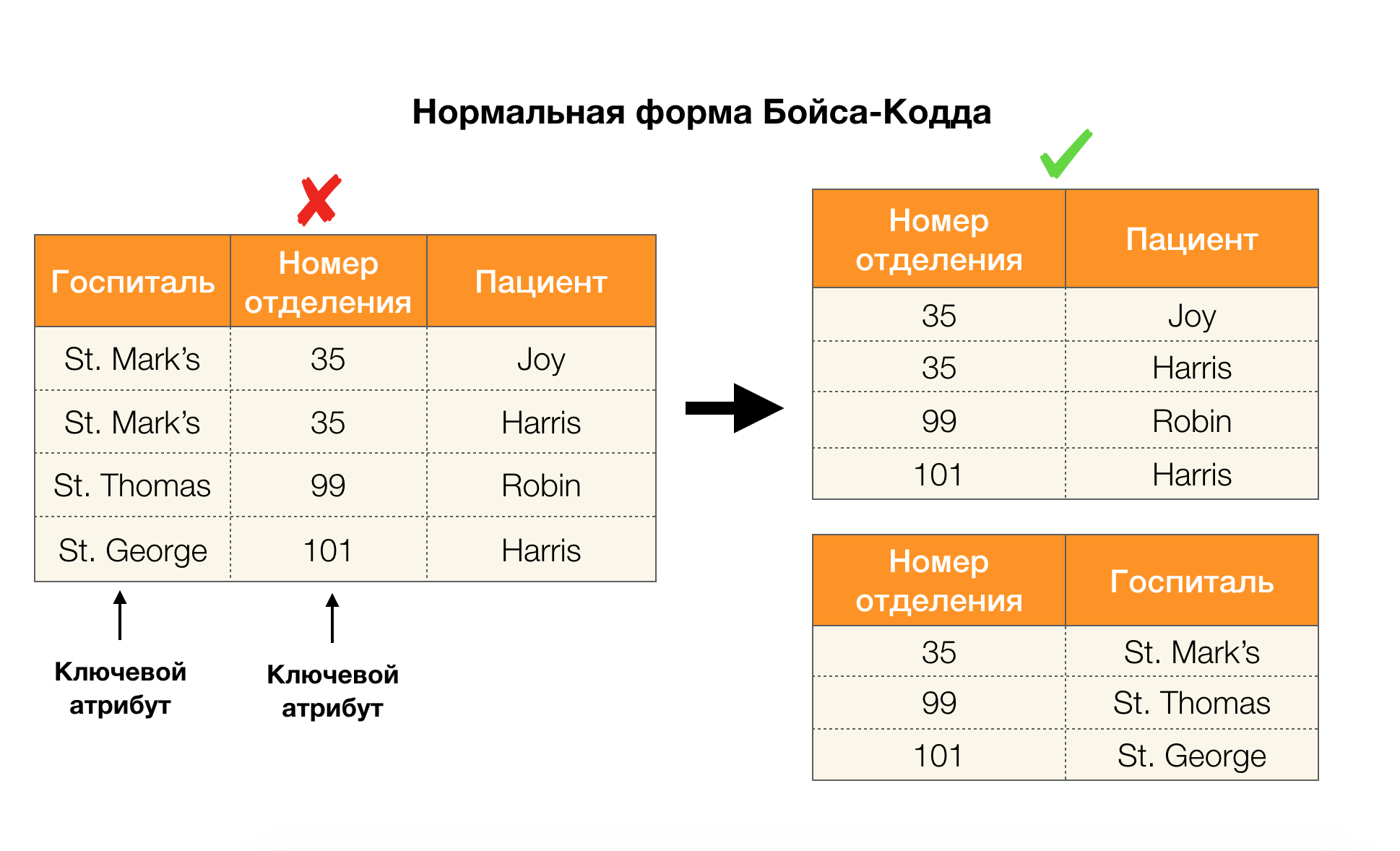
Aplikasi populer lainnya adalah desain basis data. Di sini perlu diingat tentang bentuk-bentuk normal dan normalisasi. Normalisasi adalah proses menyatukan hubungan dengan serangkaian persyaratan tertentu, yang masing-masing ditentukan dengan caranya sendiri oleh bentuk normal. Kami tidak akan menuliskan persyaratan berbagai bentuk normal (ini dilakukan dalam buku apa pun tentang kursus DB untuk pemula), tetapi kami hanya mencatat bahwa masing-masing dari mereka dengan caranya sendiri menggunakan konsep dependensi fungsional. Memang, Hukum Federal secara inheren kendala integritas yang diperhitungkan ketika merancang database (dalam konteks tugas ini, Hukum Federal kadang-kadang disebut kunci super).

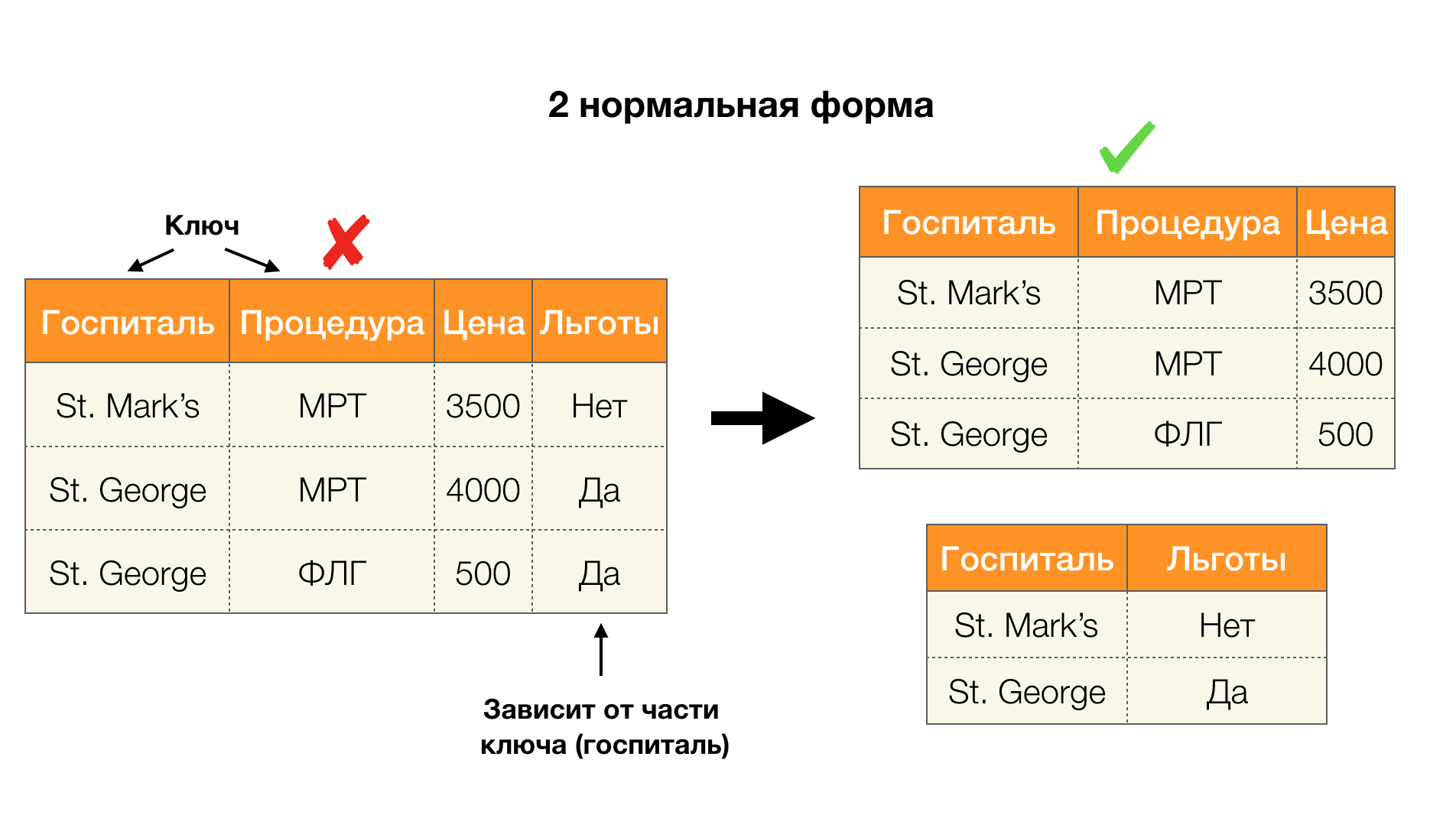
Pertimbangkan aplikasi mereka untuk empat bentuk normal pada gambar di bawah ini. Ingat bahwa bentuk Boyce-Codd normal lebih ketat dari bentuk ketiga, tetapi kurang ketat dari yang keempat. Kami belum mempertimbangkan yang terakhir, karena formulasinya membutuhkan pemahaman tentang ketergantungan multi-nilai, yang tidak menarik bagi kami dalam artikel ini.






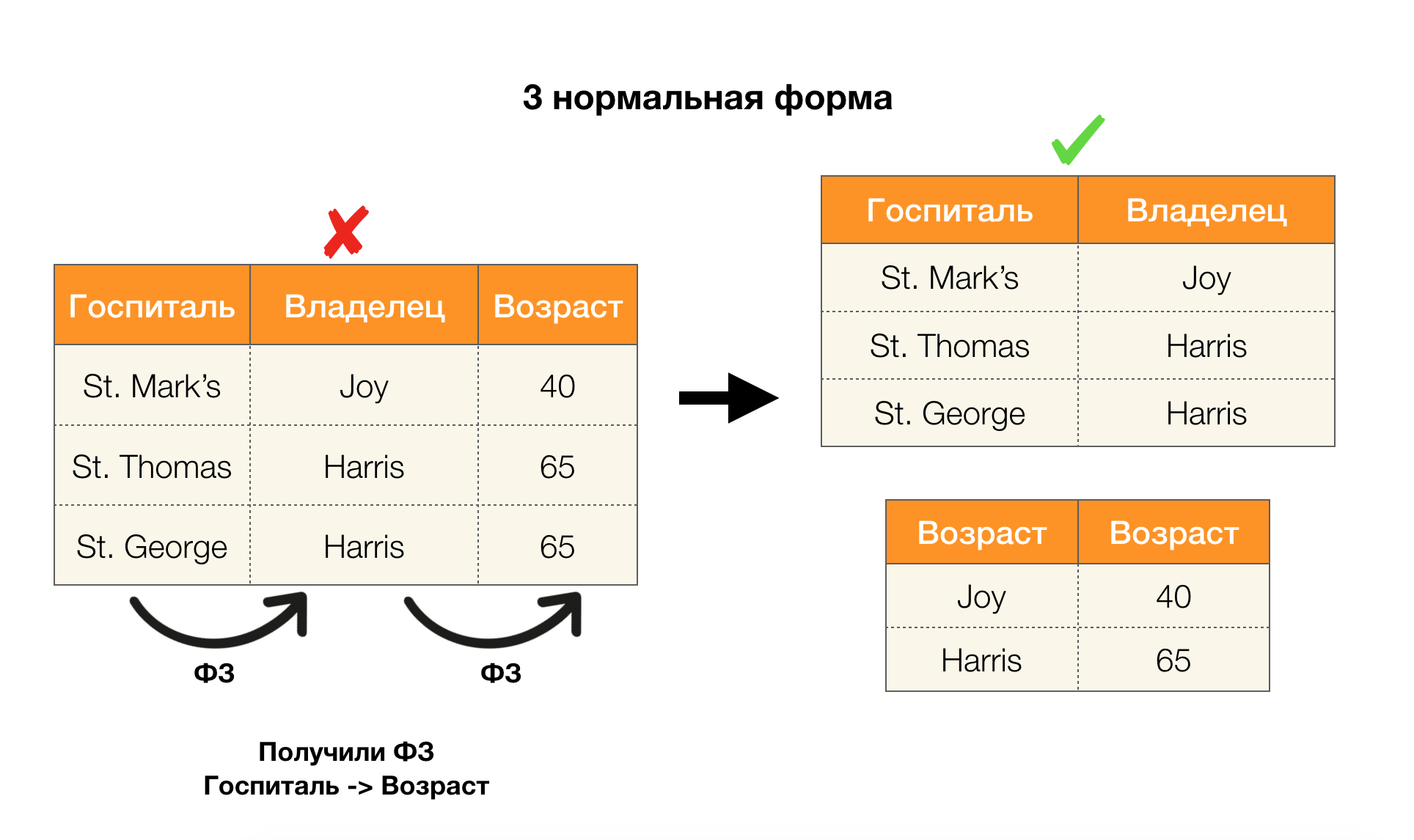
Daerah lain di mana dependensi telah menemukan aplikasi mereka adalah pengurangan dimensi ruang fitur dalam tugas-tugas seperti pembangunan classifier Bayesian yang naif, identifikasi fitur signifikan, dan reparametrization dari model regresi. Dalam artikel asli, masalah ini disebut definisi fitur yang berlebihan (redundansi fitur) dan relevan (relevansi fitur) [5, 6], dan diselesaikan dengan penggunaan aktif konsep-konsep basis data. Dengan munculnya karya-karya seperti itu, kita dapat mengatakan bahwa hari ini ada permintaan untuk solusi yang memungkinkan menggabungkan database, analisis dan implementasi dari masalah optimasi di atas menjadi satu alat [7, 8, 9].

Ada banyak algoritma (baik yang modern maupun yang tidak terlalu) untuk mencari Hukum Federal dalam kumpulan data. Algoritma tersebut dapat dibagi menjadi tiga kelompok:

• Algoritma menggunakan traversal of algebraic lattices (Lattice traversal algorithmms)
• Algoritma berdasarkan pencarian untuk nilai-nilai yang konsisten (Algoritma yang berbeda dan setuju)
• Algoritma Perbandingan Berpasangan (Algoritma induksi ketergantungan)
  

Deskripsi singkat dari masing-masing jenis algoritma disajikan dalam tabel di bawah ini:


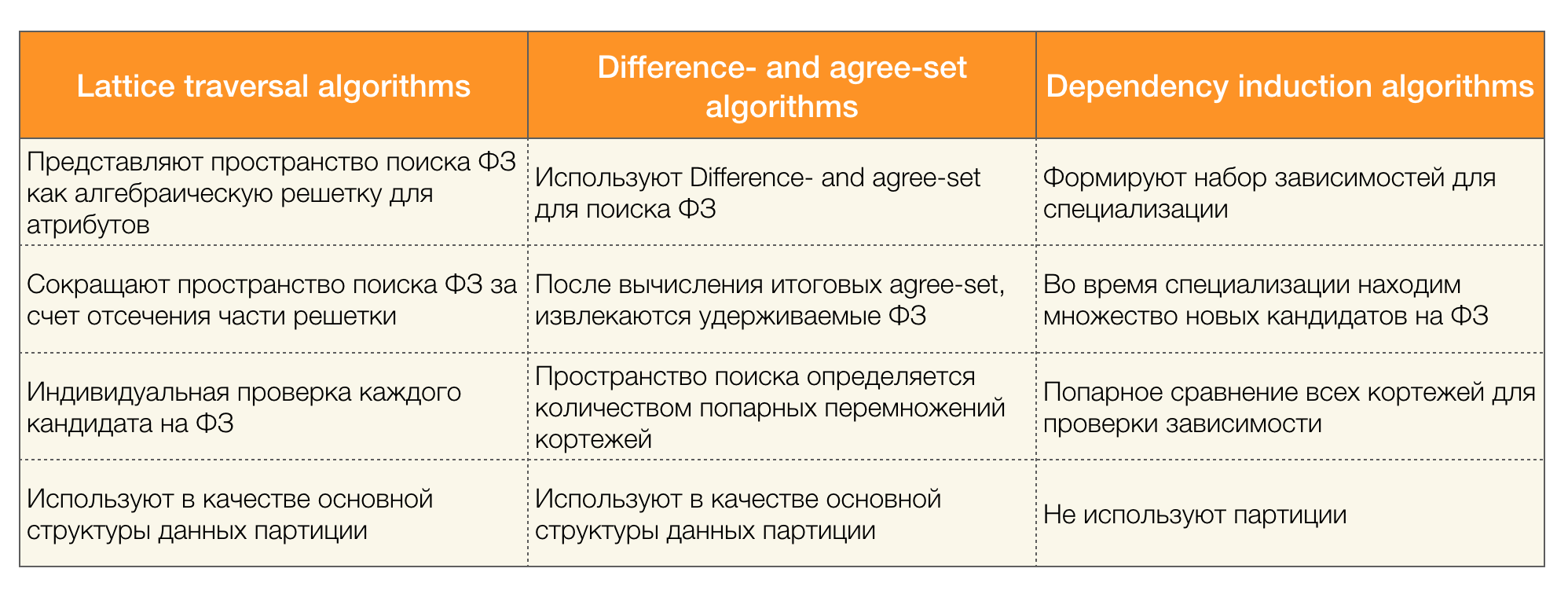
Rincian lebih lanjut tentang klasifikasi ini dapat dibaca [4]. Di bawah ini adalah contoh algoritma untuk setiap jenis:





Saat ini, muncul algoritma baru yang menggabungkan beberapa pendekatan untuk mencari dependensi fungsional sekaligus. Contoh dari algoritma tersebut adalah Pyro [2] dan HyFD [3]. Analisis pekerjaan mereka diharapkan dalam artikel-artikel berikut dari seri ini. Dalam artikel ini, kami hanya akan menganalisis konsep dasar dan lemma yang diperlukan untuk memahami teknik-teknik untuk mendeteksi dependensi.

Mari kita mulai dengan yang sederhana - berbeda dan setuju-set, digunakan dalam jenis kedua algoritma. Set perbedaan adalah seperangkat tupel yang tidak cocok dengan nilai, dan set setuju, sebaliknya, adalah tupel yang cocok dengan nilai. Perlu dicatat bahwa dalam kasus ini kami hanya mempertimbangkan sisi kiri ketergantungan.

Juga konsep penting yang dipenuhi di atas adalah kisi aljabar. Karena banyak algoritma modern beroperasi pada konsep ini, kita perlu memiliki gagasan tentang apa itu.

Untuk memperkenalkan konsep kisi, perlu untuk menetapkan set yang dipesan sebagian (atau set yang dipesan sebagian, untuk pos - poset pendek).

Definisi 2. Dikatakan bahwa himpunan S sebagian dipesan oleh relasi biner ⩽ jika untuk a, b, c ∈ S, properti berikut dipenuhi:

1. Refleksivitas, yaitu a ⩽ a
2. Antisimetri, yaitu, jika ⩽ b dan b ⩽ a, maka a = b
3. Transitivitas, yaitu, untuk ⩽ b dan b ⩽ c berarti a ⩽ c
   

Relasi semacam itu disebut relasi urutan parsial (tidak ketat), dan set itu sendiri disebut set yang dipesan sebagian. Notasi formal: ⟨S, ⩽⟩.

Sebagai contoh paling sederhana dari himpunan yang dipesan sebagian, kita dapat mengambil himpunan semua bilangan asli N dengan hubungan urutan ⩽ yang biasa. Sangat mudah untuk memverifikasi bahwa semua aksioma yang diperlukan terpenuhi.

Contoh yang lebih bermakna. Pertimbangkan himpunan semua himpunan bagian {1, 2, 3} yang dipesan oleh relasi inklusi ⊆. Memang, hubungan ini memenuhi semua kondisi urutan parsial, oleh karena itu, ⟨P ({1, 2, 3}), ⊆⟩ adalah himpunan yang dipesan sebagian. Gambar di bawah ini menunjukkan struktur himpunan ini: jika dari satu elemen Anda dapat berjalan di sepanjang panah ke elemen lain, maka mereka terkait dengan pesanan.



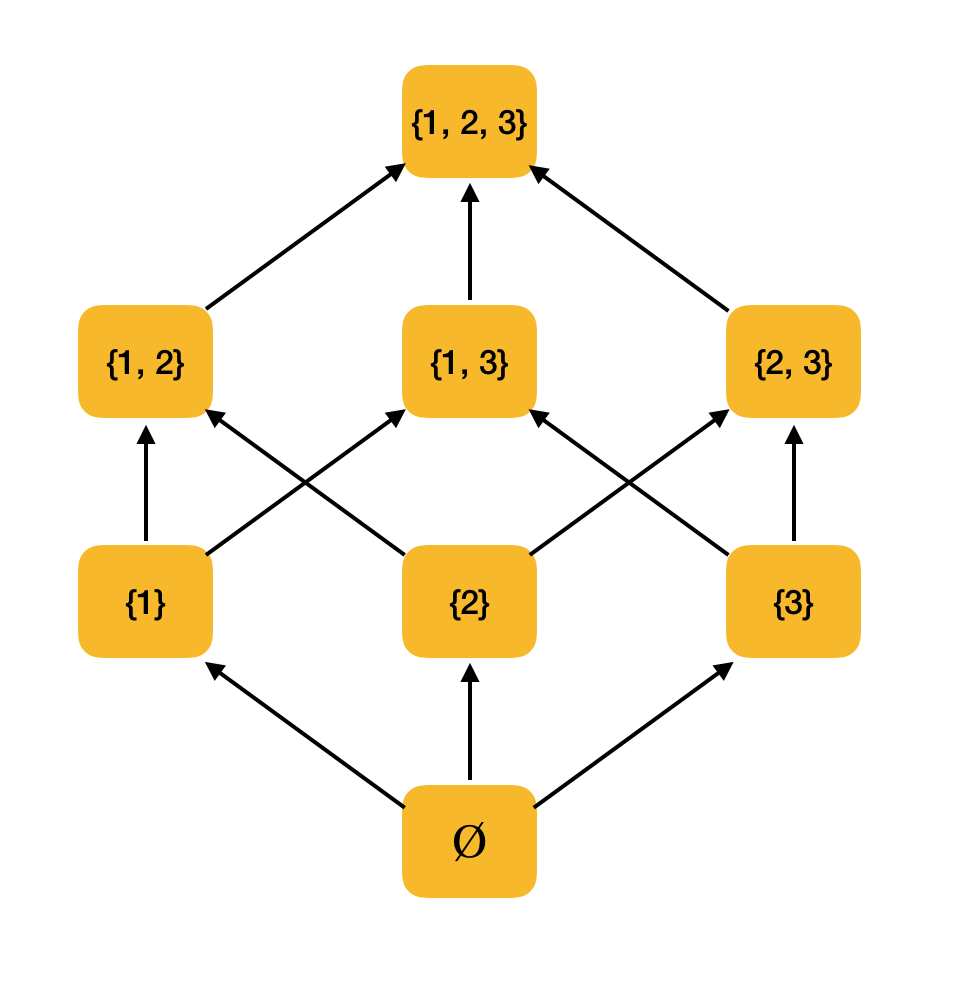
Kita akan membutuhkan dua definisi sederhana lagi dari bidang matematika - supremum dan infimum.

Definisi 3. Misalkan ⟨S, ⩽⟩ adalah himpunan yang diurutkan sebagian, A ⊆ S. Batas atas A adalah elemen u ∈ S sedemikian rupa sehingga ∀x ∈ A: x ⩽ u. Biarkan U menjadi himpunan semua batas atas A. Jika U memiliki elemen terkecil, maka itu disebut supremum dan dilambangkan dengan sup A.

Demikian pula, konsep batas bawah yang tepat diperkenalkan.

Definisi 4. Misalkan ⟨S, ⩽⟩ menjadi himpunan yang diurutkan sebagian, A ⊆ S. Batas bawah A adalah elemen l ∈ S sedemikian rupa sehingga ∀x ∈ A: l ⩽ x. Misalkan L adalah himpunan semua batas bawah A. Jika L memiliki elemen terbesar, maka itu disebut infimum dan dilambangkan dengan inf.

Pertimbangkan, sebagai contoh, set ⟨P yang dipesan sebagian ({1, 2, 3}) di atas, dan temukan supremum dan infimum di dalamnya:



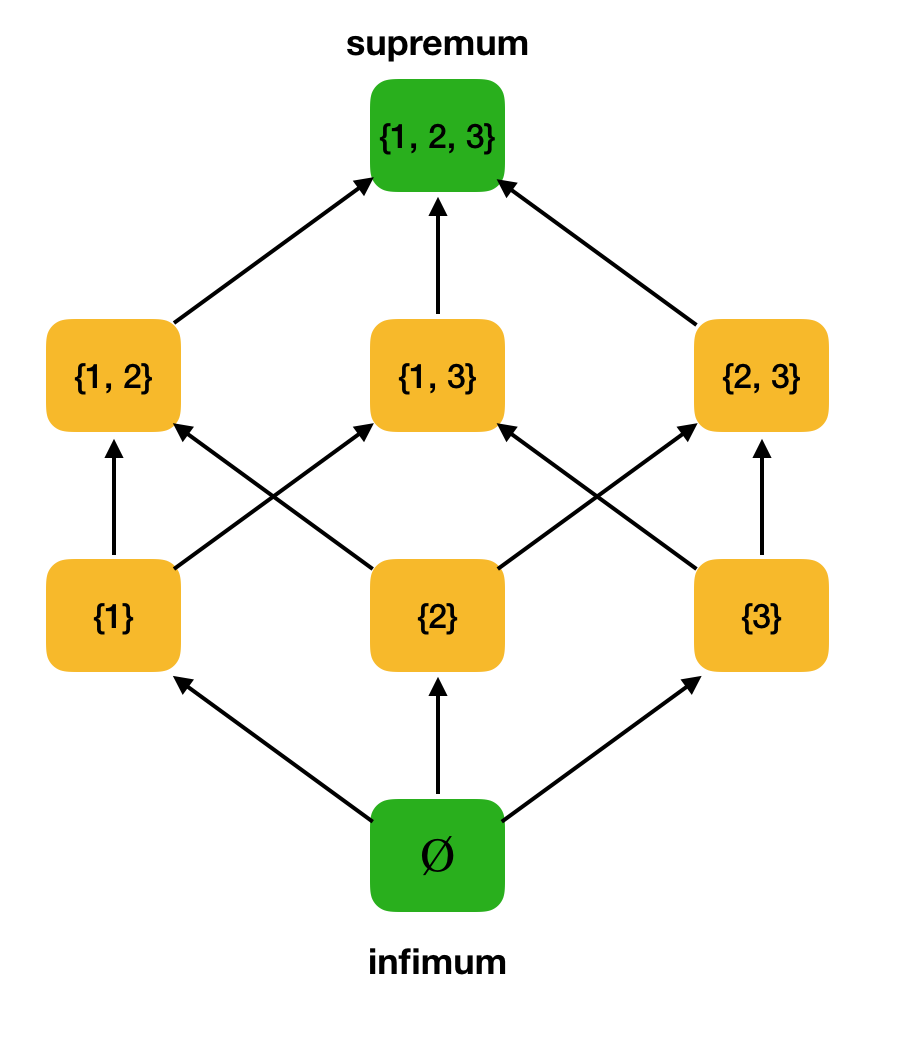
Sekarang kita dapat merumuskan definisi kisi aljabar.

Definisi 5. Misalkan ⟨P, ⩽⟩ adalah himpunan yang diurutkan sebagian sehingga setiap subset dua elemen memiliki batas atas dan bawah yang tepat. Kemudian P disebut kisi aljabar. Selain itu, sup {x, y} ditulis sebagai x ∨ y, dan inf {x, y} - sebagai x ∧ y.

Kami memverifikasi bahwa contoh kerja kami ⟨P ({1, 2, 3}), ⊆⟩ adalah sebuah kisi. Memang, untuk a, b ∈ P ({1, 2, 3}), a∨b = a∪b, dan a∧b = a∩b. Sebagai contoh, pertimbangkan set {1, 2} dan {1, 3} dan temukan infimum dan supremumnya. Jika kita melewatinya, kita mendapatkan set {1}, yang akan menjadi yang paling tinggi. Kami mendapatkan supremum melalui persatuan mereka - {1, 2, 3}.

Dalam algoritma deteksi FD, ruang pencarian sering direpresentasikan dalam bentuk kisi, di mana set satu elemen (baca level pertama dari kisi pencarian, di mana bagian kiri dependensi terdiri dari satu atribut) adalah masing-masing atribut dari hubungan asli.
Pada awalnya, ketergantungan bentuk ∅ → Atribut tunggal dipertimbangkan. Langkah ini memungkinkan Anda untuk menentukan atribut mana yang merupakan kunci utama (tidak ada penentu untuk atribut tersebut, dan oleh karena itu sisi kiri kosong). Lebih lanjut, algoritma tersebut bergerak ke atas kisi. Perlu dicatat bahwa kisi tidak dapat mem-bypass semua, yaitu, jika ukuran maksimum yang diinginkan dari bagian kiri ditransmisikan ke input, algoritma tidak akan melampaui level dengan ukuran ini.

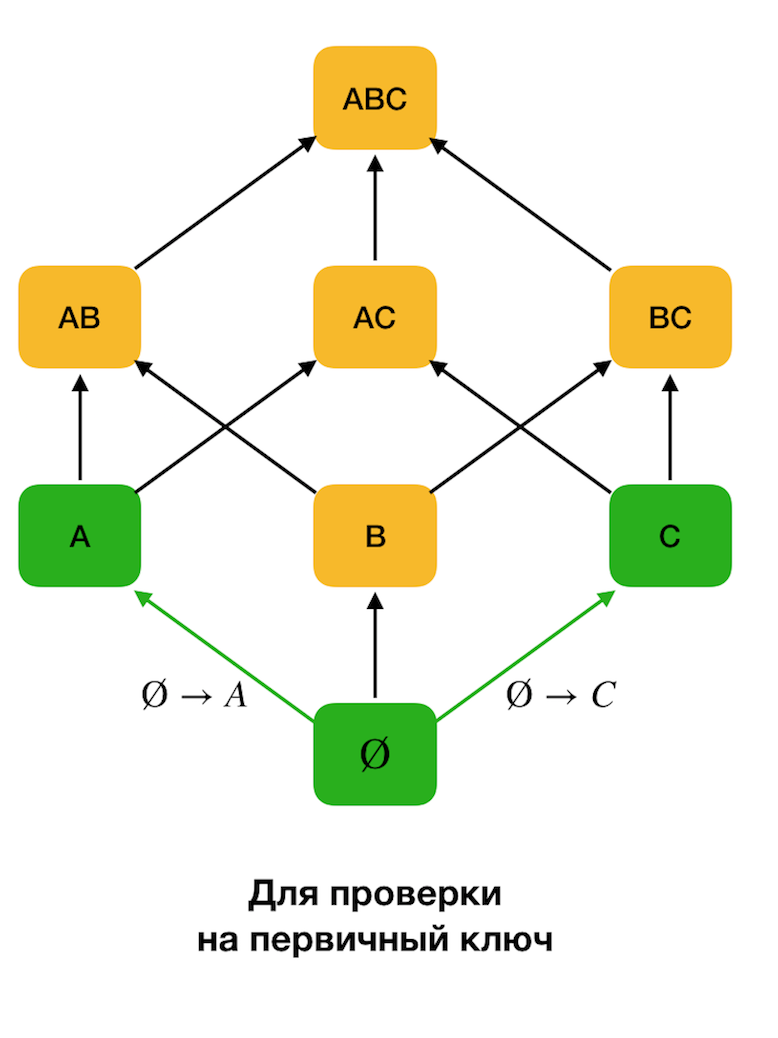
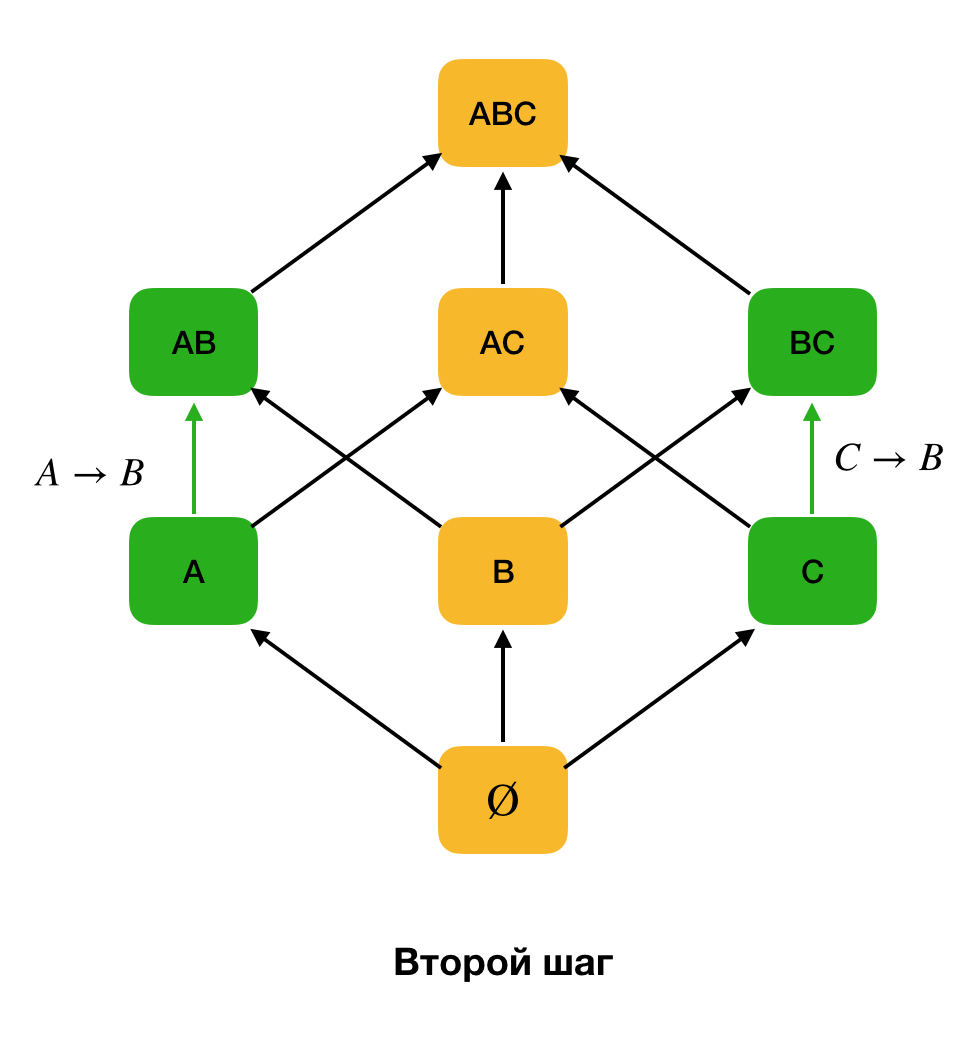
Gambar di bawah ini menunjukkan bagaimana Anda dapat menggunakan kisi aljabar dalam masalah pencarian untuk Hukum Federal. Di sini, setiap sisi ( X, XY ) mewakili ketergantungan X → Y. Sebagai contoh, kami melewati level pertama dan kami tahu bahwa ketergantungan A → B disimpan (kami akan menampilkan ini dengan koneksi hijau antara simpul A dan B ). Karena itu, ketika kita menaikkan kisi ke atas, kita tidak dapat memeriksa ketergantungan A, C → B , karena itu tidak lagi minimal. Demikian pula, kami tidak akan mengujinya jika ketergantungan C → B dipertahankan.




Selain itu, sebagai aturan, semua algoritma pencarian FZ modern menggunakan struktur data seperti partisi (partisi yang dilucuti [1] pada sumber aslinya). Definisi formal partisi adalah sebagai berikut:

Definisi 6. Misalkan X ⊆ R adalah himpunan atribut untuk relasi r. Cluster adalah sekumpulan indeks tupel dari r yang memiliki nilai X yang sama, yaitu, c (t) = {i | ti [X] = t [X]}. Partisi adalah seperangkat kelompok, tidak termasuk kelompok panjang unit:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ wedge | c (t) | > 1 \}$$

Dengan kata sederhana, partisi untuk atribut X adalah seperangkat daftar, di mana setiap daftar berisi nomor baris dengan nilai yang sama untuk X. Dalam literatur modern, struktur yang mewakili partisi disebut indeks daftar posisi (PLI). Cluster panjang unit dikecualikan untuk kompresi PLI karena mereka adalah cluster yang hanya berisi nomor rekaman dengan nilai unik yang akan selalu mudah diatur.

Pertimbangkan sebuah contoh. Mari kita kembali ke tabel yang sama dengan pasien dan membangun partisi untuk kolom Pasien dan Paul (kolom baru muncul di sebelah kiri, di mana nomor baris tabel ditandai):





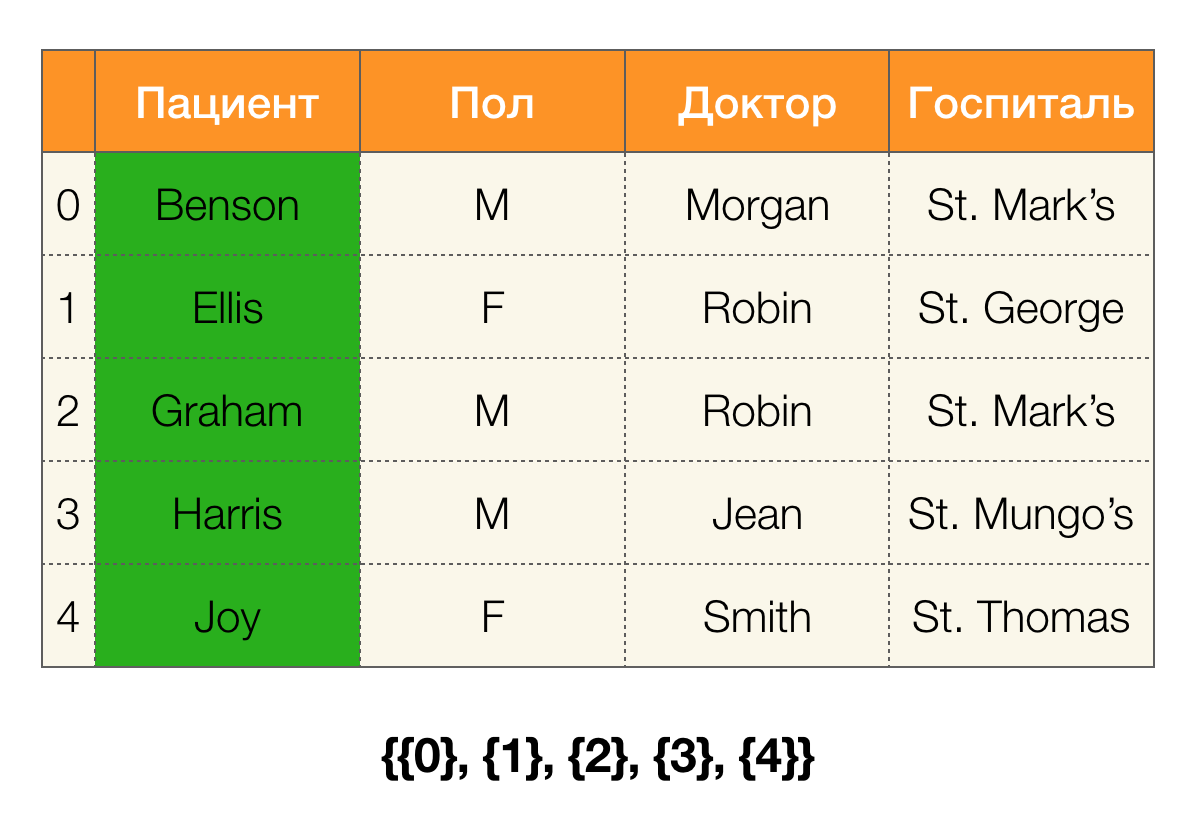
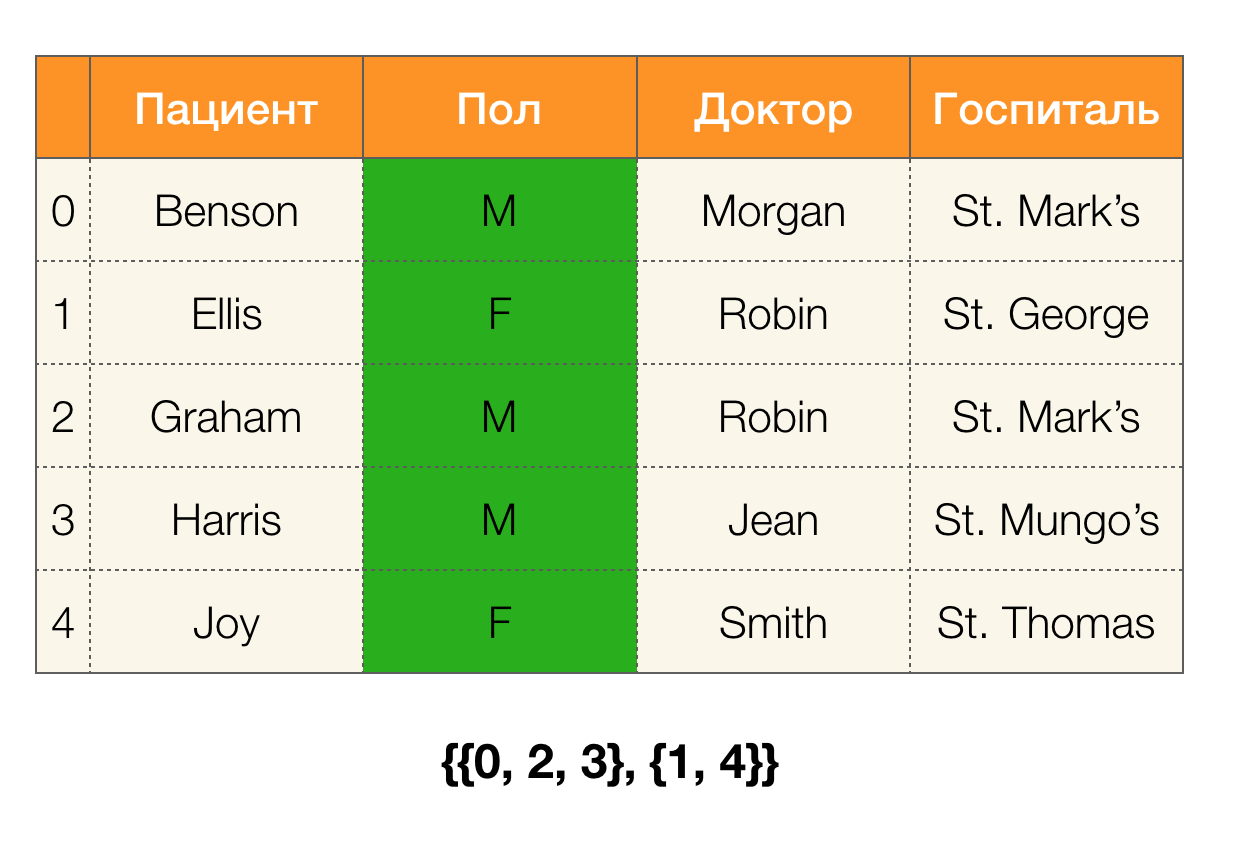
Selain itu, sesuai dengan definisi, partisi untuk kolom Pasien akan benar-benar kosong, karena satu cluster dikeluarkan dari partisi.

Partisi dapat diperoleh dengan beberapa atribut. Dan untuk ini ada dua cara: melalui tabel, membangun partisi sekaligus sesuai dengan semua atribut yang diperlukan, atau membangunnya menggunakan operasi partisi crossing sepanjang subset atribut. Algoritma pencarian FZ menggunakan opsi kedua.

Dengan kata-kata sederhana, misalnya, untuk mendapatkan partisi berdasarkan kolom ABC , Anda dapat mengambil partisi untuk AC dan B (atau himpunan bagian himpunan terpisah yang lain) dan memotongnya satu sama lain. Operasi persimpangan dua partisi mengidentifikasi kelompok dengan panjang terbesar yang umum untuk kedua partisi.

Mari kita lihat sebuah contoh:





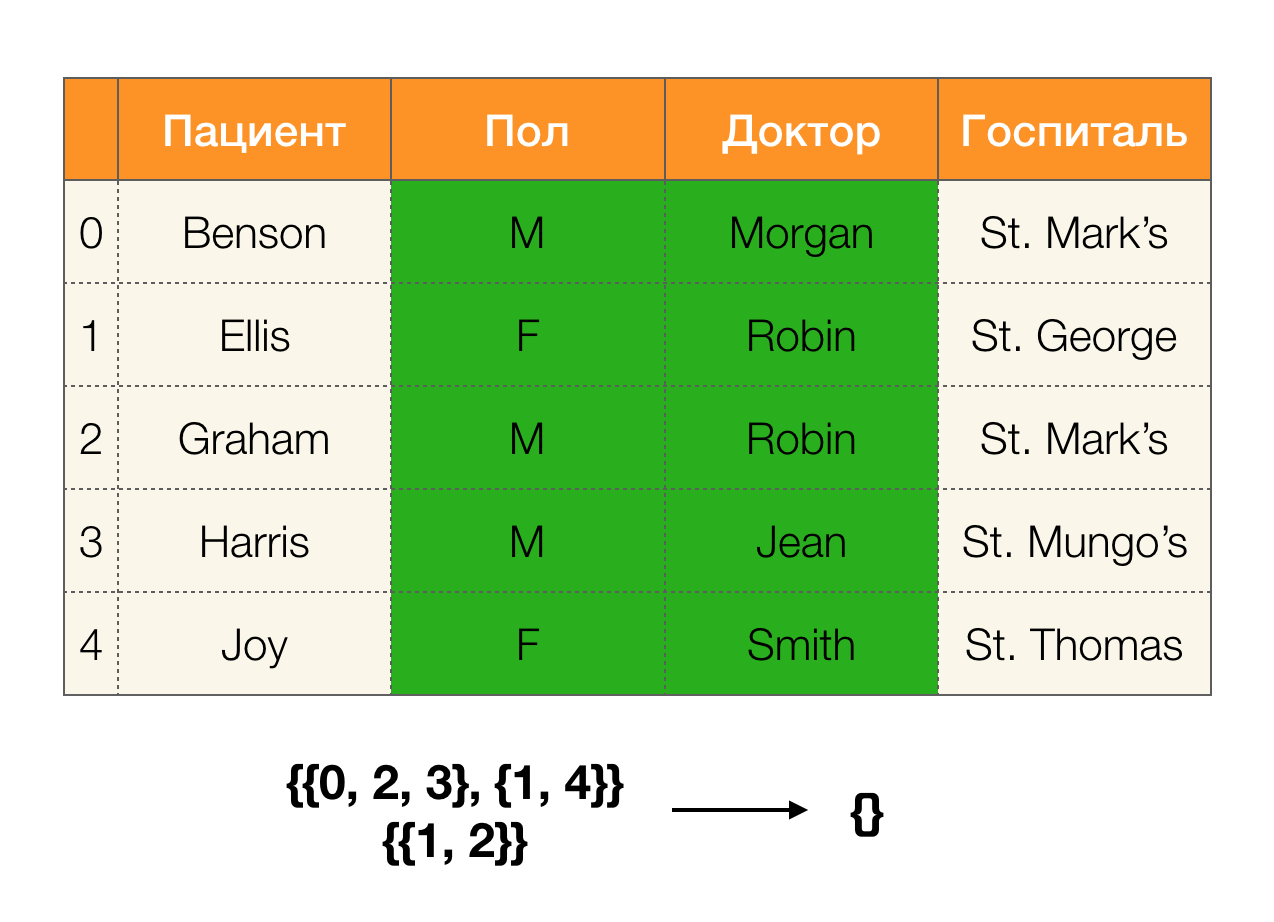
Dalam kasus pertama, kami menerima partisi kosong. Jika Anda melihat dengan seksama pada tabel, maka memang, nilai-nilai identik untuk dua atribut tidak ada di sana. Jika kita sedikit memodifikasi tabel (kasing di sebelah kanan), maka kita sudah mendapatkan persimpangan yang kosong. Pada saat yang sama, baris 1 dan 2 benar-benar berisi nilai yang sama untuk atribut Paul dan Doctor .

Selanjutnya, kita membutuhkan konsep seperti ukuran partisi. Secara formal:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

Sederhananya, ukuran partisi adalah jumlah cluster yang termasuk dalam partisi (ingat bahwa masing-masing cluster tidak termasuk dalam partisi!):





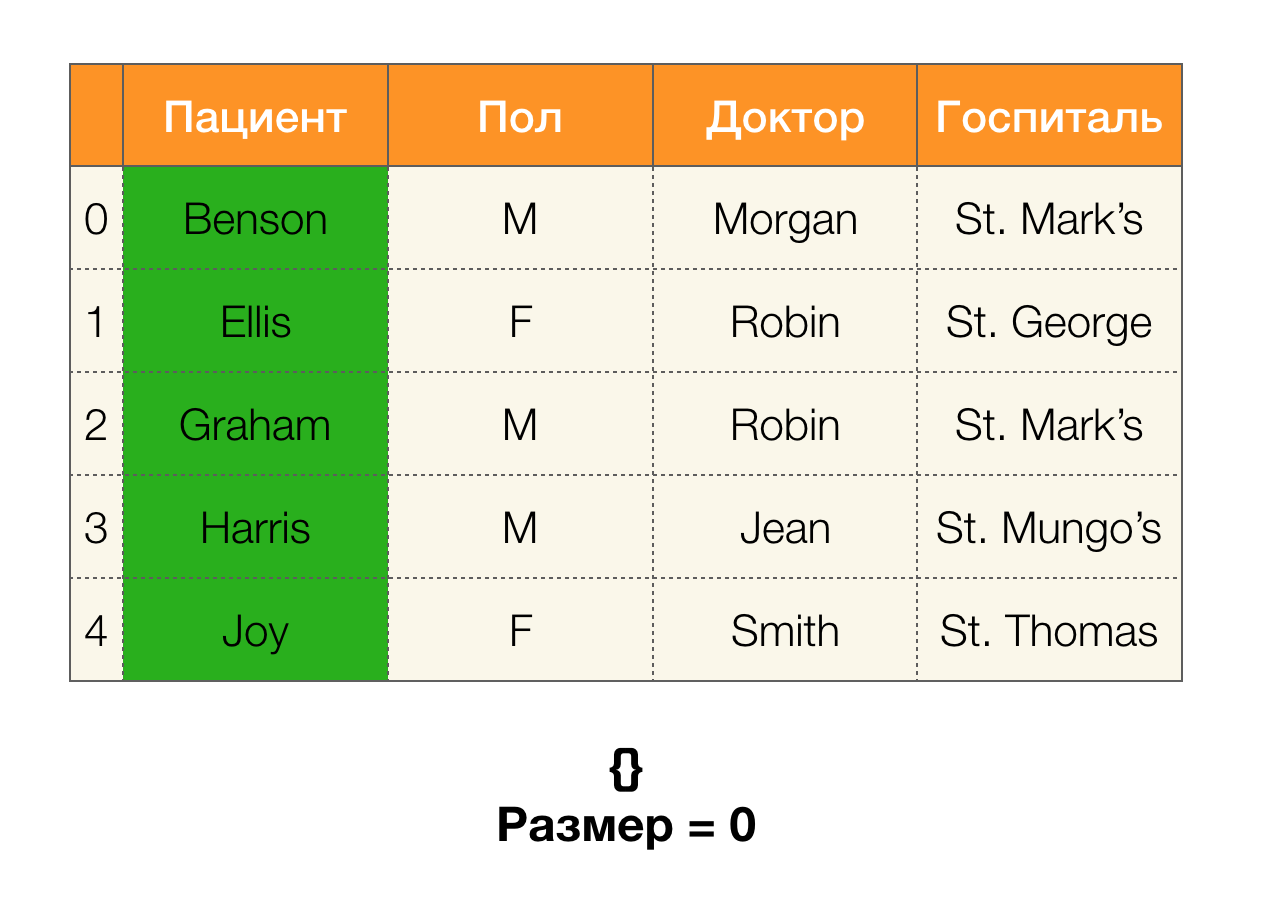
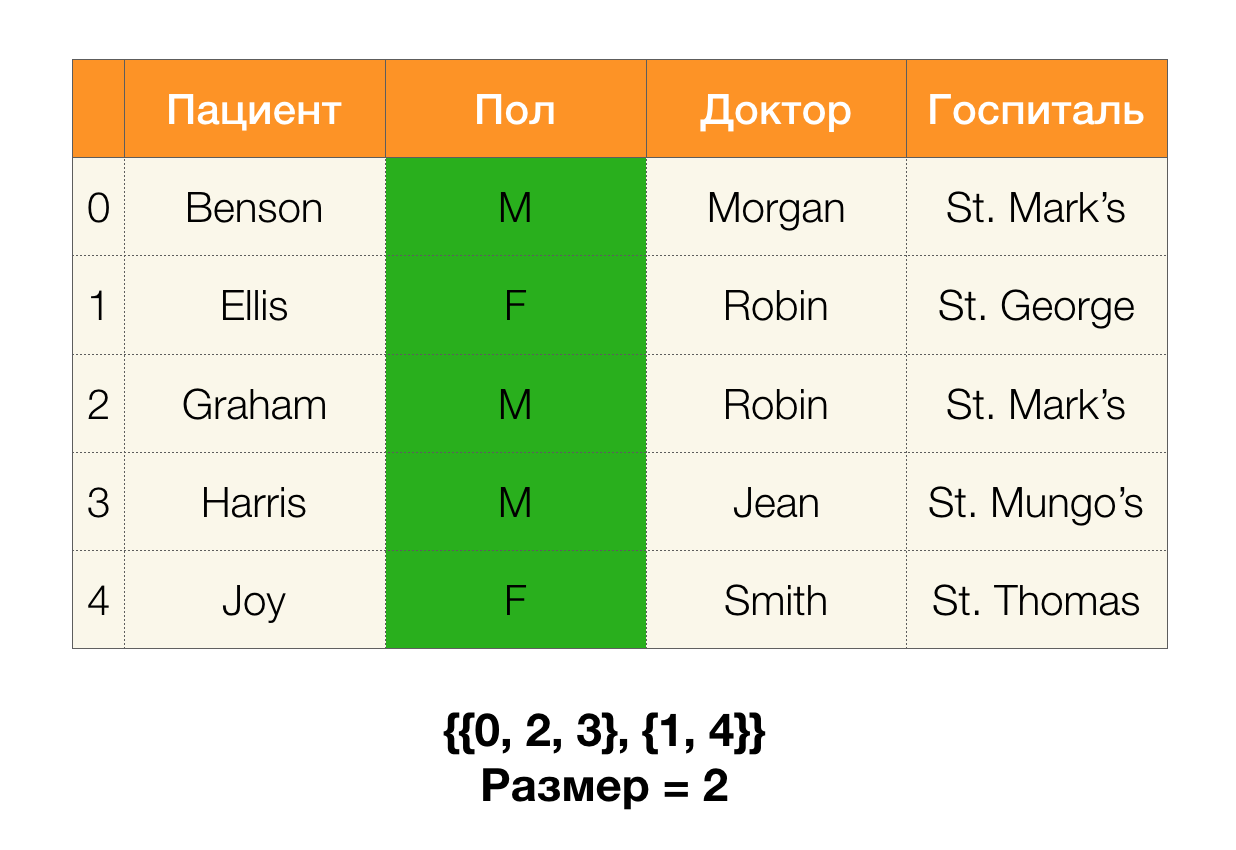
Sekarang kita dapat mendefinisikan salah satu lemma kunci, yang untuk partisi yang diberikan memungkinkan kita untuk menentukan apakah ketergantungan dipegang atau tidak:

Lemma 1 . Ketergantungan A, B → C ditahan jika dan hanya jika

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

Menurut lemma, untuk menentukan apakah suatu ketergantungan diadakan, perlu untuk melakukan empat langkah:

1. Hitung partisi untuk sisi kiri ketergantungan
2. Hitung partisi untuk sisi kanan ketergantungan
3. Hitung produk langkah pertama dan kedua
   
4. Bandingkan ukuran partisi yang diperoleh pada langkah pertama dan ketiga
   

Berikut ini adalah contoh memeriksa apakah ketergantungan dipertahankan oleh lemma ini:






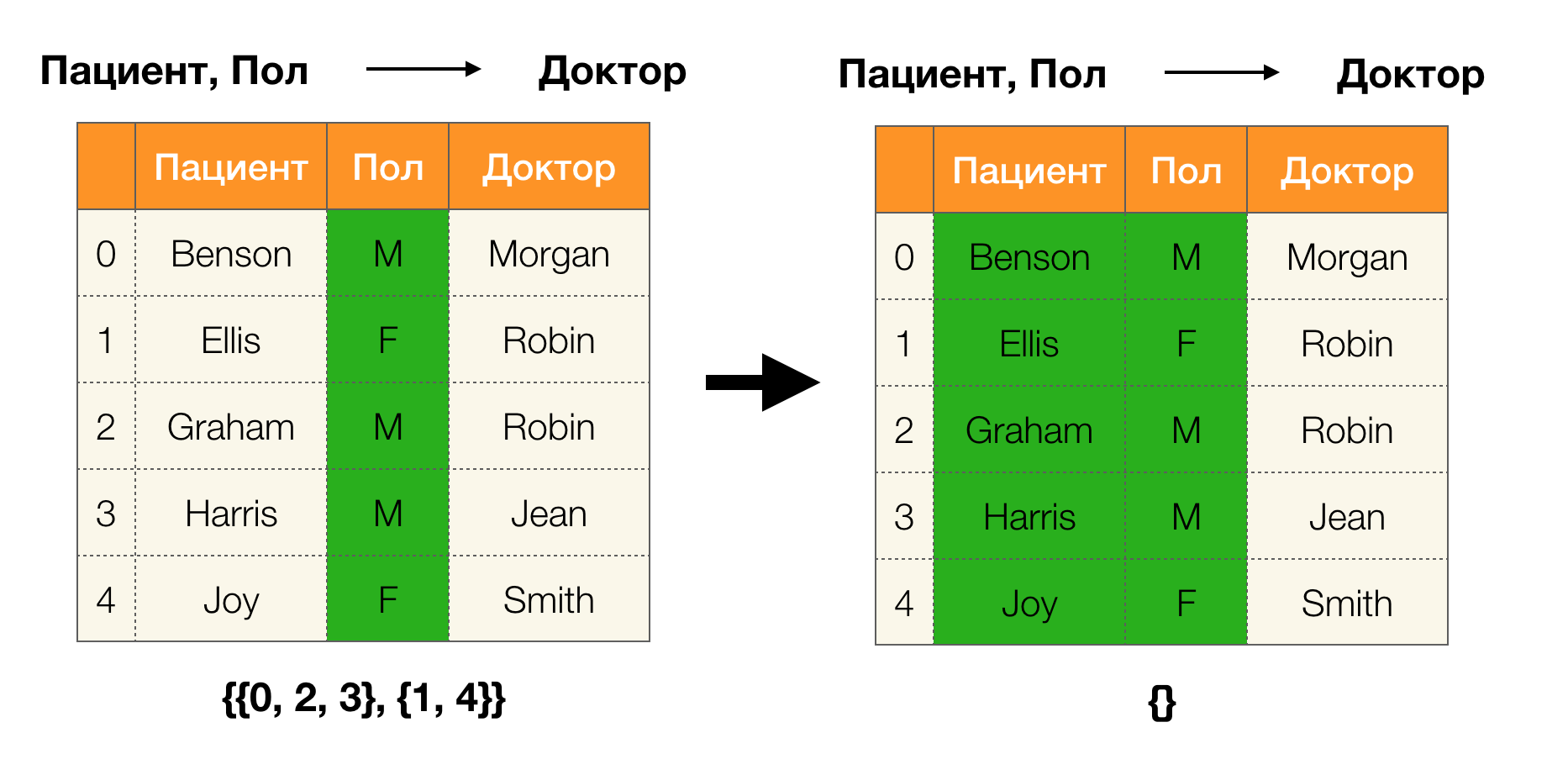
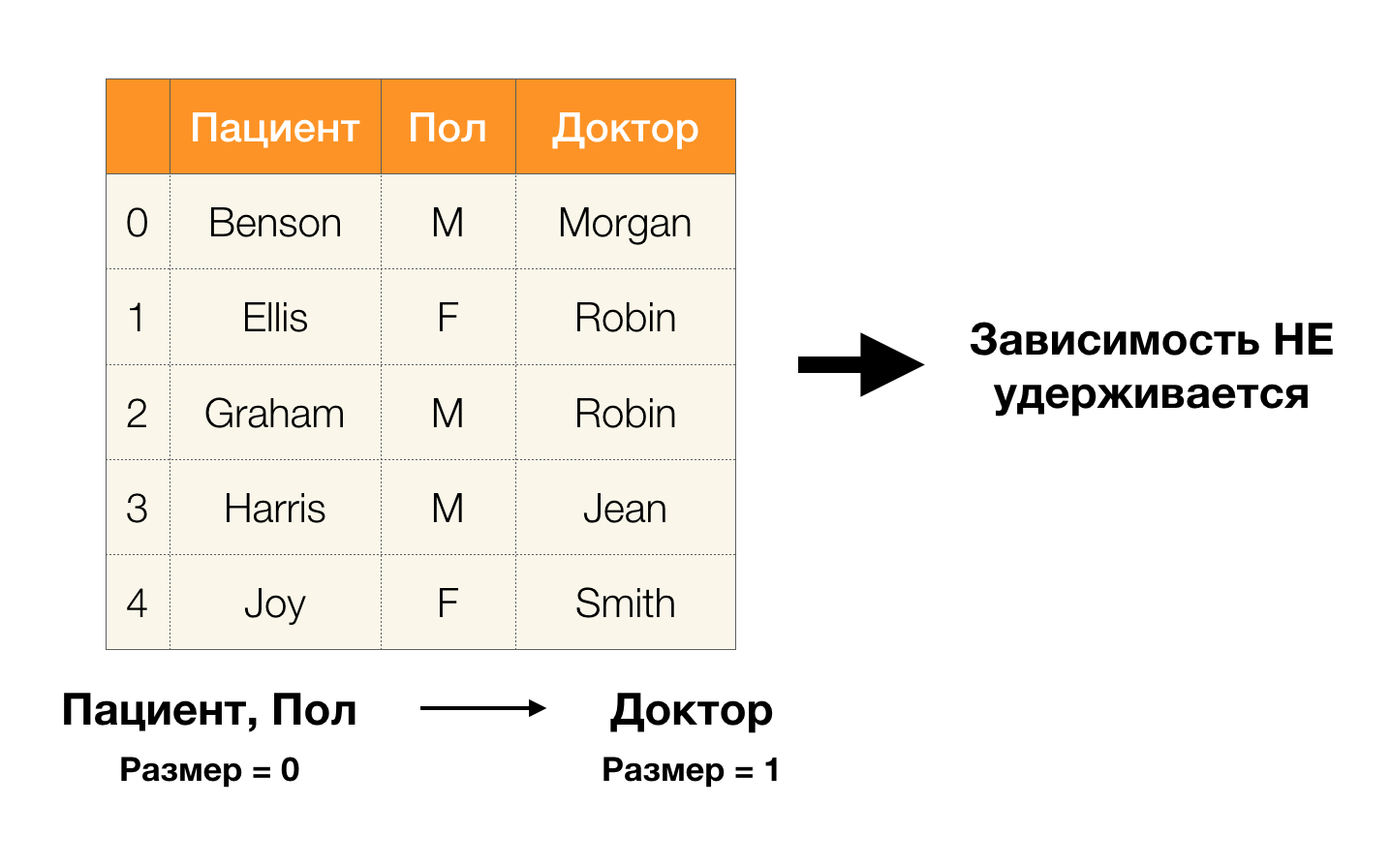
Dalam artikel ini, kami menguji konsep-konsep seperti ketergantungan fungsional, perkiraan ketergantungan fungsional, memeriksa di mana mereka digunakan, serta algoritma pencarian untuk Hukum Federal yang ada. Kami juga memeriksa secara rinci konsep dasar, tetapi penting yang secara aktif digunakan dalam algoritma modern untuk mencari Hukum Federal.

Referensi literatur:

1. Huhtala Y. et al. TANE: Algoritma yang efisien untuk menemukan dependensi fungsional dan perkiraan // Jurnal komputer. - 1999. - T. 42. - Tidak. 2. - S. 100-111.
2. Kruse S., Naumann F. Penemuan efisien dependensi perkiraan // Prosiding Endowment VLDB. - 2018. - T. 11. - Tidak. 7. - S. 759-772.
3. Papenbrock T., Naumann F. Pendekatan hybrid untuk penemuan ketergantungan fungsional // Prosiding Konferensi Internasional 2016 tentang Manajemen Data. - ACM, 2016 .-- S. 821-833.
4. Papenbrock T. et al. Penemuan ketergantungan fungsional: Evaluasi eksperimental tujuh algoritma // Prosiding Endowment VLDB. - 2015. - T. 8. - No. 10. - S. 1082-1093.
5. Kumar A. et al. Untuk bergabung atau tidak bergabung?: Berpikir dua kali tentang bergabung sebelum pemilihan fitur // Prosiding Konferensi Internasional 2016 tentang Pengelolaan Data. - ACM, 2016 .-- S. 19-34.
6. Abo Khamis M. et al. Pembelajaran dalam-basis data dengan tensor jarang / // Prosiding Simposium ACM SIGMOD-SIGACT-SIGAI ke-37 tentang Prinsip-prinsip Sistem Basis Data. - ACM, 2018 .-- S. 325-340.
7. Hellerstein JM et al. Pustaka analitik MADlib: atau keterampilan MAD, SQL // Proceedings of VLDB Endowment. - 2012. - T. 5. - No. 12. - S. 1700-1711.
8. Qin C., Rusu F. Perkiraan spekulatif untuk optimasi penurunan gradien terdistribusi terascale // Prosiding Workshop Keempat tentang analisis data di Cloud. - ACM, 2015 .-- S. 1.
9. Meng X. et al. Mllib: Pembelajaran mesin di apache spark // The Journal of Machine Learning Research. - 2016. - T. 17. - No. 1 .-- S. 1235-1241.

Penulis artikel: Anastasia Birillo , peneliti di JetBrains Research , siswa dari pusat CS dan Nikita Bobrov , peneliti di JetBrains Research