Analisis terperinci dari metode simpleks

Prolog

Baru-baru ini, ada kebutuhan untuk membuat program dari awal yang mengimplementasikan algoritma metode simpleks. Tetapi dalam perjalanan solusinya, saya mengalami masalah: tidak ada begitu banyak sumber daya di Internet di mana Anda dapat melihat analisis teoretis terperinci dari algoritma tersebut (alasannya: mengapa kami mengambil langkah-langkah ini atau itu) dan tips implementasi praktis - langsung, algoritma. Kemudian saya membuat janji pada diri sendiri - segera setelah saya menyelesaikan tugas, saya akan menulis posting saya tentang topik ini. Sebenarnya, kita akan membicarakan ini.

Komentar. Posting akan ditulis dalam bahasa yang cukup formal, tetapi akan diberikan komentar, yang akan memberikan kejelasan. Format seperti itu akan mempertahankan pendekatan ilmiah dan, pada saat yang sama, dapat membantu beberapa orang dalam mempelajari masalah ini.

§1. Pernyataan masalah pemrograman linier

Definisi: Pemrograman linier adalah disiplin matematik yang ditujukan untuk teori dan metode penyelesaian masalah ekstrem pada set ruang n-dimensi yang didefinisikan oleh sistem persamaan linear dan ketidaksetaraan.

Tugas umum pemrograman linier (selanjutnya - LP) memiliki bentuk:

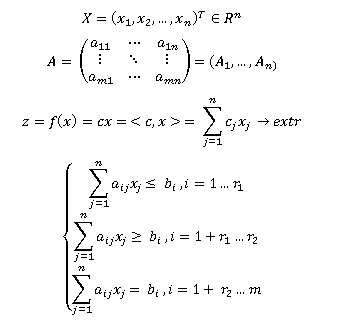
§2. Bentuk kanonik dari masalah LP

Bentuk kanonik masalah LP:



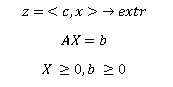Catatan: Setiap masalah LP berkurang menjadi kanonik.

Algoritma untuk transisi dari masalah LP acak ke bentuk kanonik:

1. Ketidaksetaraan dengan negatif$$ $ inline $ b_i $ inline $ kalikan dengan (-1).
2. Jika ketimpangan bentuk (≤), maka tambahkan ke sisi kiri$$ $ inline $ s_i $ inline $ Merupakan variabel tambahan, dan kami memperoleh kesetaraan.
3. Jika ketimpangan bentuk (≥), maka kurangi dari sisi kiri$$ $ inline $ s_i $ inline $ , dan kami memperoleh kesetaraan.
4. Kami melakukan penggantian variabel:

• Jika$$ $ inline $ x_i ≤ 0 $ inline $ lalu$$ $ inline $ x_i '= -x_i ≥ 0 $ inline $
• Jika$$ $ inline $ x_i $ inline $ - apa saja$$ $ inline $ x_i = x_i '- x_i' '$ inline $ dimana$$ $ inline $ x_i ', x_i''≥ $ $ inline $

Catatan: Kami akan memberi nomor$$ $ inline $ s_i $ inline $ oleh nomor ketimpangan yang kami tambahkan itu.

Catatan:$$ $ inline $ s_i $ inline $ ≥0.

§3. Poin sudut. Variabel dasar / gratis. Solusi dasar

Definisi: Poin$$ $ inline $ X ∈ D $ inline $ disebut titik sudut jika representasi$$ $ inline $ X = αX ^ 1 + (1-α) X ^ 2, di mana X ^ 1, X ^ 2 ∈ D; 0 <α <1 $ inline $ hanya mungkin dengan$$ $ inline $ X ^ 1 = X ^ 2 $ inline $ .

Dengan kata lain, tidak mungkin untuk menemukan dua titik di wilayah tersebut, interval yang melewati yang berisi$$ $ inline $ X $ inline $ (mis.$$ $ inline $ X $ inline $ Bukan titik internal).

Metode grafis untuk memecahkan masalah LP menunjukkan bahwa menemukan solusi optimal dikaitkan dengan titik sudut. Ini adalah konsep dasar ketika mengembangkan metode simpleks.

Definisi: Biarkan ada sistem persamaan m dan n tidak diketahui (m <n). Kami membagi variabel menjadi dua set: (nm) kami menetapkan variabel sama dengan nol, dan variabel m yang tersisa ditentukan dengan memecahkan sistem persamaan awal. Jika solusi ini unik, maka variabel bukan nol disebut dasar; nol (nm) variabel - bebas (non-dasar), dan nilai-nilai yang dihasilkan dari variabel disebut solusi dasar.

§4. Metode simpleks

Metode simpleks memungkinkan Anda untuk secara efektif menemukan solusi optimal, menghindari penghitungan sederhana dari semua titik sudut yang mungkin. Prinsip utama metode ini: perhitungan dimulai dengan semacam solusi dasar "mulai", dan kemudian pencarian dilakukan untuk solusi yang "meningkatkan" nilai fungsi tujuan. Ini hanya mungkin jika peningkatan dalam beberapa variabel mengarah pada peningkatan nilai fungsional.

Prasyarat untuk menerapkan metode simpleks:

1. Tugas harus memiliki bentuk kanonik.
2. Tugas harus memiliki dasar yang eksplisit.

Definisi: Basis yang dipilih secara eksplisit adalah vektor dari bentuk:$$ $ inline $ (.. 0100 ..) ^ T, (..010 ..) ^ T, (.. 0010 ..) ^ T ... $ inline $ , yaitu hanya satu koordinat vektor yang bukan nol dan sama dengan 1.

Catatan: Vektor dasar memiliki dimensi (m * 1), di mana m adalah jumlah persamaan dalam sistem kendala.

Untuk kenyamanan perhitungan dan visualisasi, tabel simpleks biasanya digunakan:

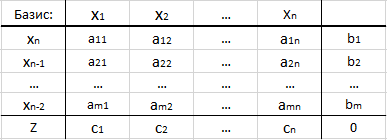
• Baris pertama menunjukkan "nama" semua variabel.
• Di kolom pertama, jumlah variabel dasar ditunjukkan, dan di sel terakhir, huruf Z (ini adalah garis fungsional).
• Di "tengah tabel" menunjukkan koefisien dari matriks kendala - aij.
• Kolom terakhir adalah vektor sisi kanan persamaan yang sesuai dari sistem kendala.
• Sel paling kanan adalah nilai fungsi objektif. Pada iterasi pertama, diasumsikan 0.

Catatan: Basis adalah variabel, koefisien dalam matriks batasan yang membentuk vektor basis.

Catatan: Jika kendala dalam masalah asli diwakili oleh ketidaksetaraan bentuk ≤, maka ketika masalah dikurangi menjadi bentuk kanonik, variabel tambahan yang diperkenalkan membentuk solusi dasar awal.

Catatan: Koefisien pada garis fungsional diambil dengan tanda "-".

Algoritma Metode Simpleks:

1. Pilih variabel yang akan kami perkenalkan dalam basis. Ini dilakukan sesuai dengan prinsip yang ditunjukkan sebelumnya: kita harus memilih variabel yang kenaikannya akan mengarah pada peningkatan fungsional. Pemilihan dilakukan sesuai dengan aturan berikut:

• Jika tugas minimal, pilih elemen positif maksimum di baris terakhir.
• Jika tugas maksimal, pilih negatif minimum.

Pilihan semacam itu, pada kenyataannya, sesuai dengan prinsip yang disebutkan di atas: jika tugasnya minimal, maka semakin besar jumlah yang kita kurangi, semakin cepat fungsionalnya berkurang; untuk maksimum, sebaliknya - semakin besar angka yang ditambahkan, semakin cepat fungsional tumbuh.

Catatan: Meskipun kita mengambil angka negatif minimum dalam masalah ke maksimum, koefisien ini menunjukkan arah pertumbuhan fungsional, karena garis fungsional dalam tabel simpleks diambil dengan tanda "-". Situasi serupa dengan minimisasi.

Definisi: Kolom tabel simpleks yang sesuai dengan koefisien yang dipilih disebut kolom terkemuka .

2. Pilih variabel yang akan kami perkenalkan dalam basis. Untuk melakukan ini, Anda perlu menentukan variabel dasar mana yang paling mungkin hilang ketika variabel dasar baru tumbuh. Secara aljabar, ini dilakukan sebagai berikut:

• Vektor bagian kanan dibagi oleh kolom terminating
• Di antara nilai yang diperoleh pilih minimum positif (jawaban negatif dan nol tidak dipertimbangkan)

Definisi: Garis tersebut disebut garis depan dan berhubungan dengan variabel yang akan diturunkan dari basis.

Catatan: Faktanya, kami menyatakan variabel basis lama dari setiap persamaan sistem kendala melalui variabel-variabel lainnya dan melihat persamaan mana yang kemungkinan besar akan memberikan peningkatan variabel basis baru 0. Dengan memasuki situasi ini berarti kita "tersandung" pada sebuah simpul baru. Itu sebabnya nol dan elemen negatif tidak dipertimbangkan, karena Memperoleh hasil seperti itu berarti bahwa pilihan variabel basis yang baru akan membawa kita menjauh dari area di mana tidak ada solusi.

3. Kami mencari elemen yang berdiri di persimpangan baris dan kolom terkemuka.

Definisi: Unsur seperti itu disebut unsur utama .

4. Alih-alih variabel yang akan dikecualikan, di kolom pertama (dengan nama-nama variabel dasar), tulis nama variabel yang kita masukkan ke dalam basis.

5. Selanjutnya, proses penghitungan solusi dasar baru dimulai. Itu terjadi menggunakan metode Jordan-Gauss .

• Lead Line Baru = Lead Line Lama / Lead
• Baris baru = Baris baru - Faktor baris di kolom terkemuka * Baris baru

Catatan: Konversi semacam ini bertujuan untuk memperkenalkan variabel yang dipilih ke dalam basis, mis. representasi kolom utama sebagai vektor dasar.

6. Setelah itu, kami memeriksa kondisi optimalitas. Jika solusi yang dihasilkan tidak optimal, ulangi seluruh proses lagi.

§5. Interpretasi hasil dari metode simpleks

1. Optimalitas

Kondisi optimalitas untuk solusi yang dihasilkan:

• Jika tugas maksimum, tidak ada koefisien negatif pada baris fungsional (mis., Dengan perubahan variabel apa pun, nilai fungsional yang dihasilkan tidak akan tumbuh).
• Jika tugas minimal, tidak ada koefisien positif pada baris fungsional (mis., Dengan perubahan apa pun dalam variabel, nilai fungsional yang dihasilkan tidak akan berkurang).

2. Fungsionalitas tidak terbatas

Namun, perlu dicatat bahwa fungsional yang diberikan mungkin tidak mencapai maksimum / minimum di area tertentu. Atribut aljabar ini dapat dirumuskan sebagai berikut:

Ketika memilih baris terdepan (variabel yang akan dikecualikan), hasil pembagian termwise dari vektor sisi kanan oleh kolom terkemuka hanya berisi nilai nol dan negatif.

Faktanya, ini berarti bahwa tidak peduli apa pun pertumbuhan yang kami tetapkan, variabel dasar baru, kami tidak akan pernah menemukan titik baru. Jadi, fungsi kami tidak terbatas pada serangkaian solusi yang layak.

3. Solusi alternatif

Ketika menemukan solusi optimal, opsi lain dimungkinkan - ada solusi alternatif (titik sudut lain yang memberikan nilai fungsional yang sama).

Tanda aljabar adanya alternatif:

Setelah mencapai solusi optimal, ada nol koefisien untuk variabel bebas di baris fungsional.

Ini berarti bahwa dengan pertumbuhan variabel yang sesuai dengan koefisien nol, nilai fungsional tidak akan berubah dan solusi dasar baru juga akan memberikan fungsi optimal.

Epilog

Artikel ini ditujukan untuk pemahaman yang lebih dalam tentang bagian teoretis. Dalam komentar dan penjelasan di sini Anda bisa mendapatkan jawaban atas pertanyaan yang biasanya dihilangkan ketika mempelajari metode ini dan mengambil apriori. Namun, kita harus memahami bahwa banyak metode optimasi numerik didasarkan pada metode simpleks (misalnya, metode Gomori , Metode - M ) dan tanpa pemahaman mendasar, tidak mungkin banyak kemajuan dapat dibuat dalam studi lebih lanjut dan penerapan semua algoritma dari kelas ini.

Beberapa saat kemudian saya akan menulis artikel tentang implementasi praktis dari metode simpleks, serta beberapa artikel tentang Metode Variabel Buatan (Metode-M), Metode Gomori dan Metode Cabang dan Perbatasan.

Terima kasih atas perhatian anda!

PS

Jika Anda sudah tersiksa oleh penerapan metode simpleks, saya menyarankan Anda untuk membaca buku oleh A. Taha Pengantar studi operasi - semuanya dianalisis dengan baik di sana, baik secara teori maupun dalam contoh; dan juga lihat contoh pemecahan masalah matburo.ru - ini akan membantu implementasi kode.