Buku Alan Turing dan Catatan Misterius - Detektif Sains

Terjemahan asli di blog saya

Bagaimana buku ini sampai ke saya?

Pada bulan Mei 2017, saya menerima email dari guru lama saya di sekolah tinggi bernama George Rutter, di mana ia menulis: “ Saya memiliki salinan buku Dirac Jerman yang besar (Die Prinzipien der Quantenmechanik), yang milik Alan Turing, dan setelahnya ketika saya membaca buku Anda Pembuat Ide , bagi saya tampaknya begitu saja bahwa Anda adalah orang yang membutuhkannya . " Dia menjelaskan kepada saya bahwa dia telah menerima buku dari yang lain (saat itu sudah meninggal) guru sekolah saya Norman Rutledge , tentang siapa saya tahu bahwa dia adalah teman Alan Turing. George mengakhiri suratnya dengan frasa: " Jika Anda membutuhkan buku ini, saya bisa menyerahkannya kepada Anda saat Anda datang ke Inggris nanti ."

Setelah beberapa tahun pada bulan Maret 2019, saya benar-benar tiba di Inggris, setelah itu saya setuju dengan George untuk bertemu untuk sarapan di sebuah hotel kecil di Oxford. Kami makan, mengobrol, dan menunggu makanan selesai. Kemudian tibalah saat yang tepat untuk membahas buku itu. George memasukkan tangannya ke dalam kopernya dan mengeluarkan volume akademik tipikal yang dirancang dengan sederhana pada pertengahan tahun 1900-an.



Saya membuka sampulnya, bertanya-tanya apakah itu ada di bagian belakang tulisan: " Properti Alan Turing" atau semacamnya. Tapi, sayangnya, ini bukan masalahnya. Namun demikian, catatan yang agak ekspresif pada empat lembar dari Norman Rutledge ke George Rutter, yang ditulis pada tahun 2002, melekat padanya.

Saya mengenal Norman Rutledge ketika saya masih seorang siswa sekolah menengah di Eton pada awal 1970-an. Dia adalah seorang guru matematika yang dijuluki The Nutty Norman. Dia adalah seorang guru yang menyenangkan dalam segala hal dan menceritakan kisah tanpa akhir tentang matematika dan segala macam hal menarik lainnya. Dia bertanggung jawab untuk memastikan bahwa sekolah menerima komputer (diprogram dengan selotip selebar meja) - ini adalah komputer pertama yang pernah saya gunakan .

Pada masa itu, saya tidak tahu apa-apa tentang masa lalu Norman (ingat bahwa ini jauh sebelum munculnya Internet). Saya hanya tahu bahwa dia adalah "Dr. Rutledge." Dia sering bercerita tentang orang-orang dari Cambridge, tetapi dalam ceritanya dia tidak pernah menyebut Alan Turing. Tentu saja, Turing tidak cukup terkenal saat itu (walaupun, ternyata, saya sudah mendengar tentang dia dari seseorang yang mengenalnya di Bletchley Park (mansion di mana pusat enkripsi terletak selama Perang Dunia II)).

Alan Turing tidak terkenal sampai 1981, ketika saya pertama kali mulai mempelajari program-program sederhana , meskipun saat itu dalam konteks automata seluler, dan bukan mesin Turing .

Tiba-tiba, suatu hari, melihat katalog kartu di perpustakaan California Institute of Technology , saya menemukan buku Alan M. Turing , yang ditulis oleh ibunya Sarah Turing. Buku ini memiliki banyak informasi, termasuk karya ilmiah Turing yang tidak dipublikasikan tentang biologi. Namun, saya tidak belajar apa-apa tentang hubungannya dengan Norman Rutledge, karena buku itu tidak menyebutkan apa-apa tentang dia (walaupun, ketika saya tahu, Sarah Turing berkorespondensi dengan Norman tentang buku ini , dan Norman bahkan menulis ulasannya pada akhirnya).



Sepuluh tahun kemudian, disetel dengan rasa ingin tahu yang ekstrem untuk Turing dan pekerjaan biologinya (yang saat itu tidak diterbitkan), saya mengunjungi arsip Turing di King's College, Cambridge . Segera, setelah membiasakan diri dengan apa yang mereka miliki dari pekerjaan Turing, dan setelah menghabiskan waktu di sana, saya berpikir bahwa pada saat yang sama saya dapat memintanya untuk melihat korespondensi pribadinya juga. Melihat melalui itu, saya menemukan beberapa surat dari Alan Turing ke Norman Rutledge.

Pada saat itu, biografi Andrew Hodges diterbitkan, yang telah melakukan begitu banyak sehingga Turing akhirnya menjadi terkenal, itu menegaskan bahwa Alan Turing dan Norman Rutledge benar-benar berteman, dan juga bahwa Turing adalah konsultan ilmiah untuk Norman. Saya ingin bertanya kepada Rutledge tentang Turing, tetapi pada saat itu Norman sudah pensiun dan menjalani kehidupan yang terpencil. Namun, ketika saya menyelesaikan pekerjaan pada buku A New Kind of Science pada tahun 2002 (setelah retret sepuluh tahun saya), saya melacaknya dan mengiriminya salinan buku dengan tulisan, "Kepada Guru Matematika Terakhir Saya." Kemudian kami berkorespondensi sedikit, dan pada tahun 2005 saya kembali ke Inggris dan setuju untuk bertemu dengan Norman untuk minum teh di sebuah hotel mewah di London pusat.

Kami telah berbicara baik tentang banyak hal, termasuk Alan Turing. Norman memulai percakapan kami dengan kisah yang benar-benar ia kenal Turing, kebanyakan secara dangkal, 50 tahun lalu. Namun demikian, dia punya sesuatu untuk diceritakan tentang dia secara pribadi: " Dia tidak ramah ." " Dia banyak terkikik ." " Dia tidak bisa benar-benar berbicara dengan non-ahli matematika ." " Dia selalu takut mengecewakan ibunya ." " Dia pergi siang hari dan berlari maraton ." " Dia tidak terlalu ambisius ." Kemudian pembicaraan kembali ke identitas Norman. Dia mengatakan bahwa terlepas dari kenyataan bahwa dia sudah pensiun selama 16 tahun, dia masih menulis artikel untuk Surat Kabar Matematika , sehingga, dalam kata-katanya, "untuk menyelesaikan semua karya ilmiahnya sebelum pindah ke dunia lain " , di mana, ketika dia menambahkan dengan senyum yang nyaris tak terlihat, " semua kebenaran matematika pasti akan terungkap ." Ketika pesta teh selesai, Norman mengenakan jaket kulitnya dan menuju mopednya, sama sekali mengabaikan ledakan yang mengganggu lalu lintas di London pada hari itu.

Ini adalah terakhir kali saya melihat Norman, dia meninggal pada 2013.

Enam tahun kemudian, saya duduk sarapan bersama George Rutter. Bersama saya adalah catatan dari Rutledge, yang ditulis olehnya pada tahun 2002 dalam tulisan tangannya yang khas:



Awalnya saya membaca surat itu dengan lancar. Dia ekspresif seperti biasa:

Saya menerima sebuah buku karya Alan Turing dari teman dan pengeksekusinya Robin Gandy (di King's College, adalah normal untuk memberikan buku-buku dari koleksi rekan-rekan yang telah meninggal, dan saya memilih koleksi puisi oleh A.E. Pengurus rumah tangga dari buku-buku Ivor Ramsey sebagai hadiah yang cocok (dia adalah dekan dan melompat dari kapel [tahun 1956]) ...

Kemudian dalam sebuah catatan singkat ia menulis:

Anda bertanya di mana, pada akhirnya, buku ini seharusnya - menurut pendapat saya, buku itu harus diberikan kepada seseorang yang menghargai segala sesuatu yang berkaitan dengan pekerjaan Turing, jadi nasibnya tergantung pada Anda.

Stephen Wolfram mengirimi saya bukunya yang mengesankan, tetapi saya tidak cukup menyelami buku itu ...

Sebagai kesimpulan, ia mengucapkan selamat kepada George Rutter karena memiliki keberanian untuk pindah (ternyata, sementara) ke Australia setelah pensiun, dengan mengatakan bahwa ia sendiri akan " bermain pindah ke Sri Lanka sebagai contoh kehidupan yang murah dan seperti lotus, " tetapi menambahkan bahwa " peristiwa yang terjadi di sana sekarang menunjukkan bahwa ia seharusnya tidak melakukan ini " (tampaknya merujuk pada perang saudara di Sri Lanka).

Jadi apa yang tersembunyi di perut buku ini?

Jadi, apa yang telah saya lakukan dengan salinan buku berbahasa Jerman yang ditulis oleh Paul Dirac yang dulunya milik Alan Turing. Saya tidak membaca bahasa Jerman, tetapi saya memiliki salinan buku yang sama dalam bahasa Inggris (yang merupakan bahasa aslinya) dari edisi tahun 1970-an. Namun demikian, sekali saat sarapan, saya merasa benar bahwa saya harus dengan cermat meninjau halaman buku demi halaman. Pada akhirnya, ini adalah praktik umum ketika berhadapan dengan buku-buku antik.

Perlu dicatat bahwa saya terkesan dengan keanggunan presentasi Dirac. Buku ini diterbitkan pada tahun 1931, tetapi formalisme murni (dan, ya, terlepas dari kendala bahasa, saya dapat membaca matematika yang dijelaskan dalam buku ini) hampir sama seperti jika ditulis hari ini. (Saya tidak ingin terlalu fokus pada Dirac di sini, tetapi teman saya Richard Feynman mengatakan kepada saya bahwa, setidaknya menurut pendapatnya, eksposisi Dirac adalah bersuku kata satu. Norman Rutledge mengatakan kepada saya bahwa ia berteman di Cambridge dengan putra angkat Dirac , yang menjadi ahli teori dalam Norman cukup sering berada di rumah Dirac dan mengatakan bahwa "pria hebat" kadang-kadang secara pribadi menghilang ke latar belakang, sedangkan latar depan selalu memiliki banyak teka-teki matematika. Sayangnya, saya sendiri belum pernah bertemu Paul Dirac, meskipun Saya diberitahu bahwa setelah t wow, ketika dia akhirnya meninggalkan Cambridge dan pergi ke Florida, dia kehilangan sebagian besar kekakuannya sebelumnya dan menjadi orang yang sangat ramah).

Tetapi kembali ke buku Dirac, yang milik Turing. Di halaman 9, saya perhatikan garis bawah dan catatan margin kecil yang ditulis dengan pensil sederhana. Saya terus membalik halaman. Setelah beberapa bab, catatan itu menghilang. Tapi kemudian, tiba-tiba, saya menemukan catatan yang tertanam di halaman 127 dengan konten berikut:



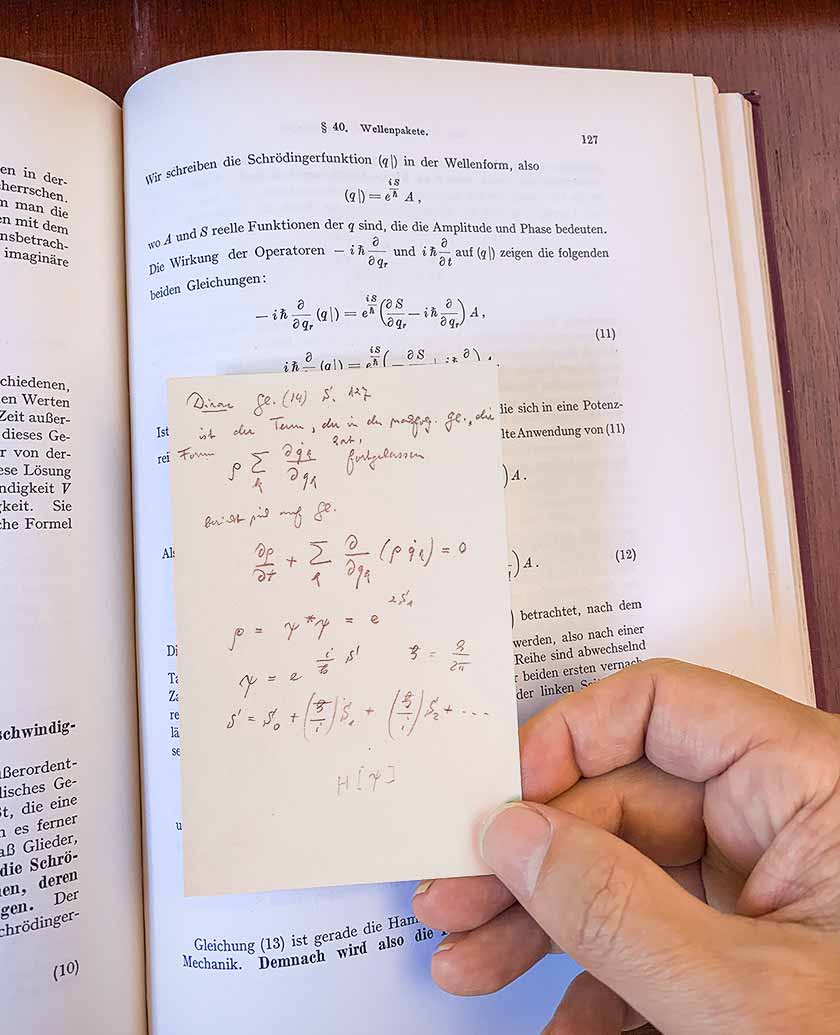
Itu ditulis dalam bahasa Jerman dalam tulisan tangan standar Jerman. Dan sepertinya itu entah bagaimana bisa dihubungkan dengan mekanika Lagrangian . Saya pikir mungkin seseorang memiliki buku ini sebelum Turing, dan ini pasti catatan yang ditulis oleh orang ini.

Saya terus membaca buku itu. Tidak ada catatan. Dan saya berpikir bahwa saya tidak lagi dapat menemukan apa pun. Tetapi kemudian, di halaman 231, saya menemukan bookmark perusahaan - dengan teks tercetak:



Akankah saya akhirnya menemukan yang lain? Saya terus membaca buku itu. Kemudian, di akhir buku, di halaman 259, di bagian tentang teori relativistik elektron, saya menemukan yang berikut:



Saya membuka lipatan kertas ini:



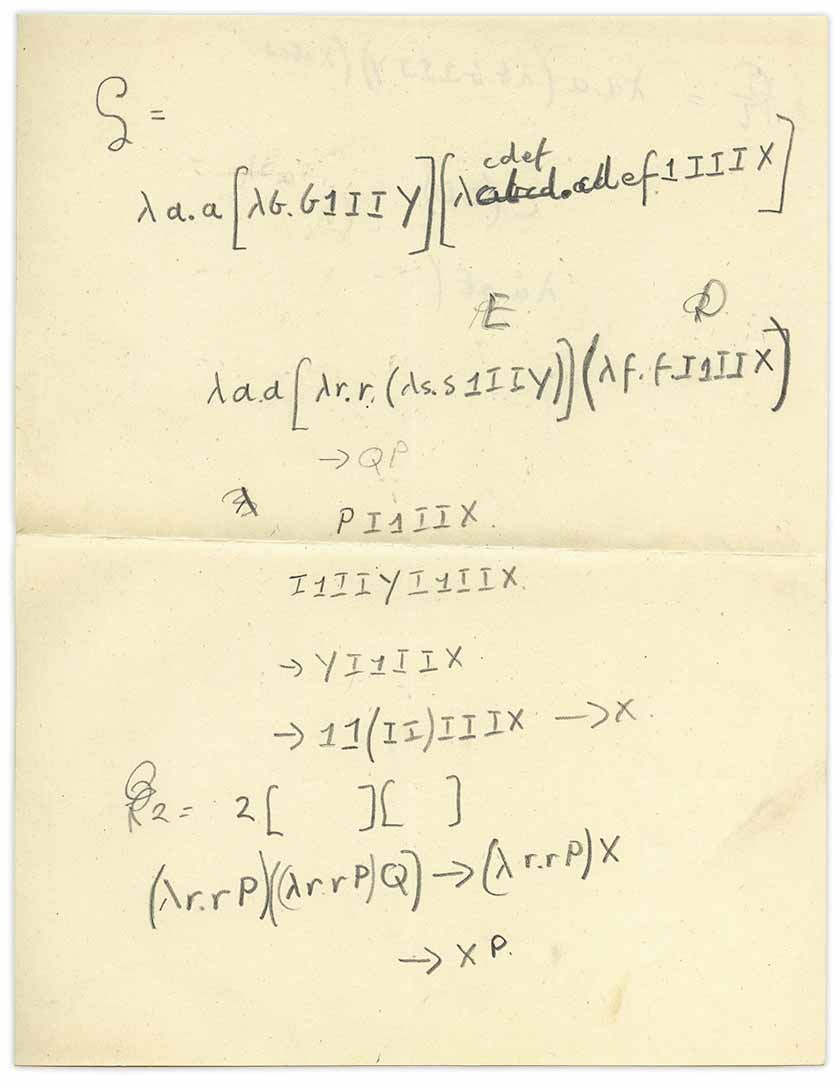
Saya segera menyadari bahwa ini adalah kalkulus lambda dengan campuran kombinator , tetapi bagaimana lembar ini muncul di sini? Ingatlah bahwa buku ini adalah buku tentang mekanika kuantum, tetapi lembar terlampir membahas logika matematika, atau yang sekarang disebut teori komputasi. Ini adalah tipikal dari tulisan Turing. Saya bertanya-tanya apakah Turing secara pribadi menulis catatan ini.

Bahkan saat sarapan, saya mencari di internet untuk sampel tulisan tangan Turing, tetapi tidak menemukan contoh dalam bentuk perhitungan, jadi saya tidak bisa menarik kesimpulan tentang identitas yang tepat dari tulisan tangan itu. Dan segera saya harus pergi. Dengan hati-hati aku mengemas buku itu, siap mengungkapkan rahasia halaman itu dan siapa yang menulisnya, dan membawanya bersamaku.

Tentang buku itu

Pertama-tama, mari kita bahas buku itu sendiri. Prinsip - prinsip Mekanika Kuantum oleh Paul Dirac diterbitkan dalam bahasa Inggris pada tahun 1930 dan segera diterjemahkan ke dalam bahasa Jerman. (Pendahuluan Dirac bertanggal 29 Mei 1930; itu milik penerjemah, Werner Bloch , pada 15 Agustus 1930.) Buku itu menjadi tonggak sejarah dalam pengembangan mekanika kuantum, secara sistematis membangun formalisme yang jelas untuk melakukan perhitungan, dan, antara lain, menjelaskan prediksi Dirac tentang positron , yang akan menjadi dibuka pada tahun 1932.

Mengapa Alan Turing memiliki buku dalam bahasa Jerman, bukan bahasa Inggris? Saya tidak tahu pasti ini, tetapi pada masa itu bahasa Jerman adalah bahasa utama sains, dan kita tahu bahwa Alan Turing bisa membacanya. (Setelah semua, dalam judul karya mesin Turing yang terkenal " Tentang angka yang dapat dihitung dengan lampiran untuk Masalah Penyelesaian (Entscheidungsproblem) ”adalah kata Jerman yang sangat panjang - dan di bagian utama artikel ia beroperasi dengan karakter Gothic yang agak tidak jelas dalam bentuk“ huruf Jerman ”, yang ia gunakan alih-alih, misalnya, karakter Yunani).

Alan Turing membeli buku itu sendiri atau menyerahkannya kepadanya? Saya tidak tahu. Di bagian dalam sampul buku Turing ada notasi pensil "20 / -", yang merupakan notasi standar "20 shilling", mirip dengan £ 1. Di halaman kanan ada tulisan "26.9.30" yang dihapus, konon artinya 26 September 1930 - mungkin tanggal buku itu pertama kali dibeli. Kemudian, di sudut paling kanan, nomor yang dihapus adalah "20". Mungkin ini lagi harganya. (Mungkinkah ini harga di Reichsmark , jika kita menganggap bahwa buku itu dijual di Jerman? Pada saat itu, 1 Reichsmark bernilai sekitar 1 shilling, harga Jerman mungkin akan ditulis seperti, misalnya, "20 RM".) Akhirnya, pada bagian dalam sampul belakang adalah "c 5 / -" - mungkin itu (dengan diskon besar) harga untuk buku bekas.

Mari kita lihat tanggal-tanggal utama kehidupan Alan Turing. Alan Turing dilahirkan pada 23 Juni 1912 (kebetulan, tepatnya 76 tahun sebelum Mathematica 1.0 ). Pada musim gugur 1931, ia memasuki King's College, Cambridge. Dia menerima gelar sarjana setelah studi tiga tahun standar, pada tahun 1934.

Pada 1920-an dan awal 1930-an, mekanika kuantum adalah topik hangat, dan Alan Turing tentu tertarik padanya. Kita tahu dari arsipnya bahwa pada tahun 1932, segera setelah buku itu diterbitkan, ia menerima " Yayasan Matematika Mekanika Kuantum " oleh John von Neumann (dalam bahasa Jerman ). Kita juga tahu bahwa pada tahun 1935 Turing menerima tugas dari fisikawan Cambridge Ralph Fowler tentang masalah studi mekanika kuantum. (Fowler mengusulkan menghitung konstanta dielektrik air , yang sebenarnya merupakan tugas yang sangat sulit, membutuhkan analisis penuh dengan teori medan kuantum yang berinteraksi, yang masih belum sepenuhnya diselesaikan).

Namun, kapan dan bagaimana Turing mendapatkan bukunya buku Dirac? Mengingat bahwa buku itu memiliki harga yang rusak, Turing diduga membelinya sudah digunakan. Siapa pemilik pertama buku itu? Catatan dalam buku ini tampaknya terutama berkaitan dengan struktur logis, perlu dicatat bahwa beberapa hubungan logis harus dianggap sebagai aksioma. Lalu bagaimana dengan catatan yang dilampirkan di halaman 127?

Yah, ini mungkin kebetulan, tetapi hanya di halaman 127 - Dirac berbicara tentang prinsip kuantum tindakan terkecil dan meletakkan dasar untuk integral di sepanjang jalur Feynman - yang merupakan dasar dari semua formalisme kuantum modern. Apa isi catatan itu? Ini berisi perpanjangan persamaan 14, yang merupakan persamaan untuk evolusi temporal dari amplitudo kuantum. Penulis catatan itu menggantikan Dirac A untuk amplitudo dengan ρ, mungkin mencerminkan catatan Jerman Jerman sebelumnya (analogi densitas cair). Kemudian penulis mencoba untuk memperluas aksi dalam kekuatan ℏ ( konstanta Planck dibagi 2π, yang kadang-kadang disebut konstanta Dirac ).

Tapi sepertinya dari apa yang terkandung di halaman, ada sedikit yang bisa dipelajari bermanfaat. Jika Anda menyimpan halaman dalam cahaya, itu berisi kejutan kecil - tanda air dengan tulisan "Z f. Physik. Chem B ”:



Ini adalah versi singkat Zeitschrift für physikalische Chemie, Abteilung B , jurnal kimia fisik Jerman, yang telah diterbitkan sejak 1928. Mungkin catatan itu ditulis oleh editor jurnal? Inilah judul majalah untuk tahun 1933. Mudahnya, editor terdaftar dengan lokasi mereka, dan salah satunya menonjol: "Born · Cambridge".



Ini adalah Max Bourne yang merupakan penulis aturan Bourne dan banyak lagi dalam teori mekanika kuantum (serta kakek dari penyanyi Olivia Newton-John ). Jadi, catatan ini mungkin ditulis oleh Max Born? Tapi, sayangnya, tidak demikian, karena tulisan tangan tidak cocok.

Bagaimana dengan bookmark di halaman 231? Ini dia dari dua sisi:



Bookmark itu aneh dan sangat cantik. Tapi kapan itu dibuat? Ada toko buku Heffers di Cambridge , meskipun sekarang menjadi bagian dari Blackwell. Selama lebih dari 70 tahun (hingga 1970), Heffers terletak di alamat, seperti yang ditunjukkan oleh bookmark, 3 dan 4 oleh Petty Cury .

Tab ini berisi kunci penting - ini adalah nomor telepon "Tel. 862. " Ternyata pada tahun 1939 sebagian besar Cambridge (termasuk Heffers) beralih ke nomor empat digit, dan, tentu saja, pada tahun 1940 bookmark dicetak dengan nomor telepon "modern". (Nomor telepon Inggris berangsur-angsur tumbuh lebih lama; ketika saya dibesarkan di Inggris pada 1960-an, nomor telepon kami adalah Oxford 56186 dan Kidmore End 2378. Sebagian, saya ingat angka-angka ini karena, anehnya, sekarang tidak terlihat, saya selalu memanggil nomor saya ketika menjawab panggilan masuk).

Penanda dalam formulir ini dicetak hingga 1939. Tapi berapa lama sebelum itu? Anda dapat menemukan beberapa pemindaian iklan Heffers lama di Internet, setidaknya sejak 1912 (bersama dengan "Kami meminta Anda untuk memenuhi permintaan Anda ...") mereka menambahkan "Telepon 862", menambahkan "(2 baris)". Ada juga beberapa penanda buku dengan desain serupa yang dapat ditemukan di buku-buku sejak tahun 1904 (walaupun tidak jelas apakah mereka asli untuk buku-buku ini (yaitu, dicetak pada saat yang sama) .Untuk keperluan penyelidikan kami, tampaknya kami dapat menyimpulkan bahwa buku ini berasal dari toko Heffers (yang, kebetulan, adalah toko buku utama di Cambridge) antara tahun 1930 dan 1939.

Halaman dengan kalkulus lambda

Jadi sekarang kita tahu sesuatu tentang kapan buku itu dibeli. Tapi bagaimana dengan "halaman kalkulus lambda"? Kapan ini ditulis? , - . , , 1932 1935 . ( , λ).

-. 1935 «» , . ( Comptes rendus ), ; , , , , .

1936 , - , . , 1934 , , , 1922 .
, - , ( - ). ( ) , , . 1936 ( ) « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

?

Jadi, mari kita melihat lebih dekat apa yang ada di kedua sisi daun. Mari kita mulai dengan lambda.

Berikut adalah cara untuk mendefinisikan fungsi "murni" atau "anonim" , dan mereka adalah konsep dasar dalam logika matematika, dan sekarang dalam pemrograman fungsional. Fungsi-fungsi ini cukup umum di Bahasa Wolfram , dan tugas mereka cukup mudah untuk dijelaskan. Sebagai contoh, seseorang menulis f [ x ] untuk menunjukkan fungsi f yang diterapkan pada argumen x. Dan ada banyak fungsi bernama f seperti Abs atau Sin atau Blur . Tetapi bagaimana jika seseorang ingin f [ x ] menjadi 2x +1 ? Tidak ada nama langsung untuk fungsi ini. Tetapi apakah ada bentuk penugasan lain, f [ x ]?

Jawabannya adalah ya: alih-alih kita menulis Function[a,2a+1] . Dan dalam bahasa Function [a,2a+1][x] Wolfram Function [a,2a+1][x] berlaku untuk argumen x, menghasilkan 2x+1 sebagai hasilnya. Function[a,2a+1] adalah fungsi "murni" atau "anonim", yang merupakan operasi murni untuk mengalikan dengan 2 dan menambahkan 1.

Jadi, λ dalam kalkulus lambda adalah analog yang tepat dari Fungsi dalam Bahasa Wolfram - dan karena itu, misalnya, λ a (2 a +1) setara dengan Function[a, 2a + 1] . (Perlu dicatat bahwa fungsi, katakanlah, Function[b,2b+1] setara; "variabel terkait" a atau b hanya tempat untuk menggantikan argumen fungsi - dan dalam Bahasa Wolfram mereka dapat dihindari dengan menggunakan opsi alternatif untuk mendefinisikan fungsi murni (2# +1)& ).

Dalam matematika tradisional, fungsi biasanya dianggap sebagai objek yang menampilkan data input (misalnya, bilangan bulat) dan data keluaran (yang juga, misalnya, bilangan bulat). Tapi apa objek Fungsi ini (atau λ)? Intinya, ini adalah operator struktural yang mengambil ekspresi dan mengubahnya menjadi fungsi. Ini mungkin tampak sedikit aneh dalam hal matematika tradisional dan bentuk penulisan matematika, tetapi jika seseorang perlu memanipulasi karakter sewenang-wenang, yang jauh lebih alami, bahkan jika pada awalnya tampaknya agak abstrak. (Perlu dicatat bahwa ketika pengguna mempelajari Bahasa Wolfram, saya selalu bisa mengatakan bahwa mereka telah mengatasi ambang batas pemikiran abstrak ketika mereka mendapatkan ide Fungsi ).

Lambdas hanyalah bagian dari apa yang ada di halaman. Ada konsep lain yang bahkan lebih abstrak - ini adalah kombinator . Pertimbangkan baris PI1IIx agak tidak jelas? Apa artinya itu? Sebenarnya, ini adalah urutan kombinator, atau, beberapa komposisi abstrak fungsi simbolik.

Superposisi fungsi yang biasa, cukup akrab dalam matematika, dalam Bahasa Wolfram dapat ditulis dalam bentuk: f[g[x]] - yang berarti "menerapkan f pada hasil penerapan g ke x ". Tetapi apakah kurung benar-benar diperlukan untuk ini? Dalam Wolfram, f@g@ x adalah bentuk notasi alternatif. Dalam posting ini, kami bergantung pada definisi Bahasa Wolfram: operator @ dikaitkan dengan sisi kanan, sehingga f@g@x setara dengan f@(g@x) .

Tapi apa artinya entri (f@g)@x ? Ini sama dengan f[g][x] . Dan jika f dan g adalah fungsi biasa dalam matematika, itu tidak ada gunanya, tetapi jika f adalah fungsi tingkat tinggi , maka f[g] itu sendiri bisa menjadi fungsi yang bisa diterapkan ke x .

Catatan di sini masih ada beberapa kerumitan. Dalam f[] - f adalah fungsi dari satu argumen. Dan f[] sama dengan menulis Function[a, f[a]][x] . Tetapi bagaimana dengan fungsi dua argumen, katakanlah, f[x,y] ? Ini dapat ditulis sebagai Function[{a,b},f[a, b]][x, y] . Tetapi bagaimana dengan Function[{a},f[a,b]] ? Apa ini Ada "variabel bebas" b , yang hanya diteruskan ke fungsi. Function[{b},Function[{a},f[a,b]]] akan mengikat variabel ini, dan kemudian Function[{b},Function[{a},f [a, b]]][y][x] memberikan f[x,y] lagi. (Pengaturan fungsi sehingga memiliki satu argumen disebut "currying" untuk menghormati ahli logika ilmuwan bernama Haskell Curry ).

Jika variabel bebas ada, yaitu, ada banyak kesulitan yang berbeda mengenai bagaimana fungsi dapat didefinisikan, tetapi jika kita membatasi diri kita pada Fungsi atau objek λ yang tidak memiliki variabel bebas, maka pada dasarnya mereka dapat diatur secara bebas. Objek semacam itu disebut kombinator.

Combinators memiliki sejarah panjang. Diketahui bahwa mereka pertama kali diusulkan pada tahun 1920 oleh murid David Gilbert , Moses Schoenfinkel .

Pada waktu itu, baru-baru ini diketahui bahwa tidak perlu menggunakan ekspresi Dan , Atau dan Tidak untuk mewakili ekspresi dalam logika proposisional standar: cukup menggunakan satu-satunya operator, yang sekarang kita sebut Nand (karena, misalnya, jika kita menulis Nand sebagai ·, Kemudian Or[a,b] mengambil bentuk (a · a) · (b · b) ). Schönfinkel ingin menemukan representasi minimal yang sama dari logika predikat, atau pada dasarnya logika, termasuk fungsi.

Dia datang dengan dua "kombinator" S dan K. Dalam Bahasa Wolfram, ini ditulis sebagai
K [x _] [y_] → x dan S [x _] [y _] [z_] → x [z] [y [z]].

Perlu dicatat bahwa dimungkinkan untuk menggunakan kedua kombinator ini untuk melakukan perhitungan apa pun. Jadi misalnya

S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]

dapat digunakan sebagai fungsi untuk menambahkan dua bilangan bulat.

Semua ini, secara sederhana, adalah objek yang agak abstrak, tetapi sekarang setelah kita memahami apa itu mesin Turing dan kalkulus lambda, kita dapat melihat bahwa kombinator Schoenfinkel sebenarnya mengantisipasi konsep komputasi universal. (Dan yang lebih luar biasa lagi, definisi S dan K tahun 1920 minimal sederhana, dan menyerupai mesin Turing universal yang sangat sederhana yang saya usulkan pada 1990-an, yang universalitasnya terbukti pada 2007 ).

Tetapi kembali ke selebaran dan baris kami PI1IIx . Karakter yang direkam di sini adalah kombinator, dan mereka semua dirancang untuk mendefinisikan suatu fungsi. Di sini definisinya adalah bahwa superposisi fungsi harus kiri-asosiatif, jadi fgx tidak boleh diartikan sebagai f @ g @ x atau f @ (g @ x) atau f [g [x]], melainkan sebagai (f @ g) ) @x atau f [g] [x]. Kami akan menerjemahkan entri ini ke dalam format yang nyaman untuk digunakan oleh Bahasa Wolfram: PI1IIx akan mengambil bentuk p [i] [satu] [i] [i] [x] .

Kenapa menulis sesuatu seperti itu? Untuk menjelaskan ini, kita perlu membahas konsep angka Gereja (dinamai Gereja Alonzo). Katakanlah kita hanya bekerja dengan simbol dan dengan lambdas atau kombinator Apakah ada cara untuk menggunakannya untuk menentukan bilangan bulat?

Bagaimana kalau mengatakan bahwa angka n sesuai dengan Function[x, Nest[f,x,n]] ? Atau, dengan kata lain, itu (dalam notasi lebih pendek):

1 adalah f[#]&
2 adalah f[f[#]]&
3 adalah f[f[f[#]]]& dan seterusnya.

Semua ini mungkin tampak agak lebih tidak jelas, tetapi alasan mengapa hal itu menarik adalah bahwa hal itu memungkinkan kita untuk melakukan semuanya sepenuhnya simbolis dan abstrak, tanpa harus secara eksplisit berbicara tentang sesuatu seperti bilangan bulat.

Dengan metode menentukan angka, bayangkan, misalnya, menambahkan dua angka: 3 dapat direpresentasikan sebagai f[f[f[#]]]& dan 2 adalah f[f[#]]& . Anda dapat menambahkannya hanya dengan menerapkan salah satu di antaranya:



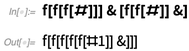
Tapi seperti apa f ? Itu bisa apa saja! Dalam arti tertentu, "pergi ke lambda" ke akhir dan mewakili angka menggunakan fungsi yang mengambil f sebagai argumen. Dengan kata lain, bayangkan 3, misalnya, sebagai Function[f,f[f[f[#]]] &] atau Function[f,Function[x,f[f[f[x]]]] . (kapan dan bagaimana Anda perlu menamai variabel adalah tangkapan dalam kalkulus lambda).

Pertimbangkan sebuah fragmen dari karya Turing 1937, Computability dan λ-Diffusibility , yang mengatur objek persis seperti yang baru saja kita bahas:



Di sini, rekaman mungkin agak membingungkan. Turing's x adalah f kita, dan x'nya (komposer melakukan kesalahan dengan memasukkan spasi) adalah x kita. Tapi di sini pendekatan yang sama persis digunakan.

Jadi, mari kita lihat garis segera setelah lipatan di depan daun. Ini adalah I1IIYI1IIx . Menurut bentuk Bahasa Wolfram, ini adalah i[one][i][i][y][i][one][i][i][x] . Tapi di sini saya adalah fungsi yang identik, oleh karena itu i[one] hanya mengembalikan satu . Sementara itu, satu adalah representasi numerik Gereja untuk 1 atau Function[f,f[#]&] . Tetapi dengan definisi ini, one[] menjadi a[#]& dan one[a][b] menjadi a[b] . (Omong-omong, i[][b] , atau Identity[][b] juga merupakan [b] ).

Akan jauh lebih jelas jika kita menuliskan aturan penggantian untuk i dan satu , daripada langsung menggunakan kalkulus lambda. Hasilnya akan sama. Terapkan aturan ini secara eksplisit, kami mendapatkan:



Dan ini persis sama dengan yang disajikan pada catatan singkat pertama:



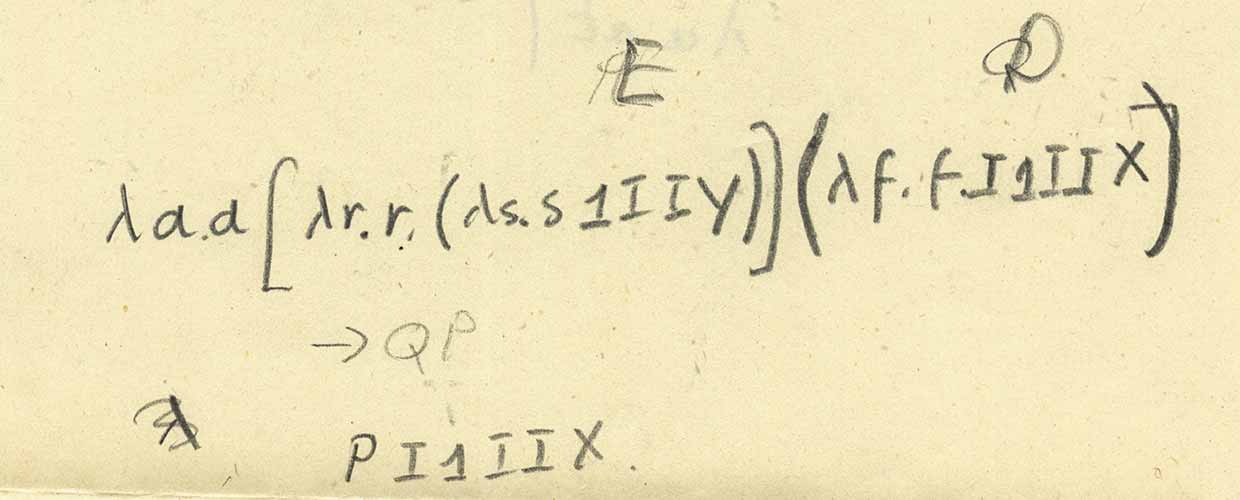
Sekarang mari kita lihat daun lagi, di atasnya:



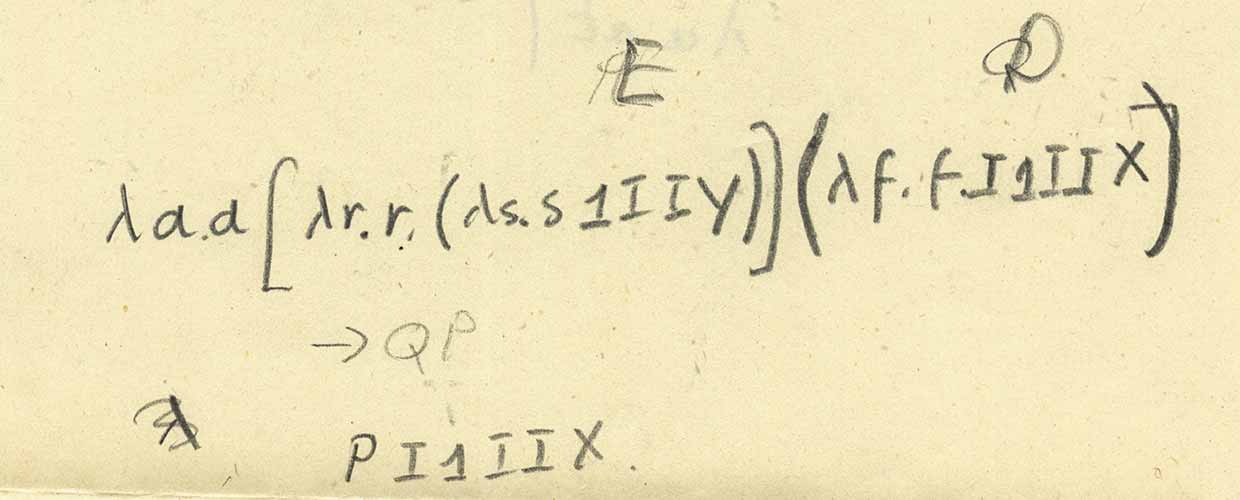
Ada objek yang agak membingungkan dan tidak dapat dipahami "E" dan "D", tetapi yang mereka maksudkan adalah "P" dan "Q", sehingga kita dapat menulis ekspresi dan menghitungnya (perhatikan bahwa di sini - setelah beberapa kebingungan dengan yang terakhir simbol - "ilmuwan misterius" menempatkan [...] dan (...) untuk mewakili fungsi aplikasi):



Jadi ini adalah singkatan pertama yang ditampilkan. Untuk melihat lebih banyak, mari gantikan definisi untuk Q:



Kami mendapatkan persis singkatan berikut yang ditampilkan. Apa yang terjadi jika kita mengganti ekspresi untuk P?



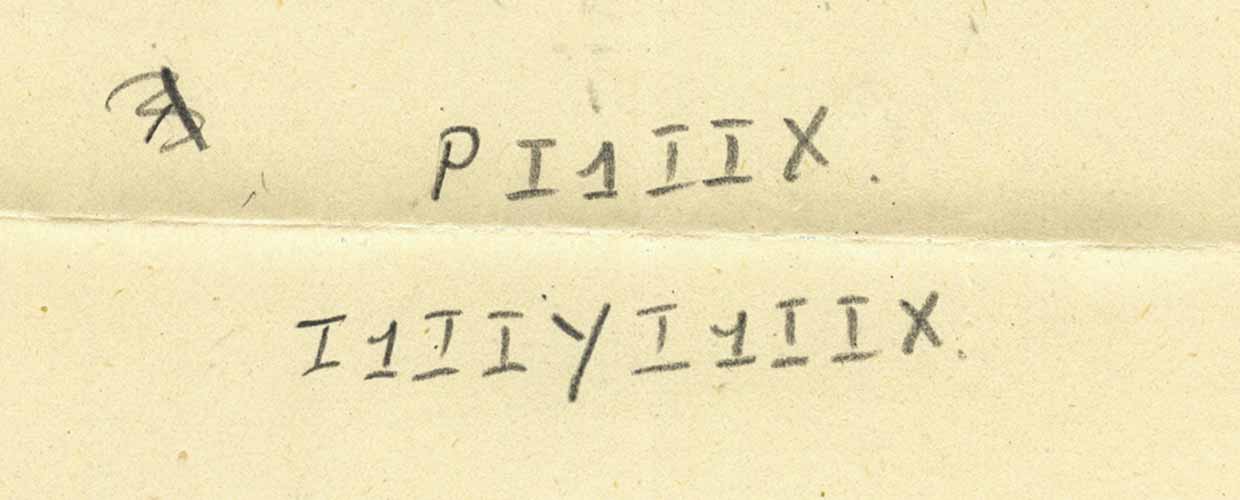
Inilah hasilnya:



Dan sekarang, menggunakan fakta bahwa saya adalah fungsi yang menghasilkan argumen itu sendiri, kita mendapatkan:



Aduh! Tapi ini bukan baris rekaman berikutnya. Apakah ada kesalahan di sini? Tidak jelas. Karena, pada akhirnya, tidak seperti kebanyakan kasus lain, tidak ada panah yang menunjukkan bahwa baris berikutnya mengikuti dari yang sebelumnya.

Ini semacam misteri, tapi mari kita lanjutkan ke bagian bawah selebaran:



Di sini 2 adalah nomor Gereja, yang didefinisikan, misalnya, dengan pola two[a_] [b_] → a[a[b]] . Perhatikan bahwa ini sebenarnya bentuk baris kedua jika a diperlakukan sebagai Function[r,r[]] dan b sebagai q . Jadi, kami berharap hasil perhitungannya adalah sebagai berikut:



Namun demikian, ungkapan [b] terletak di dalam dapat ditulis sebagai x (mungkin berbeda dari x yang sebelumnya ditulis pada lembar) - sebagai hasilnya, kita mendapatkan hasil akhir:



Jadi, kita dapat menguraikan sedikit dari apa yang terjadi pada daun ini, tetapi setidaknya satu teka-teki yang masih tersisa adalah apa yang seharusnya menjadi Y.

Faktanya, logika kombinatorial memiliki kombinator-Y standar: kombinator titik-tetap . Secara formal, ini didefinisikan oleh fakta bahwa Y [ f ] harus sama dengan f [Y [ f ]], atau, dengan kata lain, Y [ f ] tidak berubah ketika f diterapkan, jadi ini adalah titik tetap untuk f . (Combinator Y dikaitkan dengan # 0 dalam Bahasa Wolfram.)

Saat ini, Y-combinator telah menjadi terkenal berkat akselerator peluncuran Y-Combinator , yang disebut Paul Graham (yang sejak lama adalah penggemar pemrograman fungsional dan bahasa pemrograman LISP dan mengimplementasikan toko web pertama berdasarkan bahasa ini). Dia pernah mengatakan kepada saya secara pribadi, " tidak ada yang mengerti apa yang Y adalah kombinator ." (Perlu dicatat bahwa Y Combinator adalah tepat yang memungkinkan perusahaan untuk menghindari operasi titik tetap ...)

Combinator Y (seperti combinator titik tetap) ditemukan beberapa kali. Turing benar-benar muncul dengan implementasinya pada tahun 1937, yang ia sebut Θ. Tetapi apakah huruf "Y" di halaman kami adalah kombinator titik tetap yang terkenal? Mungkin juga tidak. Jadi apa "Y" kita? Pertimbangkan pengurangan ini:



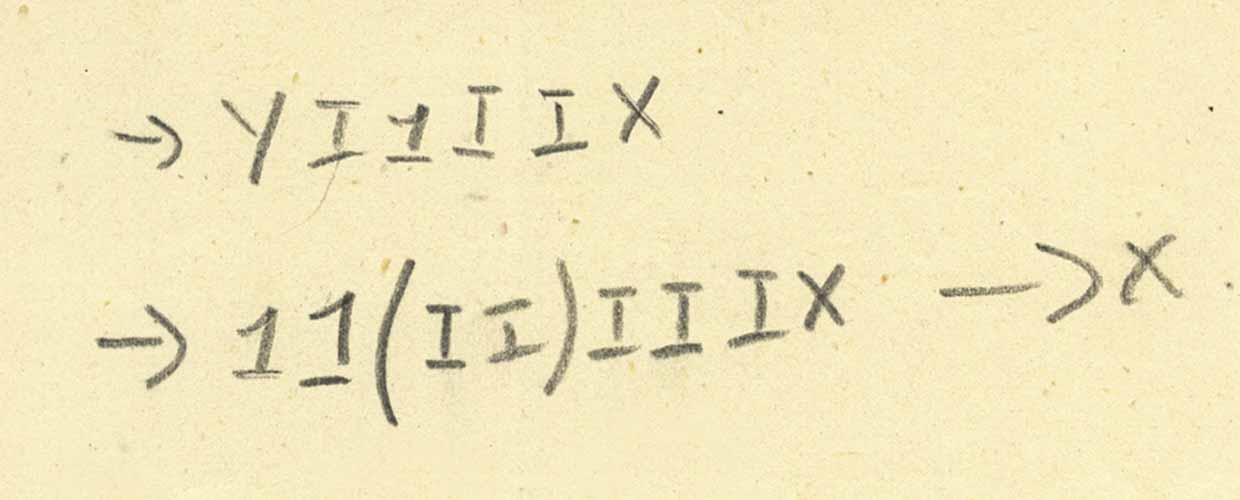
Tetapi informasi ini jelas tidak cukup untuk menentukan dengan jelas apa itu Y. Jelas bahwa Y beroperasi tidak hanya dengan satu argumen; tampaknya masalahnya setidaknya adalah dua argumen, tetapi tidak jelas (setidaknya bagi saya) berapa banyak argumen yang diperlukan untuk input dan apa yang dilakukannya.

Akhirnya, walaupun kita dapat memahami banyak bagian selebaran, kita harus mengatakan bahwa dalam skala global tidak jelas apa yang dilakukan pada selebaran itu. Meskipun membutuhkan banyak penjelasan tentang apa yang disajikan pada lembar, itu cukup mendasar dalam kalkulus lambda dan menggunakan kombinator.

Agaknya, ini adalah upaya untuk membuat "program" sederhana - menggunakan kalkulus lambda dan kombinator untuk melakukan sesuatu. Tetapi sejauh ini tipikal untuk rekayasa terbalik, sulit bagi kita untuk mengatakan apa "sesuatu" ini dan apa tujuan umum "yang bisa dijelaskan".

Ada fitur lain yang disajikan pada lembar, yang layak dikomentari di sini - adalah penggunaan berbagai jenis kurung. Dalam matematika tradisional, tanda kurung terutama digunakan untuk semuanya - dan aplikasi fungsi (seperti dalam f (x) ), dan pengelompokan anggota (seperti dalam (1 + x) (1-x) , atau, kurang jelas, a (1- x) ). (Dalam Bahasa Wolfram, kami memisahkan berbagai penggunaan tanda kurung - dalam tanda kurung siku untuk mendefinisikan f [x] - dan tanda kurung hanya digunakan untuk pengelompokan).

Ketika kalkulus lambda pertama kali muncul, ada banyak pertanyaan tentang penggunaan tanda kurung. Kemudian, Alan Turing menulis seluruh karya (tidak diterbitkan) berjudul " Mengubah bentuk matematika notasi dan fraseologi ", tetapi sudah pada tahun 1937 ia merasa bahwa ia perlu menggambarkan definisi modern (bukan hacker) untuk kalkulus lambda (yang, omong-omong, muncul dari untuk Gereja).

Dia mengatakan bahwa f yang diterapkan ke g harus ditulis {f} (g) , kecuali f adalah satu-satunya karakter, dalam hal ini bisa menjadi f (g) . Dia kemudian mengatakan bahwa lambda (seperti dalam Function[a, b] ) harus ditulis sebagai λ a [ b ] atau, sebagai alternatif, λ a . b .

Namun, mungkin pada tahun 1940 seluruh gagasan untuk menggunakan {...} dan [...] untuk menunjukkan objek yang berbeda dibuang, terutama yang mendukung tanda kurung dengan gaya matematika standar.

Lihatlah bagian atas halaman:



Dalam bentuk ini, sulit dipahami. Dalam definisi Gereja, tanda kurung siku adalah untuk pengelompokan, dengan braket pembuka yang menggantikan suatu periode. Dengan menggunakan definisi ini, menjadi jelas bahwa Q (akhirnya diberi label sebagai D), terlampir dalam tanda kurung pada akhirnya, adalah apa yang berlaku untuk seluruh lambda awal.

Bahkan, tanda kurung siku di sini tidak membatasi tubuh lambda; sebagai gantinya, itu sebenarnya mewakili aplikasi lain dari fungsi, dan tidak ada indikasi eksplisit di mana tubuh lambda berakhir. Pada akhirnya, dapat dilihat bahwa "ilmuwan misterius" mengubah braket kuadrat penutup menjadi satu lingkaran, dengan demikian secara efektif menerapkan definisi Gereja - dan memaksanya untuk menghitung ekspresi, seperti yang ditunjukkan pada lembar.

Jadi, apa arti potongan kecil ini? Saya pikir ini menunjukkan bahwa halaman itu ditulis pada 1930-an, atau tidak terlalu lama setelah itu, karena legenda untuk kurung belum menetap.

Jadi tulisan tangan siapa itu?

Jadi, sebelum itu kita berbicara tentang apa yang tertulis di halaman. Tetapi bagaimana dengan orang yang menulisnya sama saja?

Kandidat yang paling jelas untuk peran ini adalah Alan Turing sendiri, karena, bagaimanapun juga, halaman itu ada di dalam bukunya. Dalam hal konten, tampaknya tidak ada yang tidak sesuai dengan fakta bahwa Alan Turing dapat menulis ini - bahkan pada saat ia pertama kali berurusan dengan kalkulus lambda setelah ia menerima artikel Gereja pada awal 1936.

Bagaimana dengan tulisan tangan? Apakah itu milik Alan Turing? Pertimbangkan beberapa sampel yang masih hidup, yang, seperti yang kita ketahui dengan pasti, ditulis oleh Alan Turing:



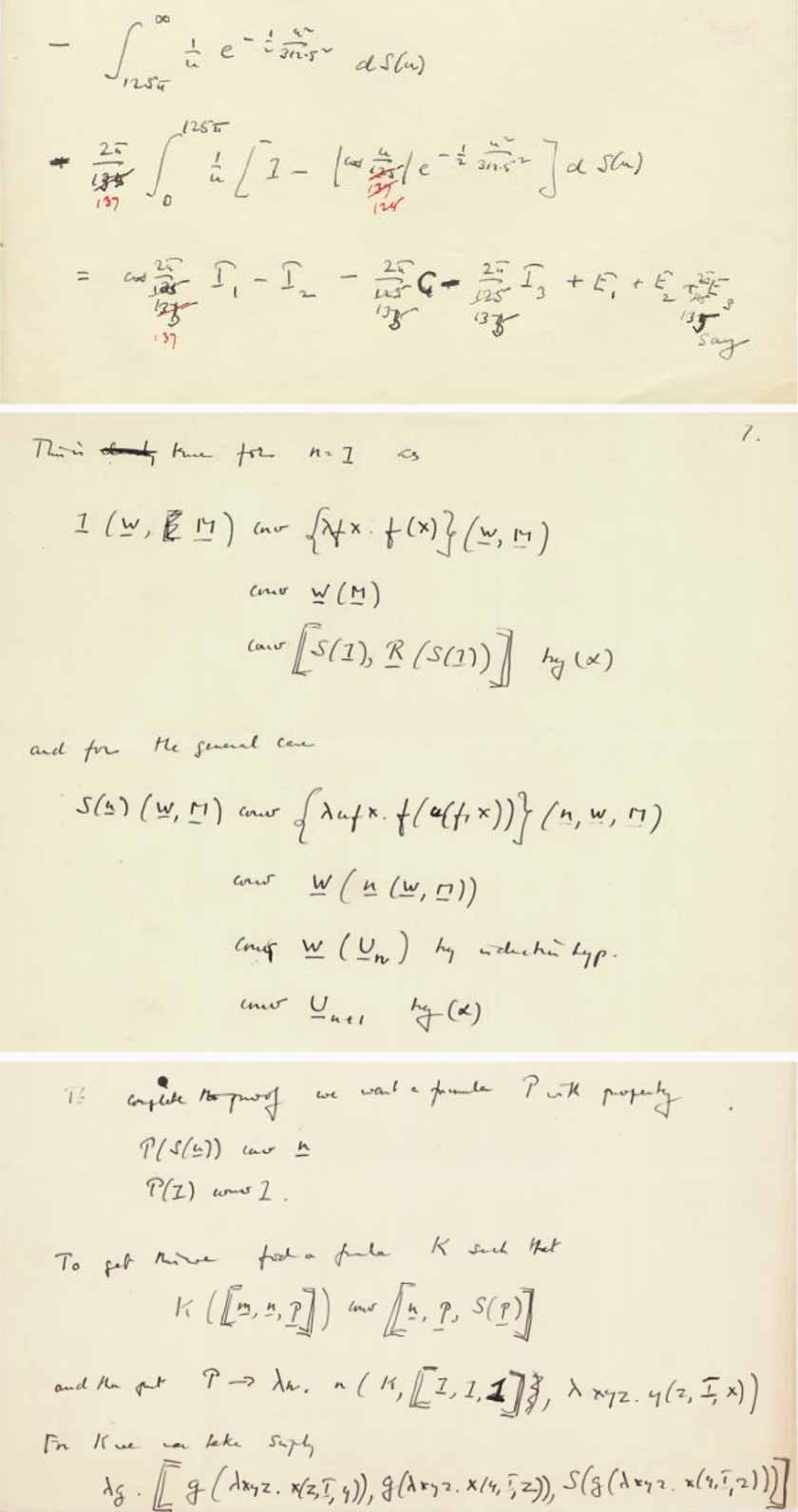
Teks yang disajikan jelas terlihat sangat berbeda, tetapi bagaimana dengan notasi yang digunakan dalam teks? Paling tidak, menurut pendapat saya, ini tidak terlihat begitu jelas - dan dapat diasumsikan bahwa perbedaan dapat disebabkan oleh fakta bahwa sampel yang ada (disajikan dalam arsip) ditulis, sehingga dapat dikatakan, "di akhir", sementara kami sebuah halaman adalah cerminan dari karya pemikiran.

Ternyata menjadi nyaman untuk penyelidikan kami bahwa ada halaman di arsip Turing di mana ia menulis daftar karakter yang diperlukan untuk notasi. Dan ketika membandingkan karakter-karakter ini huruf demi huruf, mereka terlihat sangat mirip dengan saya (catatan-catatan ini dibuat selama masa Turing ketika dia mempelajari pertumbuhan tanaman , maka muncul notasi “area daun”):



Saya ingin menyelidiki ini lebih dalam, jadi saya mengirim sampel ke Sheila Lowe , seorang ahli tulisan tangan profesional (dan penulis tulisan tangan), yang pernah saya temui - hanya menyajikan selebaran kami sebagai "sampel A" dan tulisan tangan Turing yang ada sebagai "Contoh" B ". Jawabannya final dan negatif: “ Gaya penulisan sama sekali berbeda. Adapun kepribadian, penulis sampel "B" memiliki cara berpikir yang lebih cepat dan lebih intuitif daripada penulis sampel "A ". "

Saya belum sepenuhnya yakin akan hal ini, tetapi memutuskan bahwa sudah waktunya untuk mencari opsi lain.

Jadi jika ternyata Turing tidak menulis ini, lalu siapa yang melakukannya? Norman Rutledge mengatakan kepada saya bahwa dia menerima buku dari Robin Gandhi, yang adalah eksekutor Turing. Jadi saya mengirim "Sampel" C "" dari Gandhi:



Tetapi kesimpulan awal Sheila adalah bahwa tiga sampel itu mungkin ditulis oleh tiga orang yang berbeda, sekali lagi mencatat bahwa sampel "B" diperoleh dari " pemikir tercepat - orang yang kemungkinan besar paling rela mencari solusi yang tidak biasa untuk masalah " . (Saya merasa senang bahwa seorang spesialis tulisan tangan modern akan memberikan penilaian tulisan tangan Turing sedemikian, mengingat betapa aktifnya setiap orang dalam tugas sekolah Turing tahun 1920-an mengeluh tentang tulisan tangannya).

Nah, pada saat itu, tampaknya Turing dan Gandhi dikeluarkan dari daftar "tersangka". Jadi siapa yang bisa menulis ini? Saya mulai memikirkan orang-orang yang bisa meminjamkan bukunya untuk Turing. Tentu saja, pada saat yang sama, mereka harus dapat melakukan perhitungan menggunakan kalkulus lambda.

Saya menyarankan agar orang itu dari Cambridge, atau setidaknya dari Inggris, diberi tanda air di atas kertas. Saya salah mengira hipotesis kerja bahwa 1936 atau lebih adalah waktu yang tepat untuk menulis ini. Jadi siapa yang dia kenal saat itu dan dengan siapa Turing berkomunikasi? . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
Pendaftaran untuk kursus baru . Kursus online siap.
Wolfram Language.