Memecahkan persamaan regresi linier sederhana

Artikel ini membahas beberapa metode untuk menentukan persamaan matematika dari garis regresi sederhana (berpasangan).

Semua metode untuk menyelesaikan persamaan yang dibahas di sini didasarkan pada metode kuadrat terkecil. Kami menunjukkan metode sebagai berikut:

• Solusi analitik
• Keturunan gradien
• Penurunan gradien stokastik

Untuk setiap metode untuk menyelesaikan persamaan garis lurus, artikel ini menjelaskan berbagai fungsi yang terutama dibagi menjadi yang ditulis tanpa menggunakan perpustakaan NumPy dan yang menggunakan NumPy untuk perhitungan. Penggunaan NumPy yang terampil diyakini mengurangi biaya komputasi.

Semua kode dalam artikel ini ditulis dalam python 2.7 menggunakan Notebook Jupyter . Kode sumber dan contoh file data yang diposting di github

Artikel ini lebih fokus pada pemula dan mereka yang sudah sedikit demi sedikit mulai menguasai studi bagian yang sangat luas dalam kecerdasan buatan - pembelajaran mesin.

Untuk menggambarkan materi, kami menggunakan contoh yang sangat sederhana.

Contoh kondisi

Kami memiliki lima nilai yang mencirikan ketergantungan Y pada X (Tabel No. 1):

Tabel No. 1 "Ketentuan contoh"



Kami menganggap bahwa nilai-nilai $$$x_i$ Apakah bulan dalam setahun, dan $$$y_i$ - Pendapatan bulan ini. Dengan kata lain, pendapatan tergantung pada bulan dalam setahun, dan $$$x_i$ - satu-satunya tanda yang bergantung pada pendapatan.

Contohnya adalah begitu-begitu, baik dalam hal ketergantungan pendapatan bersyarat pada bulan tahun, dan dalam hal jumlah nilai - ada sangat sedikit dari mereka. Namun, penyederhanaan ini akan memungkinkan apa yang disebut dengan jari untuk menjelaskan, tidak selalu dengan mudah, materi yang diserap oleh pemula. Dan juga kesederhanaan angka akan memungkinkan, tanpa biaya tenaga kerja yang signifikan, mereka yang ingin menyelesaikan contoh di atas kertas.

Misalkan ketergantungan yang diberikan dalam contoh dapat didekati dengan sangat baik oleh persamaan matematika dari garis regresi sederhana (berpasangan) dari bentuk:

$$

$$Y = a + bx$$

dimana $$$x$ - ini adalah bulan di mana pendapatan diterima, $$$Y$ - pendapatan sesuai dengan bulan, $$$a$ dan $$$b$ - koefisien regresi dari garis yang diperkirakan.

Perhatikan bahwa koefisien $$$b$ sering disebut kemiringan atau kemiringan garis estimasi; mewakili jumlah yang digunakan untuk mengubah $$$Y$ saat berubah $$$x$ .

Jelas, tugas kita dalam contoh ini adalah untuk memilih koefisien tersebut dalam persamaan $$$a$ dan $$$b$ di mana penyimpangan estimasi pendapatan bulanan kami dari jawaban yang benar, yaitu nilai-nilai yang disajikan dalam sampel akan minimal.

Metode kuadrat terkecil

Sesuai dengan metode kuadrat terkecil, penyimpangan harus dihitung dengan mengkuadratkannya. Teknik seperti itu menghindari saling pembayaran penyimpangan, jika mereka memiliki tanda-tanda yang berlawanan. Sebagai contoh, jika dalam satu kasus, deviasi adalah +5 (plus lima), dan di -5 lainnya (minus lima), maka jumlah deviasi akan saling dibayar dan akan menjadi 0 (nol). Anda tidak dapat menyia-nyiakan penyimpangan, tetapi gunakan properti modul dan kemudian semua penyimpangan akan menjadi positif dan akan menumpuk di dalam kita. Kami tidak akan membahas hal ini secara rinci, tetapi hanya menunjukkan bahwa untuk kenyamanan perhitungan, adalah kebiasaan untuk menyamakan penyimpangan.

Inilah tampilan rumus dengan bantuan yang kami tentukan jumlah terkecil dari penyimpangan kuadrat (kesalahan):

$$

$$ERR (x) = \ jumlah \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ jumlah \ limit_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rightarrow min$$

dimana $$$f (x_i) = a + bx_i$ Apakah fungsi perkiraan jawaban yang benar (yaitu, pendapatan yang dihitung oleh kami),

$$$y_i$ - ini adalah jawaban yang benar (pendapatan disediakan dalam sampel),

$$$i$ Adalah indeks sampel (jumlah bulan di mana penyimpangan ditentukan)

Kami membedakan fungsi, menentukan persamaan diferensial parsial, dan siap untuk melanjutkan ke solusi analitis. Tetapi pertama-tama, mari kita menyimpang singkat tentang apa itu diferensiasi dan mengingat makna geometris turunannya.

Diferensiasi

Diferensiasi adalah operasi menemukan turunan dari suatu fungsi.

Untuk apa turunannya? Turunan dari suatu fungsi mencirikan laju perubahan suatu fungsi dan menunjukkan arahnya. Jika turunan pada titik tertentu positif, maka fungsi meningkat, jika tidak, fungsi menurun. Dan semakin besar nilai modulo turunan, semakin tinggi tingkat perubahan nilai-nilai fungsi, serta semakin curam sudut grafik fungsi.

Sebagai contoh, dalam kondisi sistem koordinat Cartesian, nilai turunan pada titik M (0,0) sama dengan +25 berarti pada titik tertentu, ketika nilainya digeser $$$x$ hak untuk unit sewenang-wenang, nilai $$$y$ meningkat 25 unit konvensional. Pada grafik, terlihat seperti sudut ketinggian yang cukup curam $$$y$ dari titik tertentu.

Contoh lain. Nilai turunan dari -0.1 berarti bahwa ketika diimbangi $$$x$ per unit konvensional, nilai $$$y$ berkurang hanya 0,1 unit konvensional. Pada saat yang sama, pada grafik fungsi, kita dapat mengamati kemiringan yang hampir tidak terlihat. Menggambar analogi dengan gunung, kita tampaknya sangat lambat menuruni lereng lembut dari gunung, tidak seperti contoh sebelumnya, di mana kita harus mengambil puncak yang sangat curam :)

Jadi, setelah membedakan fungsinya $$$ERR (x) = \ jumlah \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ berdasarkan koefisien $$$a$ dan $$$b$ , kami mendefinisikan persamaan turunan parsial dari orde pertama. Setelah mendefinisikan persamaan, kita mendapatkan sistem dua persamaan, memutuskan mana kita dapat memilih nilai-nilai koefisien tersebut $$$a$ dan $$$b$ di mana nilai-nilai derivatif yang sesuai pada titik-titik tertentu berubah dengan nilai yang sangat, sangat kecil, dan dalam kasus solusi analitis mereka tidak berubah sama sekali. Dengan kata lain, fungsi kesalahan pada koefisien yang ditemukan mencapai minimum, karena nilai turunan parsial pada titik-titik ini adalah nol.

Jadi, menurut aturan diferensiasi, persamaan turunan parsial dari orde 1 berkenaan dengan koefisien $$$a$ akan berbentuk:

$$

$$2na + 2b \ jumlah \ limit_ {i = 1} ^ nx_i - 2 \ jumlah \ limit_ {i = 1} ^ ny_i = 2 (na + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i)$$

Persamaan derivatif urutan pertama sehubungan dengan $$$b$ akan berbentuk:

$$

$$2a \ jumlah \ limit_ {i = 1} ^ nx_i + 2b \ jumlah \ limit_ {i = 1} ^ nx ^ 2_i - 2 \ jumlah \ limit_ {i = 1} ^ nx_iy_i = 2 \ jumlah \ limit_ {i = 1} ^ nx_i (a + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i)$$

Akibatnya, kami mendapat sistem persamaan yang memiliki solusi analitik yang cukup sederhana:

\ mulai {persamaan *}
\ begin {cases}
na + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i = 0
\\
\ jumlah \ limit_ {i = 1} ^ nx_i (a + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {persamaan *}

Sebelum menyelesaikan persamaan, pra-muat, periksa pemuatan yang benar dan format data.

Unduh dan format data

Perlu dicatat bahwa karena fakta bahwa untuk solusi analitis, dan kemudian untuk gradien dan penurunan gradien stokastik, kita akan menggunakan kode dalam dua variasi: menggunakan perpustakaan NumPy dan tanpa menggunakannya, kita perlu memformat data sesuai (lihat kode).

Visualisasi

Sekarang, setelah kami, pertama, mengunduh data, kedua, kami memeriksa pemuatan yang benar dan akhirnya memformat data, kami akan melakukan visualisasi pertama. Seringkali, metode pairplot dari perpustakaan Seaborn digunakan untuk ini. Dalam contoh kami, karena jumlah yang terbatas, tidak masuk akal untuk menggunakan perpustakaan Seaborn . Kami akan menggunakan pustaka Matplotlib biasa dan hanya melihat scatterplot.


Jadwal No. 1 "Ketergantungan pendapatan pada bulan tahun ini"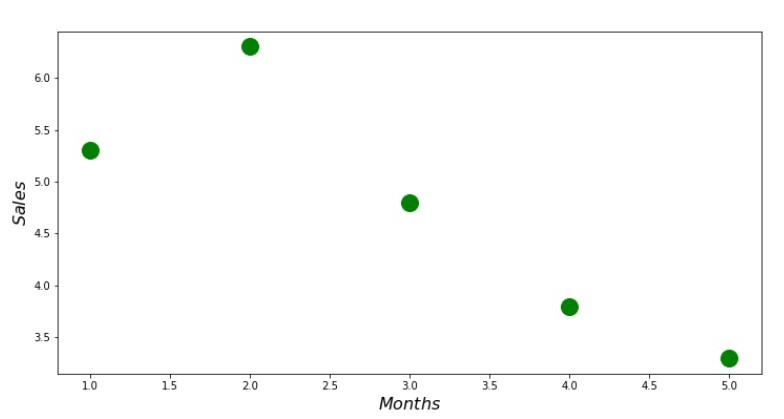

Solusi analitik

Kami akan menggunakan alat yang paling umum dalam python dan menyelesaikan sistem persamaan:

\ mulai {persamaan *}
\ begin {cases}
na + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i = 0
\\
\ jumlah \ limit_ {i = 1} ^ nx_i (a + b \ jumlah \ limit_ {i = 1} ^ nx_i - \ jumlah \ limit_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {persamaan *}

Menurut aturan Cramer, kami menemukan penentu bersama, serta penentu oleh $$$a$ dan oleh $$$b$ , setelah itu, membagi determinan dengan $$$a$ pada penentu umum - kami menemukan koefisien $$$a$ , sama halnya, temukan koefisien $$$b$ .


Inilah yang kami dapatkan:



Jadi, nilai-nilai koefisien ditemukan, jumlah penyimpangan kuadrat ditetapkan. Kami menggambar garis lurus pada histogram hamburan sesuai dengan koefisien yang ditemukan.


Jadwalkan No. 2 “Jawaban yang Benar dan Diperkirakan”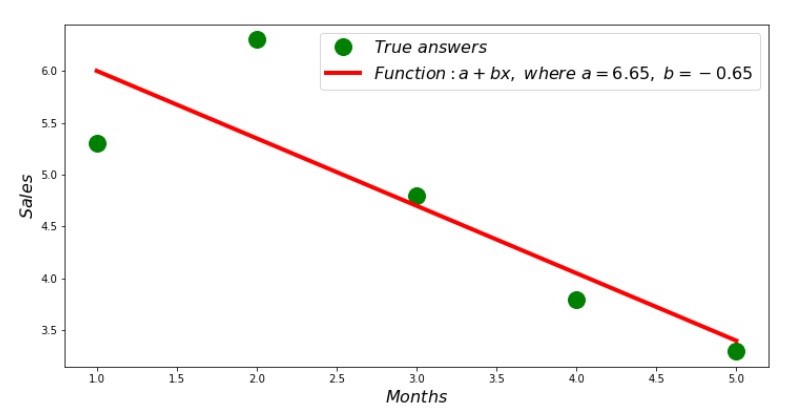



Anda dapat melihat jadwal deviasi untuk setiap bulan. Dalam kasus kami, kami tidak dapat mengambil nilai praktis yang signifikan darinya, tetapi kami akan memuaskan keingintahuan seberapa baik persamaan regresi linier sederhana mencirikan ketergantungan pendapatan pada bulan dalam setahun.


Jadwal No. 3 “Penyimpangan,%”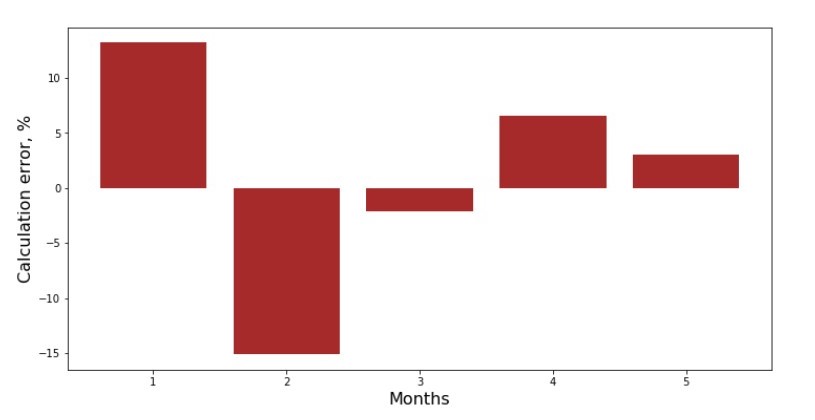



Tidak sempurna, tapi kami menyelesaikan tugas kami.

Kami menulis fungsi itu, untuk menentukan koefisien $$$a$ dan $$$b$ menggunakan perpustakaan NumPy , lebih tepatnya, kita akan menulis dua fungsi: satu menggunakan pseudo-inverse matrix (tidak direkomendasikan dalam praktiknya, karena prosesnya kompleks secara komputasional dan tidak stabil), yang lain menggunakan persamaan matriks.


Bandingkan waktu yang dibutuhkan untuk menentukan koefisien $$$a$ dan $$$b$ , sesuai dengan 3 metode yang disajikan.




Pada sejumlah kecil data, fungsi "tulis sendiri" muncul ke depan yang menemukan koefisien menggunakan metode Cramer.

Sekarang Anda dapat beralih ke cara lain untuk menemukan koefisien $$$a$ dan $$$b$ .

Keturunan gradien

Pertama, mari kita tentukan apa gradien itu. Secara sederhana, gradien adalah segmen yang menunjukkan arah pertumbuhan maksimum suatu fungsi. Dengan analogi dengan pendakian menanjak, di mana gradien terlihat, ada pendakian paling curam ke puncak gunung. Mengembangkan contoh gunung, kita ingat bahwa sebenarnya kita membutuhkan keturunan paling curam untuk mencapai dataran rendah sesegera mungkin, yaitu minimum - tempat di mana fungsi tidak bertambah atau berkurang. Pada titik ini, turunannya akan menjadi nol. Oleh karena itu, kita tidak perlu gradien, tetapi anti-gradien. Untuk menemukan anti-gradien, Anda hanya perlu mengalikan gradien dengan -1 (minus satu).

Kami menarik perhatian pada fakta bahwa suatu fungsi dapat memiliki beberapa minimum, dan setelah turun ke salah satu dari mereka sesuai dengan algoritma yang diusulkan di bawah ini, kami tidak akan dapat menemukan minimum lain yang mungkin lebih rendah dari yang ditemukan. Tenang, kita tidak dalam bahaya! Dalam kasus kami, kami berhadapan dengan satu minimum, karena fungsi kami $$$\ jumlah \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ pada grafik adalah parabola biasa. Dan seperti yang kita semua harus ketahui dengan baik dari pelajaran matematika di sekolah, parabola hanya memiliki satu minimum.

Setelah kami mengetahui mengapa kami membutuhkan gradien, dan juga bahwa gradien adalah segmen, yaitu, vektor dengan koordinat yang diberikan, yang merupakan koefisien yang persis sama $$$a$ dan $$$b$ kita bisa menerapkan gradient descent.

Sebelum memulai, saya sarankan membaca hanya beberapa kalimat tentang algoritma penurunan:

• Kami menentukan koordinat koefisien dengan cara pseudo-acak $$$a$ dan $$$b$ . Dalam contoh kita, kita akan menentukan koefisien mendekati nol. Ini adalah praktik umum, tetapi setiap praktik mungkin memiliki praktiknya sendiri.
• Dari koordinat $$$a$ kurangi nilai turunan parsial orde 1 di titik $$$a$ . Jadi, jika turunannya positif, maka fungsinya meningkat. Oleh karena itu, dengan menghilangkan nilai turunannya, kita akan bergerak ke arah pertumbuhan yang berlawanan, yaitu ke arah penurunan. Jika turunannya negatif, maka fungsi pada titik ini menurun dan menghilangkan nilai turunannya, kita bergerak menuju keturunan.
• Kami melakukan operasi serupa dengan koordinat $$$b$ : kurangi nilai turunan parsial pada titik tersebut $$$b$ .
• Agar tidak melompat minimum dan tidak terbang ke ruang yang jauh, perlu untuk mengatur ukuran langkah menuju keturunan. Secara umum, Anda dapat menulis seluruh artikel tentang cara mengatur langkah dengan benar dan bagaimana mengubahnya selama penurunan untuk mengurangi biaya perhitungan. Tapi sekarang kami memiliki tugas yang sedikit berbeda, dan kami akan menetapkan ukuran langkah dengan metode ilmiah "menusuk" atau, seperti yang mereka katakan pada orang biasa, secara empiris.
• Setelah kita dari koordinat yang diberikan $$$a$ dan $$$b$ dikurangi nilai derivatif, kami mendapatkan koordinat baru $$$a$ dan $$$b$ . Kami mengambil langkah berikutnya (pengurangan), sudah dari koordinat yang dihitung. Maka siklus dimulai lagi dan lagi, sampai konvergensi yang diperlukan tercapai.

Itu saja! Sekarang kita siap untuk mencari ngarai terdalam dari Palung Mariana. Turun.




Kami terjun ke bagian paling bawah Palung Mariana dan di sana kami menemukan semua nilai koefisien yang sama $$$a$ dan $$$b$ , yang sebenarnya diharapkan.

Mari kita selami lagi, hanya saja kali ini, pengisian kendaraan laut dalam kita akan menjadi teknologi lain, yaitu perpustakaan NumPy .



Nilai Koefisien $$$a$ dan $$$b$ tidak berubah.

Mari kita lihat bagaimana kesalahan berubah selama gradient descent, yaitu, bagaimana jumlah deviasi kuadrat berubah dengan setiap langkah.


Bagan №4 “Jumlah kuadrat penyimpangan dalam gradient descent”



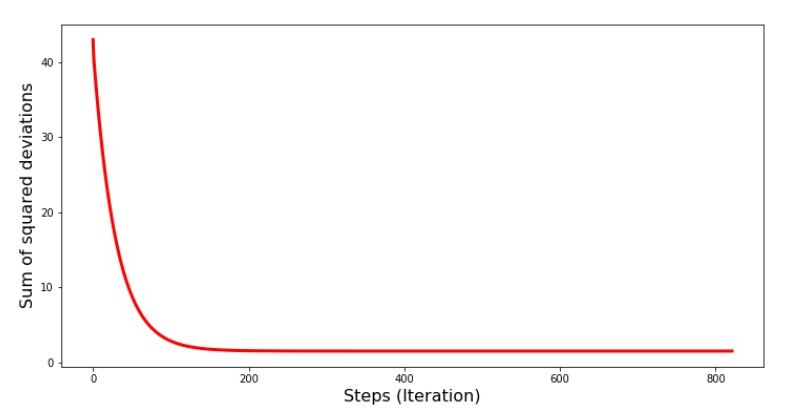
Pada grafik kita melihat bahwa dengan setiap langkah kesalahan berkurang, dan setelah sejumlah iterasi kita mengamati garis horizontal praktis.

Akhirnya, kami memperkirakan perbedaan waktu eksekusi kode:




Mungkin kita melakukan sesuatu yang salah, tetapi sekali lagi, fungsi "tulis-sendiri" sederhana yang tidak menggunakan perpustakaan NumPy lebih dulu menggunakan fungsi menggunakan perpustakaan NumPy .

Tetapi kita tidak diam, tetapi bergerak menuju studi tentang cara menarik lain untuk menyelesaikan persamaan regresi linier sederhana. Temui aku!

Penurunan gradien stokastik

Untuk dapat dengan cepat memahami prinsip operasi penurunan gradien stokastik, lebih baik untuk menentukan perbedaannya dari penurunan gradien biasa. Kami, dalam kasus gradient descent, dalam persamaan turunan dari $$$a$ dan $$$a$ menggunakan jumlah nilai semua atribut dan jawaban sebenarnya yang tersedia dalam sampel (mis., jumlah semua $$$x_i$ dan $$$y_i$ ) Dalam penurunan gradien stokastik, kami tidak akan menggunakan semua nilai yang tersedia dalam sampel, tetapi sebaliknya, secara pseudo-acak, kami akan memilih apa yang disebut indeks sampel dan menggunakan nilainya.

Misalnya, jika indeks ditentukan oleh angka 3 (tiga), maka kita ambil nilainya $$$x_3 = 3$ dan $$$y_3 = $ 4,$ , lalu kami mengganti nilai dalam persamaan derivatif dan menentukan koordinat baru. Kemudian, setelah menentukan koordinat, kami lagi pseudo-acak menentukan indeks sampel, mengganti nilai yang sesuai dengan indeks dalam persamaan diferensial parsial, dan menentukan koordinat dengan cara baru $$$a$ dan $$$a$ dll. sebelum penghijauan konvergensi. Sekilas, sepertinya ini bisa berhasil, tetapi berhasil. Benar, perlu dicatat bahwa tidak setiap langkah mengurangi kesalahan, tetapi trennya pasti ada.

Apa kelebihan dari penurunan gradien stokastik dari biasanya? Jika ukuran sampel kami sangat besar dan diukur dalam puluhan ribu nilai, maka itu jauh lebih mudah untuk diproses, katakanlah ribuan acak dari mereka daripada seluruh sampel. Dalam hal ini, penurunan gradien stokastik diluncurkan. Dalam kasus kami, tentu saja, kami tidak akan melihat perbedaan besar.

Kami melihat kodenya.




Kami melihat dengan hati-hati pada koefisien dan menangkap pertanyaan "Bagaimana bisa begitu?". Kami mendapat nilai lain dari koefisien $$$a$ dan $$$b$ . Mungkin penurunan gradien stokastik menemukan parameter persamaan yang lebih optimal? Sayangnya, tidak. Cukup untuk melihat jumlah dari penyimpangan kuadrat dan melihat bahwa dengan nilai-nilai baru dari koefisien, kesalahan lebih besar. Jangan terburu-buru putus asa. Kami merencanakan perubahan kesalahan.


Bagan №5 “Jumlah kuadrat penyimpangan dalam penurunan gradien stokastik”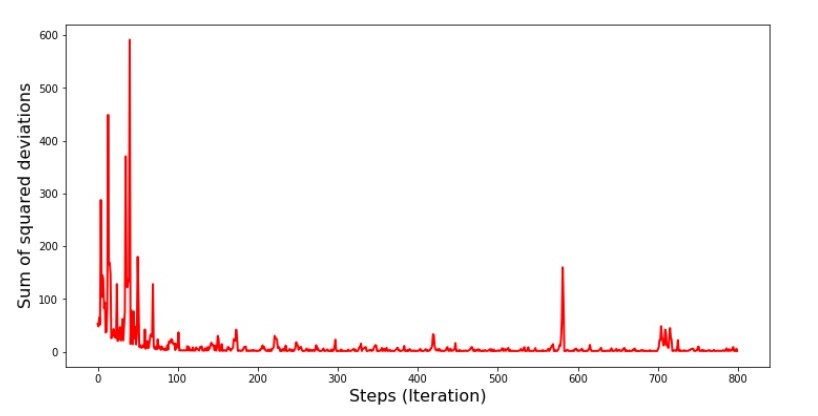



Setelah melihat jadwal, semuanya jatuh ke tempatnya dan sekarang kami akan memperbaiki semuanya.

Jadi apa yang terjadi? Berikut ini terjadi.Ketika kami memilih secara acak satu bulan, untuk bulan yang dipilih itulah algoritma kami berupaya mengurangi kesalahan dalam menghitung pendapatan. Kemudian kami memilih bulan lain dan mengulangi perhitungan, tetapi kami telah mengurangi kesalahan untuk bulan kedua yang dipilih. Dan sekarang mari kita ingat bahwa selama dua bulan pertama kita telah secara signifikan menyimpang dari garis persamaan regresi linier sederhana. Ini berarti bahwa ketika salah satu dari dua bulan ini dipilih, kemudian mengurangi kesalahan masing-masing, algoritma kami secara serius meningkatkan kesalahan di seluruh sampel. Jadi apa yang harus dilakukan? Jawabannya sederhana: Anda perlu mengurangi langkah penurunan. Setelah semua, dengan mengurangi langkah keturunan, kesalahan juga akan berhenti "melompat" ke atas dan ke bawah. Sebaliknya, kesalahan "lewati" tidak akan berhenti, tetapi tidak akan melakukannya dengan sangat cepat :) Kami akan memeriksa.




Bagan №6 “Jumlah penyimpangan kuadrat dalam penurunan gradien stokastik (80 ribu langkah)”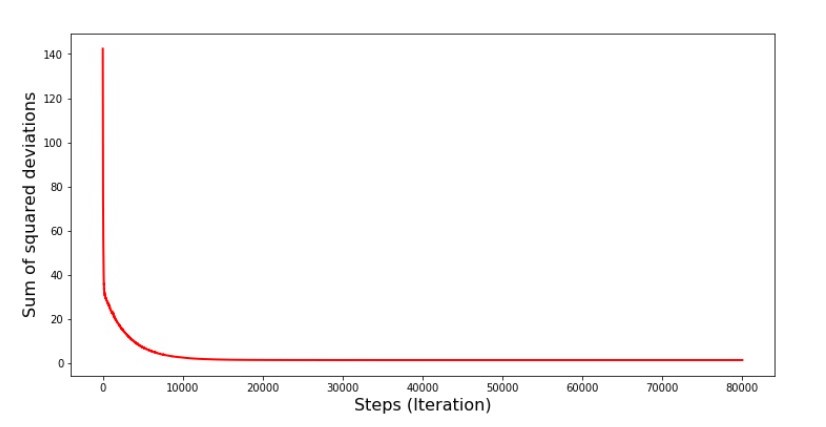



Nilai-nilai koefisien meningkat, tetapi masih belum ideal. Secara hipotesis, ini dapat diperbaiki dengan cara ini. Misalnya, pada 1000 iterasi terakhir, kami memilih nilai-nilai koefisien dengan kesalahan minimal yang dibuat. Benar, untuk ini kita harus menuliskan nilai koefisien sendiri. Kami tidak akan melakukan ini, melainkan memperhatikan jadwal. Terlihat mulus, dan kesalahannya tampak berkurang secara merata. Ini sebenarnya tidak demikian. Mari kita lihat 1000 iterasi pertama dan membandingkannya dengan yang terakhir.


Jadwal No. 7 "Jumlah kuadrat dari penyimpangan SGD (1000 langkah pertama)"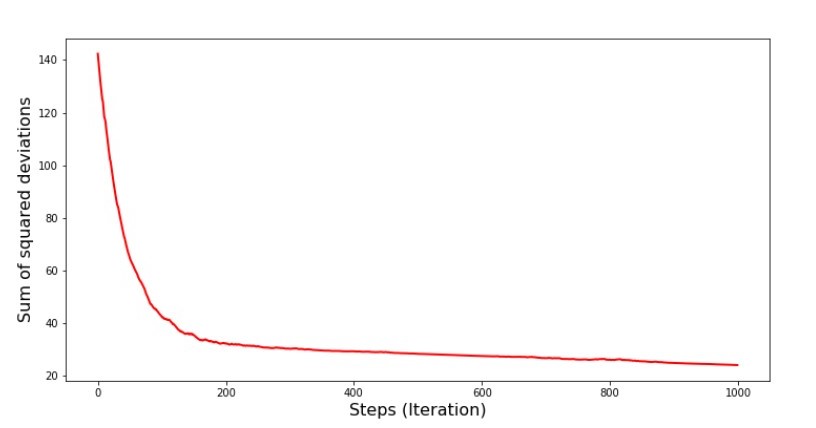



Grafik No. 8 "Jumlah kuadrat dari penyimpangan SGD (1000 langkah terakhir)"



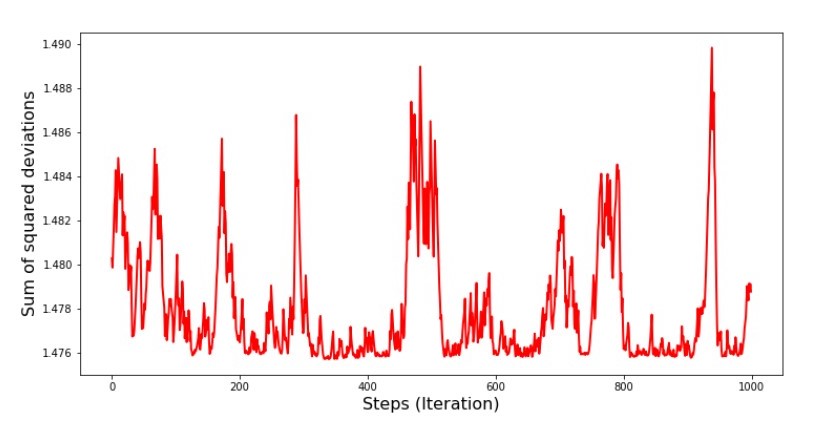Pada awal keturunan kita mengamati penurunan kesalahan yang cukup seragam dan tajam. Pada iterasi terakhir, kita melihat bahwa kesalahan berjalan di sekitar dan sekitar nilai 1,475 dan pada beberapa titik bahkan sama dengan nilai optimal ini, tetapi kemudian naik ke atas pula ... Sekali lagi, saya dapat menulis nilai-nilai koefisien$$$a$ dan $$b , lalu pilih yang kesalahannya minimal. Namun, kami memiliki masalah yang lebih serius: kami harus mengambil 80 ribu langkah (lihat kode) untuk mendapatkan nilai mendekati optimal. Dan ini sudah bertentangan dengan ide penghematan waktu komputasi dengan penurunan gradien stokastik relatif terhadap gradien. Apa yang bisa diperbaiki dan diperbaiki? Tidak sulit untuk memperhatikan bahwa pada iterasi pertama kita dengan percaya diri turun dan, oleh karena itu, kita harus meninggalkan langkah besar di iterasi pertama dan mengurangi langkah saat kita bergerak maju. Kami tidak akan melakukan ini di artikel ini - itu sudah diseret. Mereka yang berharap dapat berpikir bagaimana melakukan ini, itu tidak sulit :)Sekarang kita akan melakukan penurunan gradien stokastik menggunakan perpustakaanNumPy$b$

(dan kami tidak akan tersandung batu yang kami identifikasi sebelumnya)




Nilai ternyata hampir sama dengan saat turun tanpa menggunakan NumPy . Namun, ini logis.

Kita akan mengetahui berapa banyak waktu yang diambil oleh gradien stokastik gradien.




Semakin jauh ke dalam hutan, semakin gelap awan: lagi-lagi rumus "tulis sendiri" menunjukkan hasil terbaik. Semua ini menunjukkan bahwa harus ada cara yang bahkan lebih halus untuk menggunakan perpustakaan NumPy , yang benar-benar mempercepat operasi perhitungan. Pada artikel ini kita tidak akan mengetahuinya. Akan ada sesuatu untuk dipikirkan di waktu luang Anda :)

Ringkaslah

Sebelum merangkum, saya ingin menjawab pertanyaan yang kemungkinan besar muncul dari pembaca yang kami kasihi. Mengapa, pada kenyataannya, “siksaan” semacam itu dengan keturunan, mengapa kita harus naik dan turun gunung (terutama turun) untuk menemukan dataran rendah yang berharga, jika kita memiliki alat yang begitu kuat dan sederhana di tangan kita, dalam bentuk solusi analitis yang secara instan mengirim kita ke tempat yang tepat?

Jawaban atas pertanyaan ini terletak di permukaan. Sekarang kita telah memeriksa contoh yang sangat sederhana di mana jawaban yang benar$$y i tergantung pada satu atribut$y_i$$$$x_i$ .Dalam kehidupan, ini tidak sering terlihat, jadi bayangkan bahwa kita memiliki tanda-tanda 2, 30, 50 atau lebih. Tambahkan ke ribuan ini, atau bahkan puluhan ribu nilai untuk setiap atribut. Dalam hal ini, solusi analitis mungkin tidak lulus tes dan gagal. Pada gilirannya, gradient descent dan variasinya akan perlahan tapi pasti membawa kita lebih dekat ke tujuan - minimum fungsi. Dan jangan khawatir tentang kecepatan - kami mungkin juga akan menganalisis metode yang akan memungkinkan kami untuk mengatur dan menyesuaikan panjang langkah (mis. Kecepatan).

Dan sekarang sebenarnya ringkasan singkat.

Pertama, saya berharap bahwa materi yang disajikan dalam artikel ini akan membantu pemula "berkencan dengan Ilmuwan" dalam memahami bagaimana menyelesaikan persamaan regresi linier sederhana (dan tidak hanya).

Kedua, kami memeriksa beberapa cara untuk menyelesaikan persamaan. Sekarang, tergantung pada situasinya, kita dapat memilih salah satu yang paling cocok untuk menyelesaikan masalah.

Ketiga, kami melihat kekuatan pengaturan tambahan, yaitu panjang langkah dari gradient descent. Parameter ini tidak dapat diabaikan. Seperti disebutkan di atas, untuk mengurangi biaya perhitungan, panjang langkah harus diubah sepanjang keturunan.

Keempat, dalam kasus kami, fungsi "menulis sendiri" menunjukkan hasil temporal terbaik. Ini mungkin karena bukan penggunaan yang paling profesional dari kemampuan perpustakaan NumPy. Namun demikian, kesimpulannya adalah sebagai berikut. Di satu sisi, kadang-kadang ada baiknya mempertanyakan pendapat yang sudah mapan, dan di sisi lain, tidak selalu layak mempersulit hal - sebaliknya, kadang-kadang cara yang lebih sederhana untuk menyelesaikan masalah lebih efektif. Dan karena tujuan kami adalah untuk menganalisis tiga pendekatan dalam menyelesaikan persamaan regresi linier sederhana, penggunaan fungsi "menulis sendiri" sudah cukup bagi kami.

← Karya sebelumnya dari penulis - “Kami mempelajari pernyataan teorema limit pusat menggunakan distribusi eksponensial”$\leftarrow$
→ Karya selanjutnya dari penulis - “Kami membawa persamaan regresi linier ke dalam bentuk matriks”$\rightarrow$

Sastra (atau sesuatu seperti itu)

1. Regresi linier

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. Metoda kuadrat terkecil

mathprofi.ru/metod_naimenshih_kvadratov.html

3. Derivatif

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4.

Matematika Gradien /proizvodnaja_po_napravleniju_i_gradient.html

5. Gradient descent

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com//2017-12-31/linear_regressive

6. NumPy library

docs.scipy.org/doc/ numpy-1.10.1 / referensi / dihasilkan / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. html