Kami memeriksa metode Monte Carlo , hari ini kita akan melihat bagaimana otak komputer bermain pada tahun 2048 menggunakan minimax tua yang bagus dengan kliping alpha-beta.

Artikel itu ditulis dengan dukungan EDISON, sebuah perusahaan yang mengembangkan aplikasi seluler dan menyediakan layanan pengujian perangkat lunak .
Solusi dimata-matai oleh pengguna stackoverflow
 ovolve
ovolve , yang mencatat dalam diskusi
cara mengajar AI game 2048 .
Terjemahan terjemahan dari ovolveSaya penulis program yang disebutkan dalam utas ini. Anda dapat melihat AI
sedang beraksi atau melihat
kode .
Saat ini, program ini menang di sekitar 90% kasus dengan mengeksekusi skrip java di browser di laptop saya, menghabiskan 100 milidetik untuk memikirkan kursus, bekerja, meskipun tidak sempurna, tetapi cukup baik.
Karena gim ini adalah ruang keadaan diskrit dengan informasi lengkap, bahkan menjadi gim berbasis giliran seperti catur dan catur, saya menggunakan metode yang sama yang menunjukkan kinerja mereka dalam gim-gim ini, yaitu
pencarian minimax dengan
kliping alpha-beta . Karena tautan memberikan banyak informasi tentang algoritme ini, saya hanya akan berbicara tentang dua heuristik utama yang saya gunakan dalam
fungsi estimasi statis dan memformalkan banyak asumsi intuitif yang dibuat oleh orang lain di sini.

Monoton
Heuristik ini mencoba untuk memastikan bahwa semua nilai petak naik atau turun baik kiri / kanan dan atas / bawah. Heuristik ini sendiri mencerminkan dugaan yang telah disebutkan oleh banyak orang lain bahwa ubin yang lebih berharga harus dikelompokkan di sudut. Ini, sebagai suatu peraturan, mencegah akumulasi ubin yang kurang berharga dan membuat papan tetap teratur, karena ubin yang lebih kecil mengalir menjadi yang lebih besar.
Berikut adalah tangkapan layar dari kotak yang sepenuhnya monoton. Saya mendapatkan situasi ini dengan menjalankan algoritme dengan fungsi eval yang terinstal untuk mengabaikan heuristik lain dan hanya memperhitungkan monoton.

Smoothness (kehalusan, kemerataan)
Heuristik di atas dalam dirinya sendiri cenderung menciptakan struktur di mana sel-sel tetangga berkurang nilainya, namun, tentu saja, tetangga harus memiliki makna yang sama untuk digabungkan. Oleh karena itu, heuristic of smoothness hanya mengukur perbedaan nilai antara ubin yang berdekatan, mencoba untuk meminimalkan jumlahnya.
Seorang komentator di Hacker News memberikan
formalisasi yang menarik dari ide ini dalam hal teori grafik.
Terjemahan formalisasi dengan Hacker NewsKemarin saya menunjukkan game ini kepada seorang kolega, pecinta teori grafik, dan kami juga memutuskan untuk berpikir tentang bagaimana menyelesaikan game ini menggunakan AI.
Solusi paling sederhana adalah minimax, yang, seperti yang saya lihat, diimplementasikan dengan cukup baik. Jika seseorang di sini tidak terbiasa dengan minimax, OP menulis kode yang sangat elegan dan banyak komentar yang akan menjadi tutorial yang bagus.
Pendekatan yang kurang intensif secara komputasi yang kami usulkan adalah memodelkan kondisi permainan dalam bentuk grafik G (V, E) , di mana V adalah himpunan ubin aktif dan E adalah himpunan tepi yang menghubungkan ubin yang berdekatan yang dibebani oleh fungsi c (v1, v2) , yang mengembalikan nilai absolut dari perbedaan antara dua ubin. Untuk setiap solusi, AI memilih langkah yang meminimalkan jumlah bobot semua sisi dalam kondisi permainan baru.
Alasan untuk ini adalah bahwa satu-satunya cara untuk membuat kemajuan dalam permainan adalah memiliki ubin dengan nilai yang sama di samping satu sama lain, di mana bobot dalam G adalah 0. Dengan demikian, AI harus mencoba untuk meminimalkan total berat. Pada akhirnya, akan ada sejumlah besar di papan dengan berat tepi yang besar untuk ubin yang berdekatan, sehingga AI akan mencoba untuk menjaga ubin ini di sebelah ubin besar lainnya untuk meminimalkan perbedaan.
Karena permainan ini bersifat stokastik, pendekatan yang saya jelaskan mungkin tidak berfungsi dalam kasus terburuk, tetapi juga dapat diterapkan pada solusi minimax yang ada sebagai fungsi bobot untuk setiap simpul di pohon.
Ini adalah tangkapan layar dari jaring yang sangat halus, disediakan oleh
garpu mock yang luar biasa ini.
(tautan ke arsip web, sementara skrip Java pada halaman berfungsi dan Anda dapat menggunakan keyboard untuk bergerak ke arah mana pun - perhatikan oleh penerjemah).Ubin longgar
Dan akhirnya, ada penalti karena terlalu sedikit ubin gratis, karena opsi dapat dengan cepat berakhir ketika lapangan bermain menjadi terlalu sempit.
Dan itu saja! Mencari ruang permainan sambil mengoptimalkan kriteria ini memberikan kinerja yang sangat baik. Salah satu manfaat menggunakan pendekatan generik seperti ini daripada strategi langkah yang dikodekan secara eksplisit adalah bahwa algoritma sering dapat menemukan solusi yang menarik dan tidak terduga. Jika Anda mengamati kemajuannya, ia sering membuat gerakan yang luar biasa tetapi efektif, seperti perubahan tiba-tiba dinding atau sudut, di dekat tempat ia membangun permainannya.

Perubahan kecil
Tangkapan layar menunjukkan kekuatan dari pendekatan ini. Saya menghapus batas ubin (sehingga mereka terus tumbuh setelah mencapai 2048), dan inilah hasil terbaik setelah delapan tes.
Ya, ini adalah 4096 bersama dengan 2048. =) Ini berarti bahwa ia telah mencapai ubin 2048 yang sulit dipahami pada satu papan.
Kode Java-Script untuk minimax dengan kliping alpha-beta dan fungsi evaluasi statis dari stackoverflow yang diberikan pengguna diberikan di bawah ini dalam artikel.
Metode minimax dikhususkan untuk beberapa artikel habr-sangat baik, jadi kami menghilangkan penjelasan rinci akademis dari apa itu terdiri. Bagi mereka yang
bergabung dengan komunitas TI baru-baru ini mendengar istilah indah "minimax" dan "alpha-beta cut-off," tetapi mereka tidak tahu apa artinya ini, mari kita coba, secara harfiah dalam beberapa paragraf, untuk menjelaskan arti paling umum.
Minimax
Dalam beberapa game, proses permainan antara dua pemain (yang bergerak pada gilirannya) dapat direpresentasikan sebagai pohon pilihan. Di setiap posisi tertentu, setiap pemain biasanya memiliki pilihan antara opsi yang berbeda untuk kepindahannya. Dan dalam menanggapi setiap opsi ini, lawan juga bisa seperti dalam banyak hal.
Fragmen pohon opsiKarena pada setiap saat permainan ada informasi lengkap tentang keadaan lapangan bermain, keadaan posisi saat ini selalu dapat diperkirakan secara akurat. Fungsi seperti ini disebut
fungsi evaluasi statis atau disingkat
SFO . Selain itu, semakin penting fungsi ini ketika mengevaluasi posisi tertentu, semakin menguntungkan posisi untuk satu pemain (sebut saja
pemain yang memaksimalkan ). Semakin kecil nilai numerik fungsi ini saat mengevaluasi suatu posisi, semakin menguntungkan posisi pemain kedua (sebut saja
pemain yang meminimalkan ).
Setelah setiap gerakan, posisi berubah, dan skornya berubah. Ketika mempertimbangkan pohon pilihan, setiap pemain harus tidak hanya memilih cabang-cabang di mana peringkat paling menguntungkan baginya. Anda juga harus menghindari cabang-cabang di mana evaluasi posisi menguntungkan bagi lawan.
Diasumsikan bahwa lawan juga dibimbing oleh rasionalisme dan juga menghindari pilihan yang bisa membuatnya kalah. Artinya, setiap pemain, ketika memilih opsi, hasil dari memaksimalkan keuntungannya sendiri dan pada saat yang sama meminimalkan keuntungan lawan.
Ini minimax.
Kliping alfa beta
Sangat jelas: siapa yang menghitung pohon dari posisi yang diberikan ke kedalaman yang lebih besar, ia memiliki lebih banyak peluang untuk menang. Tetapi ada satu gangguan - pohon pilihan dalam permainan memiliki kebiasaan buruk bercabang dan tumbuh secara eksponensial dengan setiap tingkat bersarang. Kemampuan menghitung program, dan terlebih lagi orang terbatas, menghitung "sampai ke matras" jauh dari selalu mungkin. Dapat dengan mudah berubah bahwa pemain telah menghitung ke posisi di mana ia memiliki penilaian yang baik dari lapangan bermain, tetapi secara harfiah pada tingkat berikutnya (tidak terbaca), lawan memiliki kesempatan untuk membuat gerakan seperti itu yang secara radikal mengubah estimasi posisi ke arah sebaliknya.
Siapa yang harus disalahkan dan apa yang harus dilakukan? Kompleksitas komputasi yang harus disalahkan untuk traversal pohon lengkap, diusulkan untuk bertarung dengan memotong cabang yang tidak perlu. Jika pemain mengevaluasi posisi melihat bahwa beberapa cabang dari pohon opsi:
atau kurang menguntungkan untuk itu daripada cabang lain yang telah dianalisis,
atau lebih menguntungkan lawan daripada cabang lain yang sudah dianalisis,
maka pemain membuang cabang ini, tidak membuang waktu dan sumber daya untuk mempertimbangkan sub-opsi dari cabang yang jelas lebih buruk ini baginya.
Ini memungkinkan Anda mengalokasikan lebih banyak sumber daya komputasi untuk menghitung cabang yang lebih menguntungkan ke kedalaman rendering yang lebih besar di pohon opsi. Dalam proses mengevaluasi lapangan bermain pada level yang berbeda dari pohon opsi, pemain beroperasi dengan dua koefisien yang berubah secara dinamis -
alfa (nilai SFD yang paling sedikit ditemui di cabang - yaitu lebih menguntungkan bagi pemain yang meminimalkan) dan
beta (nilai SFD yang paling banyak ditemui di cabang - yaitu. lebih menguntungkan untuk pemain memaksimalkan). Pada setiap level, membandingkan SFD dari posisi saat ini dengan koefisien
alfa dan
beta memungkinkan Anda untuk menyapu (tanpa menghitungnya sepenuhnya) cabang yang
kurang menguntungkan bagi pemain mengevaluasi posisi dan / atau
lebih menguntungkan bagi lawannya.
Ini adalah kliping alpha beta.
Fungsi minimax rekursif dengan kliping alpha beta
2048 dengan AI diimplementasikan sebagai aplikasi Excel dengan makro VBA, ini adalah bagaimana algoritma minimax dengan kliping alpha beta terlihat seperti dasar visual yang tercela. Libatkan kode dalam java-script function AI(grid) { this.grid = grid; }
Fungsi Evaluasi Statis
Karena pada setiap level di pohon pilihan Anda harus mengevaluasi lapangan permainan (untuk memutuskan pemain mana, posisi yang diperkirakan sebenarnya lebih menguntungkan), Anda perlu memutuskan dengan kriteria apa untuk membedakan posisi yang baik dari yang buruk.
Kami berasumsi bahwa pemain memaksimalkan adalah orang (atau AI) yang memutuskan mana dari 4 arah (atas, kiri, kanan, bawah) untuk memindahkan semua ubin. Pemain yang meminimalkan adalah subrutin yang berbahaya yang secara acak menghasilkan 2 atau 4 di tempat yang paling tidak pantas.
SFO dikompilasi dari sudut pandang pemain yang memaksimalkan. Semakin tinggi peringkat SFD untuk lapangan bermain, semakin baik posisi untuk "maksimalis". Semakin rendah - semakin menyenangkan posisi di papan tulis untuk "minimalis".
Dalam kasus 2048 - faktor apa yang dianggap menguntungkan bagi orang yang memindahkan ubin?
Monoton
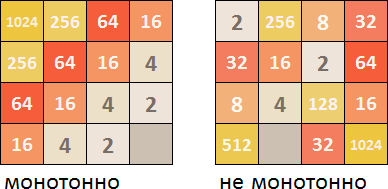
Pertama, diinginkan bahwa ubin disusun dalam urutan naik / turun di beberapa arah. Jika ini tidak dilakukan, maka ketika ubin baru dihasilkan, lapangan bermain akan dengan cepat tersumbat dengan ubin yang disusun secara acak dengan ukuran berbeda, yang tidak dapat langsung dihubungkan secara normal satu sama lain.
Di Distrik Federal Siberia, Anda perlu melihat semua 4 arah (top-down, kiri-ke-kanan, kanan-ke-kiri, bottom-up) dan menghitung di mana ubin adalah penurunan atau peningkatan perkembangan. Jika dalam perkembangan ada ubin yang tidak cocok dengan seri umum, maka ini mengurangi koefisien numerik monoton. Kemudian, dari 4 koefisien untuk semua arah, yang terbaik dipilih, yang diperhitungkan dalam nilai total Distrik Federal Siberia.
Kelancaran

Selain itu, akan lebih disukai jika perkembangan dari berdiri di barisan ubin tidak hanya meningkat, tetapi tidak menurun (atau bukannya menurun, lebih disukai daripada tidak meningkat), yaitu, itu baik ketika ubin yang sama di dekatnya, yang memungkinkan mereka untuk jatuh menjadi satu, mendapatkan poin dan meningkatkan ruang kosong di lapangan bermain.
Oleh karena itu, Distrik Federal Siberia sedang mencari ubin berdekatan yang sama di lapangan bermain dan memperhitungkan jumlah pasangan demikian dalam koefisien khusus.
Sel kosong

Jelas, semakin banyak ruang kosong, semakin banyak ruang untuk bermanuver dan semakin kecil kemungkinan untuk kalah.
SFO menganggap sel-sel kosong di lapangan dan semakin banyak, posisi ini dianggap lebih menguntungkan bagi pemain yang memaksimalkan.
Ubin maksimum
Karena hal utama dalam permainan ini adalah untuk mendapatkan ubin besar di lapangan, semakin banyak lebih baik - 2048, 4096, 8192 (atau apa pun yang Anda punya kekuatan dan kesabaran untuk), opsi di mana nilai ubin maksimum lebih harus dianggap sebagai SFD paling menguntungkan.
Distrik Federal Siberia untuk tahun 2048
Implementasi Distrik Federal Siberia sebagai makro VBA Libatkan kode dalam java-script function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
Aplikasi Excel itu sendiri
dapat diunduh dari Google .
Fungsi aplikasi dijelaskan
dalam artikel sebelumnya, di mana AI bermain menggunakan metode Monte Carlo . Solusi hari ini telah ditambahkan ke Monte Carlo yang ada.
Semua artikel seri AI dan 2048
- Monte Carlo
- Kliping minimumima + alpha beta
- Menunggu maksimum
- Jaringan saraf